单探测器型复合轴系统设计中的若干问题
2020-05-12杨松涛和丽清
杨松涛,和丽清
(中国电子科技集团公司第十一研究所,北京 100015)
1 引 言
随着光电对抗技术的不断发展,逐渐发展出装载于车载、舰载、机载和弹载等移动平台上的光电跟瞄系统。这些光电跟瞄系统不仅需要对目标进行高精度和持续的跟瞄,而且要求系统具备在载体运动条件下以及高振动和冲击等恶劣的工作环境下能够保持较高的激光指向精度,从而有效地通过激光能量实现对目标的干扰或破坏,最终完成对飞机和导弹等空中机动目标的干扰或杀伤[1-2]。
为了实现这些光电跟瞄系统对各种运动目标的高精度瞄准,复合轴控制技术应运而生,即在光电跟踪转台的激光发射光路中引进快速反射镜[3-9]。目前,复合轴控制技术已发展成为提高光电跟瞄系统跟瞄精度和带宽最行之有效的手段。
复合轴系统在工程中,一般分为单探测器型复合轴系统和双探测器型复合轴系统[10-14]。双探测器型复合轴系统首先通过粗跟踪控制回路将目标引入精探测器视场范围,然后精跟瞄回路补偿粗跟踪回路误差以实现高精度跟瞄,双探测器型复合轴系统现已获得广泛应用并取得了很好的跟瞄效果。单探测器复合轴系统在精度方面不如双探测器系统,但是单探测器型复合轴系统具有构成简单、装配难度低、功耗低、稳定性和可靠性高等优点,而且便于小型化,因此,单探测器型复合轴系统也有一定的应用领域。
但是,由于单探测器型复合轴系统采用一个探测器,因此其控制过程较为复杂且存在以下几方面问题:
(1)控制回路耦合问题:复合轴系统有两个控制回路,对于单探测型复合轴系统,主、子轴控制回路之间存在强烈的耦合。在实际系统设计中,需要通过设计去耦控制器,使单探测型复合轴系统成为静态自主系统,以使系统稳定。
(2)脱靶量计算问题:FSM的姿态角控制直接影响出射激光方向,决定着单探测器型复合轴系统总的激光指向精度。由于FSM采用45度反射镜结构安装在转台上,一般认为FSM补偿运动角度与探测器获得的脱靶量之间符合简单的2倍关系,但在单探测器型复合轴系统中,通过坐标变换推导可以证明两者之间不是简单的2倍关系问题。
(3)稳定补偿问题:激光光束控制装置在载体运动过程中,会因移动平台运动而使自身姿态发生改变,导致激光光束方向变化,从而影响激光的持续指向目标点。特别地,在单探测器型复合轴系统中,为满足主控制回路大视场角或者由于探测器原因(例如红外探测器等)致使系统无法获得高帧频的脱靶量信息。即使FSM控制回路实现了很高的控制精度和响应速度,也不能保证激光光束实时的指向同一位置。
2 单探测器型复合轴系统解耦原理
单探测器型复合轴系统的结构框图如图1所示。
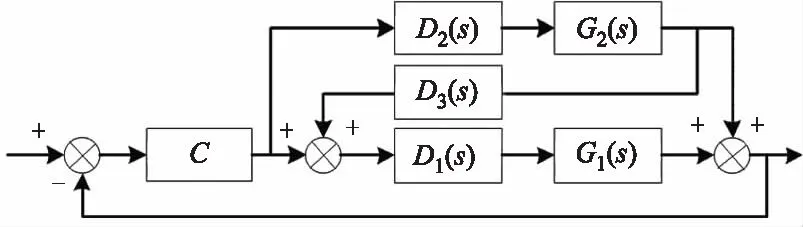
图1 单探测器型复合轴系统原理框图Fig.1 Principle diagram of single detector compound-axis servomechanism
根据图1可以得出单探测器型复合轴系统的传递函数为:
(1)
其中:C(s)、D3(s)、D1(s)、D2(s)、G1(s)和G2(s)分别为探测器、去耦控制器、主轴控制器、子轴控制器、主轴控制对象和子轴控制对象传递函数。
由式(1)可知,去耦控制器的特性D3(s)影响系统的稳定性,当D3(s)=C(s)时,系统才能成为静态自主系统,此时主、子系统稳定可保证单探测器型复合轴系统稳定。
由式(1)可得到,单探测器型复合轴系统的误差传递函数为:
E(s)=1-G(s)
(2)
由式(2)可知,当D3(s)=C(s)时,单探测器型复合轴系统的误差传递函数可以等效为主、子系统误差传递函数之积,这可以等效为系统的无差度为主、子系统无差度阶数之和,因此单探测器型复合轴系统可以提高转台的控制精度。
3 FSM脱靶量的解算原理
单探测器型复合轴系统的组成一般如图2所示,探测器成像系统与激光发射系统采用同轴但不共口径的方式。
当转台无跟踪误差时(探测器获得的脱靶量为0),FSM不需要偏转就能将激光光束准确的指向目标。但是,当转台存在跟踪误差时(探测器获得的脱靶量为:方位脱靶量Α和俯仰脱靶量Β,单位为rad),则需要FSM的两轴旋转角度(方位角为α和俯仰角为β)来修正转台误差。因此,FSM的存在可有效地提高激光光束指向精度。

图2 单探测器型复合轴系统组成Fig.2 The system of single detector compound-axis servomechanism
3.1 坐标系和坐标变换
首先建立框架坐标系OrXrYrZr,框架坐标系的原点规定为俯仰框架支承中心Or,探测器的视轴方向为OrXr轴正方向,YrOrZr平面与OrXr垂直,OrZr指向上,OrYr符合右手定律。由于FSM安装时与转台光轴存在45o夹角,则绕OrZr旋转α+45o可得到OrXr1Yr1Zr1坐标系,然后绕OrYr1旋转β可得到FSM坐标系OsXsYsZs,FSM坐标系的原点规定为FSM的旋转中心Os(假设Os与Or重合),FSM的法线方向为OsXs轴正方向,YsOsZs平面与OsXs垂直,OsZs指向上,OsYs符合右手定律。各坐标系之间的关系如图3所示。FSM坐标系与框架坐标系的变换关系可用以下的坐标旋转过程实现:
其中,α为FSM旋转的补偿方位角;β为FSM旋转的补偿俯仰角。

图3 坐标系之间的关系图Fig.3 The relation diagram of coordinates
则其变换矩阵可表示为:
(3)
3.2 推导FSM补偿角α、β和探测器脱靶量Α、Β之间的关系

(4)

(5)
由于FSM为反射镜,故P1点经过反射后的点(P2点)在FSM坐标系下坐标为:
(6)
又因为P2点在框架坐标系下的坐标为:
(7)
则通过式(4)和式(7)可建立等式方程,通过MATLAB符号工具箱可得到:
(8)
通过式(8)可以看出,FSM的控制输入角与转台误差角之间并不是简单的线性二分之一的关系,而是符合一个复杂的表达式。在系统要求较高的解算精度时,建议采用式(8)进行求解,但是在解算精度满足的条件下(方位脱靶量Α和俯仰脱靶量Β符合一定条件下),可以取其简化的表达式:
(9)
4 FSM的稳定补偿原理
激光光束控制系统在运行过程中会因载体的机动或外界各种扰动而使自身姿态发生改变,导致光束和视轴方向变化,从而影响激光光束的指向精度。即使在主跟踪框架安装了陀螺等惯性元件进行稳定控制的情况下,由于稳定控制误差的存在,也会发生激光光束在探测器获取两帧图像之间的时间内,出像激光光束偏离目标的现象。
由于FSM控制回路的带宽远远大于主跟踪框架控制回路的带宽,因此这个误差可以通过实时解算稳定误差导致光束偏离的角度,然后通过控制FSM旋转来进行补偿。通过这种方法得到的补偿可以使激光光束更好地对目标点进行持续和精准的照射。
假定探测器视场角为θy×θz,象素个数为Ny×Nz,则探测器视场角与象素的比例关系为:
(10)
假定探测器视场中心的坐标为(0,0),在拍照时刻t=0时获得的目标M的像素坐标记为(ym,zm)。在t>0时刻,探测器在滚转、俯仰、方位三个方向的旋转变化角记为ΔθR、ΔθP和ΔθH(由于载体相对惯性空间的运动产生)。目标在探测器视场内的移动变化如图4所示。
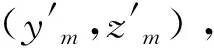
(11)



图4 载体姿态运动导致探测器运动时目标点的坐标变化Fig.4 The coordinate change of target caused by the motion error of the detector
当转台存在跟踪误差时,探测器获得的脱靶量为:方位脱靶量Α和俯仰脱靶量Β,则可得到:
(12)
则通过式(11)可得到图像两帧间的转台跟踪实时误差(载体相对惯性空间的运动产生的)的表达式:
(13)
其中:K=Ky/Kz。
通常,单探测器型复合轴系统的主跟踪框架都采用直接稳定两轴两框架结构,因此ΔθP和ΔθH可以通过对陀螺的实时俯仰角速度和方位角速度进行积分来获得,即:
(14)

对于ΔθR,可以通过两种方式获得:
(1)在内框架上安装一个滚转方向的陀螺,然后对陀螺的实时横滚角速度进行积分获得;
(2)运用安装在基座惯性设备里的陀螺,通过坐标变换推导获得探测器滚转方向的速度,然后对其进行积分获得。
在实际应用中,可以根据不同的要求和输入条件对式(13)进行近似处理。
如果ΔθR<0.045°时,可取sin(ΔθR)=ΔθR,cos(ΔθR)=1,则式(13)可以近似为:
(15)
实际应用时也可以去掉二次项:ΔθP·ΔθR/K和K·ΔθH·ΔθR。
如果系统中无法获得ΔθR,可取sin(ΔθR)=0,cos(ΔθR)=1,则式(13)可以近似为:
(16)
5 结 论
单探测器型复合轴系统在设计中存在控制回路耦合问题、脱靶量计算问题和稳定补偿问题,这些问题的存在可导致系统精度下降或者控制失败。本文通过对以上问题详细的理论分析和公式推导,得到了相应的理论表达式和计算公式。这些原理性的表达式和计算公式可使系统设计更有依据、控制输入更为精准。同时通过高精度的闭环控制,结合本文给出的处理方法可以实现高精度的单探测器型复合轴系统。
