低功耗高精度Sigma-Delta调制器的建模与设计

刘振宇, 宋树祥, 岑明灿, 蒋品群, 蔡超波

(广西师范大学 电子工程学院，广西 桂林 541004)

随着便携式可穿戴设备的飞速发展，高分辨率和低功耗语音芯片的需求持续增长，而Sigma-Delta调制器作为语音芯片主要部件，其设计的好坏直接决定了芯片的成败，因此设计一款高精度低功耗的调制器成为一项具有挑战性的任务。Sigma-Delta调制器主要分为CT(continuous-time)Sigma-Delta和DT(discrete-time)Sigma-Delta两类，由于环路滤波器结构上的差异，尽管CT调制器在带宽上表现优于DT调制器，但前者在实际电路中会引入非理想因素，在相同非理想因素的作用下DT调制器表现明显优于CT调制器[1-2]。

由于8 kHz带宽就能满足语音芯片Sigma-Delta调制器的应用需求，不需要1 MHz以上级别的大带宽，因此选用DT调制器更为合适。2011年Bonizzoni等[3]提出一种采用2个运算放大器设计三阶调制器的思想，但因其采用了5位量化技术，故会引入非线性，使调制器最终分辨率只有10 bits。2016年Kwon等[4]利用单环结构半延时积分技术实现了0.4 mW功耗下分辨率达13 bits的调制器，但是该技术对噪声整形滤波器性能要求苛刻不易于实现。2019年周志兴等[5]设计的调制器分辨率虽然达到了16 bits，但由于采用了传统的电路架构，其功耗高达4 mW。Sung等[6-7]于2017年实现了带宽可调的调制器，由于其采用了多位量化引入了非线性因素，造成该调制器分辨率仅有10 bits；2020年该团队采用四阶噪声整形2-2级联结构设计了一款分辨率达16 bits的调制器，但级联结构增加了电路的复杂度，使其功耗高达7.8 mW。2020年Li等[8]利用多位量化flash ADC技术和MASH架构设计了17.9 bits高分辨率的调制器，但由于引入了额外的ADC电路以及MASH架构，使得该调制器功耗高达68 mW。

针对上述问题，本文首先对传统架构的单环级联分布式前馈型调制器(cascade-of-integrators feed forward，CIFF)存在的不足进行分析，在第1章讲述系统级电路设计加入浮动系数迭代思想提升精度，第2.1节讲述晶体管级电路设计应用运放共享技术降低功耗。本文设计的调制器应用第1章提出的思想与第2.1节应用的技术相结合实现了预定的设计指标，以此满足语音芯片对低功耗、高精度Sigma-Delta调制器的需求。

1 Sigma-Delta调制器的系统级设计

调制器的有效位数大于或者等于16 bits可称为高分辨率，而Sigma-Delta调制器的高分辨率是依赖其过采样和噪声整形技术共同作用产生的效果。本文设计的Sigma-Delta调制器应用于语音芯片，分辨率需要达到16 bits，工作带宽8 kHz，采样频率4 MHz，过采样率256。下面将围绕上述指标对调制器各部分的设计进行分析。

调制器分辨率主要由调制器的量化器位数(B)、过采样率(OOSR)、噪声整形滤波器阶数(N)共同决定。信号量化噪声比(SSQNR)是衡量Sigma-Delta调制器分辨率的重要指标，其可以表示为[9]

(1)

由式(1)可知，通过提高量化器位数、过采样率、噪声整形滤波器阶数可使调制器实现较高的分辨率，但提高量化器位数会引入电路非线性问题，采用1 bit量化则可以避免出现此问题；过采样率越大，相应噪声整形滤波器需要的带宽就会越高，从而造成功耗增加，不符合设计低功耗调制器的理念；而增加滤波器的阶数会使得电路更加复杂、芯片面积占用过大，对器件的匹配性难度增加。基于上述因素，结合本文涉及调制器的应用场景折衷考虑，决定采用2阶1 bit单环CIFF型结构，过采样率OOSR取值256。

根据应用最广泛的Lee判据(Lee criterion)可知，一个量化位数为1 bit的Sigma-Delta调制器其经验稳定条件是噪声传递函数满足max|NTF(ejw)|<1.5[10]。因此在MATLAB建立Sigma-Delta调制器模型，如图1所示，其参数变量H设置小于1.5。

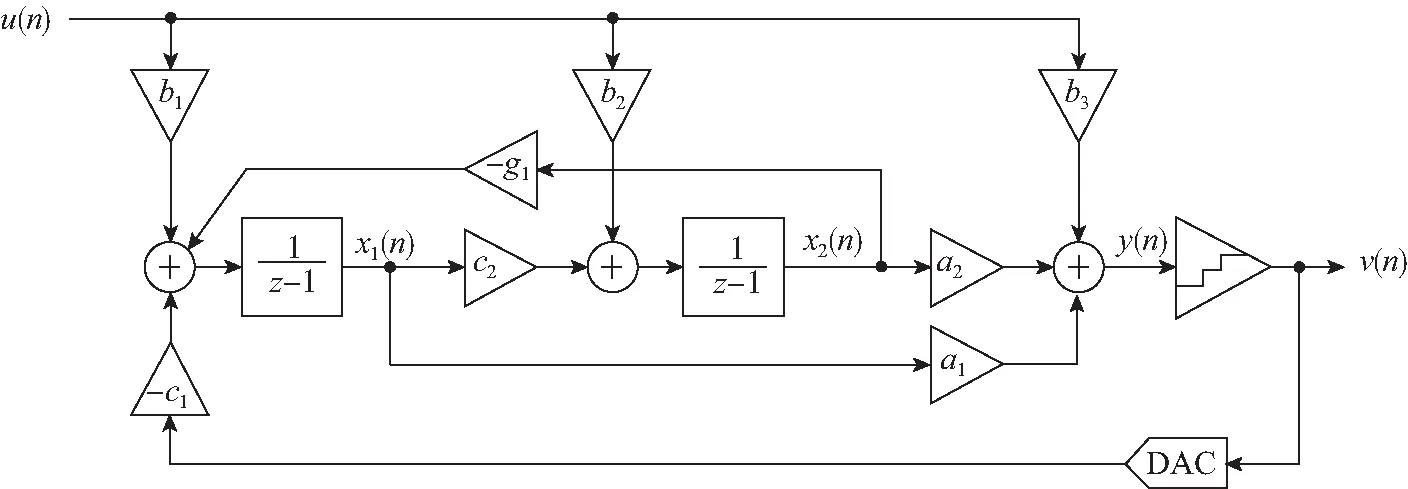
图1 MATLAB 2阶 CIFF SDM Simulink理论模型Fig. 1 Theoretical model of MATLAB second-order CIFF SDM Simulink

根据图1可得式(2)～(5)。变量u代表输入信号x(n)，变量v代表输出信号v(n)；变量x1代表图1中第1个积分器的输出x1(n)，变量x2代表图1中第2个积分器的输出x2(n)；y(n)为第3个积分器与各求和支路运算后的结果；变量a1、a2为反馈系数；变量b1、b2和b3为输入前馈系数；c1、c2为积分增益系数；g1为反馈系数；H为噪声传输函数设定的参数变量。

x1=(b1u-c1v-g1x2)H，

(2)

x2=(c2x1+b2u)H，

(3)

y=b3u+a2x2+a1x1，

(4)

v=y+e。

(5)

Sigma-Delta调制器的信号传输函数SSTF和噪声传递函数NNTF由式(2)～(5)联立可得：

(6)

(7)

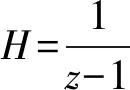
(8)

由式(1)至式(8)可得到本文调制器的各项系数，如表1所示。

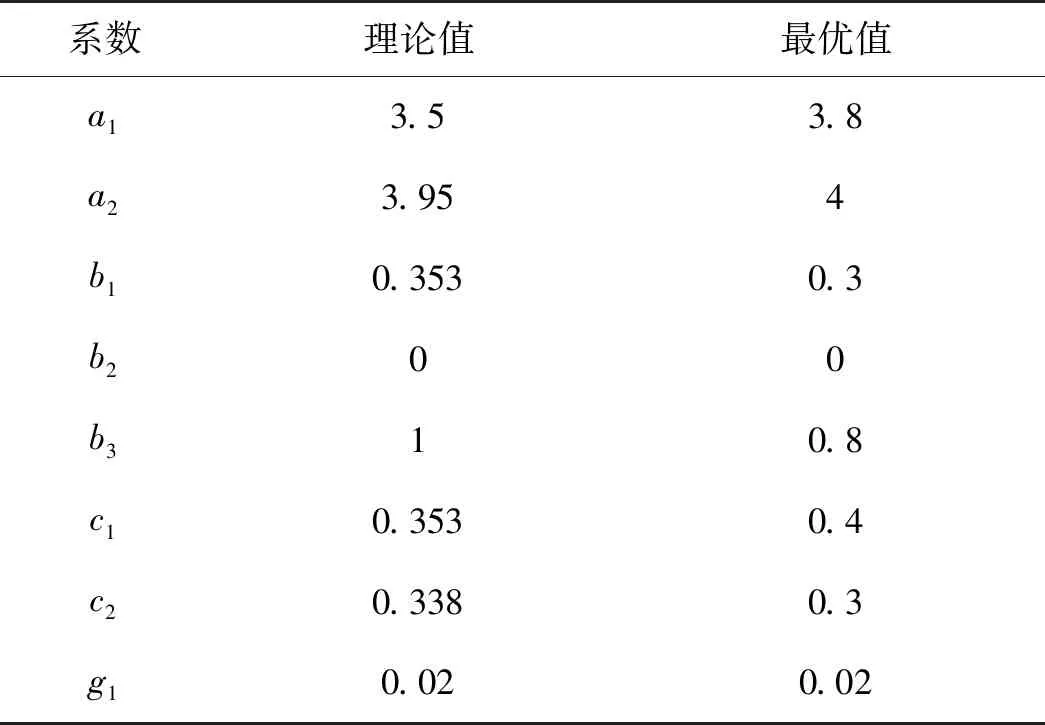
表1 Sigma-Delta调制器的系数理论值

传统的调制器建模方法通常通过传递函数求解出系数，如表1所示，再运用于MATLAB的Simulink模型中进行仿真验证。在开关电容电路中，由于电容值无法完全匹配，所以支路系数的取值无法完全和理论值相同。因此在实际情况中，电路的各项系数都会有一个抖动，要求设计出系统能够满足性能指标要求的最大抖动系数，即抖动门限抖动的大小取决于电路设计的精度。因此直接采用表1的系数理论值并不能使调制器的性能发挥到最佳。

为解决上述问题，本文将浮动系数迭代思想应用于传递函数中计算各个系数值。当各个模块子电路的匹配精度达到10%才能保证整个调制器相对稳定的精度[11-14]，因此本文提出的浮动系数迭代的浮动值定为各个系数的±10%。系统及设计中应用提出的浮动系数迭代思想运算的流程如图2所示。

利用上述思想将式(6)～(8)的参数分别设置±10%的波动后，利用MATLAB 的Simulink模型(如图3所示)进行迭代仿真，绘制出各个参数对整个调制器系统SNR的影响曲线，并根据曲线确定每个参数的最优值。以表1的系数a1理论值为例，利用迭代算法得到的浮动取值与SNR关系的曲线如图4所示。图4中，红色和蓝色的点分别代表a1取相应点对应横坐标数值时得到的最终输出SNR和DR，拟选取的数值点左右两侧数值点对应纵坐标值不能有太大的波动，否则将影响系统的问题定性。实竖线穿过的点代表a1最终取值。

图2 应用提出的浮动系数迭代思想运算的流程Fig. 2 Applying the proposed floating coefficient iteration idea to test the flow chart

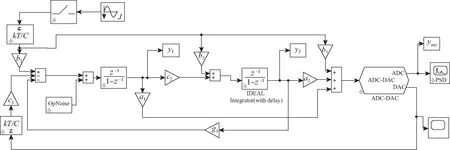
图3 2阶CIFF Sigma-Delta调制器MATLAB SIMULINK模型Fig. 3 MATLAB second-order CIFF SDM SIMULINK model

图4 以a1为例使用迭代算法得到的参数最优值Fig. 4 Taking a1 as an example, the optimal value of the parameter was obtained by using the iterative algorithm

图5(a)为表1系数理论值的输出频谱，图5(b)为表1系数最优值的输出频谱。从图5中可以清晰看到，最优值得到的SNR明显优于理论值得到的SNR，有效位数ENOB也比未进行系数迭代的高0.27 bit。

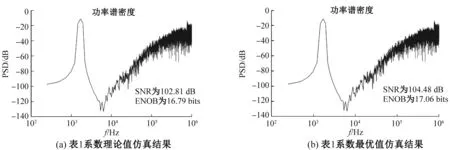
图5 不同系数的仿真结果Fig. 5 Simulation results of different coefficients

由文献[15]知，第一级采样电容可以通过式(9)确定，

(9)

根据预定指标有效位数EENOB=16 bits，SSNR≈1010，OOSR=256，VP=1 V，由式(9)得CS1=1.6 pF。

2 Sigma-Delta调制器晶体管级电路的实现

本文提出的基于浮动系数迭代思想的运放共享改进型低功耗高精度CIFF Sigma-Delta调制器如图6所示，该调制器包括由积分器构成的噪声整形滤波器、比较器、加法器和时钟产生电路。由于Sigma-Delta调制器的分辨率主要受第一级噪声整形滤波器的影响[16]，且本文采用的滤波器阶数为2阶，为达到低功耗条件下不降低精度，对如图7所示2阶传统结构的运放进行改进，将传统2阶结构的2个运放合并为一个运放，通过两相不交叠时钟控制其工作过程，可以消除第二级噪声整形滤波器引入的功耗[17-18]。

2.1 运放共享技术的分析与实现

由于图7中传统架构结构上下对称，故本文此处仅对Sigma-Delta调制器上半部分进行工作状态分析，如图8所示。图8(a)为调制器电路进行采样操作,图8(b)为调制器电路进行积分操作。

在图8中，粗线代表调制器该支路目前正在进行信号传输，VCM为电路的共模电压，用箭头指明相应状态下的信号传输方向。φ1相位，如图8(a)所示，第一级采样电容Cs1和第二级采样电容Cs2分别同时对输入信号Vi1和第一级积分器X1上一时刻输出的积分结果进行采样。φ2相位，如图8(b)所示，积分器X1、X2进行积分操作，积累在采样电容Cs1、Cs2上的电荷分别通过积分器X1、X2转移到积分电容Cf1、Cf2中。

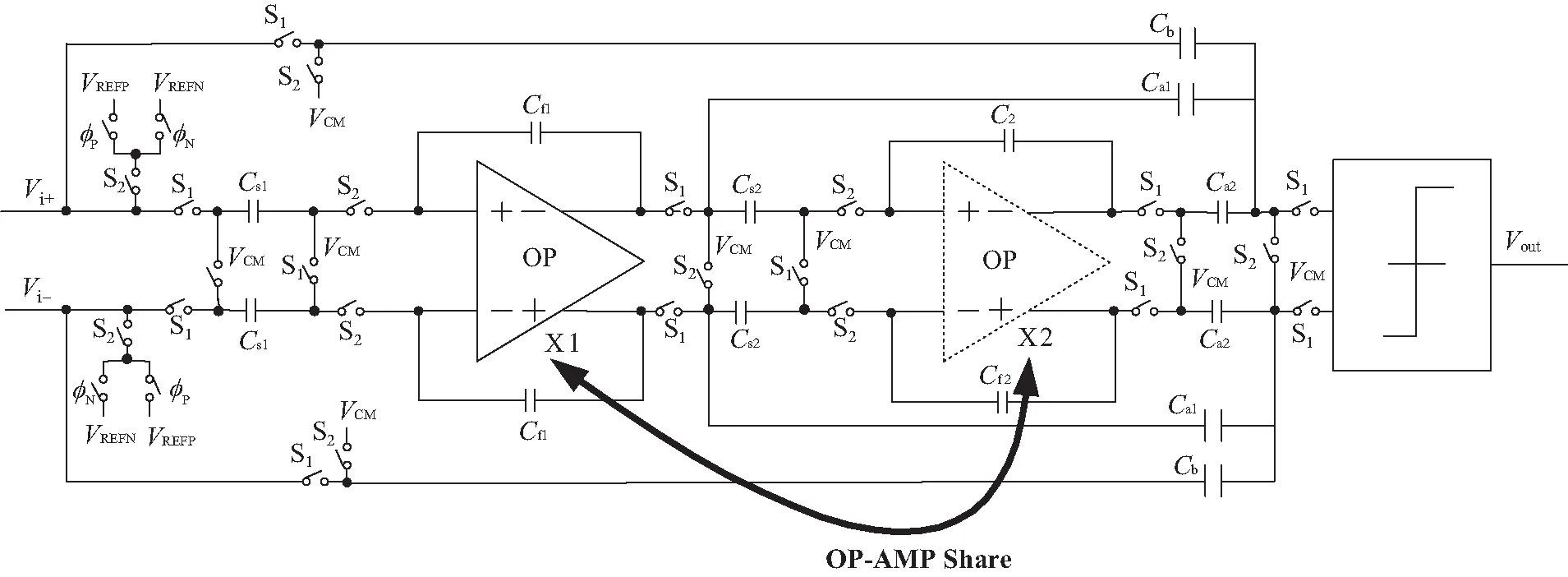
图6 改进型低功耗高精度CIFF Sigma-Delta调制器原理Fig. 6 Schematic diagram of improved CIFF sigma-delta modulator with low-power consumption and high-precision

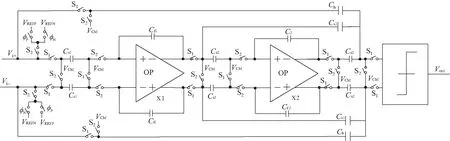
图7 传统2阶CIFF Sigma-Delta调制器结构原理Fig. 7 Schematic diagram of traditional 2rd CIFF sigma-delta modulator

图8的工作方式在每一个相位积分器只进行一个操作，但是却要引入2个积分器带来的功耗。为了解决该问题，本文提出2阶调制器只使用一个积分器，通过合理调整开关的顺序，做到积分器在同一个相位既能采样又可积分，具体电路原理如图9所示。分析图9结构时可以分为内环和外环2个部分：内环部分由开关S2、开关S1和采样电容Cs1、积分电容Cf1构成。从输入信号Vi1的输入开始，经开关S2、采样电容Cs1完成图8(a)传统结构中输入信号Vi1到采样电容Cs1的采样过程；通过开关S1、内环的积分电容Cf1和积分器X，完成图8(b)传统结构中第一级积分器的积分功能。外环由开关S2、开关S1和采样电容Cs2、积分电容Cf2构成。从图9中的积分器X输出Vop1out开始，经开关S1、采样电容Cs2完成图8(a)传统结构中第一级积分器输出到采样电容Cs2的采样过程；通过开关S2、外环的积分电容Cf2和积分器X，完成图8(b)传统结构中第二级积分器的积分功能。

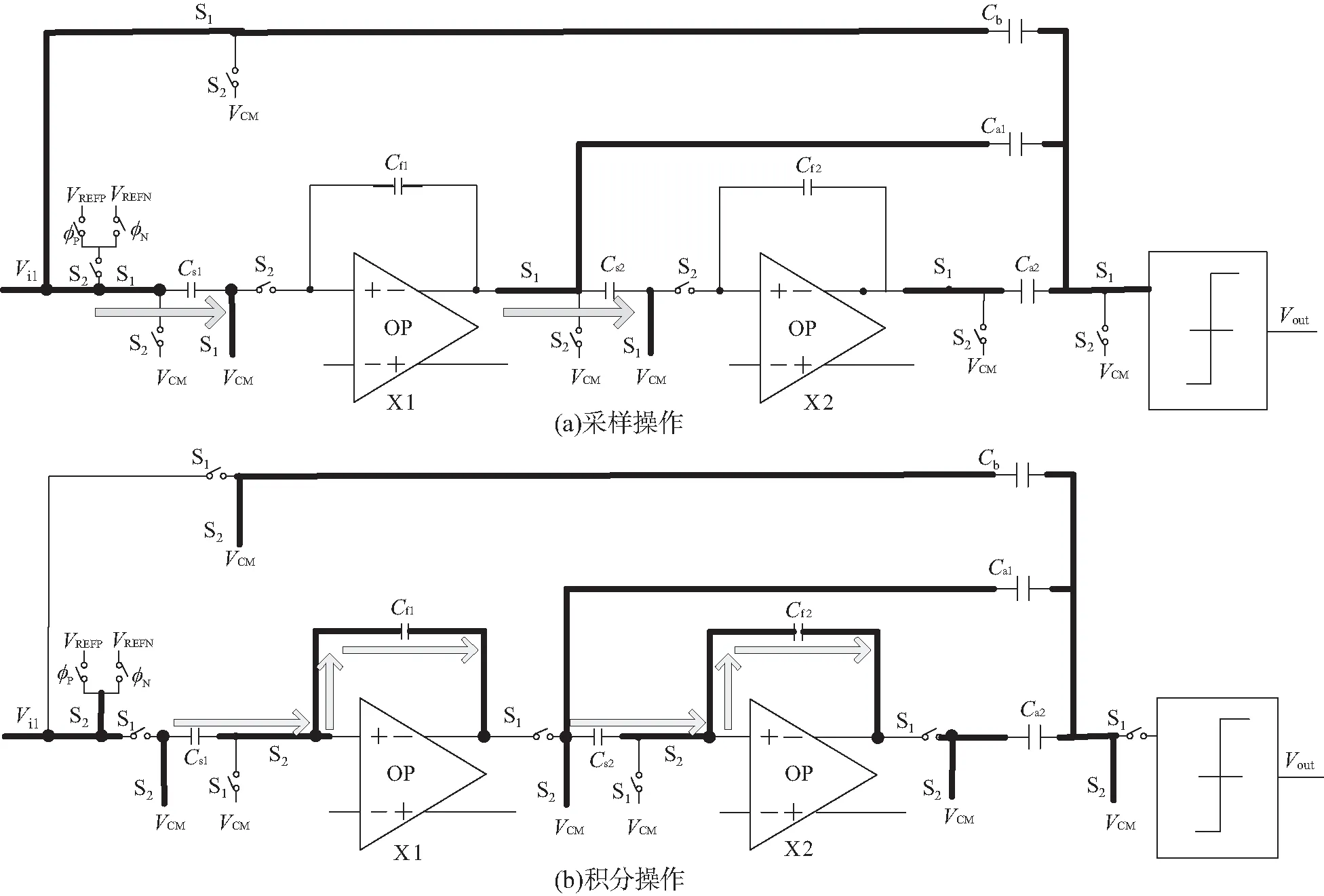
图8 传统的单环2阶Sigma-Delta调制器工作状态Fig. 8 Operating state diagram of a traditional single-ring second-order sigma-delta modulator

传统的单环2阶Sigma-Delta调制器的第一级和第二级噪声整形滤波器由不完全相同的积分器构成，往往第一级增益要求较高，第二级可以有所降低；而本文改进的单环2阶调制器将第一级高增益的噪声整形滤波器也应用在第二级，这反而可以提高调制器的精度。虽然改进的单环2阶调制器比传统的单环2阶调制器减少了一个噪声整形滤波器的使用，降低了功耗的同时也提升了精度，但是在图9可以看出，在内环和外环却比传统2阶调制器增加了2组开关，开关的增加势必会引入非线性因素。通过文献[19]所述改进型调制器结构增加的开关引入的噪声仅仅比传统结构调制器高出8%，在上文所述10%浮动范围内，相比于传统调制器结构，改进型调制器结构提升了精度和降低了功耗，且引入噪声范围在预设范围内，因此本文提出的基于浮动系数迭代思想的运放共享改进型低功耗高精度CIFF Sigma-Delta调制器是有实际意义的。

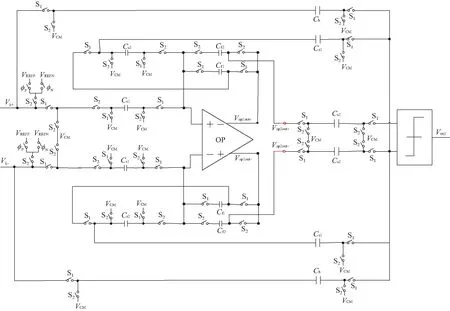
图9 基于浮动系数迭代思想的运放共享改进型低功耗高精度CIFF Sigma-Delta调制器原理Fig. 9 Schematic diagram of an improved low-power and high-precision CIFF sigma-delta modulator for op-amp sharing based on floating coefficient iteration idea

2.2 噪声整形滤波器设计

本文设计的Sigma-Delta调制器采用如图10所示的单级运放，并结合如图11所示增益提高，辅助运放(Gain Boost)构成噪声整形滤波器。未加入增益提高(Gain Boost)结构时，图10运放的直流增益为

Av=gm12{[(gm18+gmb18)ro18(ro12‖ro20‖ro22)]||[(gm16+gmb16)ro16ro14]}。

(10)

图10 运算放大器主电路Fig. 10 Main circuit of operational amplifier

Avtot=AvAgain。

(11)

但实际上，主运放和辅助运放对单位增益带宽(GBW)的选取也有一定要求，若辅助运放的单位增益带宽(GBW)小于主运放的单位增益带宽(GBW)，则会在主运放的频率特性中引入一个零极点对，从而对整个运放的建立特性产生较大影响[21-22]。

调制器应用于语音领域，设计需要留有一定的裕量, 因此设计单位增益带宽(GBW)为15 MHz，SR为20 V/μs, 相位裕度接近90°, 增益为110 dB。

为稳定运算放大器输出的共模电压，基于电荷分配原理设计了如图12所示的共模反馈电路，其中电容CMi(i=1,2,3,4)的大小需满足CMl=CM2，CM3=CM4。时钟Ck1、Ck2的控制开关S1、S2。S1断开S2闭合时电容CMl、CM2存储的电压值为VCMO-Vb5；S1闭合S2断开时将CMl、CM2存储的电荷分配给电容CM3和CM4，使得

VO++VO--2Vfb≈2(VCMO-Vb5)。

(12)

如果Vb5与Vfb所需要的理想电压非常接近，那么就可以保证VO++VO-≈2VCMO，从而达到稳定运放共模输出的目的。该共模反馈电路接在运放的输出端，电容CMl+CM3和CM2+CM4在S1闭合的时，可以看作运放输出端负载，等效于增大了运放负载电容，因此CMl～CM4的取值不宜过大。为了满足共模电压建立时间、精度，电容的选取一般遵循CMl=4CM3的原则。

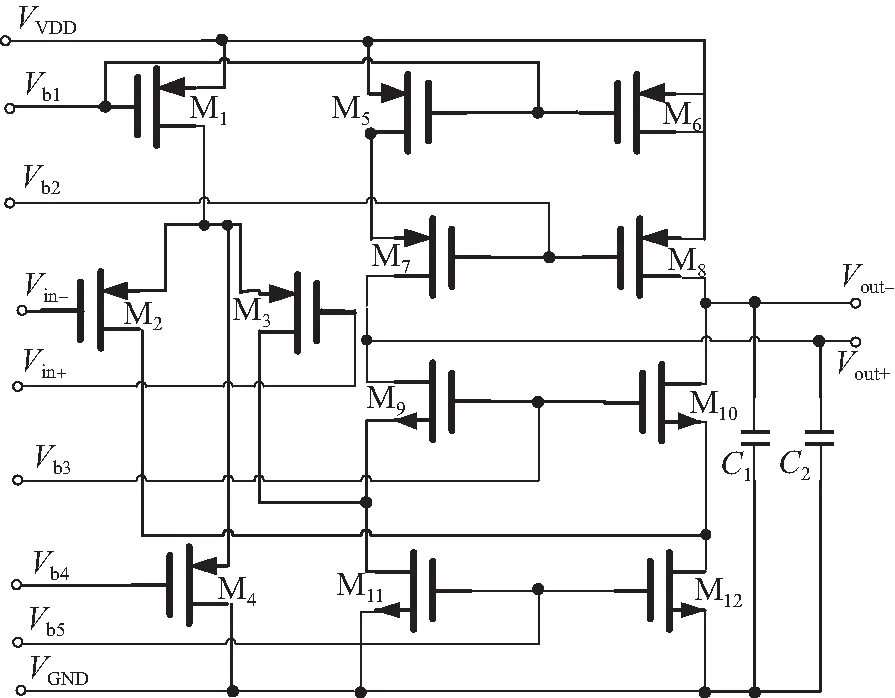
图11 辅助运放电路Fig. 11 Auxiliary Operational Amplifier

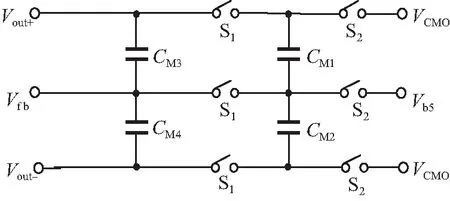
图12 共模反馈电路 Fig. 12 CMFB circuit

2.3 锁存比较器电路设计

Sigma-Delta调制器拥有的噪声整形技术会对比较器的offset进行处理[23]，因此对比较器的要求并不高，本文采用的比较器及其锁存单元如图13、14所示。通过时钟控制比较器工作在2个相位，PM4、PM5、NM0、NM1构成2个正反馈电路，VP1B=0时，比较器复位，把比较器输出节点和内部节点拉到VVDD，SB和RB被拉到VVDD，VP1B=VVDD时，比较器工作在放大区，原理同放大器PM2/PM0/PM1/PM3是复位管。

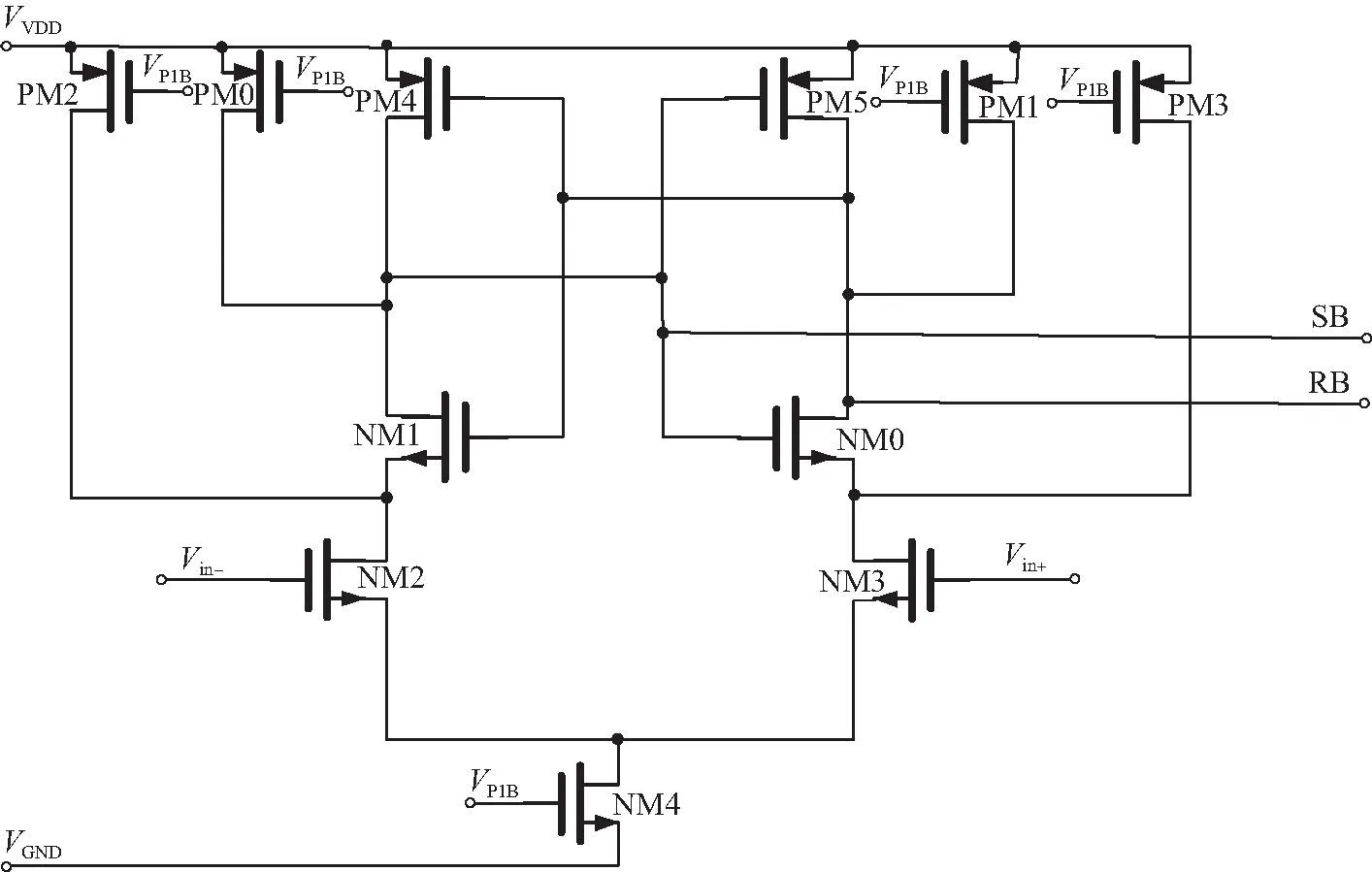
图13 动态锁存比较器Fig. 13 Dynamic latch comparator

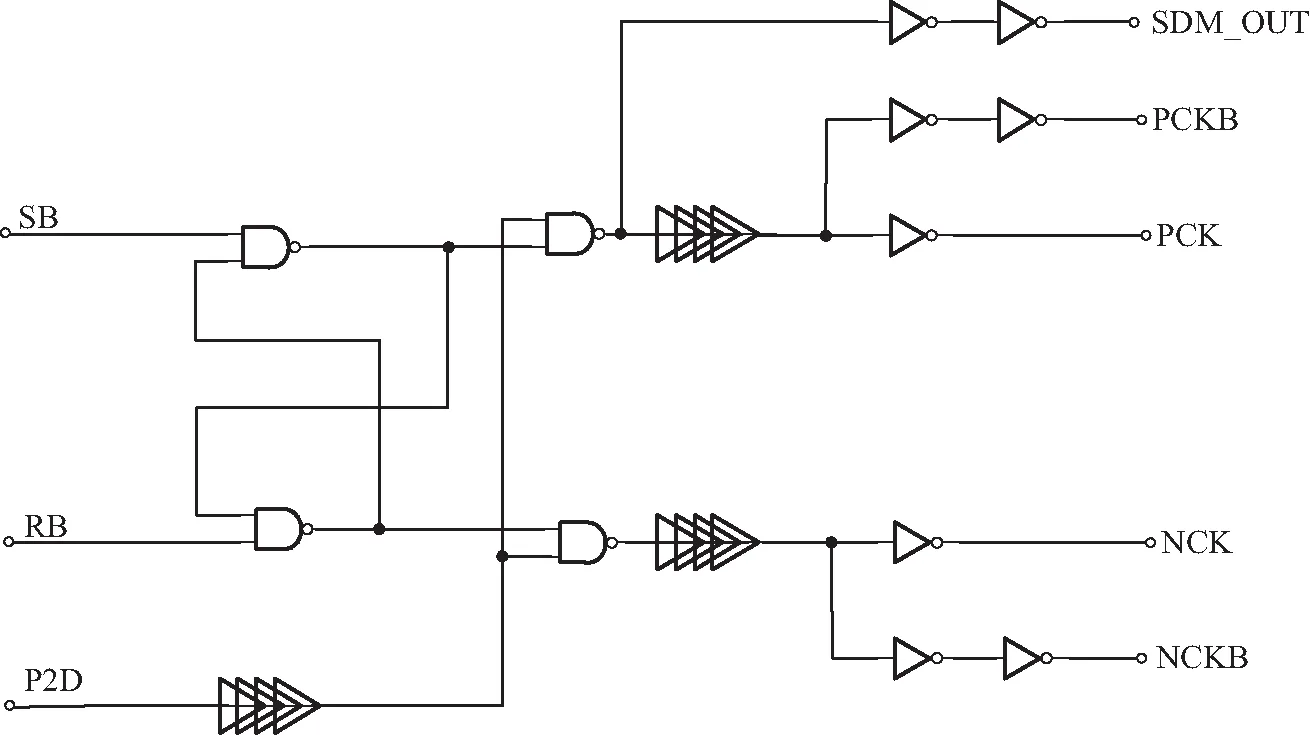
图14 动态锁存比较器逻辑单元Fig. 14 Dynamic latch comparator logic unit

3 Sigma-Delta调制器的版图与后仿结果

本文设计的Sigma-Delta调制器采用UMC 0.11 μm CMOS工艺，调制器版图如图15所示，其尺寸为226.8 μm×187.44 μm。

将350 mV @ 1.7 kHz的输入信号输入到图6本文设计的基于浮动系数迭代思想的运放共享改进型低功耗高精度CIFF Sigma-Delta调制器，将其输出的1 bit 码流导入到MATLAB中进行信噪比分析，输出频谱如图16所示，后仿真测试结果表明：在信号带宽为8 kHz、采样频率为4 MHz、供电电压为1.2 V时，该调制器输出的峰值信噪比为 98 dB，有效位数(ENOB)为16.1 bits。基于浮动系数迭代思想对调制器的系数筛选更加精确，更真实地将实际电路中存在的匹配和非线性因素反映到系数的选取上，为提升调制器精度提供了一个重要的思想指引。语音信号频率为300～3 400 Hz，因此本文设计的调制器满足语音芯片的应用需求。由于本文设计的调制器采用运放共享技术降低由噪声整形滤波器个数引入的额外功耗，因此调制器总功耗为290 μW。

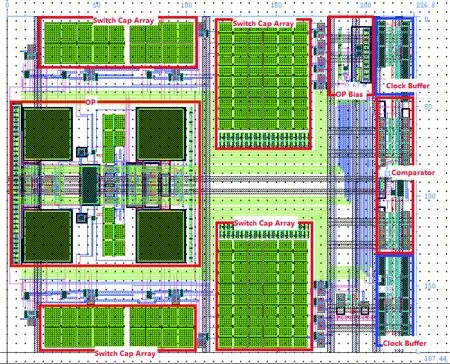
图15 本文设计的Sigma-Delta调制器版图Fig. 15 Sigma-Delta modulator layout designed in this paper

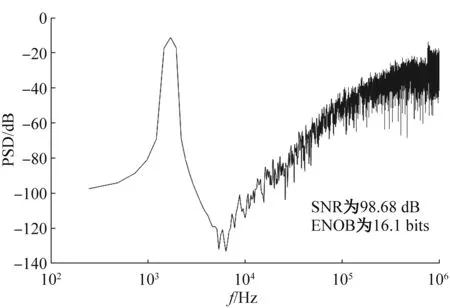
图16 本文设计的Sigma-Delta调制器输出频谱 (FFT of 213 points)Fig. 16 Output spectrum of sigma-delta modulator designed in this paper (FFT of 213 points)

本文设计的基于浮动系数迭代思想的运放共享改进型低功耗高精度CIFF Sigma-Delta调制器，在各工艺角下，后仿真得到的有效位数(ENOB)如表2所示。在版图设计时充分考虑了器件匹配，做好了对各个子电路模块隔离，因此版图仿真结果表明：在-40～125 ℃测试环境下，调制器的有效位数(ENOB)随着温度的降低有所提升，但在较高温度下略有下降。总体而言，该调制器有效位数(ENOB)受温度影响较小，具有实际应用意义，在各工艺角和各温度下的有效位数(ENOB)大于等于 15 bits，满足调制器预定精度要求。

FoM是衡量调制器性能的主要指标，根据品质因数figure-of-merit(FoM)来标准化能量消耗百分比的位(EENOB)，式(13)为能量消耗计算公式，式中NFoM代表品质因数(FoM)，PPOWER和BBW分别是调制器的总功耗和输入信号带宽。式(14)中EENOB为有效位数。

表2 不同工艺角下调制器的有效位数

(13)

(14)

表3为近年国内外设计的Sigma-Delta调制器各项参数对比情况，从表中可以看出，本文设计的Sigma-Delta调制器可以实现低功耗高精度的AD转换。

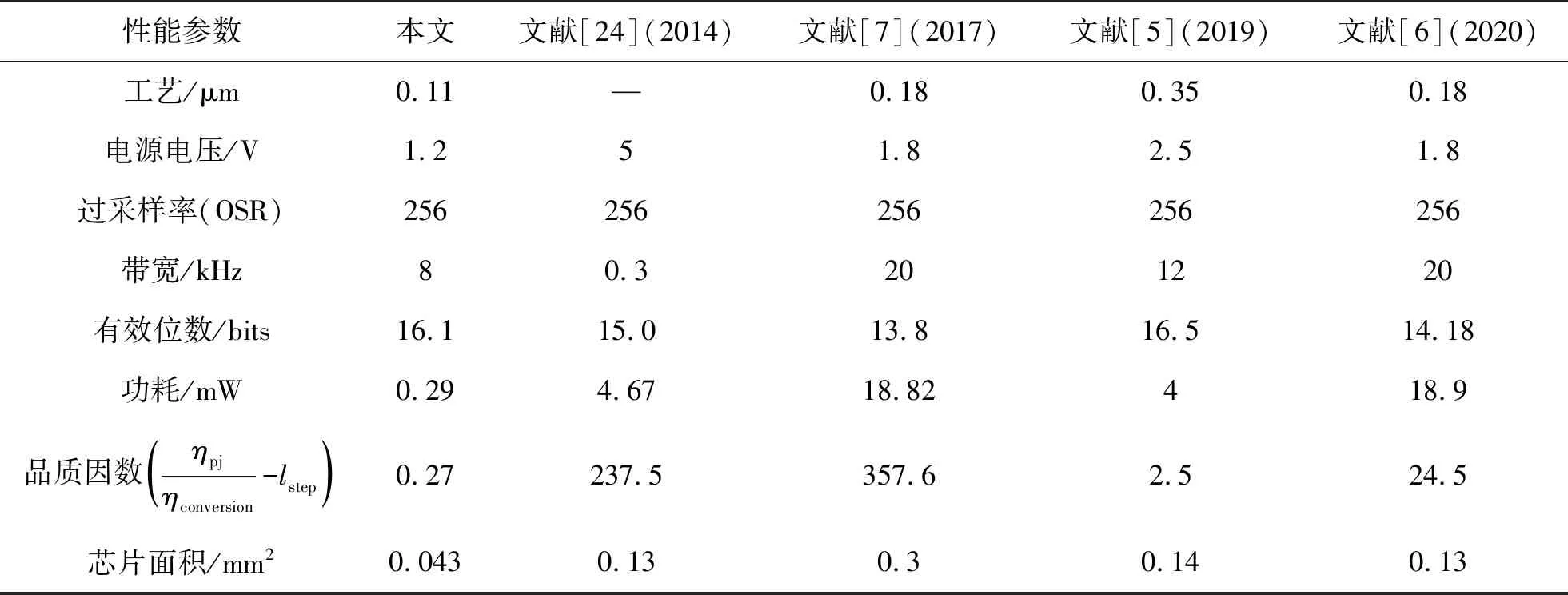
表3 调制器性能对比

4 结语

本文设计了一种应用于语音领域基于浮动系数迭代思想的运放共享改进型低功耗高精度CIFF Sigma-Delta调制器，通过运放共享技术降低了传统2阶调制器结构中2个噪声整形滤波器引入的功耗，并将浮动系数迭代思想应用于系统及设计获取系数，使得调制器的精度提升了0.27 bit。在UMC 0.11 μm CMOS工艺下完成了整个调制器原理图和版图的设计，后仿真的结果表明：该调制器在输入信号带宽为8 kHz、过采样率为256时，输出的有效分辨率达到16 bits，满足预定设计指标要求。