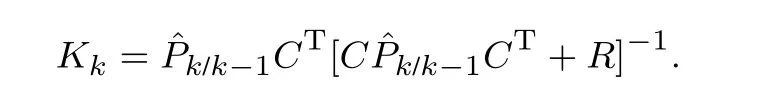针对工业信息物理系统中的拒绝服务攻击建立检测模型
2020-05-12庄康熙孙子文
庄康熙孙子文
(1.江南大学物联网工程学院,江苏无锡 214122;2.物联网技术应用教育部工程研究中心,江苏无锡 214122)
1 引言
近年来,由于计算机、通信和相关硬件技术的飞速发展,信息物理系统(cyber physical systems,CPS)的理论和应用也迅速发展.作为一个新的研究领域,与传统的独立于物理系统外的网络系统不同,CPS是一个综合计算、网络和物理过程,集计算、通信和控制为一体的多维复杂系统.为了实现网络和物理对象之间的紧密交互,CPS通常采用交互式元件,如智能传感器、执行器和控制器等嵌入式设备用以感知、监测和控制物理世界.工业信息物理系统(industrial cyber physical systems,ICPS)是工业环境中的CPS,广泛应用于关键基础设施,如现代化工厂、配水网络系统和智能电网等[1].
由于无线通信网络比较脆弱,导致ICPS易遭受拒绝服务(denial of service,DoS)攻击、重放攻击和欺骗攻击等网络攻击,对系统的稳定性和安全性造成威胁.有报道的第一个成功攻击工业控制系统的是震惊世界的伊朗震网(Stuxnet)病毒事件[2].由于ICPS对实时性的要求很高,攻击造成的数据包延迟或丢失等会大幅度地降低系统性能.若ICPS系统被成功入侵而未被检测到,将导致信息丢失,工厂基础设施遭到破坏,国家经济受到损失甚至会危及生命等严重的后果[3].目前的ICPS中的攻击者是智能攻击者,可以利用窥测得到的系统知识制定攻击策略以保证不被发现,如文献[4]通过已知的系统知识提出了一种线性欺骗攻击策略,基于相应的可行性约束,使得攻击者能成功注入虚假数据而未被检测到.提高ICPS的安全性十分重要[5–6],尤其是ICPS中攻击检测的研究.不同于传统的工业系统故障检测,ICPS攻击检测更具挑战性[7].
针对ICPS中的攻击,研究者从攻击者的视角,有零星的文献从控制理论的角度研究ICPS中的攻击模型,包括攻击模型的不同表达.由于DoS攻击对无线通信网络造成的严重破坏,导致大量数据包的丢失,严重威胁了网络控制系统的运行[8].文献[9]描述了在系统安全即稳定性和资源约束包括能源、时间和通信限制下的CPS在滤波和控制方面的最新进展,并给出了DoS攻击、重放攻击和欺骗攻击3种网络攻击的基于攻击效果的简单模型.文献[10]提出了由先验系统模型知识、披露资源和破坏资源组成的三维攻击空间的概念,对DoS攻击、重放攻击、本地零动态攻击和偏差注入攻击进行了3个维度的分析,给出了基于攻击资源的具体攻击模型.已经有一些数学模型被用来定量分析攻击导致的性能退化,如排队模型[11–12]、伯努利模型[13]或马尔可夫模型[14].
针对ICPS中的DoS攻击检测,文献[15]尝试在网络流量上使用密度聚类算法来实现基于异常的分布式DoS攻击检测和防范,但数据的属性和参数的选择对于基于密度的聚类算法影响较大.文献[16]为了检测DoS 攻击提出了一种同时检测已知攻击和未知攻击的检测系统,采用多元相关分析技术提取网络流量之间的几何相关性,进而用来检测DoS攻击,但特征的选择较为复杂,会较大的影响攻击检测率.文献[17]提出了一种可信的自组织网络路由建立了基于概率包标记的攻击源可靠定位模型对DoS路由攻击进行攻击检测,但是自组网络节点环境较为复杂,对所有节点行为的描述识别是难以完成的.以上文献从数据流、路由等角度采用聚类或多元相关分析技术等方法从不同角度给出了不同的检测方法,有各自的优缺点,且方案执行的复杂度较高,导致检测方案成本较高并且可行性较低.
为有效地检测ICPS中的DoS攻击,本文研究了一种基于反馈控制理论建模的攻击检测模型.采用卡尔曼滤波器和χ2检测器[18]相结合的检测方案,在反馈回路中,卡尔曼滤波器用于去除环境噪声并能在系统遭受攻击时减小攻击噪声对测量残差的影响;攻击的存在会导致不同于正常状态下的测量残差水平,故基于二元假设检验理论,建立χ2检测器检测测量残差的统计值,达到检测DoS攻击的目的.
2 带攻击检测的ICPS建模
为检测ICPS中的攻击,立足线性时不变控制系统得到系统的输入输出状态,结合卡尔曼滤波器对系统的状态进行最优估计,从而检测ICPS中的网络攻击.其基本思想是将攻击时对传感器产生的影响视为“攻击噪声”,采用估计器对攻击噪声进行统计行为估计,从而建立起攻击检测判决规则.
2.1 离散状态空间ICPS模型
ICPS的整体框架如图1所示[19].其中:无线传感器网络是由多个传感器组成的用于监视物理环境的网络拓扑结构,执行器网络是由多个执行器组成的用于更改物理参数的网络拓扑结构.
由于系统中存在环境噪声干扰且容易遭受各种网络攻击,故在图1基础上,增加状态估计器和检测器,对ICPS控制模型建模如图2所示[18].
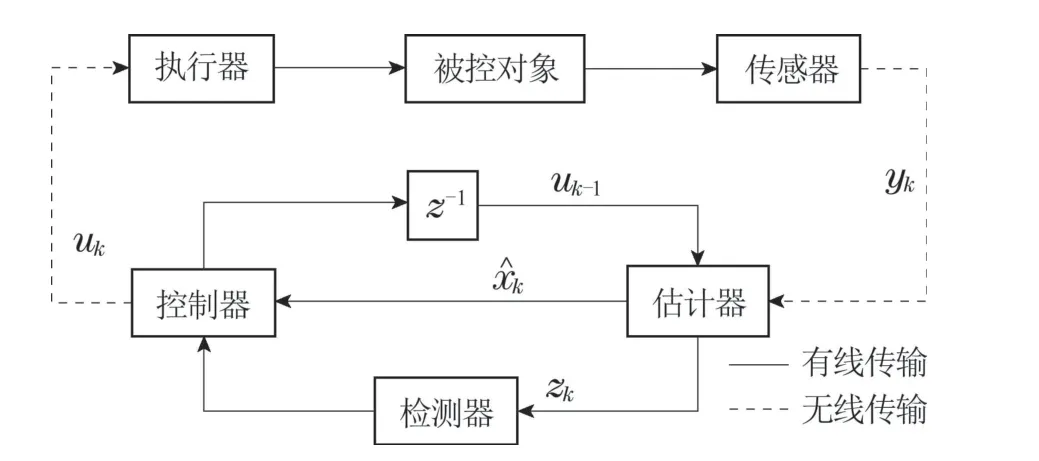
图2 ICPS控制模型Fig.2 ICPS control model
其中,估计器用于去除噪声,包括工业环境噪声和攻击时产生的攻击噪声,并对系统进行最优估计;检测器用于检测系统故障和检测系统是否受到网络攻击的影响.估计器采用卡尔曼滤波器,检测器采用基于测量残差水平的χ2检测器[20–21].
2.2 离散状态空间ICPS模型分析
2.2.1 离散线性时不变系统数学模型
对于被控对象,考虑以下离散线性时不变系统:
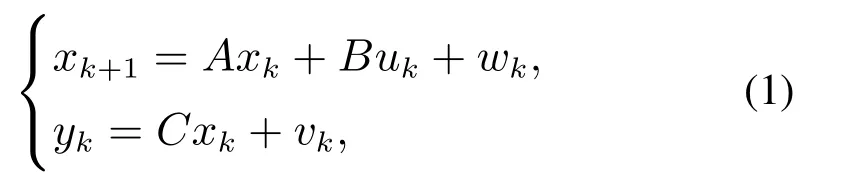
其中:下标k ∈N为观察时刻,xk,uk和yk分别为系统的状态向量、控制向量和测量向量;A,B和C分别表示状态转移矩阵、控制矩阵和测量矩阵;wk ∈Rn为系统噪声,vk ∈Rn为测量噪声,两种噪声均为高斯白噪声且两者相互独立,即wk~N(0,Q),vk~N(0,R).
正常情况下,传感器测量被控对象得到测量值yk,并通过无线通信网络将测量值yk传输给估计器进行最优状态估计,估计器估计出最优状态ˆxk并得到测量残差zk;检测器接收测量残差zk用于检测分析,控制器接收状态估计并给出控制信号uk,再通过无线通信网络将控制信号uk传输给执行器,从而驱动被控对象达到理想状态.初始状态x0~N(0,P0),并且对于所有的k≥0 都独立于wk和vk.
2.2.2 状态估计器
状态估计器采用卡尔曼滤波器,以减小系统噪声和测量噪声对系统的干扰.卡尔曼滤波器是一种高效的递归滤波器,它能够通过系统的输入和输出观测数据,从包含噪声的测量中得到系统状态的最优估计量.
对于离散线性时不变系统(1),系统噪声wk和测量噪声vk的存在导致系统的测量值yk通常是不准确的,因此需要基于实际测量值yk对系统状态xk进行估计.使用卡尔曼滤波器能剔除噪声减轻噪声对控制系统的影响,并减小噪声对检测器检测率的影响.其去噪处理分为时间更新和测量更新,具体步骤如下.
1)时间更新.
首先,根据k −1时刻的估计值来预测当前k时刻的估计值:
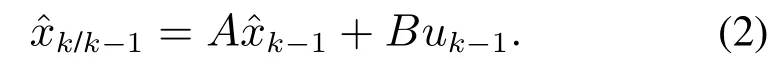
然后,通过实际值和预测估计值的残差得到预测误差,即由式(1)和(2)得
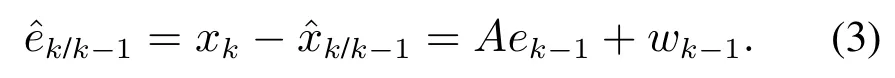
再通过预测误差计算其误差协防差:
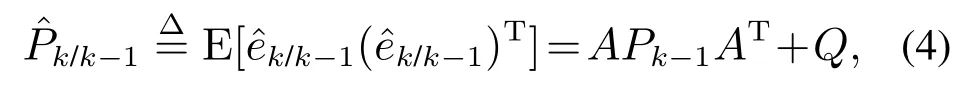
其中Pk−1为上一时刻估计误差的最小协方差.但是仅为预测估计值的误差协方差,而非最终估计值的误差协方差.将用于计算最优卡尔曼增益Kk.
2)测量更新.
在时间更新的基础上,结合当前k时刻的测量值yk,即可进行测量更新.
首先,计算卡尔曼增益Kk(计算过程详见附录):
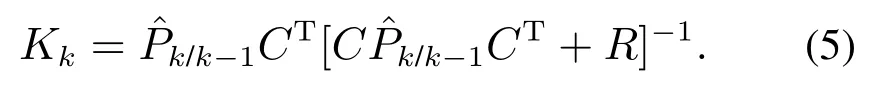
采用卡尔曼增益更新当前k时刻的系统状态估计:
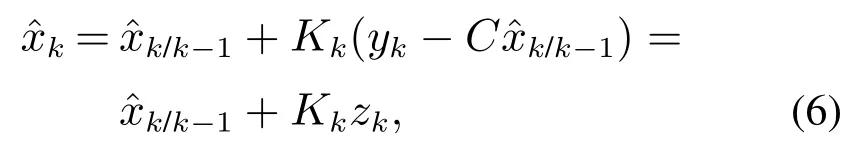
其中,测量残差
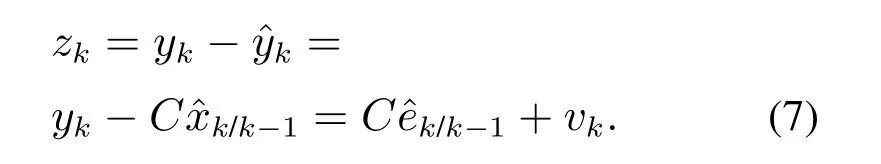
实际测量值与预估测量值的测量残差zk和系统状态估计值均为卡尔曼滤波的输出,分别用于检测和控制.
进一步得到状态估计值的误差:
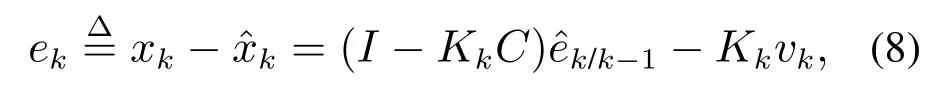
其中I为单位矩阵.
最后得到状态估计误差的最小误差协方差:
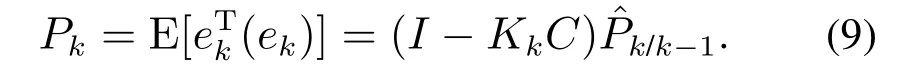
通过测量更新得到的k时刻的最优估计值ˆxk和最小误差协方差Pk将作为已知量用于k+1时刻的时间更新.
为了保证整个卡尔曼滤波器去噪迭代过程的顺利进行,需要给定系统一个初始估计值和任意一个有限正定的初始估计误差的协方差P0.对于任意一个有限正定的P0,通过卡尔曼滤波器的去噪处理后协方差矩阵将以指数速度收敛到一个固定值[22].由于协方差矩阵会迅速收敛到一个固定值,故卡尔曼增益Kk虽在每个时刻更新,但在几次迭代后也将快速收敛并且在稳定状态下运行[23].
2.2.3 χ2检测器
χ2检测器能对测量残差zk的细微的变化进行放大及标准化,得到其具有卡方分布的统计特性.由于通过卡尔曼滤波器得到的实际测量值与预估测量值的测量残差zk是正负相间且变化细微的,直接用于检测的效果很差,故使用χ2检测器通对测量残差zk的统计特性进行标准化进而监控系统行为.
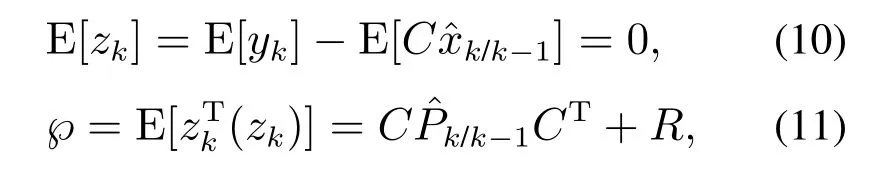
由残差式(7)计算测量残差的均值及其协方差:可得在非攻击状态下测量残差zk服从高斯独立同分布,均值为0且协方差为.
通过测量残差zk及其协方差为℘,构造测量残差zk的卡方分布并对其进行标准化,得到检测值:
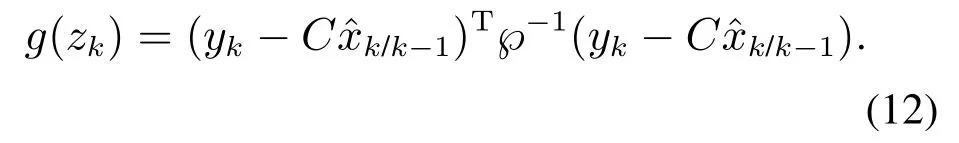
2.3 DoS攻击下的离散状态空间ICPS模型分析
DoS攻击是一种使系统资源变得不可用的网络攻击.DoS攻击通过各种手段消耗网络带宽和系统资源,或者攻击系统缺陷,阻塞共享网络介质以防止设备进行通信或接收数据,使系统的正常服务陷于瘫痪状态,从而达到拒绝合法用户正常访问数据的目的.
从攻击原理来看,攻击者可以占用用户域或内核域的缓冲区,阻塞共享网络介质以防止设备进行通信或接收信号,即阻断传感器测量数据和控制器信号到达目的地的通道.基于此原理,建立DoS攻击下的系统模型,如图3所示.
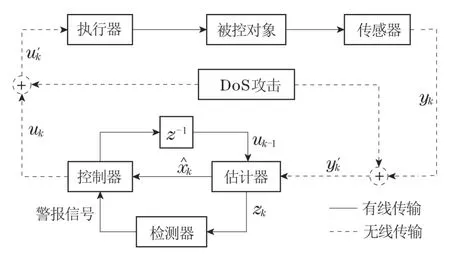
图3 DoS攻击下的控制模型Fig.3 Control model under DoS attack
2.3.1 DoS攻击下的系统数学模型
假设DoS攻击同时攻击传感器测量值和控制器输出的控制信号,从而导致数据的缺失.虽然DoS攻击和测量数据丢失之间存在不同的物理机制,但它们的数学模型在伯努利框架中是相同的,故通过典型的测量数据丢失方法来分析受到DoS攻击的ICPS的性能是可行并且有效的[19].因此,采用伯努利模型建模DoS攻击.
使用离散线性时不变系统模型(1)并对传统的伯努利模型进行改进,建立DoS攻击下离散线性时不变系统数学模型.为了对缺失的数据建模,使用数字控制器来处理当前不可用的数据,缺失的当前时刻的测量值yk和控制信号uk值用前一次接收的数据yk−1和uk−1代替[10].因此,在DoS攻击下估计器接收到的测量值可以看作是测量值yk加上攻击信号(yk−1−yk)后的结果,执行器接收到的控制信号可以看作是控制信号uk加上攻击信号(uk−1−uk)后的结果.得到基于伯努利模型的离散线性时不变系统模型:
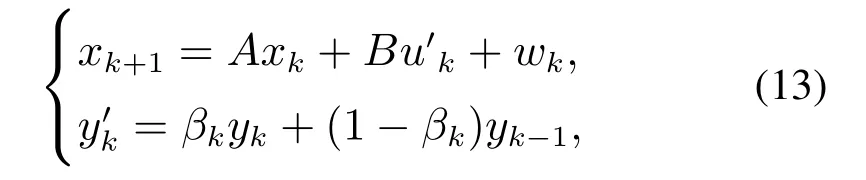
其中攻击下的控制器u′为
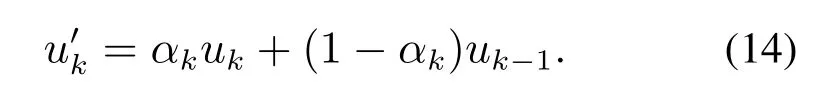
式(13)和(14)中的αk和βk用于表示伯努利过程中的有无攻击,故只能取0或1.正常情况下,αk和βk均取1,此时将式(14)代入式(13)即可得到正常情况下的离散线性时不变系统模型(1);当系统遭受DoS攻击时,根据攻击者攻击策略和攻击资源的不同,αk和βk的取值可分为以下3种情况:
1)攻击者只对传感器通道进行攻击:此时αk=0,βk=1;
2)攻击者只对反馈控制通道进行攻击:此时αk=1,βk=0;
3)攻击者同时对两个通道进行攻击:此时αk=0,βk=0.
为了检验所研究的攻击检测模型在面对强大攻击者攻击时的检测性能,假设攻击者掌握了较为充足的攻击资源,可同时对两个通道进行攻击,此时αk=0,βk=0,得到DoS攻击下的测量值,控制信号.
2.3.2 DoS攻击下的状态估计器
在攻击状态下,结合式(13)和(14)即可得到DoS攻击时卡尔曼滤波器去噪处理的过程.
1)时间更新.
基于模型(13)–(14),推导DoS攻击下的卡尔曼滤波器去噪处理的更新方法,状态值、误差值和误差协方差的更新分别如式(15)–(17):
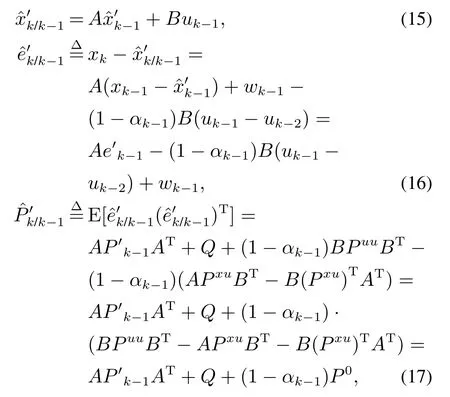
其中:Puu=E[(uk−1−uk−2)(uk−1−uk−2)T]为攻击状态下控制作用之间的协方差,Pxu=E[(xk−1−为系统状态与控制作用之间的协方差.为对比式(4),引入P0以突出攻击状态下误差协方差的不同,其中P0=BPuuBT−APxuBT−B(Pxu)TAT.
2)测量更新.
依据时间更新值,计算DoS攻击下的卡尔曼增益:
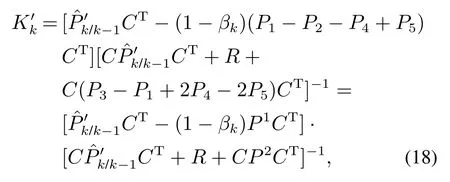
更新当前k时刻的系统状态估计、估计值误差及其最小协方差,如式(19)–(21):
2.3.3 DoS攻击下的χ2检测器
DoS攻击下的检测器接收到的测量残差:

为对比式(7),引入βk和z0以突出攻击状态下测量残差的变化,其中
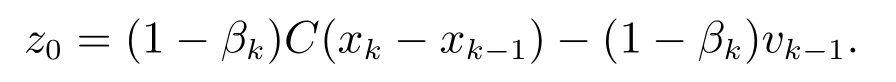
进一步求得攻击状态下测量残差的协方差:
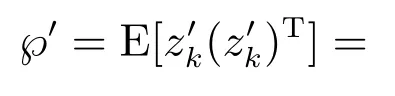
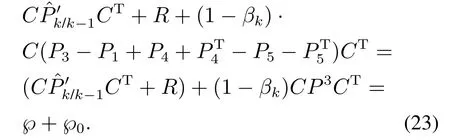
为对比式(11),引入P3和℘0以突出攻击状态下较正常时测量残差协方差的变化,其中:P3=P3−P1.

2.4 DoS攻击检测判决规则
分别对比分析式(9)与(22),(11)与(23)以及(12)与(24)可知,当系统受到DoS攻击时,会产生不同于正常状态下的测量残差、从而导致不同的协方差和检测值.故提出二元假设检验方案,来判断攻击的存在是否造成了不同的检测值.零假设H0和代替假设H1定义如下:
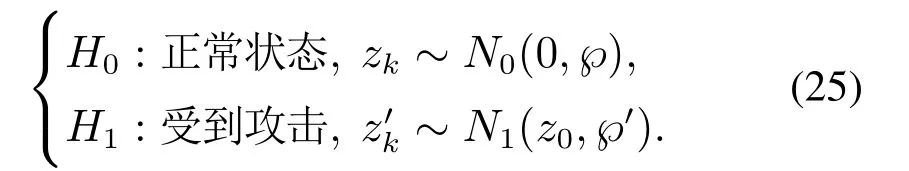
基于二元假设检验的检测器检测方案,给出以下DoS攻击判决规则[18]:
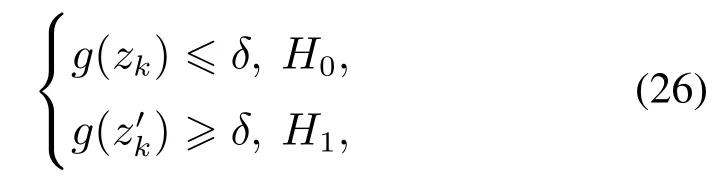
其中δ为用以判断系统是否受到攻击的阈值.δ是对具体的被控对象进行训练并考虑不同攻击时间下的虚警率(false alarm rate,FAR)和漏警率(missing alarm rate,MAR)等参数指标综合设置得到的.虚警率和漏警率的大小受δ的影响,随着阈值增大虚警率会变低而漏警率将变高,随着阈值减小漏警率会变低而虚警率会变高.折衷考虑虚警率和漏警率,当攻击强度、攻击时间不同时,选取等错率作为阈值的确定依据,即漏警率和虚警率相等且都较小时的δ作为阈值.
若系统正在遭受攻击并被成功检测到,检测器将触发警报信号,并将信号作用于控制器以减少攻击时控制器的影响.本文重点解决攻击检测问题,警报信号的具体产生及采用何种有效的处理方法来减小攻击对系统的影响是下一步研究的重点.
3 仿真与结果
本文采用Simulink/TrueTime仿真软件,通过将DoS攻击转为典型的测量数据丢失的方法进行分析和仿真,对所提出的二元假设检验理论进行仿真验证,进而检验检测器对ICPS中的DoS攻击的检测效果.为模拟实际系统,本文将球杆系统作为被控对象,并以控制小球的位置为目标,来验证所提出的二元假设检验方案,并检验检测器的效果.
3.1 被控对象的数学模型
球杆系统是一个通过控制导轨俯仰角,使轨道上的小球稳定在指定位置上的装置.小球可以在导轨上自由滚动,导轨的一端由支撑转轴固定,另一端可通过电机传动机构带动进行上下活动,从而产生倾斜角使小球滚动[24].
对球杆系统进行建模分析如图4所示,其中转盘的转动角度θ为输入即控制信号u,输出为小球的位置l即传感器测量值y,由于球杆系统运行过程中导轨偏角a和转盘的转动角度θ变化范围都较小,因此可以认为两端划过的弧长相等.当导轨倾角变化θ时,小球向下滚动,根据牛顿运动定律可得
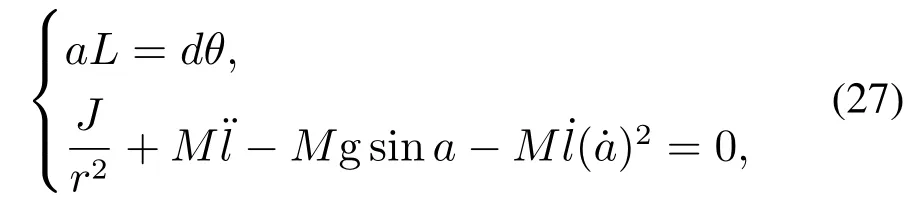
其中:L为导轨长度,d为转盘半径,M为小球质量,r为小球半径,J为小球的转动惯量,g为重力加速度.
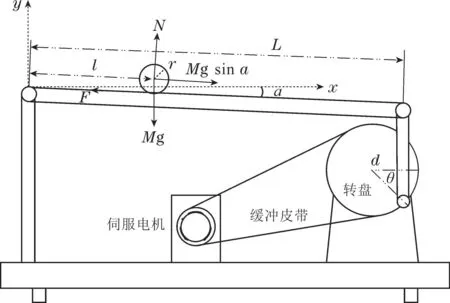
图4 球杆系统的建模分析图Fig.4 Modeling analysis diagram of the ball-beam system
小球大致平稳后,导轨几乎处于水平状态,因此a趋近于0,故可以在a=0的邻域内对其进行线性化处理,即sina ≈a,对式(27)进行简化、合并得到输出l即测量值y与输入θ即控制信号u的关系式:
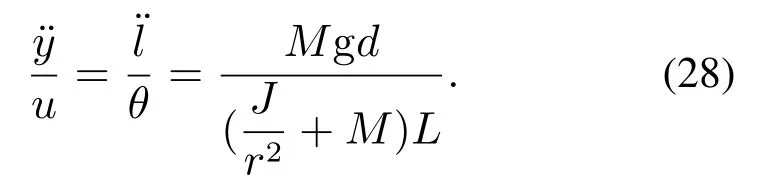
对式(28)进行拉普拉斯(Laplace)变化,得到测量值y(s)与控制信号u(s)的传递函数:
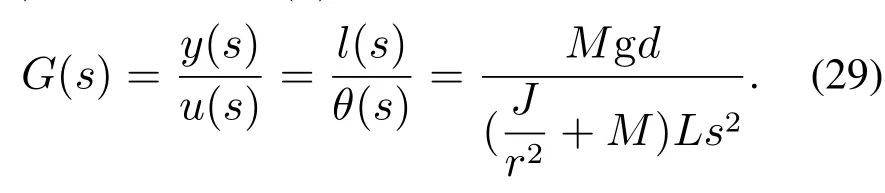
球杆系统的参数设置如表1所示.
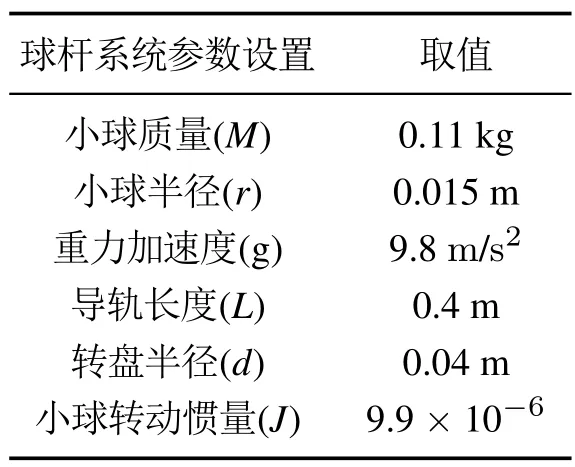
表1 球杆系统参数Table 1 The ball-beam system parameters
将各参数值代入式(29),可得
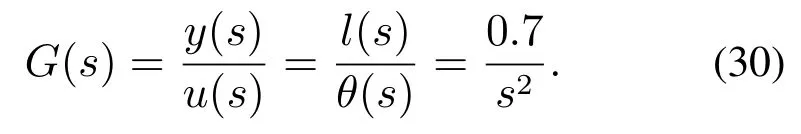
将传递函数转化为状态空间方程并在采样周期为1 ms下进行离散化,得到离散状态空间方程:
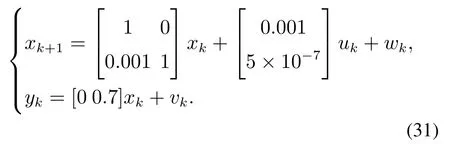
对比式(1)可知,
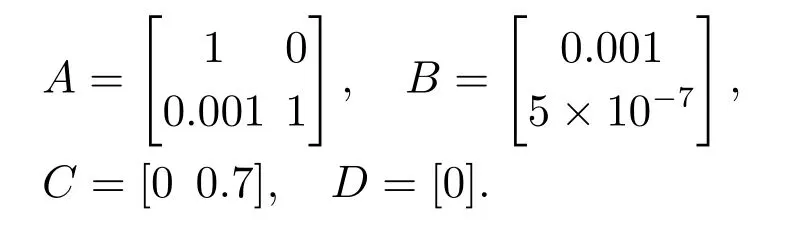
3.2 系统仿真及分析
小球初始位置为0 m(导轨最左端),控制目标是让小球停在导轨正中间0.2 m处,将离散状态空间方程(31)作为被控对象进行仿真系统的搭建.通过仿真得到,正常情况下存在环境噪声干扰以及经过卡尔曼滤波器过滤后的系统仿真图如图5所示.通过对比图5中滤波前后的波形可知,卡尔曼滤波器对噪声具有很好的过滤效果.
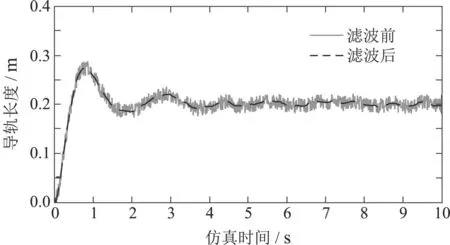
图5 卡尔曼滤波器对小球位置控制的影响Fig.5 Effect of Kalman filter on ball position control
3.2.1 对小球位置的控制
经过卡尔曼滤波器滤波后得到对小球位置的控制如图6所示.分析图6可知,球杆系统的超调量为35%,上升时间为0.39 s,3.14 s 后小球的位置在(0.2±0.009)m范围内来回滚动,偏差小于5%,故调节时间为3.14 s,之后系统处于稳定状态.当小球位置稳定后,在(7.4~7.65)s内对系统进行DoS攻击,得到受攻击影响的小球位置控制图如图7所示,对比图6和图7可以看出系统受到攻击后出现较大波动,对系统的稳定性造成了较大影响.由于发生攻击时,卡尔曼滤波器采用上一时刻的测量值来代替这一时刻的值继续进行估计,故攻击造成的影响逐渐增加,当攻击停止后,由于控制器的调节作用系统又逐渐稳定.
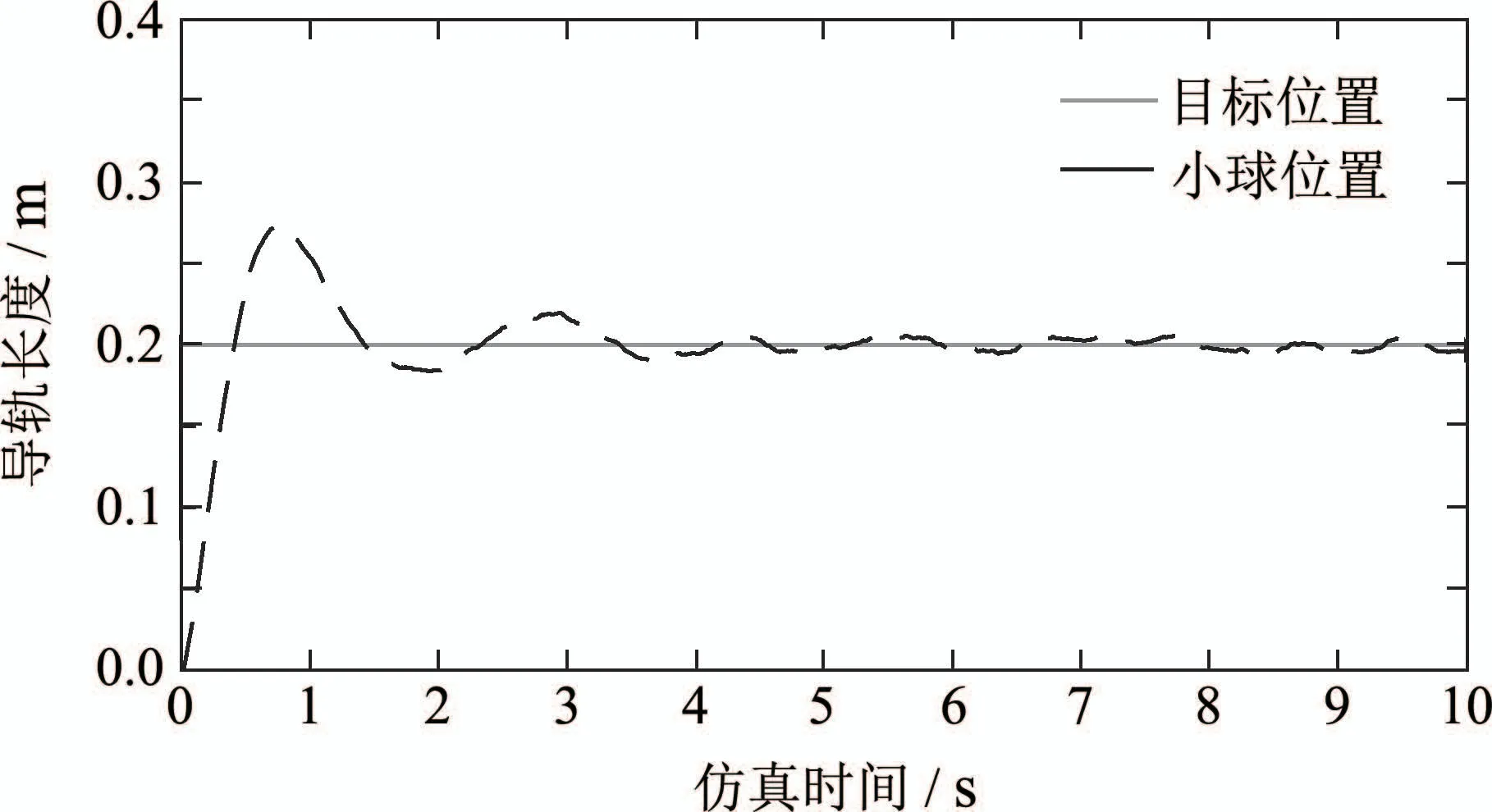
图6 正常情况下对小球位置的控制Fig.6 Control of the ball position under normal conditions

图7 DoS攻击下对小球位置的控制Fig.7 Control of the ball position under DoS attack
3.2.2 检测结果与对比
通过χ2检测器得到正常和受攻击影响时的检测值分别如图8和图9所示.对比分析可知,正常情况下通过卡方检测器得到的检测值g(zk)基本稳定在一定范围内,当系统遭受攻击时,检测值g(z′k)较正常时显著增大.对于图9,由于在攻击时间(7.4~7.65)s内检测值g(z′k)显著增大,从而验证了式(25)所提出的二元假设检验理论.通过选定合适的阈值δ,当发生攻击时,受攻击影响若检测值g()增大并而超出阈值δ,检测器便可检测出攻击的存在.
为了验证检测模型中χ2检测器的优越性,使用欧几里得检测器作对比实验.欧几里得检测器通过计算数据测量值与预估值之间的偏差来检测虚假数据攻击[25],其计算式为
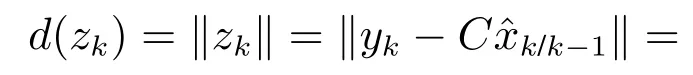
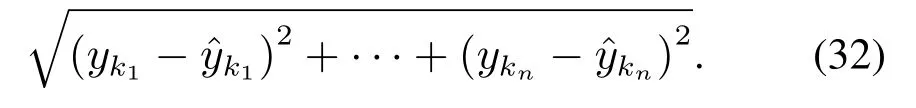
与χ2检测器相同的是,通过设定阈值,当检测值d(zk)超过阈值时也会触发警报;不同的是欧几里得检测器仅是单纯的通过实际值与估计值的偏差来进行检测,而卡方检测器通过测量残差zk的卡方分布并对其进行标准化得到检测值.
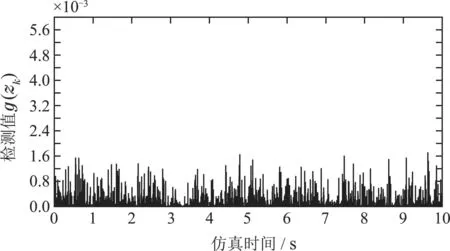
图8 正常情况下的χ2检测值g(zk)Fig.8 Chi-square detection values g(zk)under normal conditions
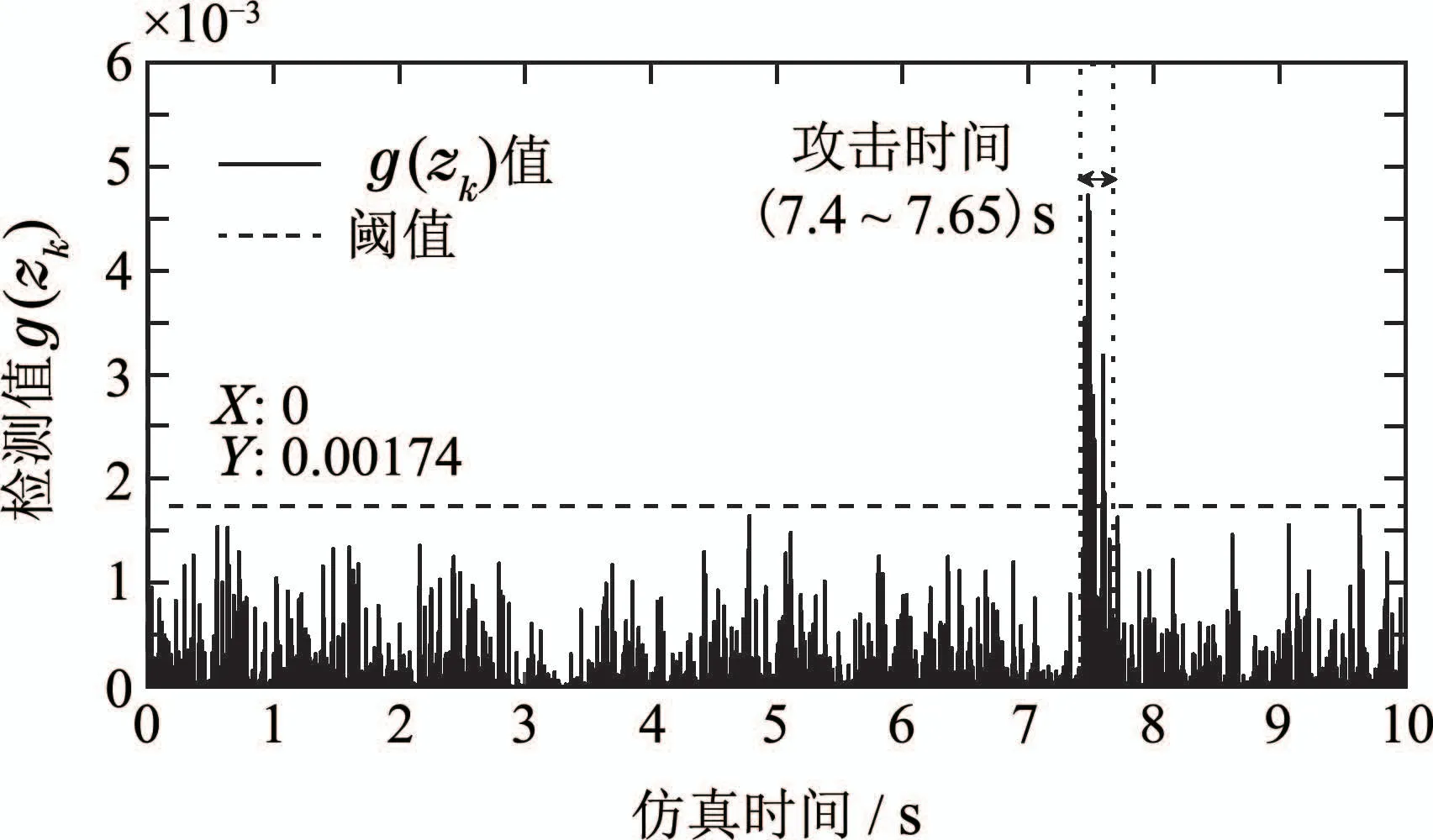
图9 DoS攻击下的χ2检测值g()Fig.9 Chi-square detection values g()under DoS attack
正常情况下,使用欧几里得检测器得到的检测值d(zk)如图10所示.在(7.4~7.65)s内对系统进行DoS攻击,遭受攻击时的检测值d(z′k)如图11所示.对比图10和图11可知,受攻击影响,检测值d(zk)同样会发生一定地变化.因此,通过设置合适的阈值,欧几里得检测器也可用于DoS攻击检测.

图10 正常情况下的欧几里得检测值d(zk)Fig.10 Euclidean detection values d(zk)under normal conditions
对比图9和图11,两种检测器在攻击期间内的检测值均发生明显突变,故均可用于检测DoS攻击,但卡方检测器在攻击阶段的检测值g()相较于欧几里得检测器的检测值d()的突变更加明显.
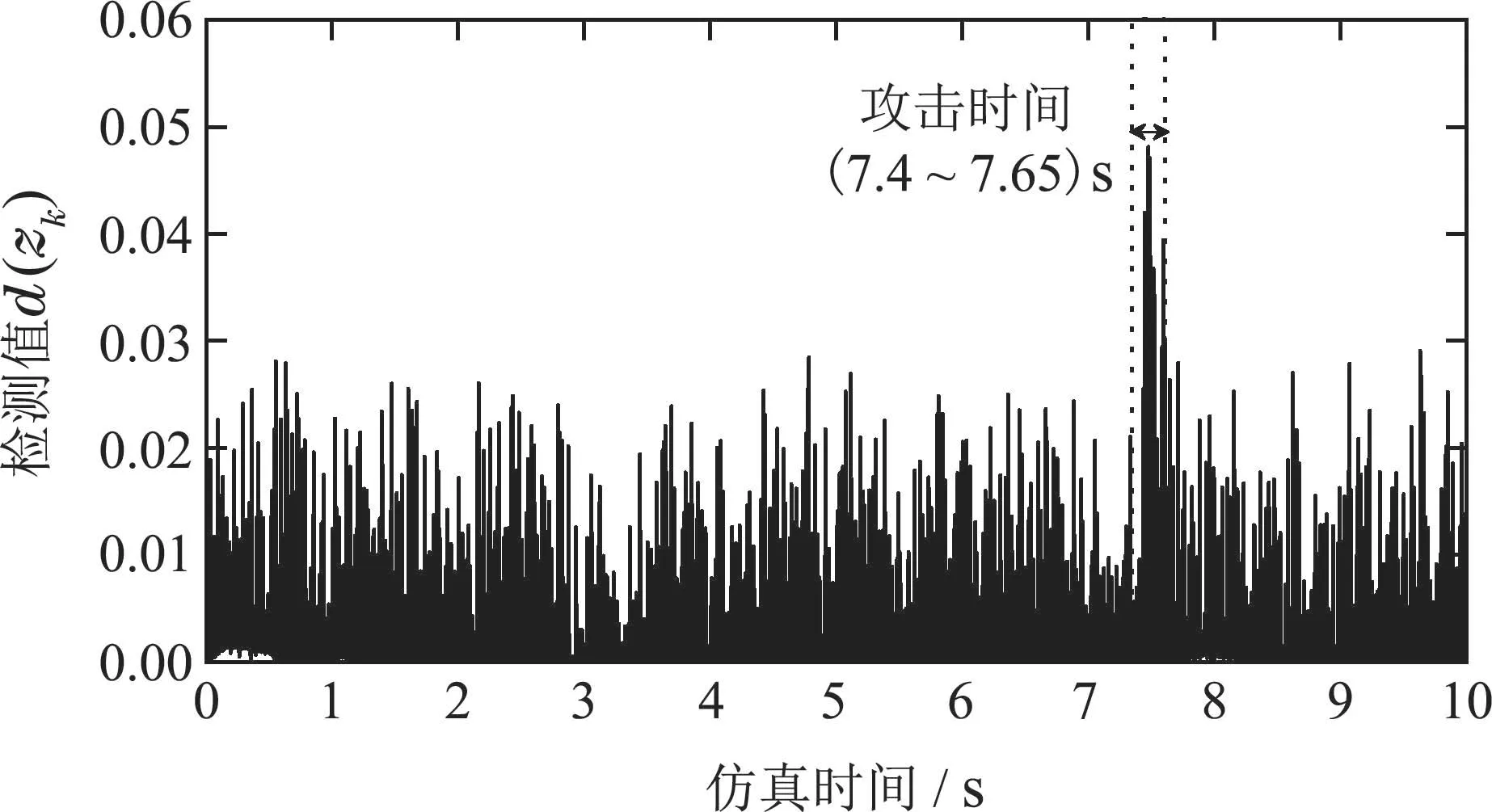
图11 DoS攻击下的欧几里得检测值d()Fig.11 Euclidean detection values d()under DoS attack
3.2.3 阈值的选定
为验证检测器性能,首先基于攻击有效率设定攻击持续时间,再通过等错率分别对两种检测器选择合适的阈值.基于第2.3.1节所提出的伯努利模型,考虑到攻击时间长度的不同对系统造成影响不同,若攻击时间较短,攻击对小球位置的影响会非常小,则可视为无效攻击.因此,以目标值的5%,即(0.2±0.01)m为界,若攻击对小球位置的影响小于5%,认为攻击无效,反之认为攻击有效.据此定义攻击有效率(attack efficiency,AE)表示攻击者成功导致系统偏差大于5%的概率.
当检测值超过阈值δ时,检测器触发警报信号.虚警率(FAR)表示攻击无效,而检测器触发警报的概率.漏警率(MAR)表示攻击有效,而检测器没有触发警报的概率.准确率(Accuracy)表示检测器正确触发警报的概率,即在攻击有效时触发警报或在攻击无效时不触发警报的概率.根据攻击是否有效以及检测器是否触发警报,分为以下4种情况:1)正确肯定(true positive,TP):攻击有效,检测器触发警报;2)错误肯定(false positive,FP):攻击有效,检测器没有触发警报;3)错误否定(false negative,FN):攻击无效,检测器触发警报;4)正确否定(true negative,TN):攻击无效,检测器没有触发警报.因此,攻击有效率(AE)、虚警率(FAR)、漏警率(MAR)和准确率(Accuracy)的表达式分别为

由于攻击持续时间较小时,攻击有效率低,随着攻击持续时间的增加,攻击有效率能达到100%.基于1000组攻击测试,统计结果显示攻击持续时间低于0.1 s 时,攻击有效率低于50%,而高于0.35 s时,攻击有效率接近100%.为选定具有较高攻击有效率的攻击持续时间,在(0.1~0.35)s之间,每隔0.05 s设定一个攻击持续时间,每个攻击持续时间的测试为600组,统计不同攻击持续时间的攻击有效率得到图12.
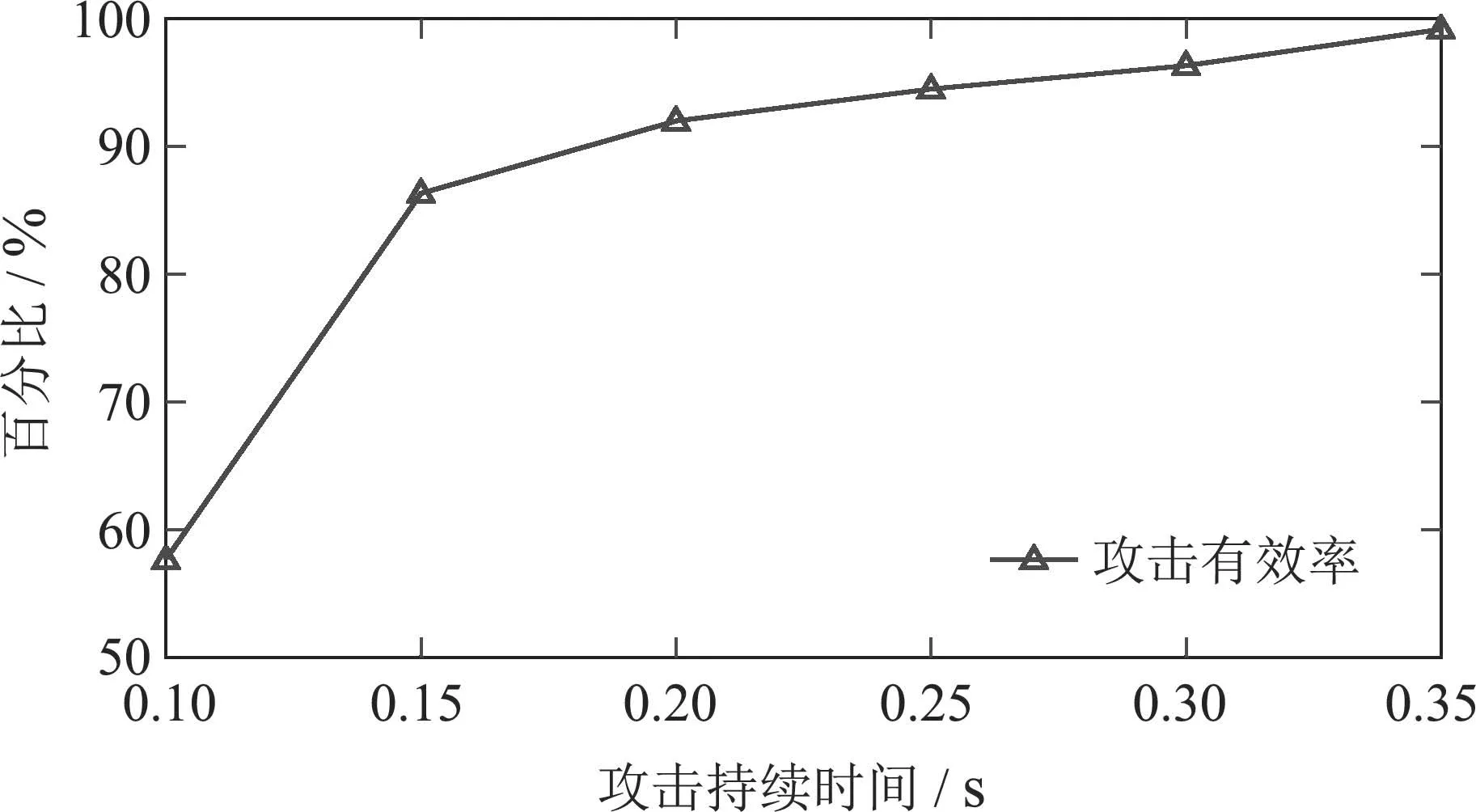
图12 不同攻击持续时间下的攻击有效率Fig.12 Attack efficiency under different attack durations
分析图12可知,攻击有效率随着攻击持续时间的增加而变大,当攻击持续时间高于0.25 s时,攻击有效率大于94.6%.结合攻击者的攻击资源并保证高攻击有效率,假定攻击持续时间为0.3 s,此时的攻击有效率为96.33%.使用两种检测器分别进行攻击检测,得到卡方检测器和欧几里得检测器下的虚警率和漏警率变化曲线分别如图13和图14所示.
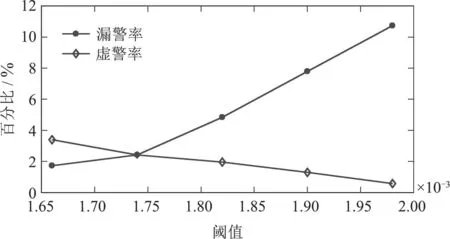
图13 持续0.3 s攻击时,χ2检测器的虚警率和漏警率变化曲线Fig.13 The false alarm rate and the missed alarm rate curve of the chi-square detector during the 0.3 s attack
分析图13可知,随着阈值的增加,卡方检测器的虚警率逐渐减小,漏警率逐渐增加,漏警率的增加幅度比虚警率的减小幅度大,选择等错率为2.42%时对应的值1.74×10−3作为卡方检测器的阈值.同理,分析图14可知,取等错率5.20%对应的值3.16×10−2作为欧几里得检测器的阈值.
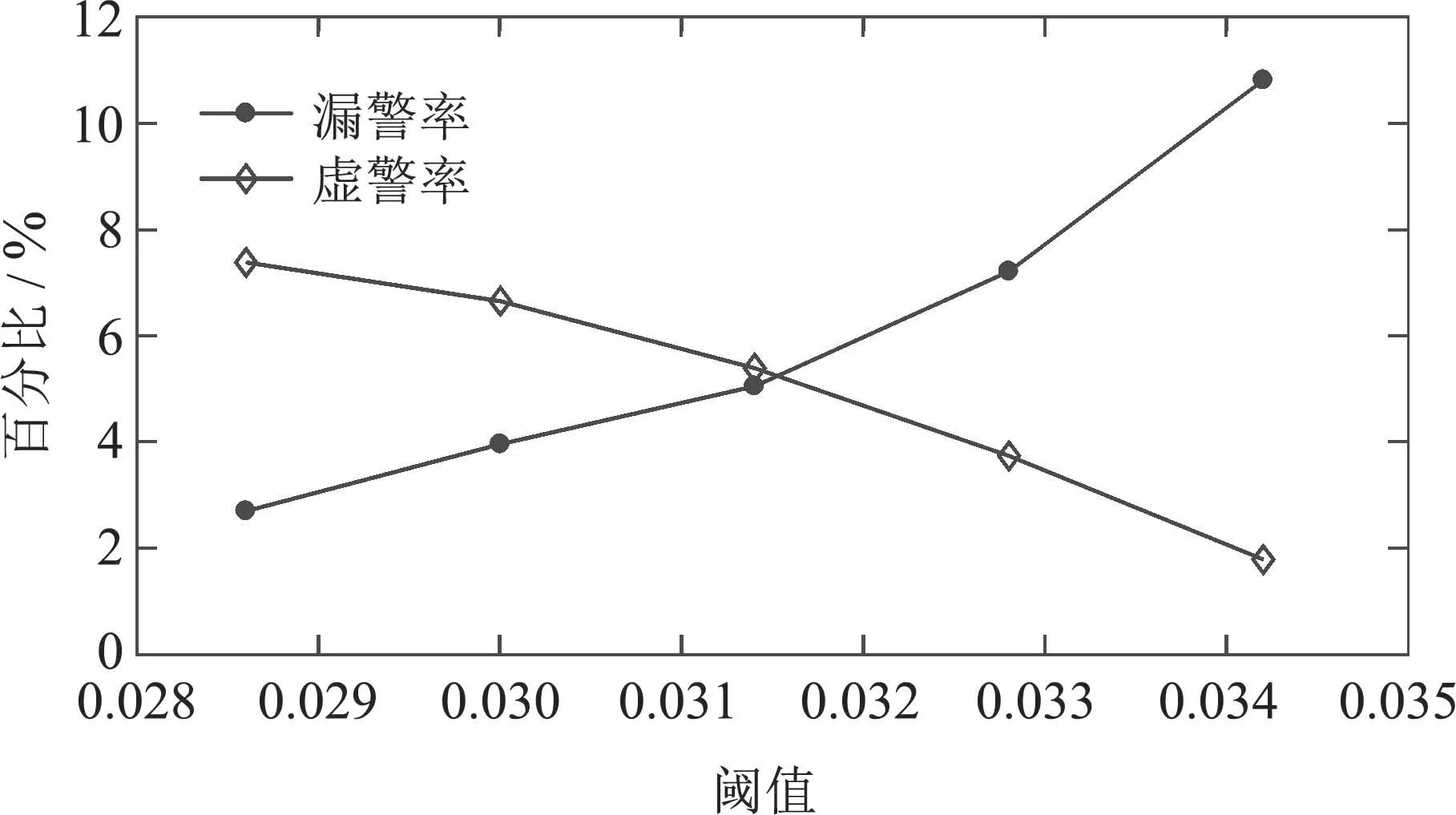
图14 持续0.3 s攻击时,欧几里得检测器的虚警率和漏警率变化曲线Fig.14 The false alarm rate and the missed alarm rate curve of the Euclidean detector during the 0.3 s attack
3.2.4 性能分析
对比分析图13和图14可知,在等错率情况下,χ2检测器的虚警率和漏警率均低于欧几里得检测器.为进一步对比两种检测器的性能,表2列出了0.3 s攻击下不同阈值的检测率和准确率.
由表2数据可知,不同阈值下两种检测器的检测率变化趋势相似,均随着阈值的增加而减小.卡方检测器在选定阈值1.74×10−3下的检测率和准确率分别为97.23%和95.33%,欧几里得检测器器在选定阈值3.16×10−2下的检测率和准确率分别为94.80%和90.83%,对比可知,在检测率和准确率指标上χ2检测器均优于欧几里得检测器.因此,相较于欧几里得检测器,χ2检测器能够更好地检测DoS攻击.

表2 两种检测器在不同阈值下的检测率和准确率Table 2 Detection rate and accuracy of two detectors at different thresholds
4 结语
为了检测ICPS中的DoS攻击问题,本文立足线性时不变控制系统,研究了一种基于反馈控制理论的攻击检测模型.采用卡尔曼滤波和χ2检测器组合的检测方案,卡尔曼滤波器用于去除环境噪声和攻击造成的攻击噪声,并得到测量残差zk;χ2检测器通过测量残差得到检测值g(zk),再与阈值δ进行比较,使用DoS攻击检测判决规则来判断系统是否遭受DoS攻击.为验证所提出的二元假设检验理论和χ2检测器的有效性,以球杆系统为被控对象,采用Simulink/TrueTime进行仿真,仿真结果表明所提出的二元假设检验理论是正确的,结合了卡尔曼滤波器的χ2检测器通过DoS攻击检测判决规则能够有效的用于检测ICPS中的DoS攻击,并通过与欧几里得检测器作对比,凸显了检测模型中χ2检测器的优越性能.
附录:
增益Kk是通过最小化时刻的输出估计误差ek而计算得到的最优卡尔曼增益.最小化误差ek,即最小化ek的二范数的期望E[∥ek∥2],等同于最小化协方差矩阵Pk的迹(主对角元素的和),这样就使得每个被估变量的方差和最小.此外,协方差矩阵Pk为对称矩阵,增益Kk的具体计算过程如下:
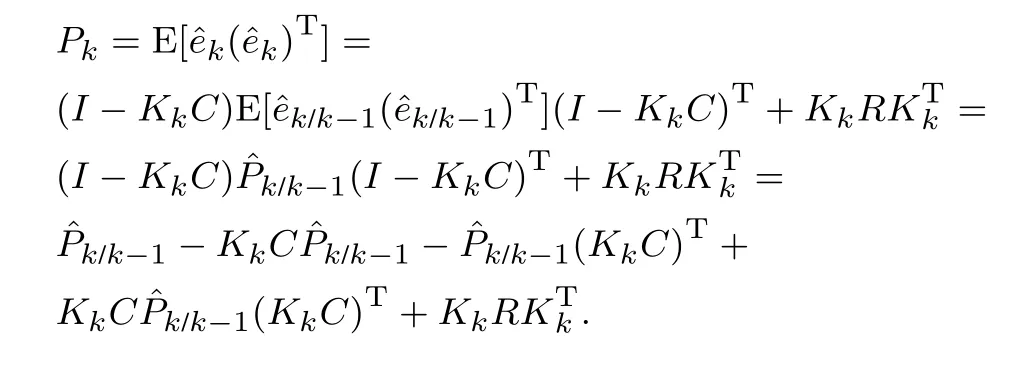
两边取迹可得
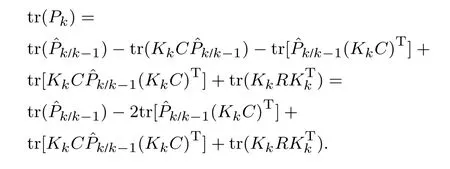
等式两边同时对Kk求导并令结果为0,得
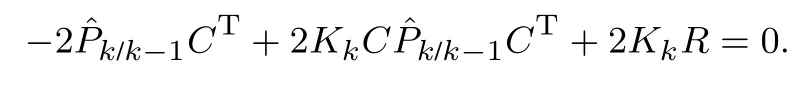
整理得到最优增益