基于时空近邻标准化和局部离群因子的复杂过程故障检测

冯立伟李 元张 成谢彦红

(1.沈阳化工大学数理系,辽宁沈阳 110142;2.沈阳化工大学技术过程故障诊断与安全性研究中心,辽宁沈阳 110142)

1 引言

伴随着现代化学工业产品在生产和生活各领域中广泛应用,如何保证生产过程的安全性和产品的高质量成为一个重要问题.基于数据驱动的故障检测和过程监控技术在化学工业过程中已经得到了广泛的应用.主元分析(principal component analysis,PCA)、偏最小二乘方法和独立元分析是经典的故障检测方法[1–12].它们都采用了统计量T2和SPE对过程进行监控,但这两个统计量都假定数据来源于独立同分布的单模态生产过程.

当过程具有动态特性时,前后时刻样本存在的时序相关性导致数据无法满足独立性的要求,针对此问题,Ku等提出了动态主元分析(dynamic principal component analysis,DPCA)[13].Rato 等[14–15]研究了DPCA中时滞参数选取问题.DPCA通过构造时滞矩阵将不同时刻样本间的时序相关性转化为变量间的相关性,成功消除了时序相关性的影响.但是,DPCA类方法并不适用于多模态过程.

针对过程的非线性和多模态特征,He等提出了基于k近邻的故障检测方法(knearest neighbor rule,kNN),并成功检测出半导体蚀刻工艺过程的大部分故障[16].针对各模态方差不同的多模态过程,冯等提出基于标准距离K近邻方法[17].但是,当过程具有强动态性时,kNN类方法的检测性能显著降低.非线性、多模态过程的另一类监控策略是标准化方法.Ma等提出局部近邻标准化(local neighborhood standardization,NS)的故障检测方法[18–19].冯等提出统计模量和局部近邻标准化的局部离群因子故障检测方法[20].NS类方法将多模态数据融合为单模态数据,但亦没有考虑时序相关性的问题.

Breunig 等提出一种基于局部离群因子(local outlier factor,LOF)的离群点检测方法[21].LOF 使用样本的相对密度来度量其离群程度,可以用来区分故障样本和正常样本,能够实现非线性过程、单模态过程或多模态过程(包括方差显著不同)的故障检测[22–24].Ma等提出马氏距离局部离群因子的故障检测方法[22].刘等提出基于局部密度估计的多模态故障检测方法[23].Zhu等提出多模态批次过程LOF监控,并应用于青霉素发酵过程中[24].但是,上述LOF类方法均未考虑过程动态性的影响.

针对复杂生产过程的非线性、多模态和动态特征,本文提出一种基于时空近邻标准化和局部离群因子(time-space nearest neighborhood standardization and LOF,TSNS–LOF)的故障检测方法,并在数值模拟过程和化工生产过程中进行了检验.

2 局部离群因子方法

LOF方法使用局部离群因子表征样本的离群程度,是一种建立在可达距离基础上的基于相对密度的离群点检测算法,能够对无动态性的非线性、多模态过程进行故障检测.LOF方法计算过程如下:

首先,寻找样本x的前k近邻集,并计算x到每个近邻样本的第k可达距离

其中:dk(x(k))是x和其第k近邻x(k)间的距离,d(x,x(f))是x和其第f近邻x(f)间的距离.

其次,计算样本x的局部可达密度

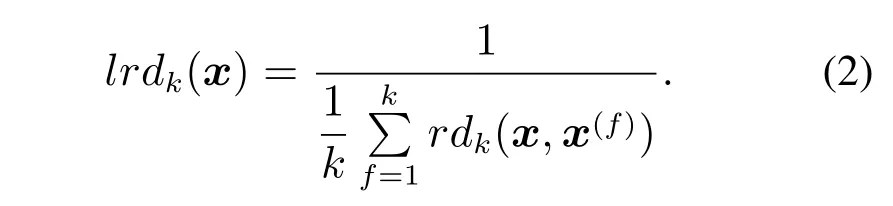
最后,计算样本x的局部离群因子

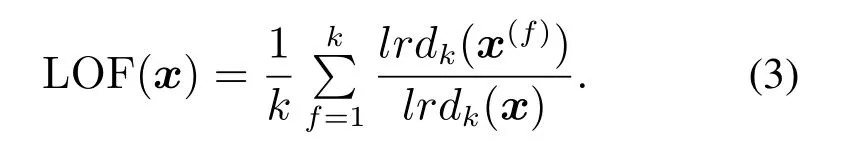
在所有训练样本的LOF值的基础上使用核密度估计等方法确定其所服从的分布,并将其分布的上分位点作为检测模型的控制限.当一个在线样本的LOF值大于控制限时,判定过程发生故障,否则为正常.

在LOF方法中,近邻距离的计算能够消除数据的非线性、多模态特性,使数据集融合为单模态数据;相对密度的计算能够调整数据的疏密程度使各模态数据的方差近似相等.

当过程变量随时间具有显著变化时,其数据中心逐渐漂移且方差逐渐变化,这导致LOF方法对部分故障会出现漏报.使用一个动态非线性的数值模拟过程进行阐述.过程有两个输入变量θ,t和两个输出变量x1,x2,模型如下:

其中:a为过程参数,本文取为0.2,e1,e2为随机噪声.过程正常运行产生500个样本作为建模数据.再次,让过程正常运行,但从2π时刻起在变量t上添加幅值为−4的阶跃型扰动信号,共产生500个样本作为测试数据.所有数据的空间分布见图1(a),正常数据的中心和方差随时间逐渐变化,位于后半阶段的故障样本靠近前半阶段的正常数据.

使用LOF方法对该过程进行故障检测实验,选取近邻个数为4,取97%的置信度,检测结果见图1(b).从图1(a)可看出有大量故障非常接近正常样本导致其可达距离较小,所以其局部离群因子小于正常样本,因此被LOF误报为正常样本.

图1 动态非线性过程监控Fig.1 Monitoring for dynamic and nonlinear process

3 基于时空近邻标准化局部离群因子的故障检测方法

当故障靠近正常样本时,为了避免LOF方法的误报,可以先采用标准化策略对数据进行处理,使故障样本远离正常样本.Ma等[19]提出了NS–LOF方法,使用样本的最近邻样本的近邻集标准化当前样本,再使用LOF方法进行检测.NS–LOF的步骤如下:首先寻找样本x的最近邻样本x(1),其次寻找x(1)的前N近邻样本集,计算此近邻集的均值m(N(x(1)))和标准差s(N(x(1))),最后使用式(5)对x进行标准化:

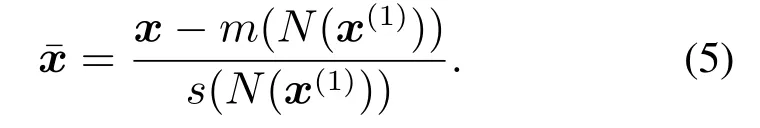
使用NS方法对前一节图1(a)中的过程数据进行处理,选取近邻个数为4,结果见图2(a).由于后半阶段发生的故障样本的最近邻样本处于前半阶段,导致其近邻集也都来自前半阶段样本集,所以该部分故障样本在NS标准化后混入了正常样本,NS标准化出现了错误.因此,所用的近邻样本应来自于样本的相近时刻的正常样本才是合理的,所以本节提出数据处理方法—–时空近邻标准化(TSNS).

首先,在训练集中寻找样本x在时间方向上的前N近邻样本集再寻找在空间方向上的前K近邻样本集=使用式(6)–(7)计算此样本集的均值和标准差,最后使用式(8)将x标准化为标准样本:

图2 TSNS–LOF方法对动态非线性过程的监控Fig.2 Monitoring of TSNS–LOF method in dynamic and nonlinear process

对于正常样本而言,其时间和空间近邻样本都是相似的,经TSNS处理后样本位于坐标原点周围.对于故障样本而言,它离其同时刻的正常样本较远,所以其近邻距离较大,经TSNS处理后,其标准样本离坐标原点较远.总之,TSNS方法能够实现故障与正常样本在空间上的分离.由于TSNS方法使用了相近时刻样本的近邻集,能够避免只使用空间近邻导致的错误.

时空近邻标准化中的两个近邻参数N和K的选取原则:要求训练数据经时空近邻标准化后数据具有最佳的正态性.此时每个样本之间是独立的,也就是没有时序相关性,即消除了过程的动态性.

使用TSNS方法对前一节的数据进行标准化处理,其中N=4,K=5,结果见图2(b).TSNS方法实现了故障样本和正常样本的分离.

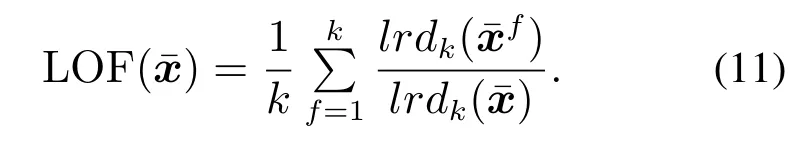
最后,根据训练样本的LOF值使用核密度估计等方法确定其分布,将其分布的相应于置信度α的上分位数作为检测模型的控制限.TSNS–LOF具体计算过程如下:

1)离线建模.

a)采集正常样本组成模型的训练集X,对每个样本xi寻找其时间方向上的前N近邻集N(xi)=,再对N(xi)中的每个样本,寻找其空间方向上前K近邻集

b)使用式(6)–(8)进行对xi进行时空近邻标准化,获得标准样本,组成标准训练集.

d)对全体训练样本的LOFi使用核密度估计方法确定相应于置信度α的检测模型控制限LOFα.

2)在线检测.

a)在X中,寻找在线新样本x在时间方向上的前N近邻集,再对N(x)中的每个样本,查询其空间方向上的前K近邻集

b)使用式(6)–(8)对x进行时空近邻标准化操作,获得标准样本.

d)当LOFx >LOFα时,则判定样本x为故障,否则为正常.

图2(c)为参数k=4时TSNS–LOF方法对前一节所述过程的故障检测结果,检测出全部故障.

4 TE过程故障检测

田纳西–伊斯曼过程(Tennessee–Eastman process)是一个典型的化工联合生产过程.已有大量的过程控制和故障诊断方法[2,6,8,12,15,18,25]将其作为算法的评价测试平台.TE过程主要由反应器、冷凝器、压缩器、分离器和汽提塔等5个操作单元组成[15,18].在生产过程中,4种气态物料A,C,D和E反应生产出两种产品G和H,伴有一种副产品F,另外在进料中还混有少量的惰性气体B[15,18].

TE过程包含12个控制变量,19个连续测量变量和22个成分测量变量[15,18].本文选取全部41个测量变量用于故障检测.过程在模态1(G:H=50:50)下正常运行48 h后,切换到模态3(G:H=90:10)下再运行48 h,前后分别以3 min和6 min为间隔采集数据组成训练集;为了检验TSNS–LOF方法的性能,产生一组测试集:过程在模态1下运行48 h,从8 h至结束引入7类故障,以3 min为采样间隔产生测试数据,故障描述见表1.

表1 TE过程故障描述Table 1 Fault descriptions for TE process

使用PCA,DPCA,kNN,LOF 与TSNS–LOF对TE过程进行监控,并检测故障,所用方法的置信水平均取为97%.图3给出了测试集中故障批次f6的检测图,表2分别给出了所用方法对测试集中全部故障批次的故障检测率和误报率(最后一行).

PCA和DPCA主元个数分别取为9和20[14],DPCA中的时滞参数取为2[14].kNN 的近邻个数k=4.TSNS–LOF 方法的近邻个数N=3,K=4,k=4.从表2可看出所有方法对测试集的故障f1,f2,f3,f4的检测率均较高;PCA,DPCA,kNN和LOF方法对故障f5,f6,f7的检测率较低,而TSNS–LOF方法检测率最高.

Fig.3 测试集中批次f6的故障检测结果Fig.3 Fault detection results for batch f6 in test set

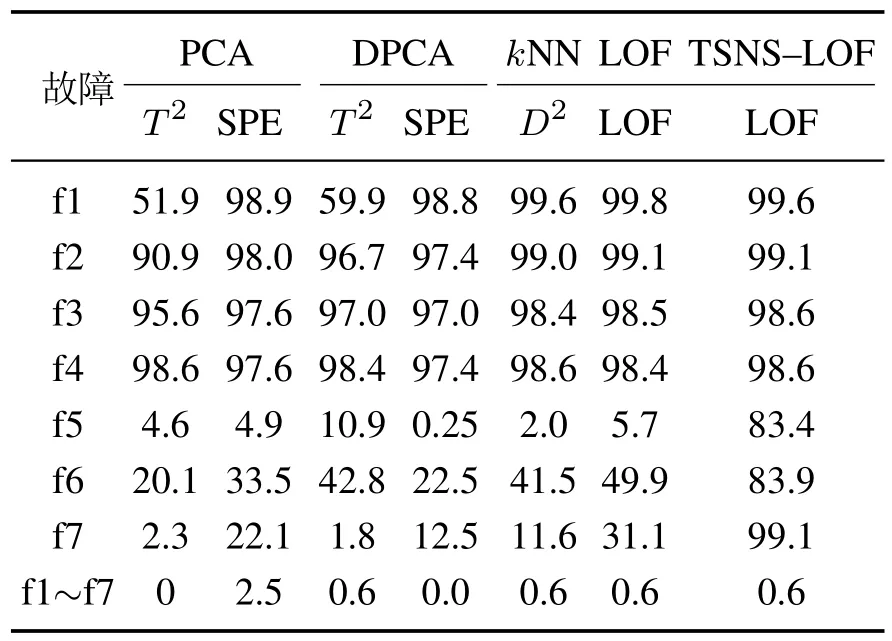
表2 测试集的故障检测率和误报率(%)Table 2 Fault detection rate and false alarm rate of test set(%)

图4(a)给出了正常样本和故障f7的反应器温度和反应器冷凝液出口温度,TE过程正常数据分为两个模态,故障f7位于正常样本周围.PCA,DPCA方法的统计量都要求过程数据服从单模态的多元高斯分布,它们的T2控制限为在各自主元空间内中心在原点的超椭球面.而很多故障位于两个模态数据之间,即比较接近数据中心导致其T2值较小,它们被错误地包含在超椭球面内部,导致误报为正常,所以T2对f5,f6,f7的检测率较低.SPE控制限为残差空间内的超球面,由于大多数故障位于两个模态数据之间,导致其到数据中心的欧式距离较小,也被包含在超球面内部,仍被误报为正常,所以SPE 对f5,f6,f7 的检测率也较低.DPCA方法虽然能够提取过程的动态特性,但是其统计量亦有单模态的多元高斯分布的假设,所以其对多模态过程的部分故障的检测率也比较低.

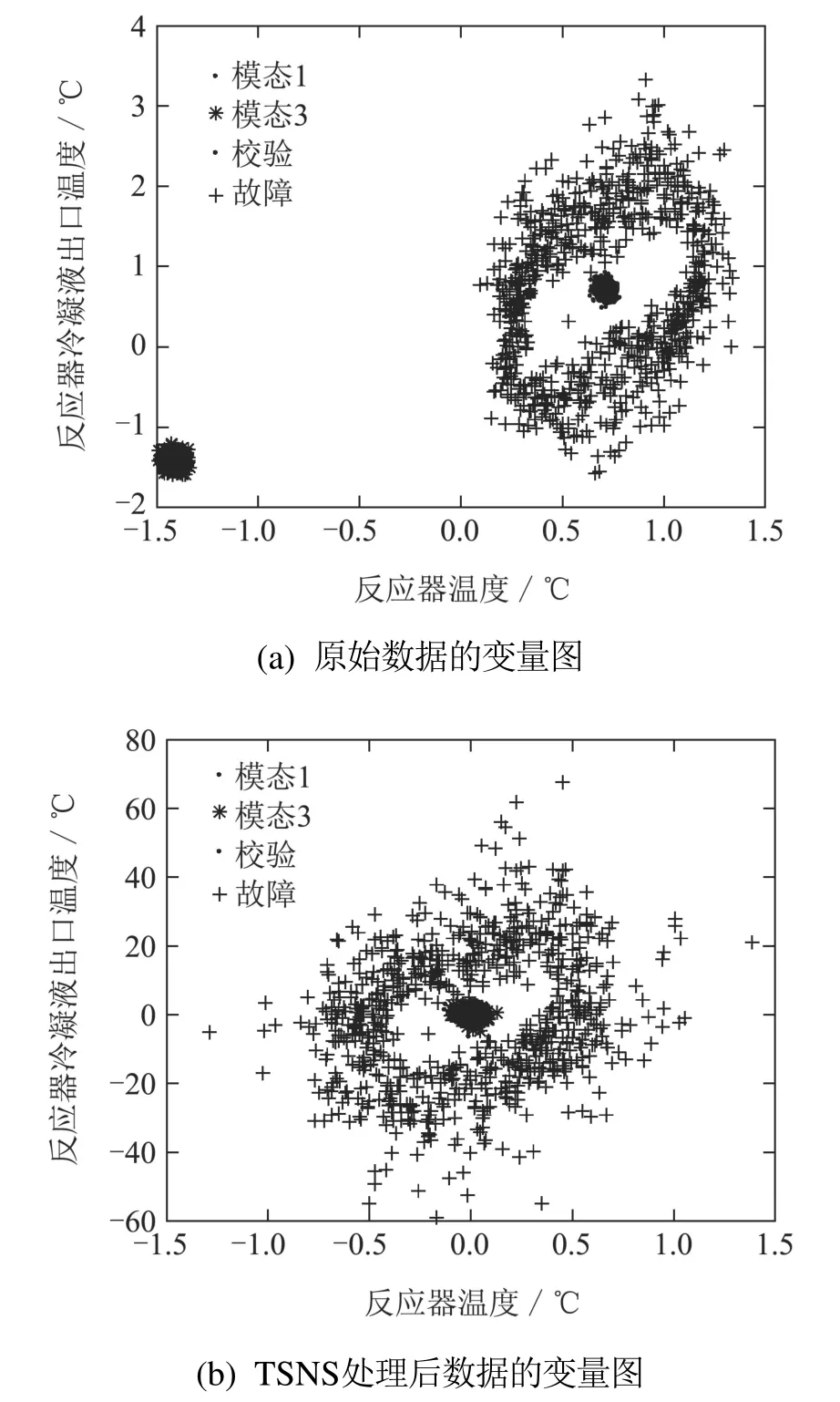
Fig.4 TE过程数据图Fig.4 TE process data diagrams

kNN方法和LOF方法能够对一般的多模态过程进行故障检测.LOF方法能够提取疏密程度信息,所以其对f5,f6,f7的检测率比kNN方法略高.但它们对f5,f6,f7的检测率仍然较低.下面以故障f7的第201个样本分析kNN方法和LOF方法漏报的原因.此样本的故障主要发生在第9个变量(反应器温度)上见图4(a)中方框点.所有训练样本的统计量中变量贡献值的平均值见图5,在其变量贡献值中,虽然第9个变量贡献值高于正常样本的,但是其余变量的贡献较小,导致其变量贡献值之和(即统计量)小于训练样本的,也就低于控制限,所以不能被LOF方法检测出,kNN方法的原因类似.

TSNS–LOF方法使用正确时刻的近邻集信息将数据标准化为单模态数据见图4(b),同时其避免了故障样本标准化出错的问题,所以TSNS–LOF方法的检测率最高且检测比较及时,见图3(e)和表2.

Fig.5 LOF中变量贡献图Fig.5 Contribution diagram of variables in LOF

5 结论

通过数值模拟过程分析了LOF在动态过程故障检测中存在的不足.针对复杂过程的非线性、动态性和多模态的特点,提出了TSNS–LOF的故障检测方法.TSNS克服了非线性、动态性和多中心的不利影响.将TSNS–LOF 应用于TE 过程故障检测过程中,并与PCA,DPCA,kNN,LOF方法进行比较.实验结果表明TSNS–LOF对动态性或多模态过程故障具有较高的检测能力.