基于四阶累积分析的工业大肠杆菌制备过程故障诊断

常 鹏乔俊飞张祥宇王 普

(1.北京工业大学信息学部,北京 100124;2.北京工业大学计算智能和智能系统北京市重点实验室,北京 100124;3.北京工业大学数字社区教育部工程研究中心,北京 100124)

1 引言

多元统计技术已经广泛应用到间歇过程的过程监测中,因其只需要生产过程数据进行统计建模,无需考虑间歇生产过程复杂的机理特性,在工业界和学术界得到了卓有成效的应用,其中针对非线性问题具有代表性的就是多向核主成分分析[1–4](multiway kernel principal component analysis,MKPCA),多项核偏最小二乘方法[5–10](multiway kernel partial least square,MKPLS).尽管MKPCA/MKPLS及其扩展方法在过程故障检测得到了广泛应用,但其要达到好的监测的效果必须是假设生产过程属于高斯分布,在进行过程特征提取时,仅仅考虑低阶统计信息,未考虑过程数据的高阶统计量信息,会造成特征提取的不充分[10–12].这是因为高斯过程的二阶以上统计信息为零,而实际的间歇工业过程往往同时具有非线性和非高斯性,用以上方法对非高斯过程进行监测势必导致监测模型存在大量的报警问题,甚至导致失效性.针对间歇生产过程数据普遍具有非线性和非高斯性共存的问题,近些年来,基于多向核独立元分析[10–18](multiway kernle independent component analysis,MKICA)的监测方法逐渐发展了起来.其具体核心算法是将原始数据用KPCA进行白化处理,解决数据的非线性,得到不相关的得分矩阵后进行ICA分解提取过程的独立成分.但是KPCA在进行白化处理时其实质是在特征提取,而其特征提取的依据是方差.然而间歇过程具有明显的阶段簇结构特征[19],以本文采用的对象,工业重组大肠杆菌制备白介素–2为例,其生产过程按照微生物机理分为无补料菌种培养阶段、菌种的补料快速生长阶段、诱导产物合成阶段,具有明显的多阶段特性[20].为解决上述问题,常鹏等人[20]提出了一种基于MKECA[21–22]白化的MKEICA方法.该方法利用MKECA进行特征提取时能够保留数据的簇结构的阶段特征,之后在核熵空间建立ICA监测模型用于生产过程的监控.但是以上MKICA/MKEICA监测方法在进行过程监测时,所使用的监测统计量I2和SPE是低阶统计量,只能监测生产过程的低阶统计信息,不能监测生产过程的高阶统计的信息,如生产过程中产生的故障具有明显的高阶统计信息时其将无能为力,而实际的生产过程往往具有高阶统计信息[23–25].而文献[24–30]指出,非高斯信息需要高阶矩(大于二阶矩)来分析,并强调第四阶矩含有明显的非高斯信息.为此本文将MKEICA[20]作为基础的建模监测模型,构建四阶累积监控统计量用于过程监控,当监测到故障时采用本文提出的故障诊断方法对故障变量进行追溯.采用高阶累积分析建模时具有以下3点优势:

1)高斯过程的高阶累积量为零,而非高斯过程的高阶累积量不全为零.因此,高阶累积量可用于高斯噪声中非高斯信号的提取.

2)高阶累积量不仅具有信号的幅值信息,同时具有相位信息.

3)高阶累积量可用于监测和描述系统的非线性.

综上本文提出的方法与传统MKICA方法同时用于工业大肠杆菌制备现场验证其算法的有效性,当监测到生产过程出现故障时,对故障变量进行追溯,定位故障源,验证该故障诊断方法的实用性.

2 四阶累积量分析

四阶累积量(forth-order cumulants analysis,FCA)是随机非高斯特性的参数矩估计[23–25],对于一个零均值变量k维随机向量X=[x1x2··· xk],若其联合概率密度函数为f(x1,x2,···,xk),则其第一特征函数定义为

式中:ω=[ω1ω2··· ωk],E{·}表示数学期望,j=X的第2特征函数又称为累积量生成函数定义为

式中ln表示自然对数.分别对ϕx和ψx(ω)求关于ω的r=r1+r2+···+rk阶偏导,同时令[ω1=ω2=···=ωk=0],即可得到X的r阶矩mr1···rk与r阶累积量cr1···rk

式中mom{·},cum{·}分别是矩和累积量的符号.实际应用中常取r1=r2=···=rk=1,对于零均值的k阶平稳随机信号x(h),令x1=x(h),x2=x(t+h1),···,xk=x(t+hk−1),h为时间滞后.则该信号的k阶矩和k阶累积量分别定义为

其中k阶矩mkx(h1,h2,···,hk−1)可由式(2)求得,结果为

k阶累积量ckx(h1,h2,···,hk−1)由矩与累积量转换关系求出,首先引入符号集的概念,对于k个随机变量的集合{x1,x2,···,xk},其符号集合为I={1,2,···,k}对I进行无连接的非空分割得到q个子集合记作Ip,要求I=∪Ip,Ip非空且是无序组合,各Ip无交集.累积量–矩转换公式(C–M公式)为

对于均值为零的随机信号xk,其四阶累积量为

其中:E表示期望;Rx表示信号x(t)自相关系数;令h1=1,h2=2,h3=3是滞后时间.本文的数据经ICA处理后具有独立性,这里Rx恒为零,故四阶累积量可改写为

3 基于四阶累积量分析的过程故障诊断

3.1 四阶累积监测统计量的构建

核函数选择间歇过程监测领域最常见的径向基函数(radial basis function,RBF)核[1–23],具体如下式所示:

本文利用核熵值的累积贡献率来进行核熵个数的选择,累积核熵贡献率定义如下所示[20]:

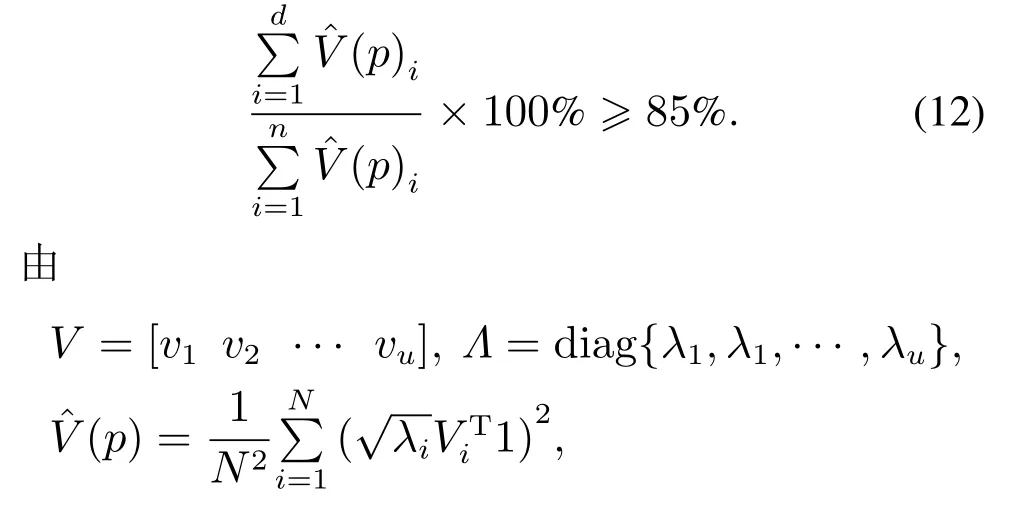
则MKECA负载矩阵为

白化矩阵为

MKECA得分为

对于一个新时刻的数据向量xnew,其对应的核熵向量为

则新的KECA得分为

新的白化得分为

根据s的非高斯性大小这里采用独立元得分累积贡献最大的几个独立成分sd,与其对应的B矩阵的列组成矩阵Bd,其独立成分为.

定义新的监测统计量HS和HE并计算其控制线,将整个过程分为主导独立成分和模型预测误差两部分,在采样i处,第p个主导独立成分sd的样本四阶累积量为

其中:wp是解混矩阵Wd的第p个向量,p=1,2,···,d.为了监测全部主导独立成分的四阶累积量,第1个监测指标定义为

在采样i处,非高斯模型对第q个变量的预测误差的样本三阶累积量为

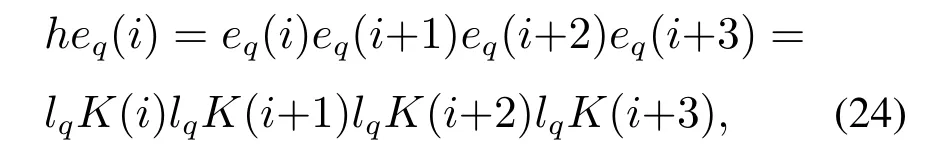
其中lq是L的第q行,q=1,2,···,m,HCA的第2个监测指标定义为

至此,离线阶段的模型建立完毕,这里需要用核密度估计[26–28]分别计算监测统计量HS和HE的置信区间用于在线监测.

3.2 在线监测

对于在线监测,新时刻数据的监测统计量定义如下式所示:

3.3 故障诊断

采用RBF核函数计算核矩阵[1–25],假设存在向量v=[v1v2··· vm]T,i=1,2,···,m,核函数对于第i个变量vi的偏导可用下式计算:

其中xj,i为第j个样本的第i个变量.因此,第i个变量对核向量第j个元素的贡献为求两个核函数乘积的偏导

对于在线监测,根据变量对角贡献[11],核向量的第j个元素对HS的贡献为

进一步,hsnew,p中第i个变量对HS的贡献为

按照上述方法求出核向量第j个元素对HE的贡献.可以采用变量贡献分析进行故障诊断.对于一个监测指标,变量对该指标的贡献由下式定义:

式中:

表示第j个变量对HS的贡献,cmhsp,j为第j个变量对hsp的贡献为

进一步,henew,p中第i个变量对HE的贡献为按照HS的分解方法

表示第j个变量对HE的贡献.cmheq,j为第j个变量对heq的贡献,如下式所示:

以上推导了基于核的四阶累积量监测统计量贡献值,当过程监测模型发现有异常情况时,可用此故障诊断方法对故障变量进行追溯.

4 算法实际工业验证

这里实验的主要目的是证明下列观点:1)基于阶段的过程数据是非线性、非高斯性、多阶段共存的,不是单一存在的;2)基于四阶累积监测统计量的故障监测方法具备有效的故障监测能力;3)基于四阶累积监测统计量的故障诊断方法具备故障定位的能力.本文实验的数据取自北京某微生物制药公司的基因重组大肠杆菌外源蛋白表达制备白介素–2.生产发酵过程采用Sartorius BIOSTAT BDL 15L发酵罐,如图1所示.选择6个主要过程变量来综合表征菌体生长及外源蛋白表达的状况,如表1所示.选取35个正常批次作为离线建模数据.对过程变量数据进行正态检验结果如图2所示,如果数据服从正态分布,则图2中数据点击图中蓝色‘+’应该近似为一条直线,即图中红线附近,变量1至变量6都具有非高斯特性.此外,为了验证模型的有效性,引入两种类型的故障如表2所示.

表1 大肠杆菌发酵过程可检测变量Table 1 The measuring parameters in Escherichia coli fermentation processes

表2 工厂过程故障类型Table 2 Fault types introduced in process

4.1 监测结果与讨论

针对表2中的故障1的监测结果如图3所示,两种方法的监测统计量在故障发生的时刻第一时间都超出控制限,但是从图3(a)可以看出,I2监测图在正常阶段存在故障的错误报警现象,如采样点2附近、采样点15附近,SPE监测图存在故障的误报警,如采样点1到3附近,采样点6附近、采样点11附近,从图3(b)可以看出本文所提监控方法的统计量HS和HE监测图不存在故障的漏报警和误报警现象,表现出可靠的过程监测能力,当监测到生产过程存在异常情况时,采用本文所提的故障诊断方法对其进行故障诊断,这里选择25 h进行故障诊断.

图1 大肠杆菌发酵制备系统原理示意图Fig.1 Schematic of fermentation equipment and control system

图2 6个过程变量正态分布检验Fig.2 6 process variables of normal distribution test

针对表2中的故障2的监测结果如图4所示,MKICA的I2监测图在28采样点附近超出控制限,SPE监测统计量在36采样点附近超出监测控制限,基本失去了对此故障的发现能力.而本文所提监控方法的统计量HS在16采样点附近超出控制限,HE监测图在18采样点附近超出控制限,体现了高效的故障监测识别能力,并且不存在故障的误报警和漏报警.

图3 比较两种方法在工业发酵过程故障批次1的监测结果Fig.3 Monitoring results using two methods for industry fault batch 1

采用本文故障诊断方法,选择发现故障后的稳定采样点对其进行故障诊断,选择了第26个采样点.

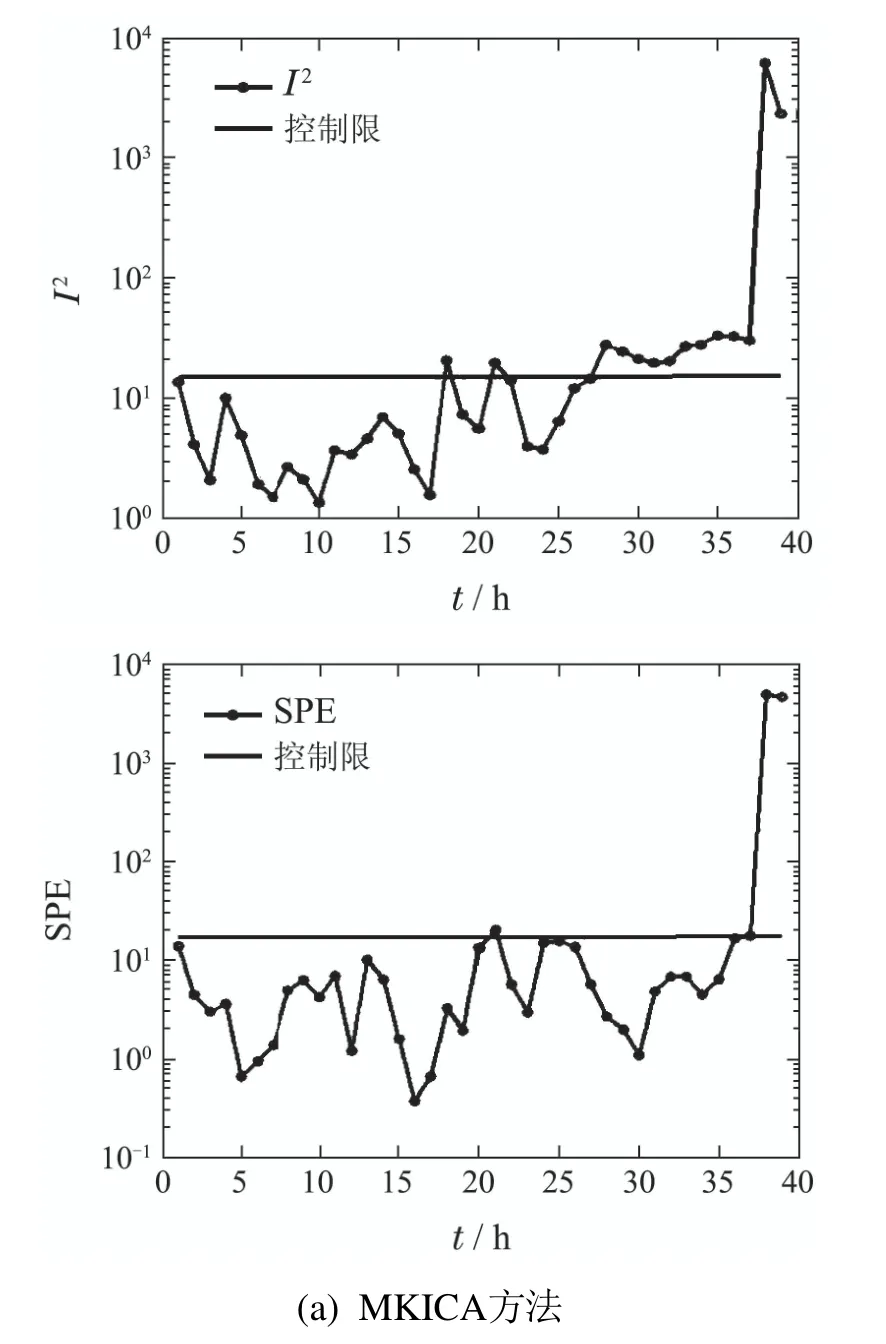
图4 比较两种方法在工业发酵过程故障批次2的监测结果Fig.4 Monitoring results using two methods for industry fault batch 2

针对故障1的故障诊断如图5(a)所示,变量3为故障变量,结合表1–2进行分析可知,可以准确识别故障源.如图5(b)所示,变量5对监测统计量的贡献最大,结合由表1–2进行分析可知,该方法可以准确识别该故障.

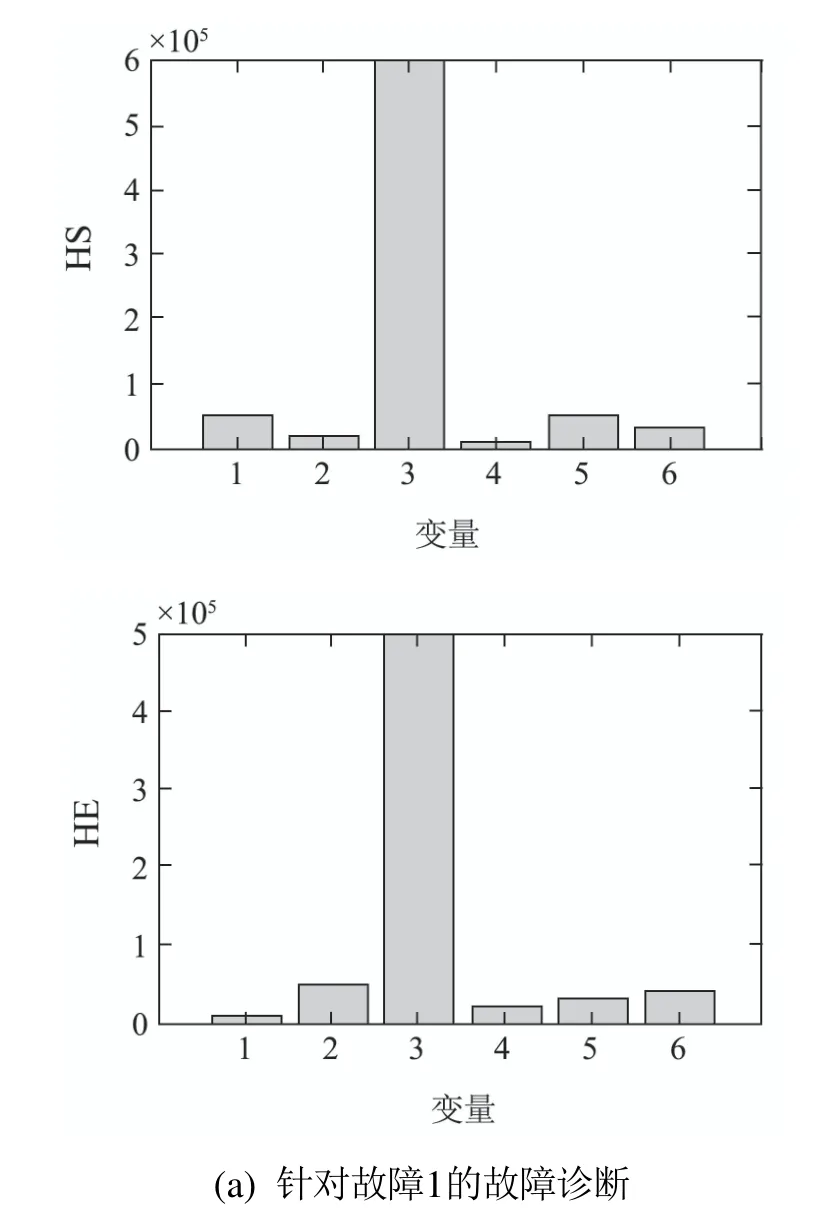
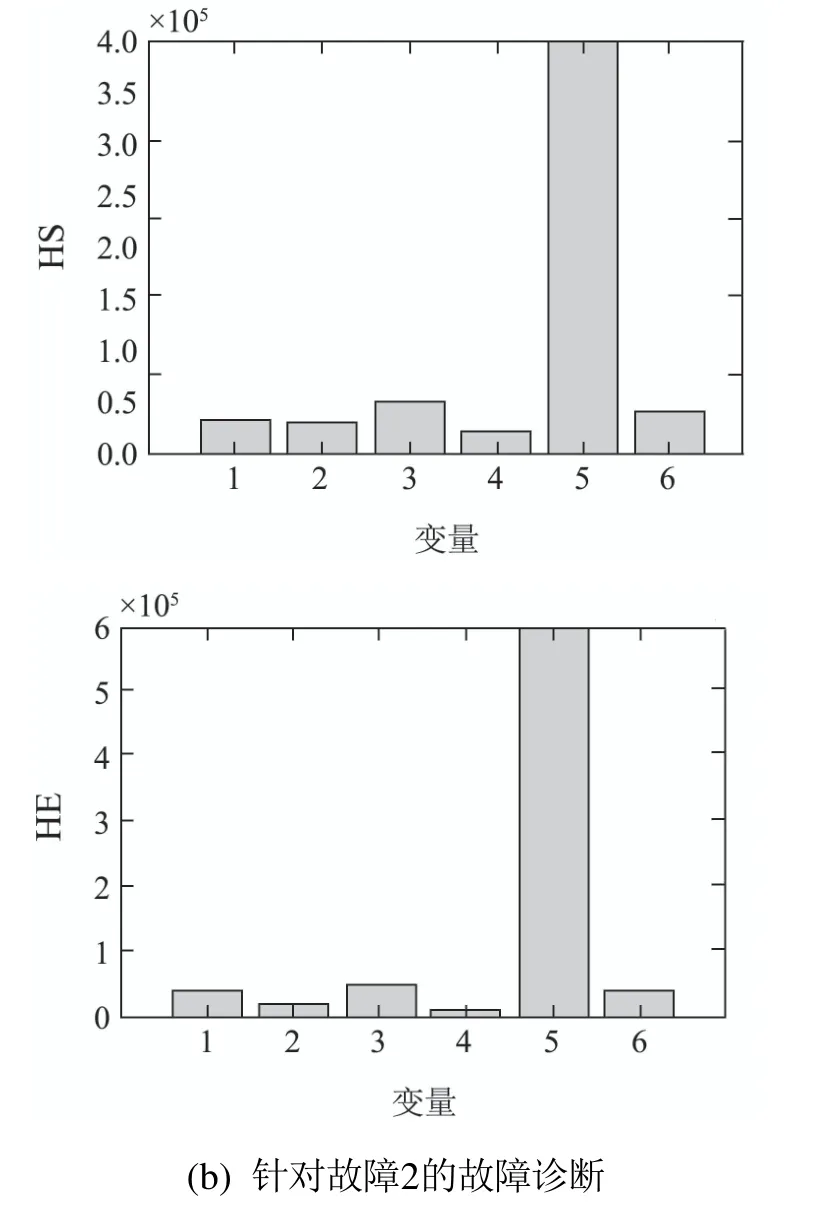
图5 故障诊断Fig.5 Fault diagnosis

通过以上分析,得出FCA监测模型优于MKICA的监测模型.

5 结论

针对工业重组大肠杆菌外源蛋白表达制备白介素-2的数据同时具有非线性、多阶段、非高斯性的特点,同时为了解决传统监测模型难于进行故障监测以及故障源定位的难题,提出基于FCA的过程监测方法.该方法首先利用MKEICA代替传统MKICA监测模型在进行数据特征提取时可以更好保持原始的数据的簇结构阶段信息,其次针对传统MKICA监测方法所构建的监测统计量为二阶统计量的不足,提出了四阶累积量的监测统计量用于过程监测,旨在克服传统统计量在监测时存在较高误报和漏报的问题,此外,本文还推导了基于FCA方法的故障源定位.通过对工业制备大肠杆菌发酵过程的实际应用,表明本文方法与传统MKICA方法相比,不仅能有效提高监控系统发现故障的能力,并且还可以利用本文提出的故障诊断方法准确识别故障源,为间歇过程监测提供一种可行的解决方案,具有一定的实用价值.