基于多数据集动态潜变量的在线性能分级评估方法

曹晨鑫,王 昕,王振雷

(1.华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237;2.上海交通大学电工与电子实验教学中心,上海 200240)

1 引言

由于现代工业过程的复杂程度较高,控制系统的运行条件在不断变化.在控制器工作的初期,控制系统具有良好的运行状态,但是由于操作点变化、仪表失准、执行机构老化缺少维护等各种因素的影响,控制器会发生各种性能下降的情况,逐渐低于理想运行状态.控制性能下降将导致工业产品质量下降、过程操作成本增加和产品利润降低等问题.因此设计一个自动高效的控制性能评估策略,对过程效率的提升和企业经济收益的增加至关重要.

Harris于1989年提出基于最小方差原理的性能评估指标[1].初期的研究重点为单输入单输出过程基于最小方差控制基准的回路性能评估[2].随着现代工业的发展,性能评估拓展到更复杂的多变量控制系统,过程时滞在多变量控制性能评估中起重要作用[3].Huang等提出一种利用闭环操作数据预估单位关联矩阵的方法,其采用单一关联获取最小方差控制基准[4–5].但是关联矩阵的计算通常需要过程模型或至少前几个Markov参数.

针对需要先验知识的问题,Desborough和Huang研究提出基于数据的单变量系统性能评估[6],但是不适用于多变量过程.文献[7–8]提出多输入多输出系统数据驱动的协方差基准,其采用用户选择的典型操作数据避免先验过程知识,提出基于协方差指标评估监测时期整体控制性能的方法,评估的结果是相对于基准数据.文献[9]针对不同稳态性能存在不同过程变化信息的问题,提出一种基于过程变化相似性的在线评估方法,首先依据实际性能指标将过程训练数据划分为几个性能等级,然后采用主元分析(principal component analysis,PCA)提取每个性能级的主要变化信息,依据在线数据与每个性能级训练数据的相似性评估过程性能.但处理包含性能不相关的过程变化的过程数据,基于PCA的评估方法不具备良好的抗干扰能力和敏感性.文献[10]采用综合子空间分解的方法分析各个模态相对于参考模态的变化.通过将各个模态分解为3 个不同的系统子空间和1个残差子空间,对不同的变化部分分别建立模型,定义不同的在线监测统计信息,以识别各个模态所属关系和监测故障状态.此不同模态之间的相关分析方法更注重不同模态之间变量相关性的变化而不是变量相关性的相似程度.文献[11]采用典型相关分析的潜结构建模方法对过程与质量故障进行并发监测与诊断.文献[12]采用全潜结构映射(total projection to latent structures,T–PLS)算法[13–14],以综合经济效益为引导,有效地提取过程数据中的性能相关变化.Liu等采用分层多块的全潜结构映射方法应用于全流程过程性能评估领域[15].但在流程工业过程中综合经济效益和输入数据之间存在一个生产周期或统计时间的延迟,因此在使用T–PLS算法之前需要凭借大量的工作经验对数据与综合经济效益重新排列,工作量是庞大的.文献[16]采用多数据集主元分析(multiset principal component analysis,MSPCA)方法[17]提取多性能级训练数据集合的公共基向量,然后剔除训练数据和在线数据中性能无关的共有过程变化,保留性能相关的特有过程变化.利用欧式距离计算在线数据与各性能级训练数据的相似性,从而进行性能评估.但该方法将性能相近的样本过程数据对应同一个性能标签,增加了评估模型的非线性与不确定性干扰,并且静态PCA模型适用于被测变量为独立正态分布的离散制造过程,不适用于动态的连续过程.动态多变量过程的动态因素难以提取,采用线性方法计算工况多变的动态工业过程数据的相似度难以实现准确评估的目的.

因此本文提出一种基于多数据集动态潜变量分析(multiset dynamic latent variables,MSDLV)的在线性能分级评估方法,首先采用MSDLV算法提取数据集稳态性能级之间性能不相关的变化,剔除公共子空间,保留性能相关的特有变化,并采用DLV[18–21]方法去除特有变化部分过程噪声提取整个采样数据集合的动态潜变量,充分考虑了动态过程的自相关性.然后建立动态潜变量与性能标签之间的非线性离散模型,在线评估时,以滑动数据窗口为评估单元,将提取的测试数据动态特征输入到训练好的神经网络模型中,输出预测值为测试数据与各稳态性能级之间的相似度.同时,定义一个变遗忘因子的过渡性能角系数,以此监控当前过程处于稳态性能等级还是稳态性能之间的过渡状态.最后将MSDLV方法应用到乙烯裂解过程中,通过与MSPCA方法对比,验证该方法在动态过程性能评估中具有良好的效果.

2 多数据集动态潜变量方法

MSDLV方法适用于分析连续多个动态数据集中共有的变量关系,其基本原理是通过提取多个动态数据集之间的公共基向量,分离出数据集的共有变化,将多个动态数据集的特有变化保留,从而增强数据集之间区分度.采用动态潜变量方法提取数据集特有变化的明确动态相关的潜在因素,多数据集动态潜变量模型构造的新的结构可以提升动态数据模型的质量并且提高动态过程性能评估的准确度.

2.1 数据集公共基向量的提取

假设数据集数量为C个,第i个数据集可定义为Xi=[xi,1xi,2··· xi,Ni]T∈RNi×J,i=1,2,···,C,式中Ni和J是Xi的样本个数和过程变量个数.对于每个数据集定义一个代表Xi的子基向量,定义如下:

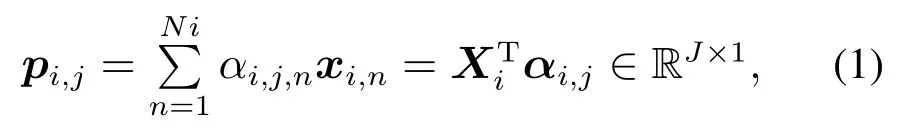
式中αi,j=[αi,j,1··· αi,j,Ni]T为Xi与pi,j之间的线性相关系数.

为了衡量连续多个集合之间的交互关系,引入一个公共基向量pg∈RJ×1,公共基向量与C个动态数据集的子基向量都相近的可能性最大,由此一个受限优化问题可以被描述为

可构造一个Lagrange函数解决上述受限优化问题,Lagrange函数如下:

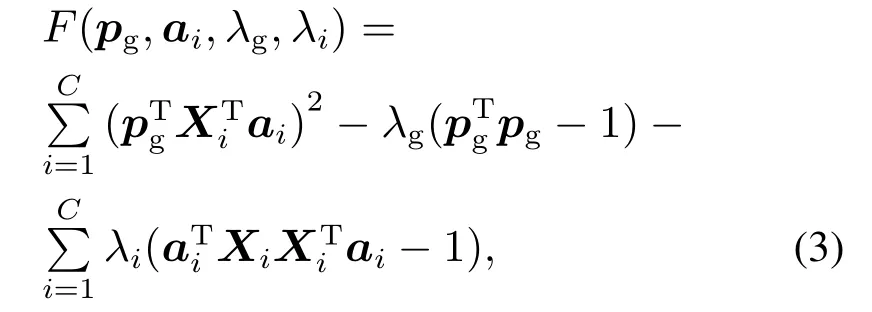
式中λg和λi为常量.基于文献[17]提出的多组变量相关性的两步基向量提取策略,问题(2)最终可被化简成不带约束优化问题:

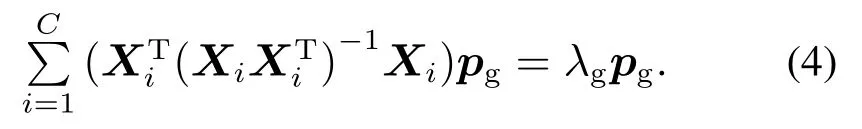
由式(4)可知,最大特征值对应的特征向量即为第1个公共基向量,降序排列的特征值对应的特征向量均与前一个正交,由此可给出不同公共基向量均正交.然而,由于,不能直接对数据集Xi进行特征值分解.文献[17]提出采用不同的损失函数和限制条件分两步提取公共基向量.

第1步将相关系数向量设置为单位长度,建立子基向量和公共基向量之间的协方差信息模型如下:

可构建Lagrange函数将式(5)转化为一个标准代数问题式(6),并且通过计算该标准代数问题得到子基向量:

但是,通过式(5)协方差最大化计算得到的子基向量不一定和公共基向量存在强相关性,因此大的协方差可能是由子基向量大的方差造成的.

第2步使用第1步求得的每个数据集的子基向量代替式(4)的原始数据空间,从而保证了矩阵的可逆性.经过简化步骤可将式(4)转化为

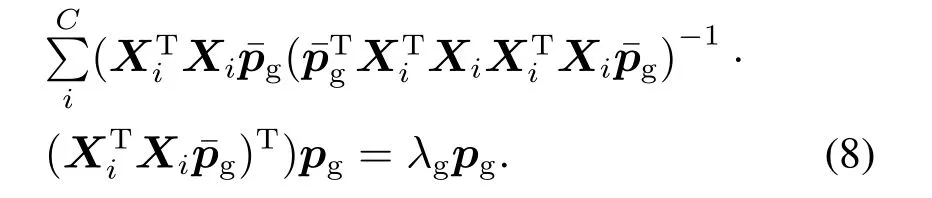
通过计算上式可得到公共基向量pg和公共子空间Pg=[pg,1pg,2··· pg,A]∈RJ×A,公共子空间包含了各数据集潜在的公共信息,基向量的个数为A,由此,可以提取每个数据集的公共子空间.

通常,性能不相关变化包括共有变量关系和共有变化幅值两类,必须将各数据集沿着公共基向量方向的变量关系相等但变化幅值不等的基向量从Pg中剔除.图1是数据集在两个基向量方向上的变化示意图,依据相对变化分析的方法[22],得到数据集X1和X2沿pg,1方向的变化幅值近似相等,但沿pg,2方向的变化幅值差异较大,因此,pg,2不是真正的公共基向量,需要剔除pg,2.

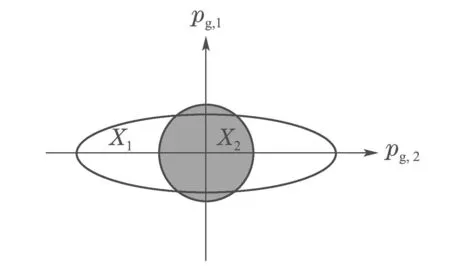
图1 不同的基向量方向上的幅值示意图Fig.1 Schematic of the amplitude along different basis vectors

为实现筛选Pg,Xi沿pg,a(a=1,2,···,A)方向的变化计算如下:

无穷范数∥ti,a∥∞可以表征ti,a的幅值,如果∥t1,a∥∞,∥t2,a∥∞,···,∥tC,a∥∞近似相等,则认为基向量pg,a为真正的公共基向量,判断步骤如下:

1)定义a=1,公共基向量为空,,定义松弛因子δ;

3)当1−δ≤amplitude-ratio[i],i=1,2,···,C −1 ≤1+δ,令,其中:pg,(2)··· pg,(ˆA)];为真正的公共基向量;δ为松弛因子,可通过交叉验证测试得出.

综上,每个稳态性能级的数据集可被分解成如下形式:

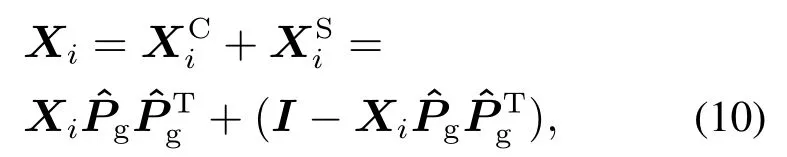
上式中:i=1,2,···,C,是性能不相关的过程变化,对区分数据集的过程性能不起作用;代表性能相关的过程变化,在数据集的性能评估中起重要作用.

2.2 动态潜变量

动态多变量过程中,过程变量不同时刻的数据值相互联系,因此变量表现出明显的自相关性.动态潜变量模型可以有效的区分数据集的动态关系和静态关系,所以有不会忽略评估细小性能变化的灵敏度,并且此方法依据自相关性提取出动态因素.

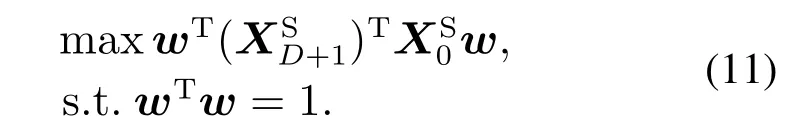
式(11)目标为搜寻带有D+1延迟的最大自协方差的方向,如果缺乏先验知识,通常在延迟为1即D=0的时候获取最大自协方差.假定随着延迟时间增加,自协方差将逐渐消失.因为xSk是正常过程的停滞的时间序列特有变化,这是一个合理的假设.

利用Lagrange乘子构建不带约束的目标函数:

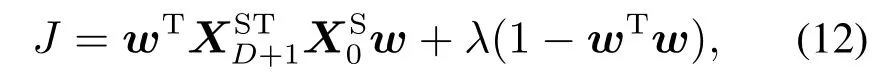
对上式求w的导数:

因为wTw=1,w是下述特征向量问题的解:

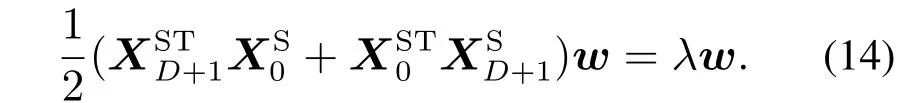
式(13)中最大特征值λmax对应的特征向量是带约束的目标函数式(11)的最优解.如果算式(11)中的协方差为负数,应该求最小值.最终是为了搜索式(14)特征值绝对值最大的|λ|max对应的特征向量.然后,动态得分向量可被描述为

接着，负荷向量p可被定义为

与动态因素不相关的剩余部分为

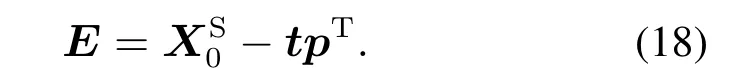
不同于静态PCA,动态主要成分是根据自协方差的程度提取的.求得的剩余部分残留非常小的自协方差,对应的趋向于0.整个过程可总结如下:

方法1(自相关PCA)

1)定义i=1,.

自相关PCA方法类似于传统的偏最小二乘的程序,因此依据相似于PLS的自相关算法,可以描述X空间结构.定义W=[w1w2··· wL],P=[p1p2··· pL],R=W(PTW)−1,得到

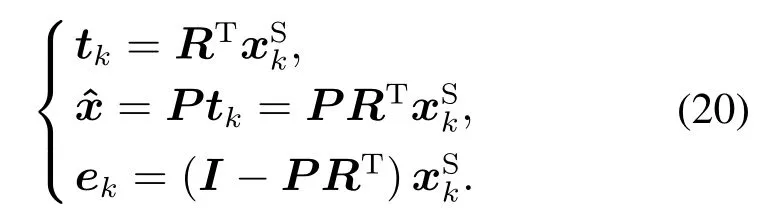
利用方法1,可以确保ek的自协方差趋向于0或等于0,此方法适合提取动态过程数据的动态特性.

定义E=[e1e2··· en]T,E代表过程数据中静态变化.利用自相关PCA方法构建数据XS的外部模型并提取动态潜变量,如式(19)所示.建立一个标准来确定主要动态成分的数量.数据空间X性能相关的过程变化XS的分解式如下:

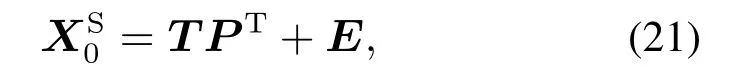
DLV模型着重于将过程的动态变量映射到一个低维的潜在空间,这有利于动态过程的性能评估.

3 性能级数据离线建模

3.1 性能相关变化提取

在工业过程中,根据专家经验和过程的先验知识可以容易地将建模数据划分为不同的性能等级,划分的方法如下:

1)根据过程的运行状态将历史数据中性能稳定并且区分度高的连续数据段分离出来;

2)参考过程生产周期,根据后续的数据处理和生产经验,将每一个数据段的平均性能一一标识出来;

3)依据标识性能大小,将数据划分成不同性能等级的C个数据集,如当C=3时,各数据集代表的经济性能依次为最优、一般、较差.尽管不同性能数据集的过程变化是不同的,但是由于数据来自同一生产过程和随机扰动的存在,它们之间仍然存在相似性、共有信息和明显的自相关性.每个稳态性能级内的数据包含的过程变化包括两部分:一、本性能级数据特有的过程变化;二、各性能级数据共有的过程变化.其中,特有部分是用于区分不同性能等级的重要特征,共有部分作为性能不相关的变化反而会干扰实际过程操作性能的判断.

为了提高在线性能评估的精度,首先采用两步的MSDLV算法将不同离线性能级数据集中共有的变量关系以公共基向量的形式提取出来.假设生产过程的非故障数据划分为C个稳态性能等级,将每个性能级的训练数据进行零均值和单位方差标准化,得到数据集合Xi,i=1,2,···,C.然后,采用MSDLV算法计算得到A个基向量组成的公共子空间Pg,Pg代表着每个性能级数据集Xi共同存在的变化,从Pg中判断筛选出真正的公共基向量=[pg,(1)pg,(2)···pg,(ˆA)],将原始数据映射到性能相关的过程变化的空间.采用DLV方法区分的动态关系和静态关系,依据自相关性提取出动态因素,即求出数据中前L带有最大自协方差绝对值的动态主要成分.

3.2 建立MSDLV离线模型

在化工过程中,动态过程数据中夹杂着大量噪声,过程变量和性能之间往往存在非线性关系和不确定性.考虑到实际工业过程中,很难准确地给每个样本点匹配具体的性能指标,从而进行精确的性能监测.故将运行稳定且性能相近的连续数据段划分成几个数据集,将性能指标模糊化.给每个性能级数据集中的所有样本对应同一个性能级标签,针对数据集之间是线性不可分的问题,采用MSDLV方法建立样本数据动态潜变量与性能级标签之间的非线性模型,如图2所示.

离线建模步骤如下:

1)采集性能级训练数据,进行标准化处理.

2)采用MSDLV算法去除性能级数据集共有的过程变化,将原始数据映射到式(10)的XSi空间,如图2中的所示.

3)采用DLV方法去除整体样本动态过程噪声和残差信息,根据自相关性提取动态主元变量作为下一步神经网络的输入,如图2中所示,分解公式如下:

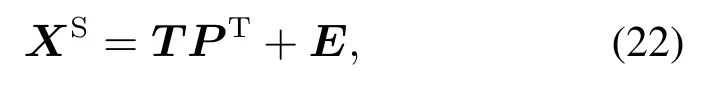
式中:XS是n个性能级数据中性能相关的过程变化组成的集合;P ∈RJ×L是加载矩阵;T ∈Rn×L是得分矩阵,代表XS的主要的动态过程变化;L是动态潜变量个数;E ∈Rn×J代表过程数据的静态变化,E空间的自协方差可忽略不计.

4)建立神经网络离线模型,如图2中所示.神经网络的输入为得分矩阵中的L个动态主元;输出包括C个二值化通道,如果训练数据属于性能级i,则第i个通道为1,其余为0.比如,过程的性能分成3级时,神经网络有3个输出通道,训练数据集合分别为

最优[X1∈RN1×J,y1=100];

一般[X2∈RN2×J,y2=010];

较差[X3∈RN3×J,y3=001].

网络隐含层的节点数可通过交叉验证法得到.

图2 性能级数据离线建模过程Fig.2 Offline modeling process of performance grade data

4 在线数据的状态分析与评估过程

4.1 在线数据的状态分析

实际动态过程的非故障数据表现为两种性能状态,稳定性能级状态和过渡性能级状态,可采用变遗忘因子的直线回归方法来分析在线数据所属状态[23–24].考虑到实际过程中测量数据对过程扰动的敏感性,在线评估时过程运行性能不能由单个样本衡量,因此需要将一个样本长度为H的数据窗口Xon,k=[xon,k(k −H+1)··· xon,k(k)]T作为基本分析单元[25],H的大小由生产过程的实际情况决定,但由于化工过程数据易受外部扰动和测量误差的影响,为了保证评估准确度,H不应过小.那么,定义在线样本的输出预测如下:

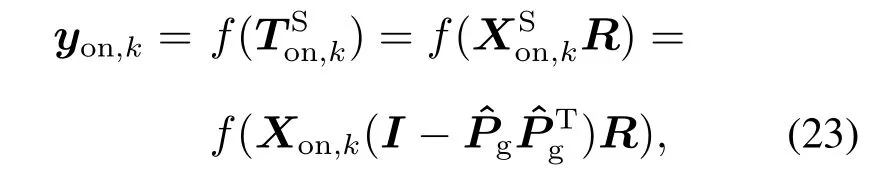
式中:f(·)为训练得到的神经网络非线性映射公式;yon,k=[y1,on,k ··· yC,on,k]∈RH×C为k时刻数据窗口中样本对应的神经网络输出,其中yi,on,k=[yi,on,k(k −H+1)··· yi,on,k(k)]T,i=1,2,···,C为第i个输出通道的输出序列.

计算第i个输出通道在遗忘因子β下的样本均值为

然后,对不同遗忘因子下的样本均值进行线性拟合,得到k时刻第i个输出通道回归直线的角系数:

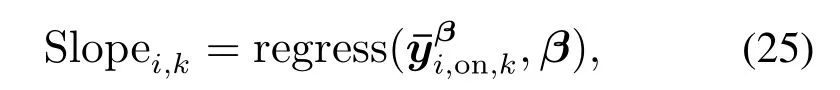
式中:直线回归的横坐标序列为遗忘因子β=[β1β2··· βn];直线回归的纵坐标序列为样本均值;由于相邻通道的回归直线趋势相反,则k时刻C个输出通道的平均角系数为

定义一个状态评估阈值ε,当|Slopek|>ε时,则k时刻数据窗口中样本的输出有向某方向明显变化趋势,此时动态性能为性能级之间的过渡状态;而当|Slopek|≤ε时,表明数据窗口中样本性能无向特定方向的变化,过程性能可能处于稳定性能级状态,也可能由于噪声和不确定因素的干扰样本性能波动较大.

4.2 在线评估过程

在线评估动态过程的具体步骤总结如下:

1)采集k时刻的在线过程数据,将训练数据的均值和方差进行标准化处理,得到长度为H的数据窗口Xon,k.

2)剔除在线数据中训练数据各性能级共有的性能不相关变化,公式如下:

3)运用DLV方法提取动态主元变量,得分向量由式(19)得到:

4)采用式(23)计算数据窗口中样本对应的神经网络输出yon,k ∈RH×C,并进一步计算,i=1,2,···,C和Slopek来衡量k时刻的性能等级和性能状态.

5)定义一个通道评估阈值α(0<α<1)用于判断过程的性能等级.α是基于历史数据和专家经验,通过交叉验证反复实验得到,能够最大限度减少在线错误评估的次数.评估策略如下:

Case 1如果表明k时刻在线数据与性能级i内的数据变量关系和幅值变化近似一致,过程运行在性能等级i.

Case 2如果Case 1 不满足,但|Slopek|>ε,则判断过程正处于性能级之间的过渡状态.

Case 3如果Case 1不满足,但|Slopek|≤ε,则在线数据受噪声和不确定性因素干扰较大,过程性能与前一时刻保持一致.

5 裂解炉实例应用

5.1 乙烯裂解工业过程描述

裂解炉是乙烯生产过程的核心生产装置,运行效率不仅影响下游生产设备的平稳操作,甚至还会影响整个乙烯生产装置的经济性能.本文采集的是国内某乙烯装置某台裂解炉的实际过程数据,该裂解炉主要用于裂解石脑油,裂解原料在对流段预热后,然后经过文丘里流量分配器进入辐射段炉管进行裂解反应.出辐射段炉管的高温裂解气进入极冷换热器,与锅炉给水换热后快速冷却并中止裂解反应.出急冷换热器的裂解气进入急冷器,由急冷油喷淋冷却至200℃左右,经过裂解气大阀,通过裂解气总管进入汽油分馏塔,过程模型简图如图3所示.乙烯裂解过程的单程高附加值产品收率和与过程热效率可以通过最大程度的控制可控变量的稳定性和设定值进行提升，进而提高裂解过程的经济性能[26–27].

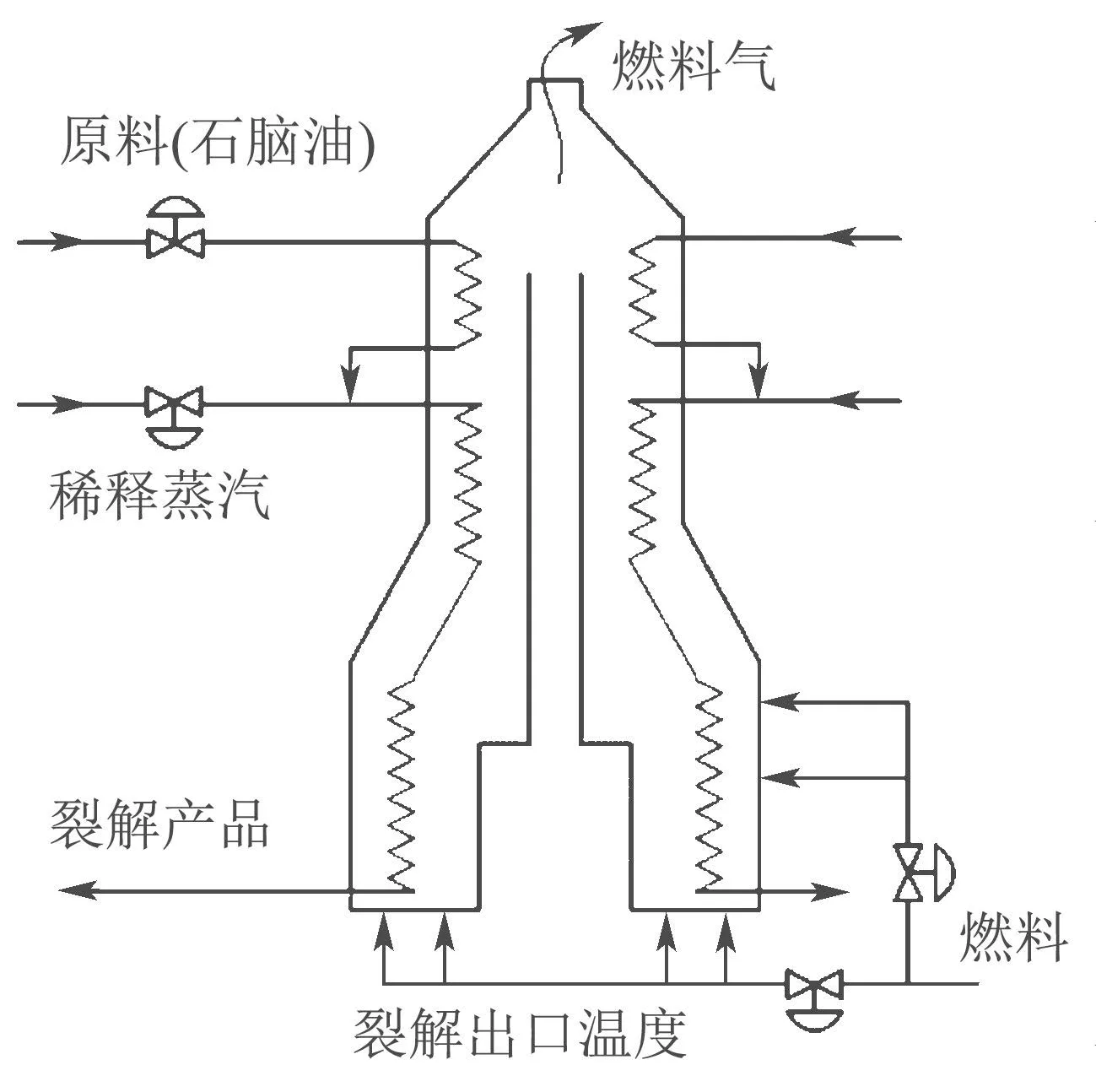
图3 乙烯裂解炉结构简图Fig.3 Structure of the ethylene cracking furnace

乙烯裂解过程的生产周期长,数据之间存在动态自相关性,因此如何根据实时数据在线评估过程的经济性能成为急需解决的问题.本文采用的MSDLV方法可以根据动态过程数据进行在线性能分级评估,能够及时检测到过程性能的变化.表1列出了实际过程中18个与性能相关的可测量的过程变量,用于划分训练数据集和测试数据集.过程的性能可以依据先验知识分成3个稳定性能级,训练数据集合和性能标签依次为

最优[X1∈R407×18,y1=100];

一般[X2∈R382×18,y2=010];

较差[X3∈R224×18,y3=001].

表1 用于经济性能评估的过程变量Table 1 Process variables for economic performance assessment

5.2 评估精确度分析

选取一段裂解过程运行性能稳定变化的样本数据用于验证基于MSDLV的在线经济性能分级评估方法的有效性.经过筛选后,数据集共包括1263个采样点进行测试,其性能的变化趋势为:最优→过渡→一般→过渡→较差.算法中相关参数设置如下:松弛因子δ=0.3;在线评估的数据窗口长度H=25;输出通道评估阈值α=0.85;状态评估阈值ε=0.2;遗忘因子β=0.5:0.1:1.4.

为了验证本文方法在评估准确度方面的优势,将采用基于MSPCA的建模方法对同一组测试数据进行评估对比.图4和图5分别是采用MSPCA和MSDLV方法得到的评估结果,图4(a)采用MSPCA方法将测试数据当作静态,映射到第一主元和第二主元方向.图5(a)采用MSDLV方法提取数据的动态潜变量,将数据映射到第一动态主元和第二动态主元方向.图4(b)–(d)和图5(b)–(d)是神经网络3个通道的输出,分别表示与3 个不同性能等级的相似度,虚线表示测试数据性能分级的区分标准值,从对比效果分析,可以看出MSDLV考虑数据自相关性得到的结果更加平稳、准确.MSPCA提取测试数据的主元,忽略了过程的动态相关性,得到的结果波动较大,出现了错误评估,较差数据段出现误判情况.

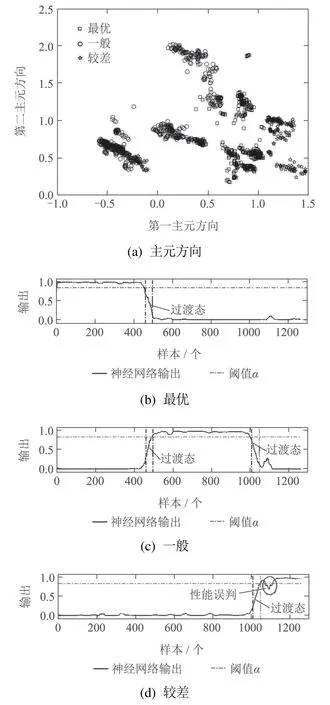
图4 基于MSPCA的在线评估结果Fig.4 MSPCA–NN–based online assessment results

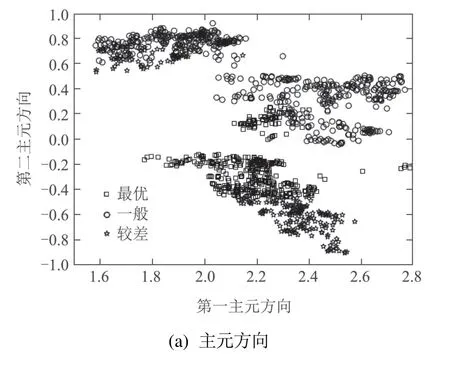
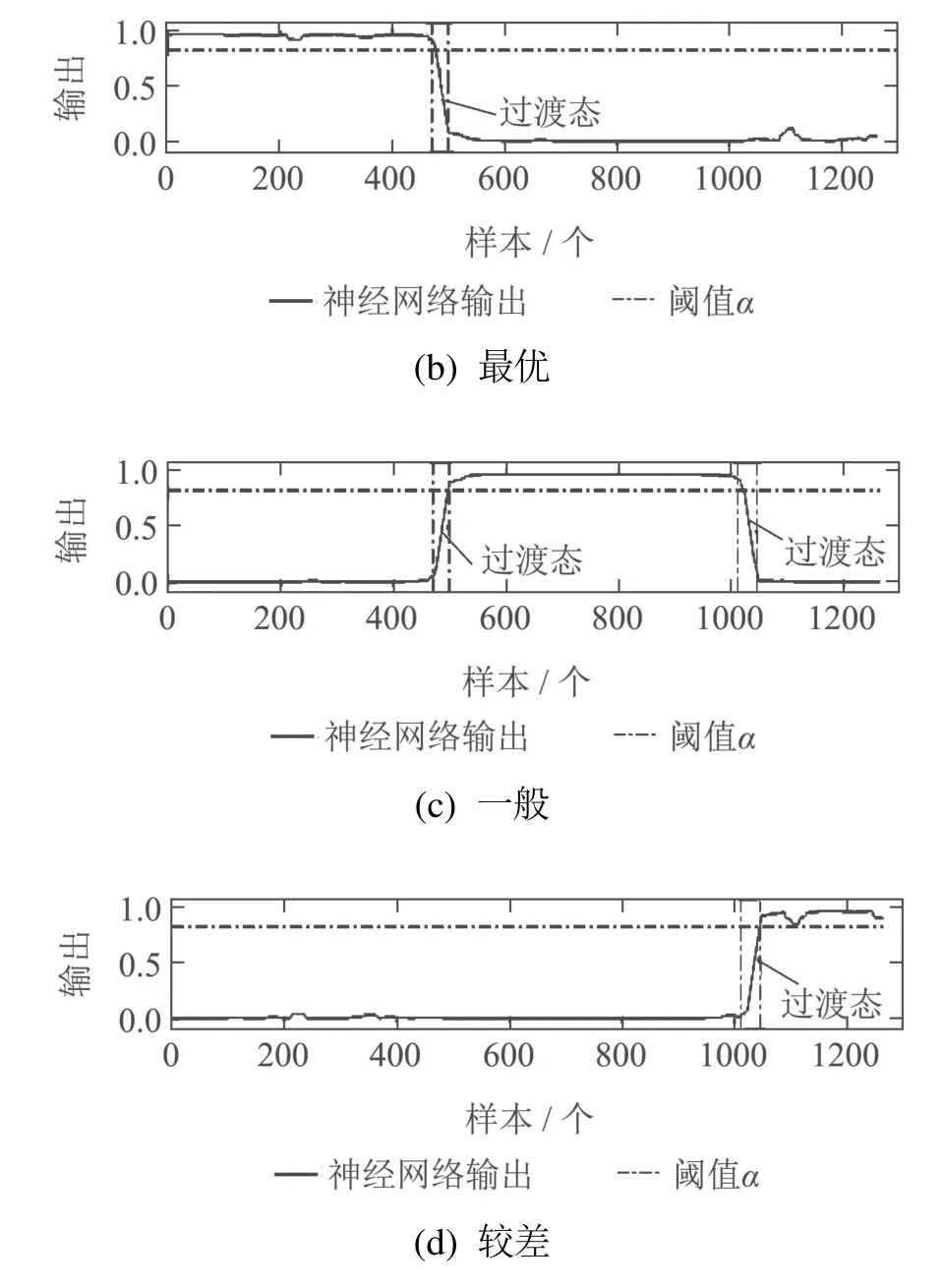
图5 基于MSDLV的在线评估结果Fig.5 MSDLV–NN–based online assessment results

图6和图7所示的是两种方法得到的在线评估过渡性能角系数,MSDLV方法得到的效果波动较小,判断数据的稳定态和过渡态的准确度较高.由于MSPCA在评估过程性能时出现误判,MSPCA方法得到的角系数波动较大.在较差数据段的角系数出现两次大的波动,稳定状态部分采样点超过状态评估阈值被误判断为过渡态.MSDLV由于考虑过程性能的稳定态与过渡态,在预估两种状态之间出现时滞,对总体数据性能评估的影响较小.

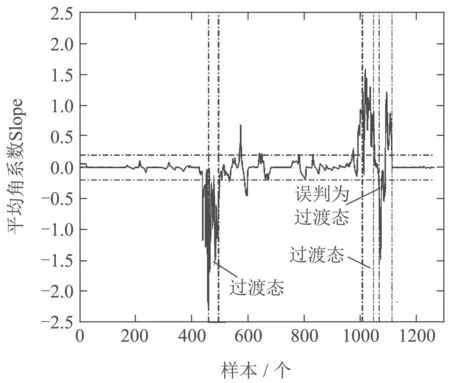
图6 基于MSPCA的在线评估过渡性能系数曲线Fig.6 Performance transition coefficient curve based on MSPCA online assessment method

图7 基于MSDLV的在线评估过渡性能系数曲线Fig.7 Performance transition coefficient curve based on MSDLV online assessment method

表2统计了MSPCA和MSDLV方法得到的在线评估结果与实际情况,通过对比评估正确的样本数量和样本总数的百分比可以得出MSDLV评估方法的准确度更高.基于MSPCA方法的精确度为92.5%,MSDLV评估采样点性能总体准确度达到了94.6%.MSDLV在区分动态过程的测试数据的过渡状态和稳定稳态的总体效果高于MSPCA,MSDLV评估动态自相关过程测试数据性能的全局准确度也更胜一筹.

表2 在线评估结果与实际状况的对比Table 2 Comparison of online assessment result and actual condition

6 结论

针对动态流程工业过程变量存在明显的自相关性,过程数据的动态特性难以提取,本文以连续多个性能相近的数据集作为研究对象,提出基于MSDLV的在线性能分级评估的方法.该方法通过提取稳态性能级之间性能相关变化的动态潜变量,提取的主元具有明显的动态特性.建立神经网络离线模型,有效拟合样本数据动态主元与性能标签之间的非线性关系,使动态过程性能评估具有强鲁棒性和高准确性.实际动态过程各安稳性能级状态之间存在着过渡状态,可以利用角系数准确地识别过渡状态.通过将MSDLV方法应用到乙烯裂解炉过程中,并与MSPCA方法进行对比,证明该方法是一实际可行,准确度较高的在线性能分级评估方法.本文采用自相关PCA方法提取延迟为1的时候的最大自协方差,可进一步研究模型参数选取策略确定延迟D+1,增强模型可解释性与精确度.