基于k近邻变量贡献与重构理论的工业过程故障诊断
2020-05-12王国柱胡永涛杜志勇
王国柱,胡永涛,李 元,杜志勇
(1.河南工学院电气工程与自动化学院,河南新乡 453003;2.沈阳化工大学信息工程学院,辽宁沈阳 110142)
1 引言
随着工业过程生产规模的不断扩大,系统复杂性的日益提高,有效的故障诊断方法成为了保证工业生产安全和提高产品质量的关键.基于统计理论的方法作为故障诊断领域的主要方法之一,已经受到了国内外研究人员的广泛关注并得到了较快的发展[1–10].该方法具有不需要建立系统精确数学模型的优势,主要依赖正常过程数据建立统计模型,从统计学角度对生产过程的安全性进行描述.另外,当检测到工业过程中存在故障时,提取有效的故障信息,研究各种故障和异常变量之间的关系,建立准确的“故障–征兆”表并将其作为后续故障决策与评价时可用的知识库是非常必要的,也成为目前故障诊断领域研究的热点问题[11–14].在基于统计理论研究的框架下,贡献图是最常用的异常变量识别方法,可以分为平方预报误差(squared prediction error,SPE)贡献图和T2贡献图两种[15],该类方法通过柱状图使每个变量的贡献值可视化,能够直观地显示出故障发生时各变量的贡献程度.故障发生后,贡献图方法通常认为对统计指标贡献较大的变量为可能造成过程故障发生的责任变量,但并没有确定贡献变量的控制阈值,即各个变量的贡献仅起到指导作用,最终的故障原因还需要过程经验丰富的操作人员进一步分析和确定;换句话说,即贡献图方法只能对变量贡献进行排序,大致找到发生异常的变量,并不能识别过程中所有发生异常的变量[16].类似主元分析(principal component analysis,PCA)贡献图方法,一些基于完全分解、局部分解和角度的异常变量识别方法也被相继提出,Alcala在文献[17]中也对这些方法进行了总结,并阐明了此类方法的优缺点.随后,基于重构贡献的方法也逐渐兴起,Qin等人[18]提出了一种基于传感器有效度指标的故障诊断技术,作者认为通过对异常传感器的数据重构,可以有效地减小SPE统计指标,在对没有发生故障的传感器变量重构时,由于故障信息仍然存在,重构后的SPE值与故障时没有太大的变化,这也为异常变量的辨识提供了保障;Alcala和Qin[19]提出了一种基于重构贡献(reconstruction based contribution,RBC)的故障诊断技术,验证当只发生传感器故障时,重构贡献图方法的诊断准确率要高于传统贡献图方法.虽然上述方法在对过程中异常变量进行识别时具有较高的准确性,但它们通常需要假设故障方向已知或过程中已经具备经验知识,而过程中准确的假设和有效经验的获取具有一定的难度,并且该类方法和传统贡献图方法一样不能避免变量之间的扩散效应[20].
近年来,基于k–NN理论的故障检测方法已经被提出并成功用于监视连续过程和间歇过程.但由于该方法的计算量大,需要存储的中间值多,k–NN方法对计算机的计算速度与存储空间就有较高的要求.为了解决这些问题,He等人[21]提出了PC–k–NN方法,该方法采用原始样本的主成分作为建模样本,既降低了计算距离的运算量,又节省了存储空间,但该方法忽略了发生在残差空间的异常信息.随后,Li等人[22]提出了一种基于特征空间k最近邻(feature spaceknearest neighbor,FS–k–NN)的批次过程故障检测方法,该方法结合特征空间的主元部分和残差部分全面表示原始数据的有用信息,取得了一定的效果.尽管k–NN方法在故障检测领域已经取得了令人满意的成果,但在故障诊断与异常变量识别方面的研究较少.因此,在没有可用故障数据知识和经验的情况下应用k–NN方法进行异常变量的有效识别存在一定的挑战,也具有一定的学术研究价值和实际意义.
基于以上讨论,本文提出了一种基于k近邻变量贡献与重构理论的工业故障诊断方法,该方法不需要进行数据变换,并且能够有效避免因变量扩散效应带来的影响.首先,从过程正常运行数据集中提取每个样本在k–NN检测阶段的距离统计指标,将其细化并分解为各变量的贡献值,并分别从单变量异常和多变量异常角度研究方法的可行性,保证异常变量具有较大的贡献,进而利用核密度估计方法确定各个变量贡献的控制阈值;其次,当样本存在故障时,将异常样本的k近邻距离统计指标分解到每个变量,确定当前样本中各个变量的贡献,并与正常模型中的控制阈值比较,“一次”识别该样本中存在的异常变量;再次,研究了基于k–NN理论的数据重构方法,对“一次”识别到的异常变量进行重构;当重构后样本经过k–NN检测仍然存在故障时需返回贡献分析阶段进行异常变量的“二次”识别,直到找到过程中发生异常的所有变量,最终建立准确的“故障–征兆”表.本文采用数值仿真与CSTR系统验证了所提出方法的有效性和可靠性.
2 基本理论
2.1 k–NN基本规则
k–NN近邻法,又称k–NN分类法,它是一种可以预测未知类或标签的非参数监督分类方法,对于未知分布和非正态分布的数据集可以获得较高的分类准确率,具有健壮性强,概念清晰和适用非高斯、非线性数据等诸多优点[22].假若一个样本在特征空间中的k个最相似(距离最近)样本大多数都属于某一个类别,则此样本也属于这个类别;只有当新的样本与其在训练样本的前k个最近邻的距离超出类别属性时,称该样本与训练样本具有较大差异[23].目前,该思想已经被应用于工业过程故障监视.
2.2 基于k–NN规则的故障检测
基于k–NN的过程故障检测方法直接利用正常工作条件下的过程数据,选取每个样本的前k个邻近数据样本建立过程的统计模型,提取正常样本之间的最近邻距离特征量,确定模型的统计控制限,进而对实时样本进行检测.假设采集到的过程正常运行数据集为Xn×m,n为样本个数,m为变量或传感器个数,k–NN方法可以通过图1步骤进行故障检测:
1)标准化正常过程数据Xn×m,将其转化为零均值,单位标准差的矩阵xn×m;
2)根据式(1)计算正常数据集中任意样本xi与其他样本之间的欧氏距离d(xi,·)并对其排序,找到xi的前k个最近邻样本N1(xi),N2(xi),···,Nk(xi);
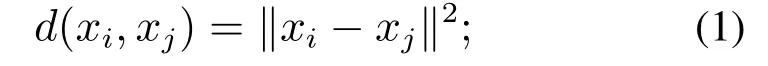
3)根据式(2)计算每个正常样本xi与其k个近邻的距离统计量:

4)使用核密度方法[24]对3)中所得到的n个距离统计量进行估计,确定置信度为99%的控制限δLimit;
5)对于新采集到的实时数据xnew,采用建模时的均值及标准差进行标准化处理;
6)求取其与训练样本的前k个最近邻的距离并计算统计指标(k个最近邻距离平方和);
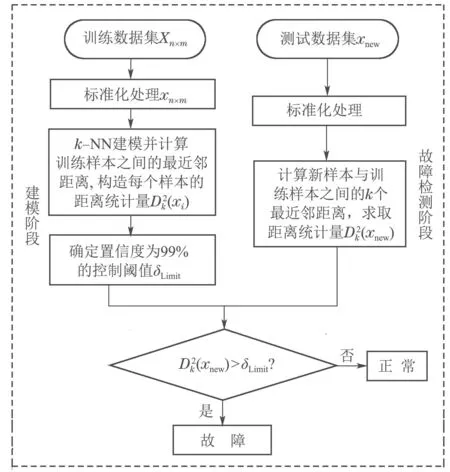
图1 k–NN建模与故障检测过程流程图Fig.1 Flow chart of k–NN modeling and fault detection
3 k–NN变量贡献方法
从上述k–NN建模过程中可以得到,式(2)为样本xi的距离统计量,由m个变量的贡献累加和构成,因此,可以将分解为m个变量的累加和,如式(3)所示:
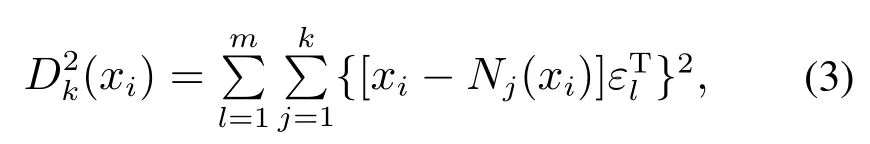
其中εl为第l个元素为1、其余元素为零的行向量.
此时,式(4)可以定义为样本xi中第l个变量对距离统计指标的贡献:
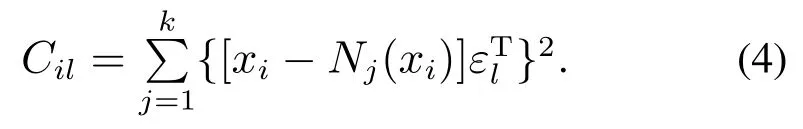
根据式(3)和式(4)可知,样本的k–NN统计量与各变量的贡献之间存在如下关系:
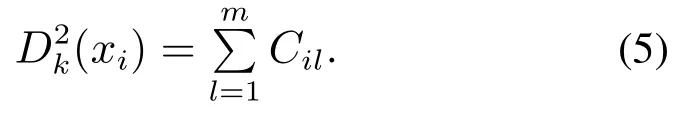
根据以上分析得到,样本xi的第l个变量对距离统计指标的贡献实际上等于该样本与其k个最近邻第l个分量的平方距离之和,即变量贡献分析时仅考虑了变量自身的影响,并没有考虑各个变量之间的关系,可以有效避免变量之间的扩散效应,但在过程故障时是否能够保证异常变量对统计指标的贡献一定大于其他变量需做出进一步说明.下面分两种情况对k–NN变量贡献方法的可行性进行了分析,分别为单变量异常情况和多变量异常情况[25–26].
3.1 单变量异常情况的可行性分析
假设样本xf为故障样本,该样本中只有第r个变量偏离正常运行范围,此时故障样本xf可以分解为

式(6)中:x∗为该样本的正常部分;εrfr为异常部分,εr为故障方向,表示该样本中第r个变量发生异常,fr为对应方向上的故障幅值.将式(6)代入式(4)得到

在式(7)中,由于Nj(xf)表示xf在正常数据集中的近邻样本,而x∗为xf中包含的正常部分,因此存在x∗−Nj(xf)≈0,此时,式(7)可以近似表示为
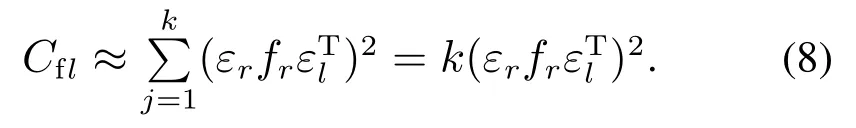
式(8)表示样本xf中第l个变量的贡献,且存在关系
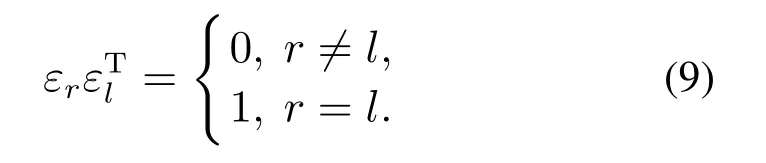
当故障方向r=l时,异常变量的贡献值Cfr=;而其余变量的贡献值Cfl ≈0,即存在关系

根据上述讨论可知,k–NN变量贡献方法可以保证单个变量异常时其贡献最大.
3.2 多个变量异常情况的可行性分析
样本xf为故障样本,该样本中存在多个变量偏离正常运行范围,此时假设异常变量个数为3个,分别为变量a,b,c,此时故障样本xf可以分解为如下形式:

同上,式(11)中:x∗为该样本的正常部分,εafa,εbfb和εcfc为异常部分,ε和f分别为相应的故障方向和故障幅值.将式(11)代入式(4)得到
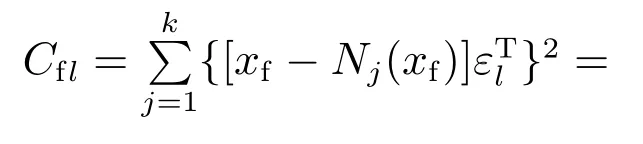
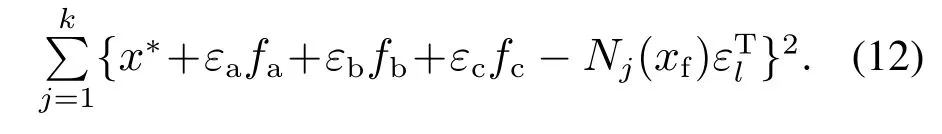
同理,式(12)中存在x∗−Nj(xf)≈0,此时,式(12)可以近似表示为
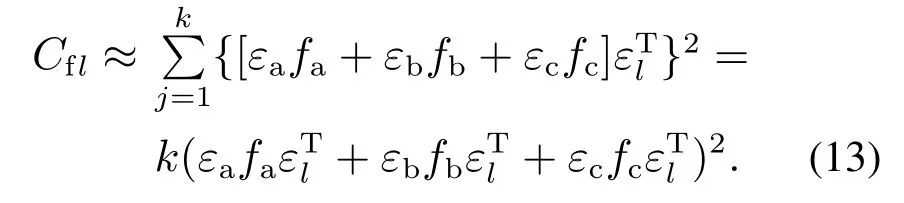
与单变量异常情况类似,当故障方向为a,b,c时,可得

根据上述讨论可知,k–NN变量贡献方法对多个变量发生异常情况同样有效,可以保证变量异常时其贡献大于其他变量的贡献值.
3.3 k–NN变量贡献控制阈值的确定
变量贡献控制阈值描述的是变量在正常工况下的波动情况,也就是说,故障样本的异常变量贡献会大于正常样本中该变量对距离指标的贡献.由于在建模过程中使用的数据均来自正常过程且处于稳定状态,因此建模时每个变量对统计指标的贡献应该相对稳定,此时可以使用正常样本中各变量贡献组成的矩阵C进一步确定每个变量贡献的控制限.文献[23,26]介绍了使用非中心χ2分布计算k–NN距离控制限的方法,作者认为每个样本的k近邻距离统计指标近似服从非中心χ2分布,可以通过χ2分布函数确定某个自信水平的控制阈值,但文中并没有论证距离统计指标是否服从非中心χ2分布.本文采用不需要贡献指标服从分布假设的核密度估计方法[24]计算正常过程变量贡献的控制阈值,结果为
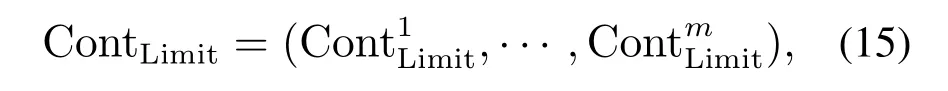
其中:ContLimit为正常运行过程中所有变量贡献的控制阈值集合;元素表示在过程正常运行时第i个变量贡献控制阈值.
4 基于近邻重构的故障诊断方法
4.1 异常变量的“一次”识别
对于过程中采集到的实时样本,使用k–NN方法进行故障检测,当统计指标大于控制阈值时,表示系统中存在故障.随后,为了确保设备能够恢复到正常状态,需要对该故障样本进行异常变量识别,判断哪些变量没有跟随正常过程的运行轨迹.下面对k–NN故障检测及基于变量贡献分析的异常变量“一次”识别过程进行了介绍:
1)对于新采集到的实时数据X1×m,采用建模时的均值及标准差处理,得到xtext;
2)求取xtext与训练样本的前k个最近邻的距离并计算统计指标D2(xtext);
3)将D2(xtext)与正常过程统计量的控制限δLimit比较,如果统计量小于控制限,即D2(xtext)≤δLimit时,表示该样本正常;反之,样本发生故障,此时,测试样本xtext可以描述为故障样本xf;
4)对于故障样本xf,根据式(16)计算每个变量对该样本的k–NN 贡献统计指标,其中,Nj(xf)表示xf在建模数据中的第j个近邻;
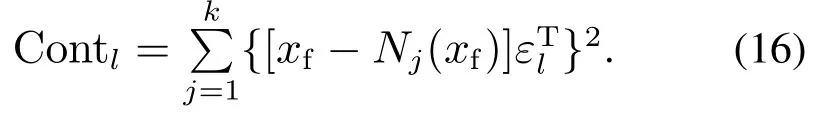
5)将故障样本中每个变量的贡献值Conti与式(15)中正常过程变量贡献的控制阈值比较,如果贡献值小于控制阈值,表示样本中该变量正常;反之,该变量发生异常.
4.2 异常变量的“二次”识别
本节提出了一种基于k–NN理论的数据重构方法,目的是使用该重构方法对故障情况下根据变量贡献值和变量贡献阈值“一次”识别到的异常变量进行数据重构,进而对重构后的样本再次进行故障检测,当重构后样本中无故障时,异常变量识别过程结束;反之,需返回变量贡献分析阶段进行“二次”识别.
重构方法:为方便理解,变量重构时假设过程中仅有一个变量发生异常,结合图2对计算过程中几个符号和参数进行了定义.
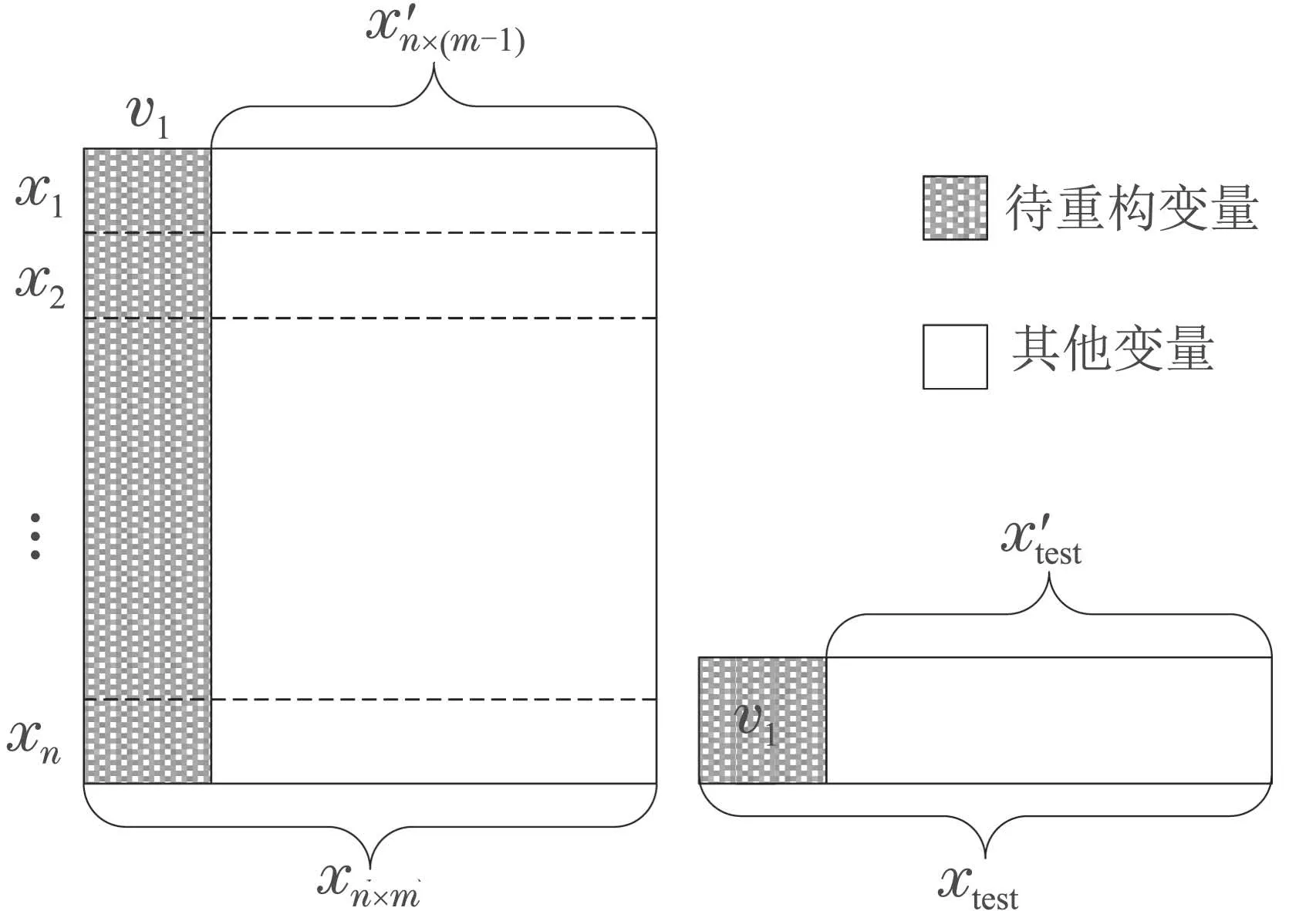
图2 变量重构细节图Fig.2 The detail of variable reconstruction
具体定义内容如下:1)xf为故障样本,为样本xf去掉异常变量后由剩余变量组成的样本,参见图2,阴影部分的v1为贡献分析和“一次”识别方法确定的异常变量;
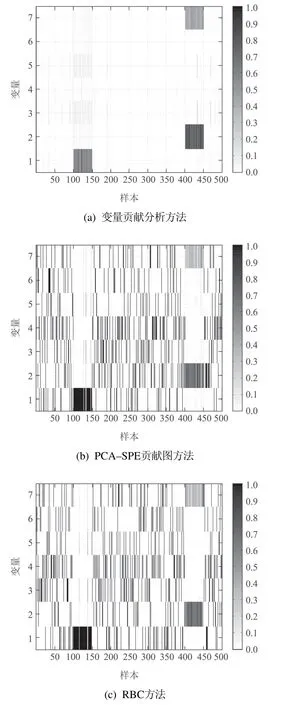
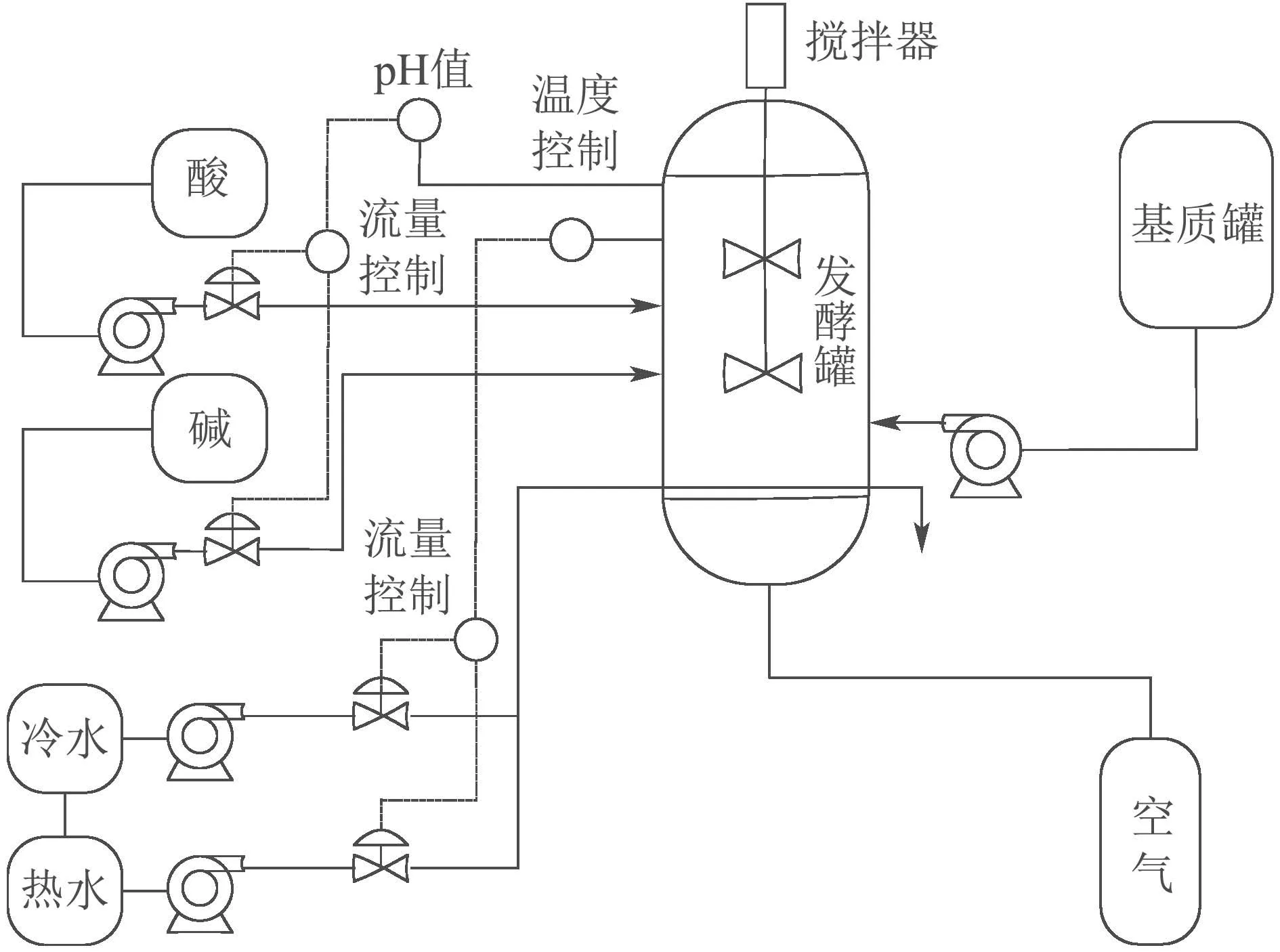
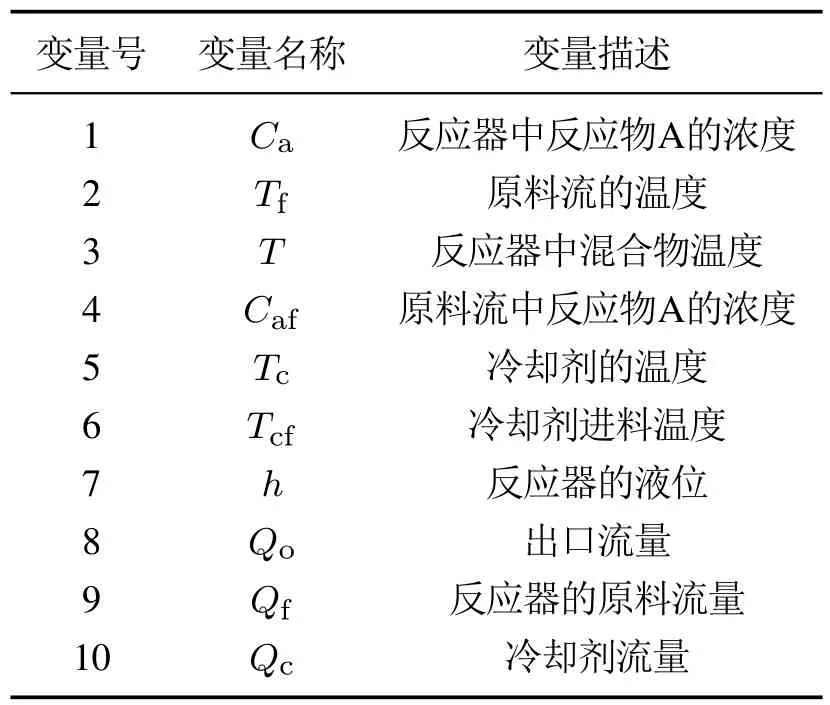
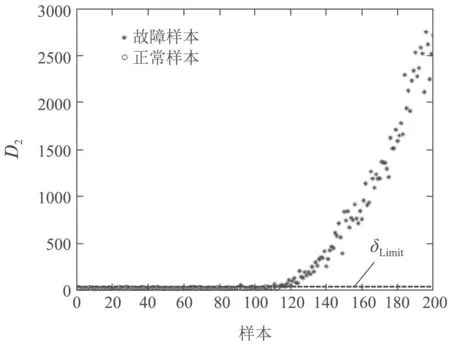
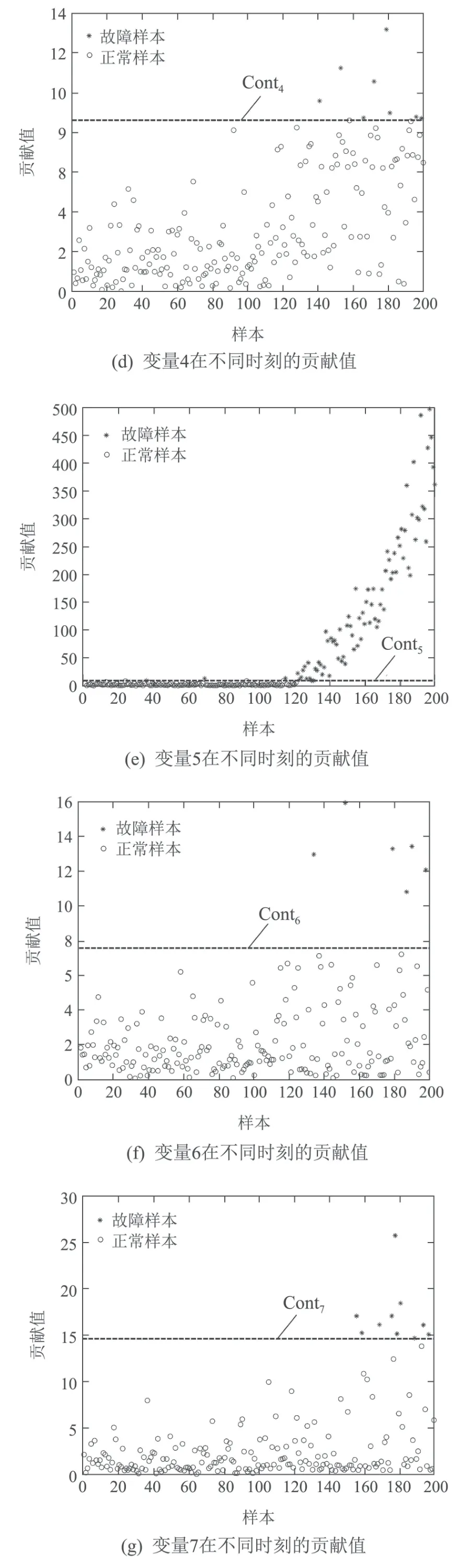
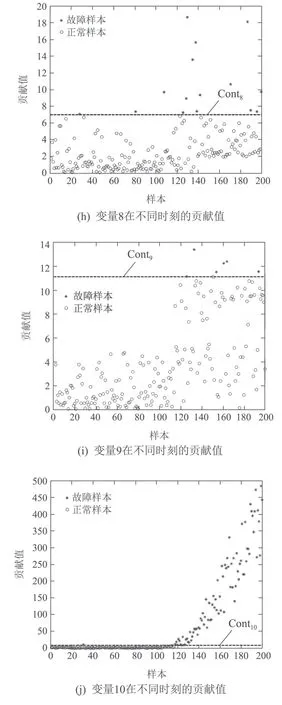
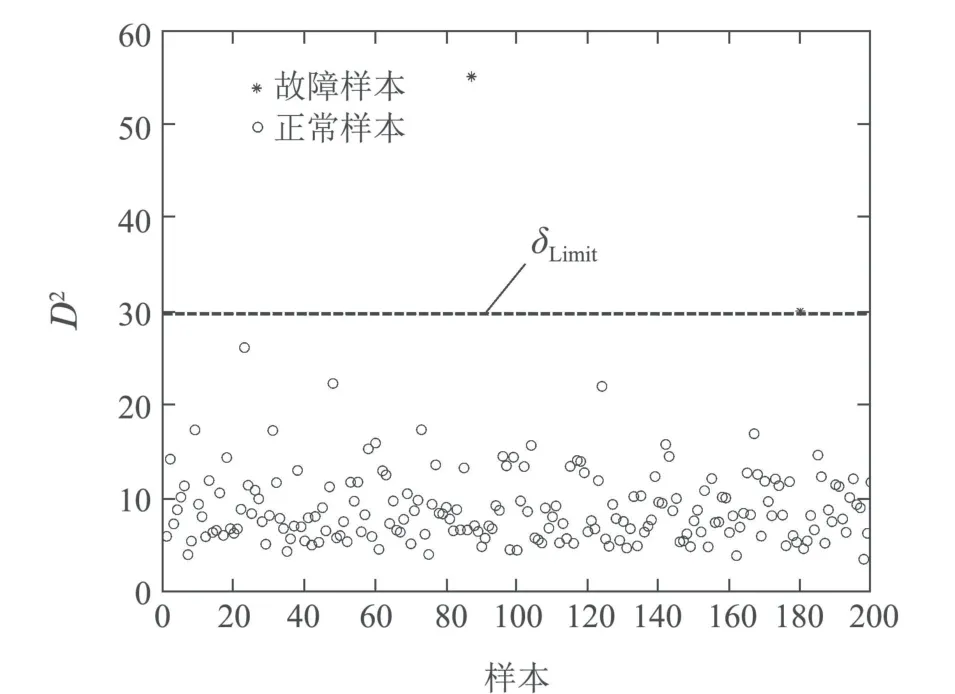
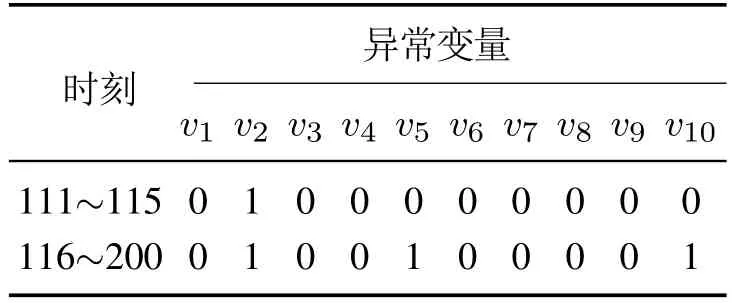
3)d1,d2,···,dk分别为与其在中前k个最近邻样本之间的欧氏距离,样本标签为,j=1,2,···,k且满足d1 进行数据重构时,首先要根据式(17)确定能够使重构误差达到最小的k值,当k值确定后根据式(18)重构变量v1. 根据前文介绍的k–NN建模、变量贡献分析、故障检测以及异常变量“一次”识别方法,本节绘制了基于贡献分析与数据重构的异常变量精确识别过程流程图,如图3所示,并根据该图介绍了异常变量的“二次”识别方法(假设该过程仅有两个变量发生异常:变量v1和v2). 1)采用上述重构方法对故障样本中的异常变量v1和v2进行重构,重构后可表示为变量v1c和v2c,此时原故障样本可以被重新描述为xfc,如图3所示; 2)对于xfc,寻找其在建模阶段训练数据中的前k个最近邻,并根据式(2)计算该样本点与其近邻的平方距离D2(xfc); 3)比较距离指标D2(xfc)和控制阈值δLimit,判断此时该样本的统计指标是否恢复到正常统计范围之内.当距离指标已经处于正常状态时,识别过程结束,异常变量仅为变量v1和v2;否则,将重构变量v1和v2后的新样本转入变量贡献分析并进行故障样本的“二次”异常变量识别,直至在对重构后的样本故障检测时检测不到故障存在为止. 图3 基于k–NN变量贡献分析与数据重构的异常变量精确识别过程流程图Fig.3 Flow chart of abnormal variable identification based on k–NN variable contribution analysis and data reconstruction 本节给出了数值仿真和连续搅拌釜式反应器(continuous stirred tank reactor,CSTR)系统验证提出方法的有效性.首先通过一个七变量数值仿真实例,对比基于PCA的贡献图和RBC方法的异常变量识别结果,验证了提出方法的有效性;然后针对CSTR系统中的实际故障进行方法的应用研究. 数值仿真由两个潜隐变量s1和s2构造的七变量数据组成,如式(19)所示: 式中:e1~e7是均值为零、标准差为0.01的噪声,s1是从−10 到−7 之间的随机数,s2服从正态分布N(−15,1).根据式(19)共产生500个训练样本用于建立故障检测模型;500个待测试样本用于验证基于变量贡献分析和数据重构方法在异常变量识别方面的有效性,其中,故障添加方式如下: 1)x1从101~150时刻添加8%的阶跃故障; 2)x2从401~450时刻添加10%的阶跃故障; 3)x7从401~450时刻添加5%的阶跃故障. 图4给出了测试数据的k–NN故障检测结果,从图中可以明显看出系统分别在101~150和401~450时间段内控制指标超出了控制阈值范围,即此时段系统中存在故障,且与预设故障时间一致.文中所有图中“∗”表示发生故障样本,“◦”表示正常样本. 图4 测试数据的故障检测结果Fig.4 Fault detection results of test data 在检测到过程中存在故障后,需要进一步识别过程中的异常变量.首先,根据正常数据中每个变量对控制指标的贡献值计算其控制阈值;其次,计算测试数据中每个时刻的变量贡献值,并与正常过程中各变量的控制阈值比较,结果如图5所示. 从图5(a)中可以看出,x1的贡献指标在101~150时刻超出控制阈值,即在这段时间内x1异常;x2和x7均在401~450时间段超限(图5(b)和(g)),即该段时间内异常变量为x2和x7;而其余变量的贡献指标均在控制范围之内,无异常,如图5(c)–(f)所示.此时,异常变量的“一次”识别过程结束. 图5 变量贡献分析结果Fig.5 Variable contribution analysis results 随后,需要对得到的异常变量进行重构并检测重构后样本是否回复正常状态,图6给出了使用重构方法将101~150时间段变量x1,401~450时间段变量x2和x7重构之后的k–NN故障检测结果,可以看到此时所有时刻的距离指标均处于控制阈值之内,过程中已经没有故障,异常变量的“二次”识别过程结束. 为了能够将本文所提方法与传统方法进行比较:图7分别给出了3种不同方法的异常变量识别结果,图7(a)为本文方法的异常变量识别结果,图7(b)和图7(c)分别为基于PCA–SPE的贡献图和基于重构贡献(RBC)方法的识别结果,图中颜色越深,表示变量贡献值越大.可以看到后两种方法虽然在故障发生时间段均能够显示异常变量贡献值较大,但并不能避免因PCA数据变换而造成的扩散效应;相比之下,图7(a)效果更优,变量之间的扩散效应明显消除,验证了所提方法的有效性.表1记录了该例的“故障–征兆”关系,精确地显示了不同时间段内过程中发生异常的变量. 图6 测试数据重构变量x1,x2和x7后的故障检测结果Fig.6 Fault detection results of test data after reconstructing x1,x2 and x7 图7 变量贡献图Fig.7 Variable contribution plots 表1 异常变量识别结果Table 1 Results of abnormal variables recognition 在本节中,通过CSTR系统[27]对提出的异常变量精确识别方法的有效性进行了验证,CSTR过程的详细描述如下:CSTR是聚合化学反应中广泛使用的一种反应器,其中反应原料以稳定的流速进入反应器,反应物以同样地稳定速率流出.由于强烈搅拌的作用,使刚刚进入反应器的新鲜物料与存留在反应器中的物料瞬间达到完全混合,反应器内部的物料浓度和温度处处相等,连续搅拌釜式反应器中的反应速率即由釜内物料的温度和浓度决定,系统的原理如图8所示.反应器的液位和温度采用串级控制.基于质量、能量和物料平衡的系统动态方程如式(20)–(23)所示: 其中:A是反应器的横截面积;Ca是反应器中反应物的浓度;Caf是原料流中反应物的浓度;Cp是反应物的热容量;Cpc是冷却剂的热容量;E是活化能;h是反应器的液位;k0是指数因子;Qf是进入反应器的原料流量;Qo是出口流量;Qc是冷却剂流量;R是通用的气体常数;T是反应器中混合物温度;Tc是冷却夹套中冷却剂的温度;Tcf是冷却剂进料温度;Tf是原料流的温度;U是热转移系数;Ac是总的传热面积;∆H是反应热;ρ是反应器中混合物的密度;ρc是冷却剂的密度. 图8 连续搅拌釜反应器系统原理图Fig.8 Diagram of the CSTR process CSTR系统的化学反应通常受到物料浓度和温度的限制,实际生产过程中催化剂活性的降低、进料温度的变化、进料浓度的变化、热交换器的结垢、传感器故障等都可能影响到产品的质量.因此,为了模拟并检测工业过程中的实际故障,采集正常条件下和故障条件下的数据,表2也分别设置了6种不同的过程故障,包括阶跃和斜坡两种类型.本文选择过程中的10个变量用于仿真和算法验证,变量描述见表3.正常过程和故障过程采样数均为200,且故障情况从101时刻开始引入,持续到过程结束. 表2 CSTR系统的故障描述Table 2 Fault descriptions of CSTR system 表3 CSTR过程监控变量Table 3 Process monitoring variables of CSTR 首先,使用k–NN故障检测方法对CSTR系统中的故障2数据进行检测,从图9给出的结果可以看出,故障引入时间为110时刻,与故障添加时间存在大概10个采样时间的滞后,这是由于该系统中故障2为斜坡型故障,故障刚引入时系统中变量仅发生了微小的变化,此时统计指标的改变程度很小,难于检测到故障的存在. 图9 故障2的检测结果Fig.9 Detection results of fault 2 其次,根据正常样本集的变量贡献分析方法确定正常过程中每个变量的贡献阈值,并与故障时间各变量的贡献指标比较,得到如图10所示的变量贡献分析结果.从图10中可以看到,变量2(原料流的温度Tf)、变量5(冷却剂的温度Tc)和变量10(冷却剂流率Qc)的贡献跟随故障情况发生变化,即故障2发生后产生的征兆为变量为2,5和10异常. 图10 变量贡献分析结果Fig.10 Variable contribution analysis results 再次,图11(a)给出了161时刻各变量贡献值与贡献控制限,“·”表示各个变量的贡献控制阈值,可以看出此时过程中仅有变量2,5和10超限;图11(b)给出了所有时间段内各个变量的全局贡献图,可以看到在故障引入初期,仅变量2贡献突出,随后变量5和10逐渐发生变化;最后,为了验证异常变量识别结果的准确性,使用数据重构方法依次将变量2,5和10在101~200时间段的数据重构,并重新进行k–NN故障检测,从检测结果可以看到此时距离统计指标均处于控制阈值之内,如图12所示,异常变量识别过程结束. 图11 变量贡献图Fig.11 Contribution plots 图12 故障2重构变量2,5和10后的检测结果Fig12 Detection results of Fault 2 after reconstructing variables 2,5 and 10 表4记录了CSTR系统中故障2的异常变量精确识别结果,即“故障–征兆”表,其中“0”表示变量正常,“1”为异常变量. 表4 故障2的异常变量识别结果Table 4 Results of abnormal variables recognition of fault 2 通过对CSTR系统工艺流程分析可以得到,在故障2引入初期(110~115时刻),过程中仅有变量2发生异常,与表2中描述相符,后期由于进料温度的斜坡上升导致反应器温度升高,为了控制反应器内温度达到目标值,需要调整变量5冷却剂温度Tc和变量10冷却剂流率Qc,因此,在后期时段中的异常征兆变量为2,5和10.该系统实例验证了本文所提出的基于k近邻变量贡献与重构理论可以精确辨识过程中每种故障与其对应时刻和变量之间的关系,即“故障–征兆”表,并且与故障设置情况相符. 本文主要在k–NN故障检测方法的基础上,通过将各个采样时刻样本的距离控制指标细化,分解为每个变量的贡献并对贡献做出详细分析,提出了一种基于变量贡献分析的异常变量识别方法;为了能够验证异常变量是否对控制指标具有较大的贡献,分别针对单变量异常和多变量异常情况进行了可行性分析,并在此基础上研究了异常变量的“一次”识别方法;随后,研究了基于k–NN理论的数据重构方法,详细地分析了算法原理;当重构后样本经过检测仍然存在故障时需返回贡献分析阶段进行异常变量的“二次”识别,直到找到过程中发生异常的所有变量,并建立准确的“故障–征兆”表.最后通过数值例子和在CSTR系统中的仿真验证了提出方法的有效性和可行性.下一步计划在本文识别出故障发生时的异常变量的基础上,深入研究各种故障与异常变量之间的确定关系,并从故障情况下异常变量之间的传播关系,并发关系以及耦合关系入手,准确分析导致故障发生的原因,为操作员合理分析故障,排除故障提供有效依据.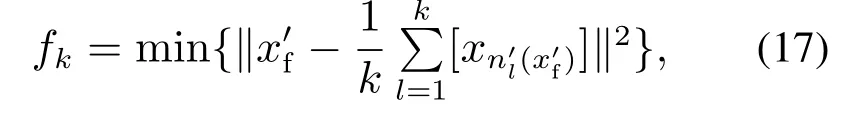
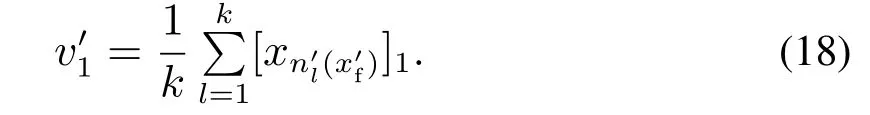
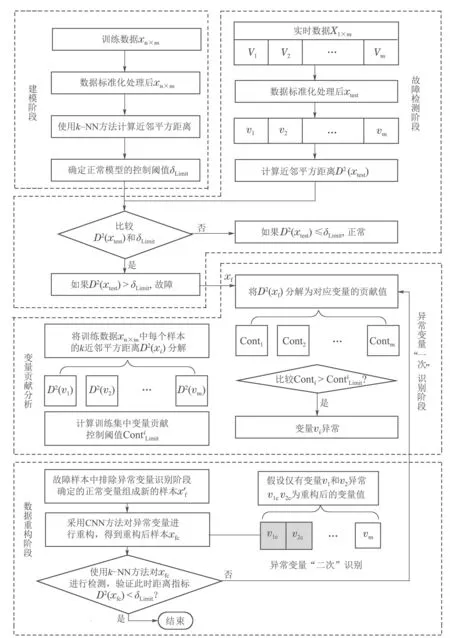
5 仿真研究
5.1 数值仿真
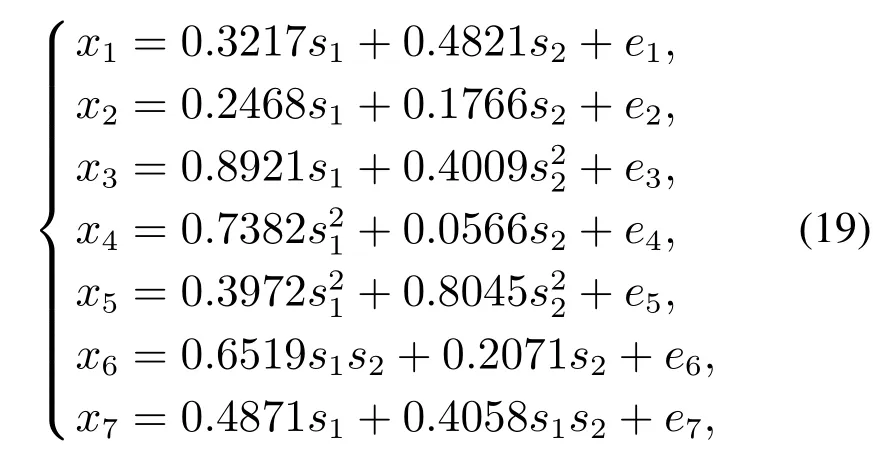
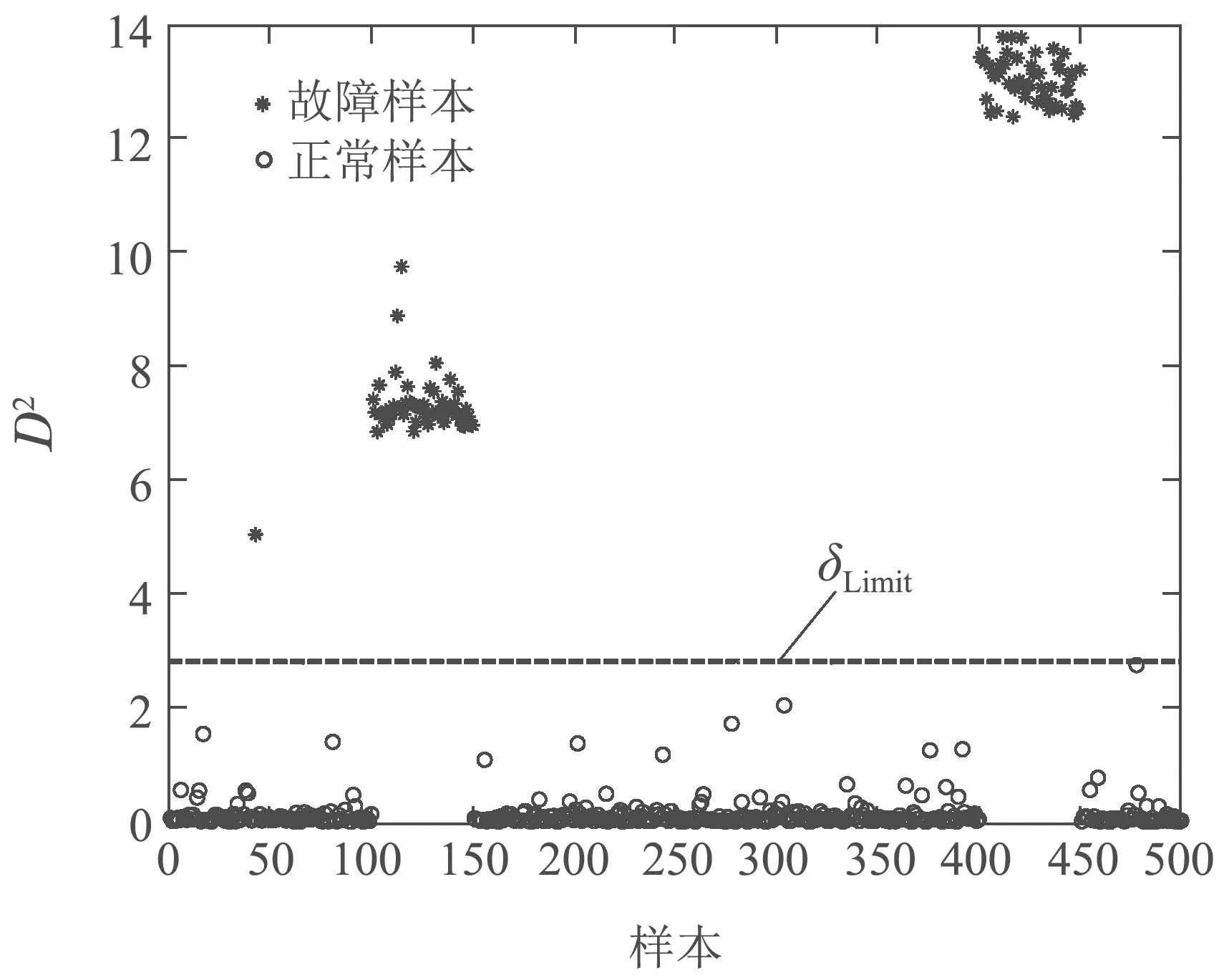

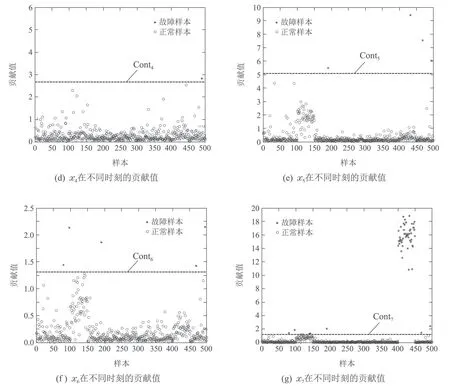
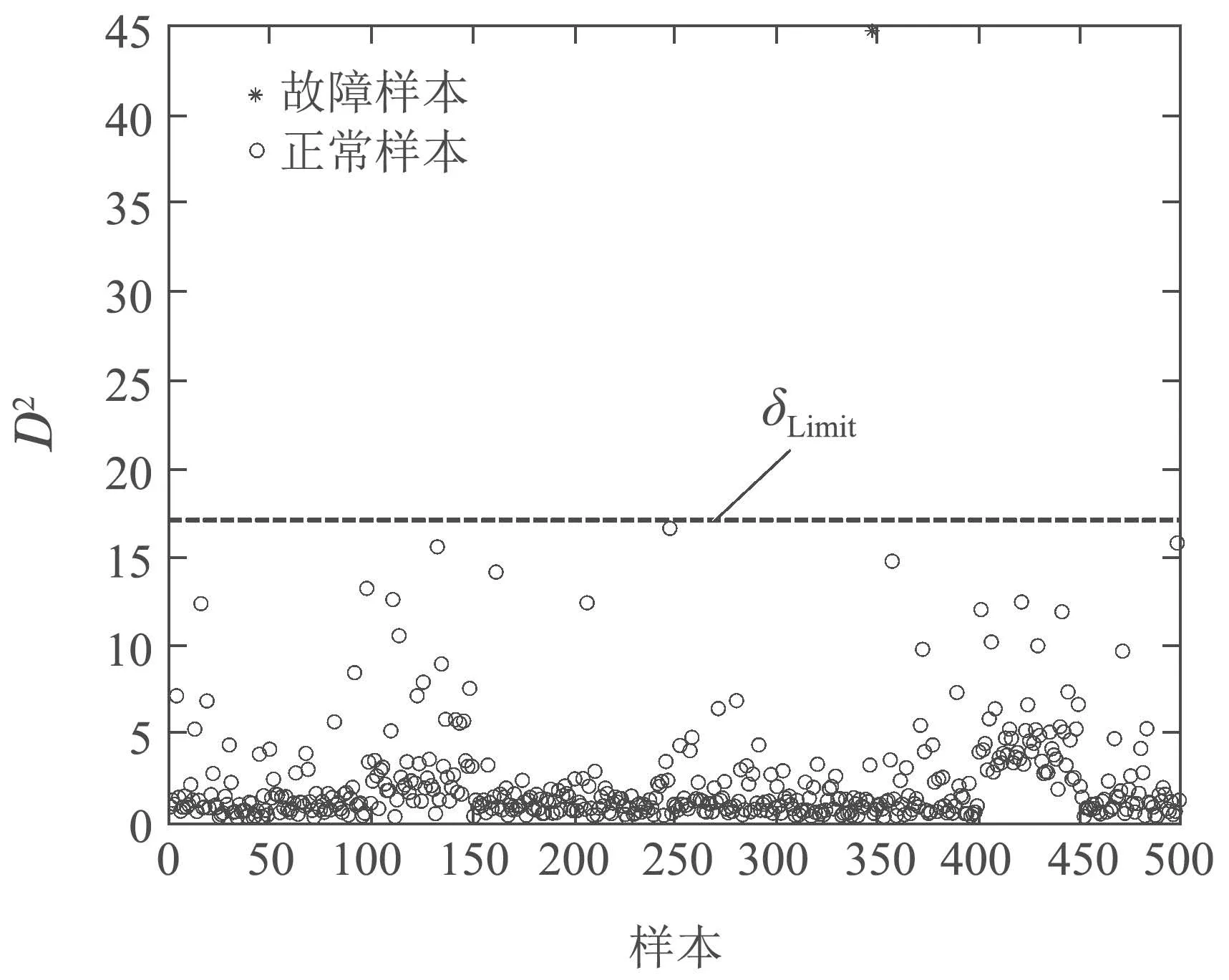

5.2 CSTR系统中的应用研究




6 结论和进一步的工作
