带结构风险最小化的最优区间回归模型辨识

刘小雍,方华京,陈孝玉

(1.遵义师范学院工学院,贵州遵义 563006;2.华中科技大学自动化学院,湖北武汉 430074)

1 引言

工业过程中的大多数控制系统结构主要是基于传统控制理论方法进行设计的,其适用范围受到了一定的限制,包括假定该过程为线性变化且整个过程的数学模型为准确已知[1].然而,大多数物理系统包含复杂的非线性及耦合关系等因素,导致很难建立准确的数学模型;此外,对来自控制系统中的过程参数变化、外部干扰或传感器失效也对控制系统的设计增加了诸多不确定性[2].这些现象的存在更需要探索一种更有效的建模方法,能够实现复杂的输入–输出映射及非线性函数逼近.因此,出现了基于数据或数据驱动的建模方法[3–4],即通过传感器或其他数据获取设备获取被控系统的输入–输出数据,采用神经网络[5]、Takagi-Sugeno(T–S)模糊模型[6]、支持向量机[7]等方法建立复杂系统的数学模型,这些方法的共同特点是建立的数学模型一般是确定的,不受系统参数变化、测量噪声或其他不确定性等因素的影响,具有一定的局限性:1)确定的数学模型不能自适应系统的变化;2)基于训练数据建立的数学模型结构较复杂、泛化性能差等.

然而,在众多的实际应用中,获取的信息往往呈现出不确定、不准确以及不完整等特征[8],对于这一类特征的信息描述,若仍采用传统的确定性数学模型建模,显然不能更好的去捕捉这一类不确定性复杂系统的特征变化[4].因此,针对不确定性复杂系统建模的研究,开始了从确定性数学模型到不确定性数学模型的扩展,包括模糊理论结合其他参数求解方法[9–10]、概率统计中的分位方法[11]、神经网络的上下界建模方法[12–13]等.文献[10]最早将possibility 与necessity回归模型相结合,采用模糊输出对区间回归进行分析,并应用二次规划对possibility与necessity回归模型进行参数求解.基于文献[10]的探索,又出现了模糊数据的另一种重要建模方法,即基于概率α分位和神经网络(neural network,NN)的区间回归分析方法.针对含噪声工业时间序列数据,文献[14]再次将NN与概率分位数方法相结合,提出了工业数据的区间模型预测方法.对于前一种方法[11],首先从已知的不确定性数据中建立数据的主要变化趋势,再引入α分位分别获取区间模型的上、下界模型.后一种的区间模型分别用上界g∗(x)和下界g∗(x)模型来描述,求解过程仍然采用传统的反向传播(back propagation,BP)方法.众所周知,NN在模型结构选择上存在主观性较大、复杂,以及参数求解主要是基于最小二乘的目标优化,导致较差的模型泛化性能.近年来,基于结构风险最小化的支持向量机(support vector machine,SVM)成了重点关注,在模式识别和函数逼近问题上得到了成功的应用,文献[4,15–16]提出了基于支持向量学习方法的模糊回归分析,该方法较传统神经网络方法做了较好的改进.

进一步,考虑到基于SVM的回归模型求解存在两个问题:1)从SVM中非线性映射的大规模数据中求解有一定的困难;2)不同样本数据集间的大小不平衡,往往出现一个类的样本集比另一样本集大,引起分割间隔的偏移.因此,针对上述问题,文献[17]提出了简化SVM的区间回归分析方法来减小支持向量(support vector,SV)的个数,然而在提出的方法中是通过将L1范数的结构风险与逼近误差的L∞范数相结合来实现.此外,文献[18]从应用的角度出发,通过将获取到的确定性测量数据(单值)转换为区间描述,建立了基于非参数加性模型的区间回归分析方法,正确实现区间测量数据可能的非线性模式识别.针对区间数据现有的回归分析使用确定的数据参考点再加上半径范围来建立区间的上、下界方法存在一定的限制,例如不同的数据集应该考虑采用不同的数据参考点描述区间,文献[19]提出了如何更好地从回归变量中提取最佳参考点的参数化方法.此外,从区间数据的另一个角度出发,当区间数据出现异常值的情况时,文献[20]对区间值变量的的指数核鲁棒回归模型进行了研究,通过指数型核函数的使用,对区间值观测值中的异常值引入权值进行惩罚,进而保证了参数估计算法的收敛速度以及较低的计算成本.从提高模型建模精度出发,文献[21]将概率分位与群体智能化方法相结合对参数进行估计,并论证了方法的有效性与优越性.

在本文中,建立了一种新的区间回归模型辨识方法:1)基于文献[22]提出了最小化最大逼近误差的L∞范数引理,作为分别建立区间模型的上、下边回归模型优化问题的基础;2)提出了基于L1范数框架下的结构风险最小化的代价函数,在保证辨识区间回归模型精度的同时,尽可能对模型结构复杂性进行有效控制,进而提高模型的泛化性能;3)基于引理1,提出了独立求解上、下边回归模型的两个定理,并应用简单线性规划对其求解.

2 凸二次规划到线性规划的支持向量回归

2.1 凸二次规划的支持向量回归

由Vapnik及其团队所建立的SVM[23–24]很好的克服了传统过拟合的分类问题.因此,在SVM中引入不敏感损失函数可发展为非线性的回归问题,即支持向量回归(support vector regression,SVR),已在最优控制[25]、时间序列预测[26]、区间回归分析[27]等方面得到了广泛应用.假设通过传感器或其他数据获取设备获取到一组带有噪声的测量数据{(x1,y1),(x2,y2),···,(xN,yN)},SVR方法是对这组数据所对应的未知数学模型进行逼近,其中xk=(x1k,x2k,···,xdk)表示d维的输入模式.假设一组线性无关的基函数{ωs(x),s=1,···,m},可用基函数的线性展开描述任意的非线性系统.因此,函数的逼近问题可转化为寻求如下基函数线性展开的最优参数求解[24]:

其中:θ=(θ1,θ2,···,θm)为需要被寻优的参数向量;b是一个常量.进一步,该问题的参数寻优即为寻找满足如下优化问题的非线性函数f:

R(f)为结构风险;γ表示规则化常量,体现对模型结构与建模精度重视程度的权衡;的引入在于控制模型的复杂度;Lε(·)为描述ε不敏感损失函数,定义为

从上述ε域定义可知,如果|yk −f(xk)|的值在该ε区域内,损失为0;否则为|yk −f(xk)|与ε的差值.

通过应用拉格朗日乘子方法,对式(2)的最小化可转化为它的对偶优化问题[28]:

核函数确定了解的平滑特性,选取时应该更好的反映数据的先验知识.式(4)的优化问题可重写为

其中常量b的计算为

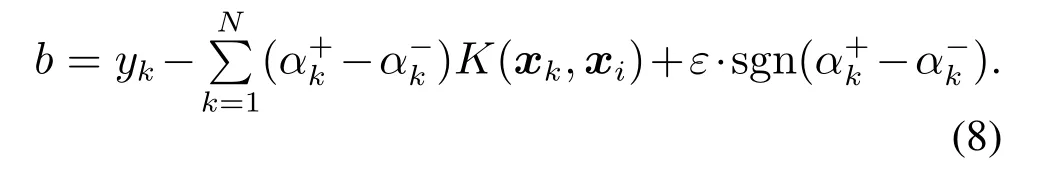
σ为高斯核参数.

2.2 SVR的优化问题转化

众所周知,SVR是将基于二范数的结构风险最小化作为优化目标,实现对回归模型结构复杂性的控制,从而提高模型的泛化性能;然而,在文献[29]中指出,SVR中的优化目标求解采用的是二次规划,会产生模型的冗余描述以及昂贵的计算成本;同时,二范数的优化问题不能直接用于本文提出的最优区间回归模型辨识的优化问题,需要进行二范数到一范数的转化.对于二次规划(quadratic programming–SVR,QP–SVR)[30],基于式(2)的优化问题如下:

其中:ψ(·)表示从输入空间到高维空间的非线性特征映射,即ψ:Rn −→Rm(m>n);ξk,为松弛变量,分别对应超出正、负方向偏差值时的大小;常量γ大于0,反应非线性f与偏差大于ε时两者之间的平衡.对于式(9),令βk=α+k −α−k,则有

β=(β1β2··· βN)T.考虑到式(2)的优化问题,范数的引入是为了控制模型的复杂度,根据范数的等价性可知,在结构风险中引入其他范数也可以同样对模型复杂性进行控制[31].接下来,将QP–SVR的优化问题(10)变成

其中:f(xk)以式(9)形式描述;∥β∥1表示系数空间的1–范数.因此,新的约束优化问题为[32]

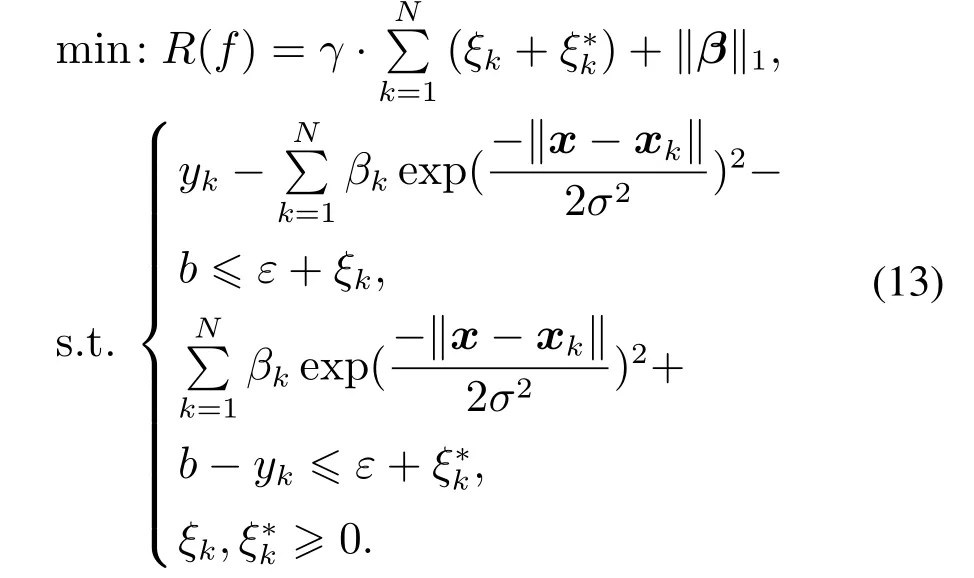
为了转化上述优化问题为线性规划问题,将βk和|βk|进行如下分解[32]:

基于式(15),优化问题(14)进一步变成

现定义向量

和向量β的L1范数

以向量形式将优化问题(16)构造为线性规划问题

其中:ξ=(ξ1ξ2··· ξN)T;I为N ×N单位矩阵;

线性规划问题(19)可通过单纯型算法或内点算法进行求解[33].对于QP–SVR,在ε域之外的所有数据点将被选择为支持向量(SV);而对于LP–SVR,即便ε域选择为0时,由于软约束在优化问题中的使用,LP–SVR仍然能够获取稀疏解.通常情况下,稀疏解往往通过设定非零的ε域来获取.

3 基于逼近误差的L∞范数的回归模型辨识

回归模型的辨识离不开参数的求解,为了能够将控制模型结构复杂性控制的优化问题应用到回归模型辨识,下面将讨论将基于逼近误差的L∞范数作为评判标准,建立回归模型辨识的优化问题.假设通过传感器或数据获取设备获取一组测量数据{(x1,y1),(x2,y2),···,(xN,yN)},其中{x1,x2,···,xN}描述输入测量数据,对应的输出定义为{y1,y2,···,yN}.设测量满足如下非线性系统模型:

根据统计学理论可知[34],存在以式(11)描述的非线性回归模型f对测量模型g的任意逼近,当逼近精度越小时,需要的支持向量越少;反之,逼近精度越高,则支持向量越多.因此,对任意给定的实连续函数g及η >0,存在如下回归模型f满足:

值得指出的是,较小的η值,对应式(11)较多的支持向量.现讨论回归模型,式(11)的另一种参数求解方法.在非线性系统模型的逼近情况下,定义实际输出与由式(11)定义的SVR模型输出之间的偏差ek:

为了估计SVR模型的最优参数,考虑如下最大建模误差的最小化:

Z表示整个输入数据集.显然,这是一个最小–最大(min-max)优化问题.在式(11)描述的回归模型情况下,式(23)的最小化可通过如下两个阶段完成:1)核函数中的核宽度σ的参数寻优,通常采用经典的k阶交叉验证或其他优化方法来实现;2)式(11)的参数确定可通过min-max优化问题求解,即

基于文献[22],优化问题(24)可通过如下引理1求解,该引理也是本文提出方法用于辨识最优区间回归模型的基础.

引理1min-max优化问题中的参数可通过最小化λ,且满足如下不等式约束的线性规划求解,即

其中:β=(β1β2··· βN)T和b为被求解参数,λ表示最大逼近误差.

证定义λ如下:

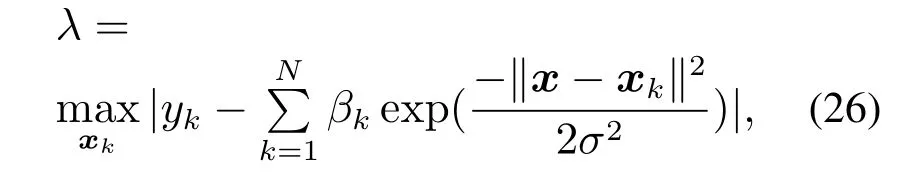
可直接得出如下不等式成立:

根据去绝对值运算,可知式(1)的约束条件成立.

证毕.

4 基于L∞范数区间回归模型辨识

有了基于L∞范数的回归模型辨识的基础之后,接下来将讨论区间回归模型的辨识的一种新方法,为了能给出辨识方法的清晰思路,整个辨识过程如图1所示.

假设不确定非线性函数或非线性系统属于某函数簇Γ,由名义函数g和不确定性∆g(x)两部分组成,即

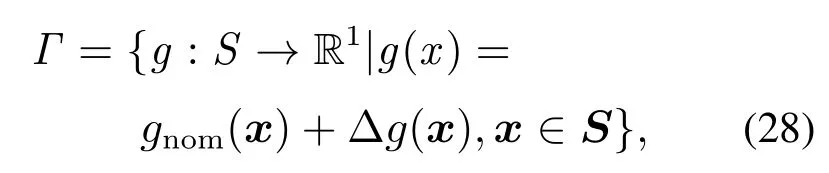
gnom为标称函数,不确定性∆g(x)满足

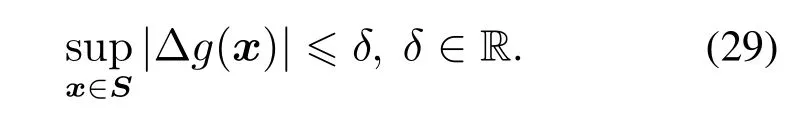
现考虑来自函数簇Γ的成员函数g,x ∈Rd,对应输入x上的测量输出Y={y1,y2,···,yN},即yk=g(xk),g ∈Γ,xk ∈S,k=1,2,···,N.最优区间回归模型辨识的思想是,在满足如下约束条件(30)的情况下,辨识下边回归模型fL(xk)和上边回归模型fU(xk):

在上式约束的意义下,来自函数簇的任一成员函数总能在区间带[fL(xk),fU(xk)]中找到.这样的区间带有无穷多个,本文的目的就是根据提出的约束,确定尽可能窄的区间带.该问题的研究,文献[35]采用了连续分段线性函数的逼近方法来实现.在本文,是通过最小化最大逼近误差来给出回归模型更好的逼近,或寻找一个更紧凑的逼近带.基于式(11),可给出上、下边回归模型的表达式如下:

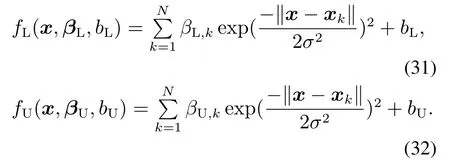
基于引理1,式(32)和式(31)所对应的上、下边回归模型fU(x),fL(x)可通过线性规划对如下优化问题进行求解.

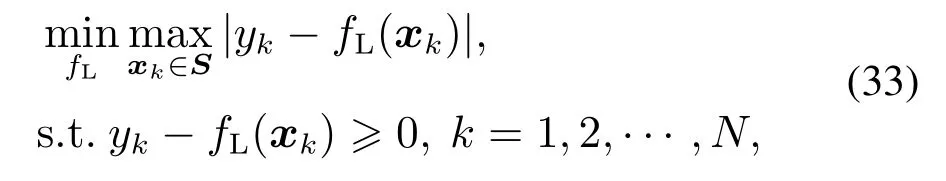
因此,进一步可得如下定理.

定理1对于下边回归模型fL(x)的参数βL,bL的求解,对应min-max优化问题(34)可通过最小化λ1,且满足如下不等式约束的线性规划求解,即

λ1表示对应下边模型fL最大逼近误差.

图1 一种新的区间回归模型辨识方法流程图Fig.1 Flow chart of identifying interval regression model using proposed method

定理2对于上边回归模型fU(x)的参数βU,bU的求解,对应min-max优化问题(34)可通过最小化λ2,且满足如下不等式约束的线性规划求解,即λ2表示对应上边模型fU最大逼近误差.

证上述定理1和定理2可直接通过引理1推出.

证毕.

从上述区间回归模型辨识的思想来看,仅考虑如何让上、下边模型输出与实际输出之间的逼近误差最小,而对回归模型本身的结构复杂性控制却没有被考虑,这样一来,通过上述优化问题获取的参数解有可能出现不全为零的情况,不具有稀疏性,对应N个样本数据可能对区间模型的建立都在起作用,从而导致较复杂的模型结构.为了解决模型稀疏解的问题,在求解区间回归模型的优化问题中,有必要将结构风险最小化的思想融合其中,在保证回归模型逼近精度的同时,尽可能让模型结构复杂性得到有效控制.基于此,将区间回归模型所对应的上、下边回归模型优化问题(35)和(36),融合到基于结构风险最小化的优化问题(16).因此,基于式(15),对应下边回归模型新的优化问题为

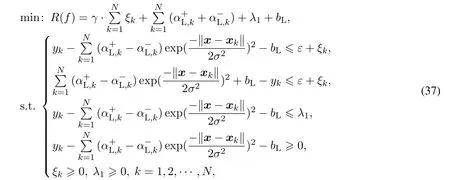
其中λ1表示最大逼近误差,参数与第2节的定义一样.

对于上边回归模型fU(x)的优化问题,有

相似地,λ2表示最大逼近误差,参数,bU,ε,ξk与第2节的定义一样.从优化问题(37)和(38)可知,为典型的线性规划问题,可用向量及矩阵形式表述如下:

以及

其中:I为N×N单位矩阵,Z表示N阶零矩阵,E和0是元素分别为1和0的列向量,

核矩阵K的元素定义为

σ为可调核参数.显然,应用内点法或单纯性方法可以求解优化问题(40)和(39),进而得到区间回归模型所对应的上、下边回归模型fU(x)和fL(x):

从提出的优化问题中来建立fU(x)和fL(x)的整个过程来看,优化问题既包括了对模型结构复杂性控制的目标函数,又包括了如何获取较好的模型精度所对应的逼近误差作为目标函数,而且模型结构复杂性和模型精度之间的权衡可以通过超参数(包括核宽度、规则化参数以及不敏感域)进行调整.如果超参数选取不当,会极大影响所建立区间模型的泛化性能.当前,关于超参数寻优的方法包括元启发式算法[36]、k–阶交叉验证法[37]、正弦–余弦算法(sine cosine algorithm SCA)[38]、遗传算法(genetic algorithms)[39]、粒子蠕优化算法(partical swarm optimization,PSO)[40]等.然而,在众多参数寻优方法中,k–阶交叉验证法可以较好的避免模型过拟合问题[37],在理论研究和实际应用中得到了广泛应用.总而言之,提出方法在保证获取区间模型尽可能窄的区间带的同时,而且还对模型结构复杂性进行有效控制,从而提高区间回归模型的泛化性能[41].因此,k–阶交叉验证法将用于本文的参数寻优,其原理为:1)首先将整个训练集划分为k个互斥且大小相同的子集,其中一个作为测试集,剩下的k −1个作为训练集;2)将被寻优的参数对(核宽度σ、规则化参数γ)以递增方式设定,例如σ=2−15,2−13,···,23,γ=2−5,2−3,···,215;3)再用提出的方法以及参数对分别建立上、下边回归模型fU(x)和fL(x).这样一来,训练集中的每个样本都将被用于模型的一次预测得到相应的预测值,并与真实值比较形成交叉验证精度;4)将最好的交叉验证精度所对应的参数对作为区间模型的最优参数选择.

所建立的区间回归模型可以用于系统的故障检测,例如当系统运行在健康状态时,获取所对应的无故障数据,应用提出的方法对无故障数据进行建模,得到相应的区间回归模型,从而获取系统健康状态下的区间带.在系统运行期间,检测某个测量参数输出是否包含于区间带,若实际输出在对应的区间带内,则判断系统运行正常,否则故障发生;此外提出的区间回归模型也可用于鲁棒控制设计、信息压缩等方面.

5 实验研究

这部分内容将通过如下实验分析,论证所提出方法的最优性与稀疏性;同时为了更直观的去评判提出的方法,将考虑如下两个性能指标,即均方根误差(root mean square error,RMSE)和支持向量占整个样本数据的百分比SVs%.对于RMSE 指标定义如下:

N表示测试数据的总数,yk为实际输出,ˆyk是模型的被估输出.RMSE反映了用提出方法所建立区间回归模型在满足各自约束条件下,即fU(x)−y≥0以及fL(x)−y≤0,模型输出与实际测量数据之间的逼近程度;RMSE越小,逼近程度越好,反之越差.此外,对应优化问题(39)–(40)的求解,若有或,则对应第k个样本数据为支持向量,假设通过该条件判断获取Nk个支持向量,则支持向量(SV)占整个样本数据的百分比SVs%可定义如下:

显然,在保证模型精度的同时,指标SVs%越小越好,越小则表示求解的区间模型有稀疏解,模型结构简单,具有较好的泛化性能.

下面将对提出的方法从区间模型的辨识精度以及稀疏特性展开实验分析,论证其合理性与优越性,包括不受噪声干扰、受噪声干扰的不确定性测量数据以及参数的不确定性.其中是支持向量回归理论[30]产生以来,以及用于论证其他方法[42]最常采用的仿真.

首先考虑sinc(x)无噪声情况下的分析,在区间[−10,10]上获取100个等间隔无噪声样本.采用5–阶交叉验证法[37]获取参数集(ϵ,γ,σ)为(0.0001,1000,2.8),再通过提出的方法建立最优区间回归模型如图2所示,图3 给出了URMfU(x)和LRMfL(x)的逼近误差.从图2可知,区间模型与无噪声的实际输出基本上重合,fU(x)与fL(x)无限逼近实际输出.与其他方法相比较,提出的方法分别需要12 个支持向量(SV)建立区间模型的fU(x)和fL(x),模型预测输出与实际输出之间的最大误差为0.0057 和0.0108;文献[34]用了39个SV,最大误差0.01;文献[42]用了9个SV,最大误差为0.0087.因此,无论从模型稀疏特性还是建模精度来看,提出的方法具有一定的优越性.此外,当被建模对象无噪声干扰时,提出的最优区间回归模型变成了传统的确定性建模.

图2 提出方法的区间输出Fig.2 The output of IRM

图3 URM和LRM的逼近误差Fig.3 Approximation error with noise-free for URM and LRM

接下来,考虑sinc(x)受噪声干扰的情况.类似地,在区间[−10,10]上获取100 个带均匀分布噪声为[−0.2,0.2]的等间隔噪声样本.应用5–阶交叉验证法[37]获取设超参数集(ϵ,γ,σ)为(0.01,100,2.5),则sinc(x)的区间输出逼近如图4所示,URM和LRM分别从100个数据中,仅仅用了其中的10 和9个数据建立回归模型,这些数据被称SV,对应的SVs%则为10%和9%,反映了提出方法所建立区间模型的稀疏特性;RMSE为0.1291和0.1238反映了建立区间模型的精度.

图4 提出方法对100个噪声样本建立的区间输出Fig.4 The output of IRM corresponding to 100 noise samples using the proposed method

从建模精度指标RMSE的数值来看,尽管所反映的区间带变宽,紧凑性变差,但模型具有较好的稀疏特性.因此,建模精度与模型稀疏特性是一对矛盾体,根据建模的需要,从两者之间取其平衡.继续对sinc(x)在相同噪声作用下,产生1000个样本建立区间模型,仍然采用超参数集(ϵ,γ,σ)为(0.01,100,2.5),图5给出了提出方法的区间输出,在保证模型精度条件下,稀疏特性也进一步得到保证,例如URM和LRM分别从1000个数据中,仅用了13和12个数据,对应的SVs%为1.3%和1.2%,RMSE为0.2264 和0.2301.图6给出了IRM 的逼近误差,其中fU(xk)−yk≥0 以及fL(xk)−yk≤0.

图5 提出方法对1000个噪声样本建立的区间输出Fig.5 The output of IRM corresponding to 1000 noise samples using the proposed method

图6 区间模型的逼近误差Fig.6 Approximation error with noise-free for URM and LRM

为了进一步论证提出方法的稀疏特性,在实验仿真过程中,事先设定大于0的较小值η=1.0×108,判断回归模型的展开项中系数,k=1,2,···,N是否成立,如果满足该条件,说明展开项中的第k项对回归模型起作用,对应第k个样本xk为支持向量,如图7–8所示,分别对应URM和LRM中.

图7 对应LRM展开项系数Fig.7 The coefficient of expansion term for LRM corresponding to(where δ is selected as 1.0E–08 in computational simulation)

图8 对应URM展开项系数Fig.8 The coefficient of expansion term for URM corresponding to(where δ is selected as 1.0E–08 in computational simulation)

继上述来自测量数据的不确定性实验分析后,下面考虑来自模型参数不确定性的最优区间模型辨识.假设带有不确定性参数的非线性函数类Γ,其成员函数为f(x),由名义函数fnom(x)和不确定性∆f(x)构成,即

设该函数类的定义域为−1 ≤x≤1,为获取建立模型所需要的样本数据,不妨取xk=0.021k,k=−47,−46,···,46,47,图9给出了由不确定性参数τ引起的不确定性输出.接下来用提出的区间回归模型包络由不确定性参数τ值所引起的测量输出.应用5–阶交叉验证获取超参数集(ε,γ,σ)为(0.001,100,3.5),由上边、下边模型构成的区间回归模型如图10所示,区间模型的曲线平坦度变化相对较大,分别对应URM与LRM的SVs%都为45.26%,RMSE为0.0037和0.0036,辨识精度进一步提高,但区间模型趋于复杂,其中点线属于Γ;若选取(ε,γ,σ)为(0.001,100,4.5),如图11 所示,fU(x)和fL(x)的RMSE 分别为0.0073和0.0074,反映了提出方法的辨识精度较图10模型结构相对简单,此时URM与LRM从96个数据中,仅用了21个数据(支持向量)建立区间模型的上、下边界(对应SVs%都为22.11%),稀疏特性较好,曲线较平坦,实线分别对应上边回归模型逼近fU(x)以及下边回归模型逼近fL(x).换言之,图11所对应区间模型的稀疏特性比图10好,但辨识精度却比图10差.此外,图12 和图13 给出了在满足各自约束条件的fU(x)和fL(x)的逼近误差曲线.为了更清晰的论证提出方法在辨识精度和稀疏特性之间的平衡,表1和图14在不同核参数情况下的两个指标RMSE和SVs%的变化,分别反映了模型辨识精度及模型的稀疏特性.

图9 由参数不确定性引起的非线性函数簇输出Fig.9 Actual of the family of nonlinear function caused by the uncertain parameter τ

图10 当核宽度选择为3.5时所对应的的区间输出Fig.10 The output of IRM when the kernel width is selected as 3.5

图11 当核宽度选择为4.5时所对应的的区间输出Fig.11 The output of IRM when the kernel width is selected as 4.5

图12 区间模型的逼近误差Fig.12 Approximation error for URM and LRM

图13 区间模型的逼近误差Fig.13 Approximation error for URM and LRM

图14 RMSE与SVs%在不同核宽度下的比较结果Fig.14 Comparison results both RMSE and SVs%with the different σ is shown for URM(left)and LRM(right)

进一步,将提出的方法与文献[15]从两个指标RMSE,SVs%进行分析比较.根据文献[15]定义如下回归估计量:

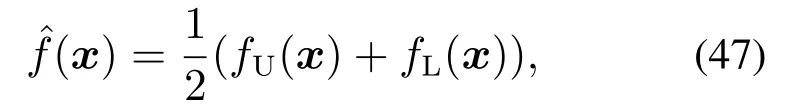
则有回归估计的均方根误差为

N表示测试数据的总数,f(x)为实际输出,是模型的被估输出.值得注意的是,该式的定义与式(43)是不一样的,式(43)描述的是fU(x)和fL(x)与不确定性数据之间的RMSE,而式(48)描述的是回归估计量的RMSE.在文献[15]中,下面的非线性系统仿真被考虑:

其中noise表示在区间[−1,1]上随机产生的实数.从式(48)分别获取训练数据和测试数据,当应用5–阶交叉验证获取超参数(ε,γ,σ)为(0.001,10,0.5)时,应用提出的方法所建立的区间模型以及对应的上、下边回归模型的逼近误差分别如图15–16所示,上、下边回归模型从51个数据中都用了4个SV.对于fU(x)(上边回归模型),对应的第k个SV以及值如表2所示,其表达式为

图15 当核宽度选择为0.5时所对应的区间输出Fig.15 The output of IRM when the kernel width is selected as 0.5

图16 当核宽度选择为0.5时所对应的区间输出逼近误差Fig.16 The approximation error of IRM when the kernel width is selected as 0.5

表2 fU(x)所对应的第k个SV以及值Table 2 The kth SV with

表2 fU(x)所对应的第k个SV以及值Table 2 The kth SV with

同理,对于fL(x)(下边回归模型),对应的第k个SV以及值如表3所示,其表达式为

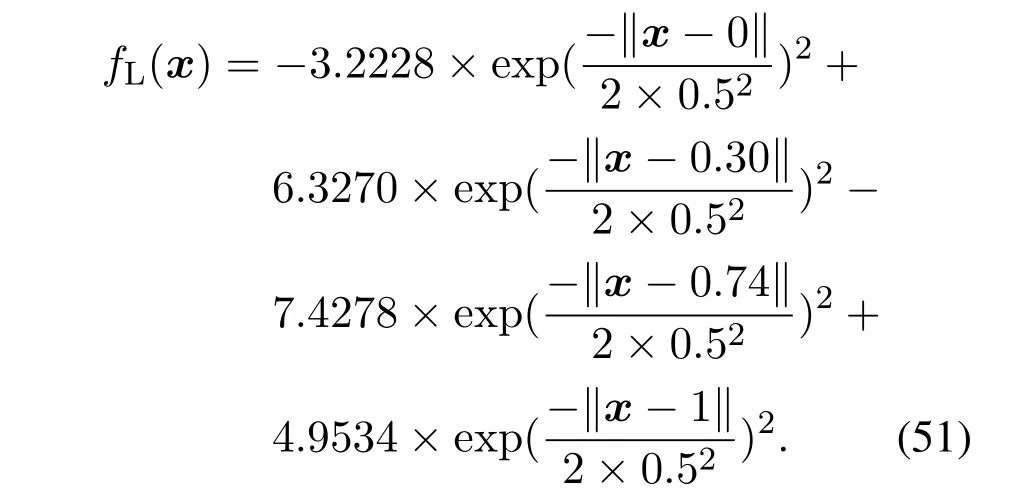
表3 fL(x)所对应的第k个SV以及值Table 3 The kth SV with

表3 fL(x)所对应的第k个SV以及值Table 3 The kth SV with

当超参数(ε,γ,σ)的选取与文献[15]一样时,即(100,0.03,0.18),所对应的RMSE 和SVs%如表4 所示,无论是从训练还是测试RMSE,提出方法的建模精度较文献[15]的好,而且模型结构也较稀疏,对应SVs%为15.68%.

表4 本文提出方法与文献[15]的比较Table 4 Comparison results of the proposed method and[15]

因此,通过上述实验对提出的两个指标,即SVs%以及RMSE进行分析可知,提出的方法可以:1)很好的建立来自不确定性测量数据或系统模型参数不确定性的区间模型,采用区间输出代替传统的点输出建模方法,更易于实际问题的研究;2)很好的解决了模型结构复杂性与辨识精度之间的平衡,在提高模型泛化性能的同时,模型辨识精度也能得到保证.

6 结论

当获取一组由测量或参数不确定性等因素导致的测量数据集时,提出了一种新的区间回归模型辨识方法.该方法将结构风险最小化理论与逼近误差的L∞范数最优化思想相结合,给出了在保证被辨识模型精度条件下,对模型结构复杂性进行有效控制的目标优化问题,同时将复杂的凸二次规划求解转化为较简单的线性规划问题求解.克服了传统方法在辨识非线性系统过程中,目标优化问题仅考虑模型输出与实际输出之间的偏差达到最小,致使模型结构复杂.提出的区间回归模型由包含所有测量数据的上、下边回归模型构成,可应用于被观测系统的参数在某个区间变化时的函数簇建模、也可用于数据挖掘中的信息压缩、鲁棒控制系统辨识以及故障检测.