线电感特征点定位的开关磁阻电机无位置传感器控制方法

匡斯建,张小平,刘 苹,张光辉,张 铸

(1.湖南科技大学海洋矿产资源探采装备与安全技术国家地方联合工程实验室,湖南湘潭 411201;2.湖南科技大学信息与电气工程学院,湖南湘潭 411201)

1 引言

开关磁阻电机(switched reluctance motor,SRM)具有成本低、结构简单、可靠性高、容错能力强等系列优点[1],目前已在纺织机械、矿产开采等诸多领域得到了大量应用[2].而要实现开关磁阻电机的高精度调速控制,就必须准确获取其转子的实时位置信息.传统获取转子位置信息主要利用位置传感器,但这种方式不仅增加了调速系统的体积、成本及加工复杂度,同时也降低了调速系统在一些特定环境下的工作可靠性.因此开展开关磁阻电机无位置传感器研究具有重要的现实意义[3].

近年来,国内外在有关开关磁阻电机无位置传感器控制方面已开展了大量研究,提出了诸如电感模型法[4–6]、智能算法[7–9]及磁链–电流法[10–13]等多种无位置传感器控制算法.其中电感模型法通过预先将电机相电感、电流及对应的转子位置存储于三维表格中,在电机运行时只需通过实时采集电机的电流值并进行简单的运算处理,即可根据该数据表获得相应的转子位置角度:该算法原理简单,但占用系统资源大、灵活性和实时性不高.智能控制法是通过建立以电流和磁链为输入、转子位置角度为输出的非线性映射模型,再根据该模型并通过实时采集电流和磁链值来估算出转子的位置角度:该方法位置估算精度高,但存在算法复杂、运算工作量大等不足.磁链/电流法则是通过对开关磁阻电机导通相施加斩波控制电流及非导通相施加高频检测脉冲,再利用导通相与非导通相电感交点的位置角度来对电机的转子位置进行估算:该算法具有占用系统资源较少、运算工作量适中等优点,但在导通相电流大于其临界饱和电流后,上述相电感的交点位置会随导通相电流的增大而发生偏移,从而导致在估算电机转子位置时会产生较大的偏差.

针对磁链/电流法存在的上述不足,本文提出一种线电感特征点定位的开关磁阻电机无位置传感器控制方法,取得了满意的效果.首先给出线电感及其特征点的基本概念,推导基于线电感特征点确定开关磁阻电机转子位置角度的具体实现方法,并通过仿真和实验对该方法的正确性进行验证.

2 开关磁阻电机全周期电感分析

本文以三相6/4 结构开关磁阻电机为例,设各相绕组的参数一致,则各相绕组电感随转子位置角度的变化规律相同,只是相位错开一定的角度.在磁路非饱和的情况下,三相绕组电感LA,LB和LC随转子位置角度θ的变化曲线如图1所示.可见,在一个机械周期90°内,三相电感曲线有6个交点,其交点角度分别为15°,30°,45°,60°,75°和90°,在磁路达到临界饱和之前,上述各交点的位置角度基本不变.

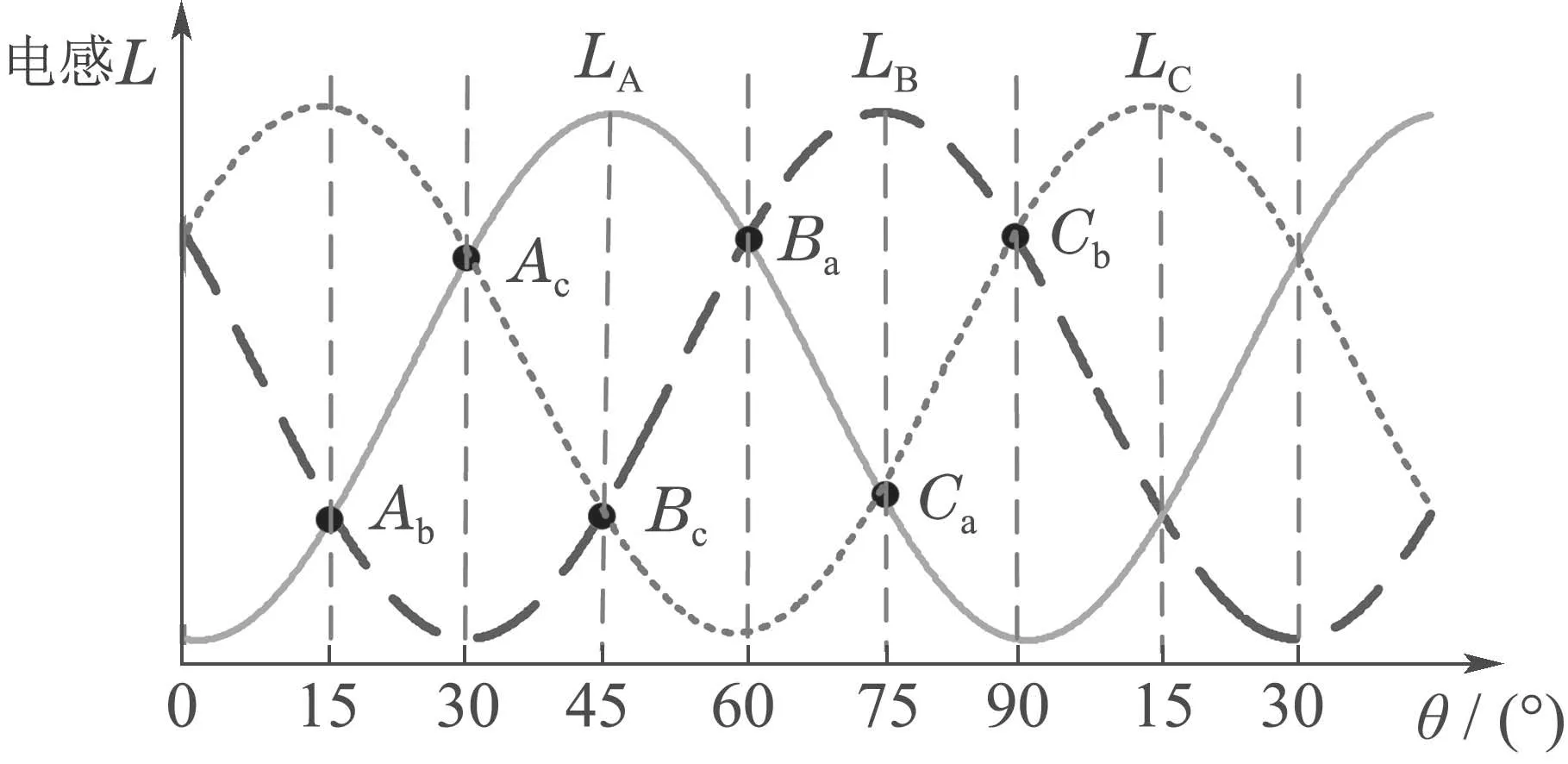
图1 三相绕组电感随转子位置角度的变化曲线Fig.1 Curve of three phase winding inductance varyingwith rotor position angle

然而在电机实际运行中,其导通相磁路会随导通相电流的增大而逐渐趋于饱和,从而使导通相电感曲线随导通相电流的增大而发生变化.以A相为导通相,B,C相为非导通相为例,其导通相与非导通相电感曲线交点随导通相电流的变化关系如图2所示.可见,在A相电流小于或等于其临界饱和电流9 A时,A相电感曲线基本无变化,它与B,C相电感曲线的交点位置也基本不变:而当A相电流大于临界饱和电流9 A后,随着A相电流的逐步增大,其电感值将逐步减小,因而其电感曲线将逐步下移,从而导致该电感曲线与B,C相电感曲线的交点也随之逐步下移.由此可见,当导通相电流大于其临界饱和电流后,若仍按照磁路非饱和时的相电感交点位置角度来估算电机转子的位置角度,则会造成较大的误差.

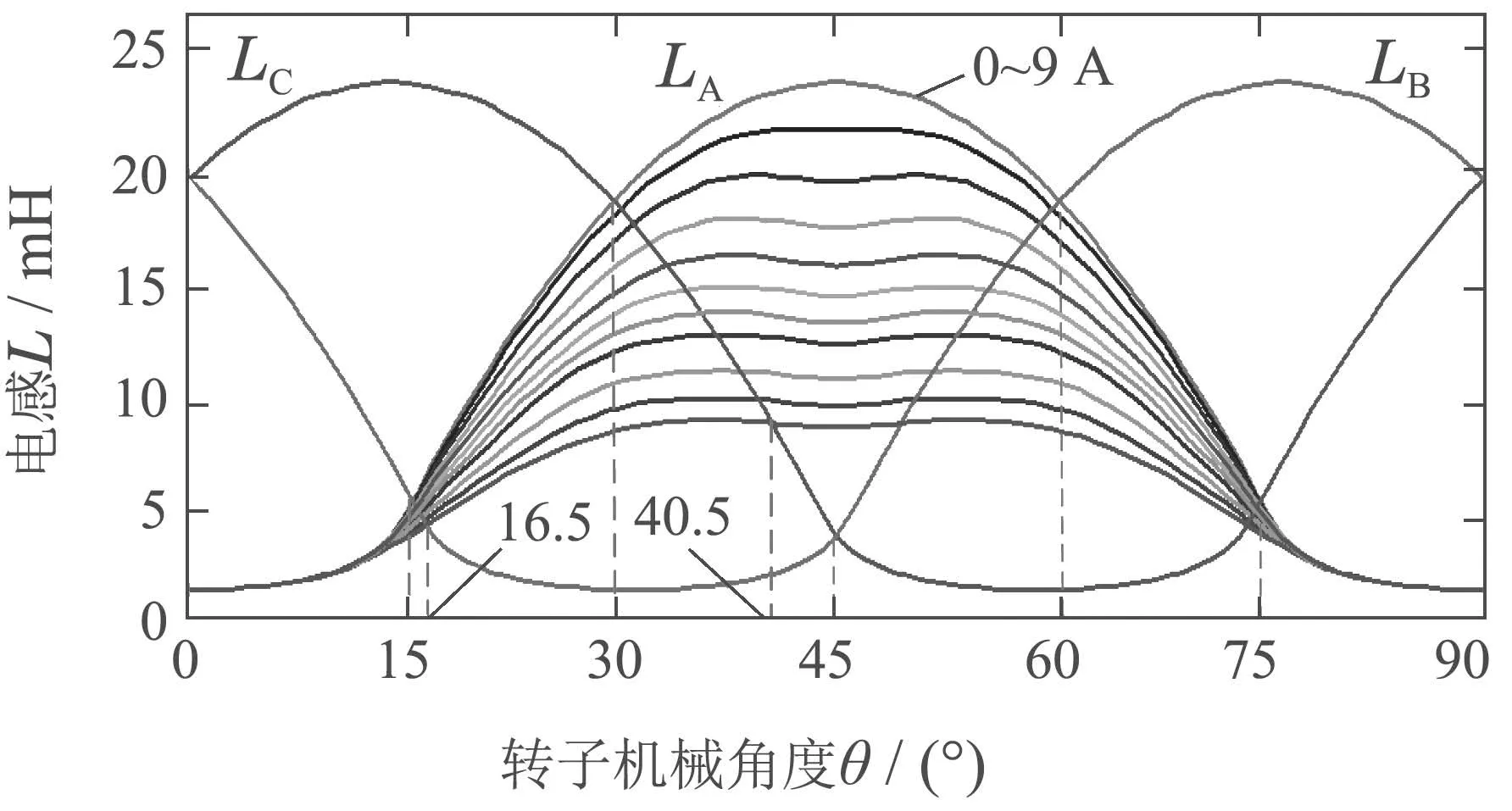
图2 导通相与非导通相电感交点随导通相电流变化曲线Fig.2 The change diagram of the intersection point between the conduction phase and the non conduction phase inductance curve with the conduction phase current

3 开关磁阻电机相电感函数

根据上述开关磁阻电机的电感分析,本文提出基于线电感特征点来确定开关磁阻电机的转子位置角度,为此首先确定相应的线电感函数:而要确定线电感函数,又必须预先确定电机各相绕组的相电感函数:根据文献[14],三相开关磁阻电机相电感可由式(1)所示斜率差法获得:

式中:udc为直流母线电压;∆i为开关管导通与关断期间的相电流斜率差.

根据式(1)可计算出开关磁阻电机全周期内不同位置角度的一系列电感值,采用数值拟合方法可得到相应的相电感函数关系式,其傅里叶级数形式的展开式可表示为[15]

式中:Nr表示转子级数;Ln(i)表示基波及各次谐波项的系数函数;φn表示初相位.

以三相开关磁阻电机为例,在一个转子电气周期内,将开关磁阻电机第一个导通相称为A相,随后导通相称为B相,最后导通相称为C相.为简化分析计算,忽略式(2)中的高次项后,可得三相开关磁阻电机各相简化电感函数分别为[15]

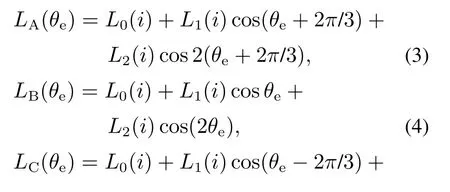
式中:LA(θe),LB(θe),LC(θe)分别表示三相开关磁阻电机A,B,C相的电感函数;θe表示电机转子的电气角度;L0(i),L1(i)和L2(i)分别表示相电感各分量的系数函数,各系数函数的计算方法可参考文献[15].

4 开关磁阻电机线电感函数及其特征点性质

本文将开关磁阻电机两相邻相绕组电感函数之差定义为该两相邻相绕组的线电感函数.因而对于三相开关磁阻电机来说,其相应的线电感函数可分别表示为

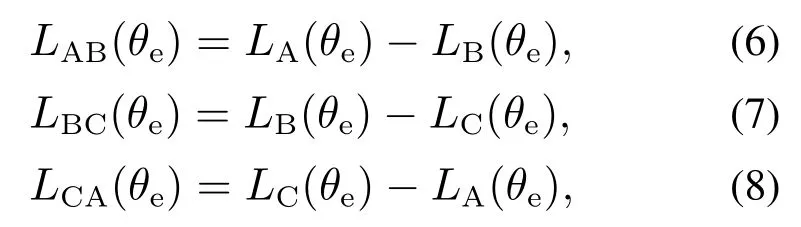
式中:LAB(θe)表示开关磁阻电机A,B相绕组间的线电感函数;LBC(θe)表示B,C相绕组间的线电感函数;LCA(θe)表示C,A相绕组间的线电感函数.

将式(3)–(5)代入式(6)–(8)中,可得三相开关磁阻电机线电感函数的具体表达式为

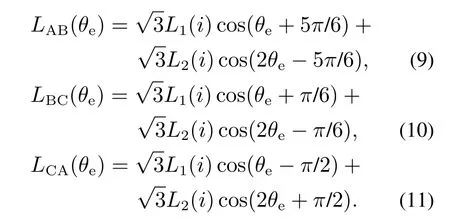
根据式(3)–(5)及式(9)–(11),可得三相开关磁阻电机相电感及线电感曲线如图3所示.

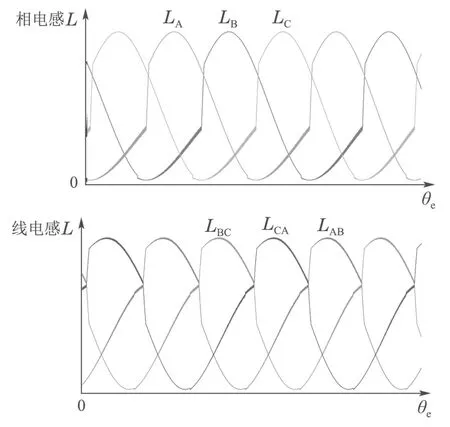
图3 三相开关磁阻电机相电感及线电感曲线示意图Fig.3 Schematic diagram of phase inductance and line inductance of three phase switched reluctance motor

同时,根据式(9)–(11),可得如下等式:

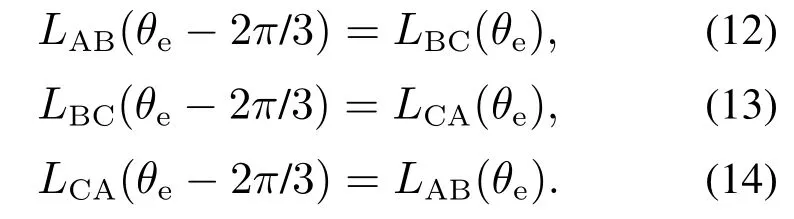
可见,线电感LBC(θe)滞后于LAB(θe)的相位角为2π/3,同理,LCA(θe)滞后于LBC(θe)及LAB(θe)滞后于LCA(θe)的相位角也等于2π/3,也即当三相开关磁阻电机的线电感值相等时,各线电感所对应的转子电气角度间均相差2π/3,且与相电流大小及相电感系数函数L0(i),L1(i)及L2(i)的取值无关.因此本文将线电感值相等时所对应的转子位置点(θe,L(θe))定义为特征点,如图4所示.根据特征点定义,可取任意线电感值相等时所对应的位置点作为特征点:实际应用中为方便起见,可取线电感的交点作为特征点,如图5 所示.图5中线电感交点包括线电感值小于0的负值交点和线电感值大于0的正值交点,本文在进行转子位置角度估算时采用线电感正值交点.

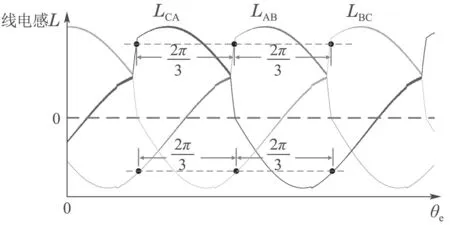
图4 线电感特征点位置关系示意图Fig.4 Schematic diagram of location relation of line inductance characteristic points

图5 线电感交点示意图Fig.5 Schematic diagram of line inductance intersections

根据上述有关线电感特征点的定义及性质可知,三相开关磁阻电机两相邻线电感特征点之间的电气角度∆θe均为2π/3,再根据电机转子机械角度与电气角度间的关系,可得对应的机械角度为

式中:∆θn表示两相邻线电感特征点间的机械角度;Nr表示电机转子极数.如对于三相6/4结构的开关磁阻电机来说,其Nr为4,则∆θn为π/6.

5 转子位置估算方法

根据上述确定的两相邻线电感特征点间的机械角度,如进一步确定电机转子转过上述两特征点对应区间的时间,则可确定电机转子在上述区间的平均转速,再根据该平均转速即可对电机转子在下一对应区间的位置角度进行估算.

5.1 两相邻线电感特征点对应区间时间确定方法

以图5中两相邻特征点X2与X4为例,介绍其对应区间时间的确定方法,具体为:当系统控制器捕获到特征点X2时,将控制定时器清零并启动定时器开始计时,同时检测下一相邻线电感的实际值,当下一个相邻线电感的实际值等于特征点X4的电感值时,记录并保存定时器中的时间值∆t1,该时间值即为两相邻线电感特征点X2至X4对应区间的时间:然后将定时器清零并重新启动定时器计时,继续检测下一相邻线电感特征点X6的出现并记录对应区间的时间∆t2,如此周而复始,从而可获得所有相邻线电感特征点对应区间的时间值∆tn.

5.2 转子转速与位置角度确定方法

根据上述检测的两相邻线电感特征点对应区间的时间∆tn,同时根据该区间的机械角度30°,即可计算出电机转子在该区间内的平均转速,即

鉴于开关磁阻电机属惯性负载,因而当其转子从第n个区间旋转至第(n+1)个区间时其转速可认为基本保持不变,为此可根据电机在第n个区间的平均转速,估算出电机转子在下一个对应区间,即第(n+1)个区间任意时刻的位置角度θn+1(t),具体为

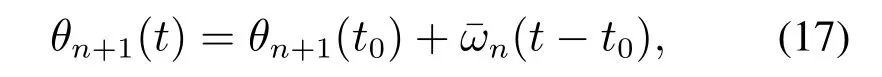
式中:θn+1(t)为电机转子在第(n+1)个区间任意时刻t的位置角度;θn+1(t0)为电机转子在第(n+1)个区间起始时刻t0的位置角度.

对于一个区间的起始位置角度,即该区间起始位置特征点对应的位置角度,如取线电感正值交点作为特征点,并以三相6/4规格开关磁阻电机为例,其确定方法如下:

由式(10)和式(11)可得线电感LBC与LCA的交点X2的位置角度θx2,满足如下关系式:

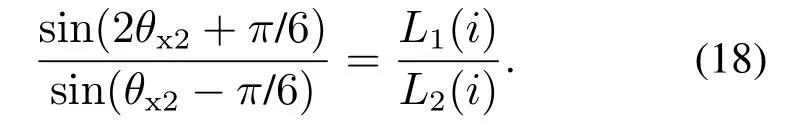
同理可得:线电感LAB与LCA的交点X4的位置角度θx4、以及线电感LAB与LBC的交点X6的位置角度θx6,分别满足如下关系式:

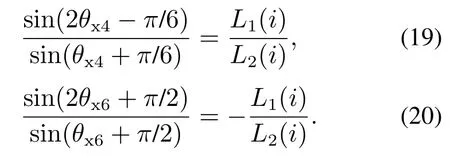
如取电机额定功率为4 kW、额定电流为16 A、临界饱和电流为9 A,并任取电机相电流分别为8 A、10 A以及16 A,根据式(18)–(20)可得其线电感各交点的位置角度如表1所示.可见,随着电机磁路饱和程度的增加,各线电感交点也即特征点的位置角度值会相应减小.

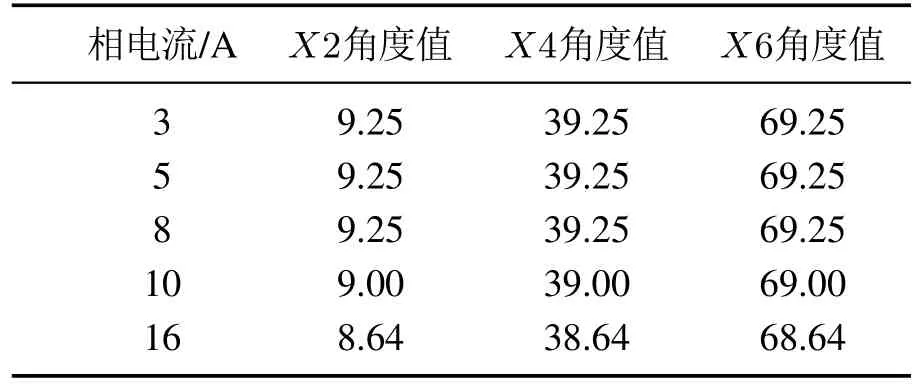
表1 线电感正值交点的位置角度Table 1 Position angle of positive intersection point of line inductance

至于各线电感交点的确定,可以根据表2所示逻辑关系进行判断,如当LAB与LBC相等且大于零时,可判断出此时线电感交点为X6,其他两个线电感交点X2和X4可依表2中所示关系进行确定.在确定好一个区间的起始位置角度后,即可根据式(17)计算出该区间内任意时刻电机转子的位置角度.

表2 线电感正值交点的逻辑关系Table 2 Logical relation of positive intersection points of line inductance

6 仿真研究

为验证上述理论分析的正确性,采用MATLAB/Simulink构建三相6/4结构开关磁阻电机仿真模型.仿真参数设置如下:电机功率取4 kW,临界饱和电流为9 A,电流斩波频率为20 kHz,非导通相脉冲注入频率为20 kH,占空比为15%.为说明电机在磁路非饱和及饱和两种情况下采用基于线电感特征点估算转子位置角度方法的效果,分别针对上述两种情况进行仿真研究.

6.1 电机磁路非饱和状态下的仿真研究

在临界饱和电流9 A之下,任取电机导通相电流为8 A,同时为验证电机在不同转速条件下采用基于线电感特征点估算转子位置角度方法的效果,分别任取500 r/min和1200 r/min两种转速进行仿真分析,得到相应的仿真波形分别如图6和图7所示,仿真结果见表3.从图6和图7可见,在磁路非饱和及两种不同转速条件下,其相电感和线电感曲线均为基本规则的正弦波,电机转子位置角度的估算波形与其实际波形均基本吻合:另外从表3可见,在两种不同转速下其转子位置的估算角度与其实际角度间的最大偏差分别为0.8◦和1.5◦.

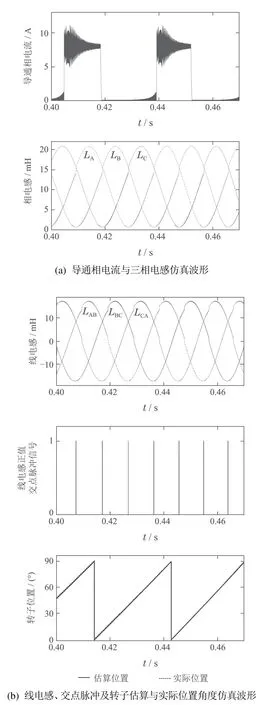
图6 电机转速为500 r/min时的仿真波形Fig.6 Simulation waveforms of speed at 500 r/min

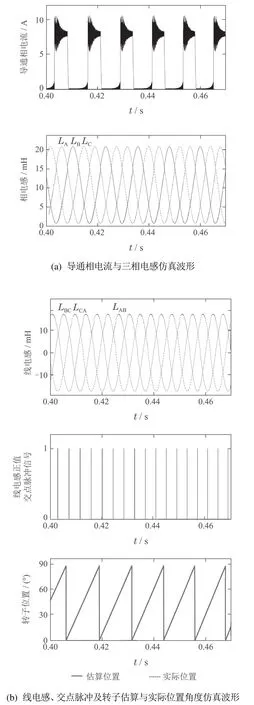
图7 电机转速为1200 r/min时的仿真波形Fig.7 Simulation waveforms of speed at 1200 r/min

表3 不同转速条件下的位置角度估算误差Table 3 The angle error with different speed

6.2 电机磁路非饱和状态下的仿真研究

在临界饱和电流9 A之上,分别任取导通相饱和电流分别为10 A和16 A,电机转速取600 r/min,得到相应的仿真波形分别如图8和图9所示,仿真结果见表4.从图8和图9可见,在电机导通相电流大于其临界饱和电流后,其相电感和线电感曲线均发生了变形,并且随着相电流的增大,其变形更为严重,但对应于线电感正值交点的脉冲信号之间的间隔却依旧保持不变,电机转子位置角度的估算波形与其实际波形也均基本保持吻合.另外从表4可见,对应于两种不同饱和相电流下的转子位置估算角度与其实际角度间的最大偏差均控制在0.9◦.

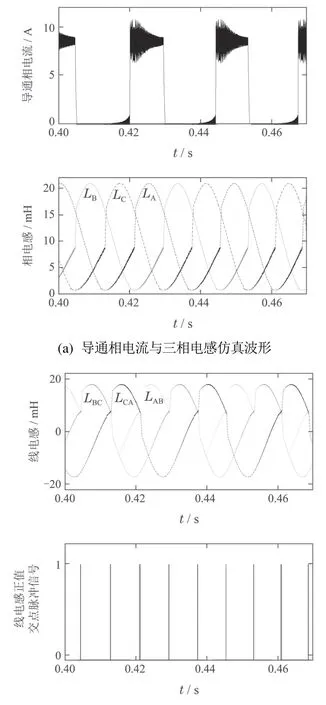
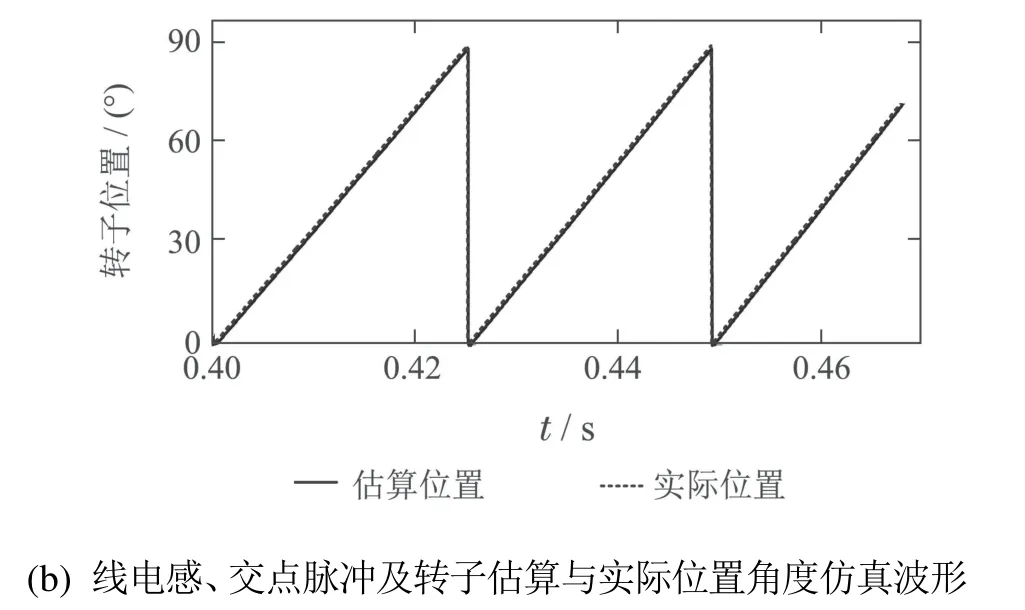
图8 电流取10 A时的仿真波形图Fig.8 Simulation waveforms of current taking 10 A

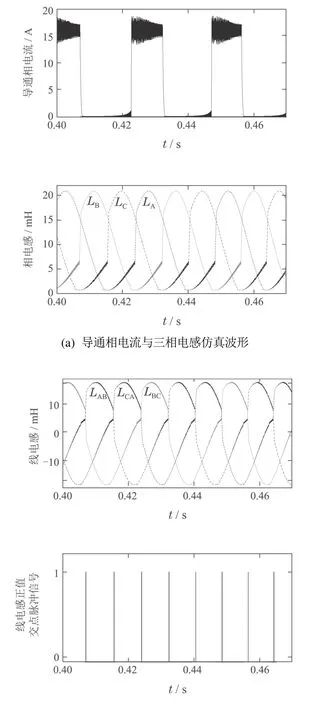
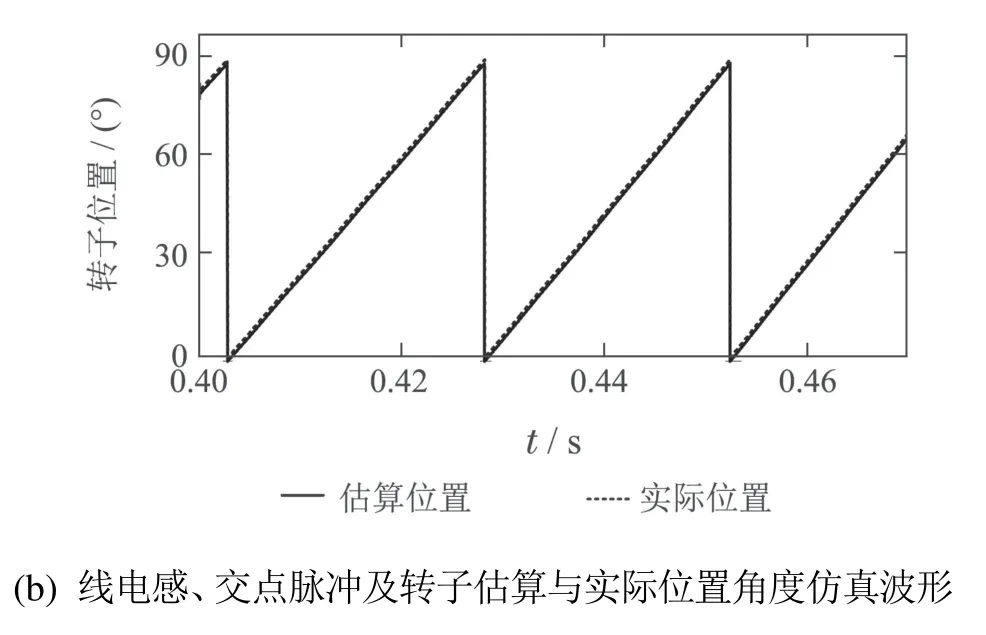
图9 电流取16 A时的仿真波形图Fig.9 Simulation waveforms of current taking 16 A

表4 磁路饱和条件下的位置角度估算误差Table 4 The angle error with saturation of magnetic circuit

7 实验验证

为进一步验证本文所提电机转子位置估算方法的可行性,以TMS320F28335 DSP为系统控制核心研制了一套实验装置,如图10所示.该实验装置包括一台4 kW三相6/4结构开关磁阻电机、控制器、制动器、扭矩传感器等,其中电机的主要技术参数如表5所示.为了与仿真结果进行对比分析,实验中相关参数设置与仿真时一致.同样,为说明该方法在磁路非饱和及饱和两种状态下的效果,实验分磁路非饱和与饱和两种情况分别进行,相关实验情况介绍如下.

图10 实验系统实物图Fig.10 Hardware of the experimental system

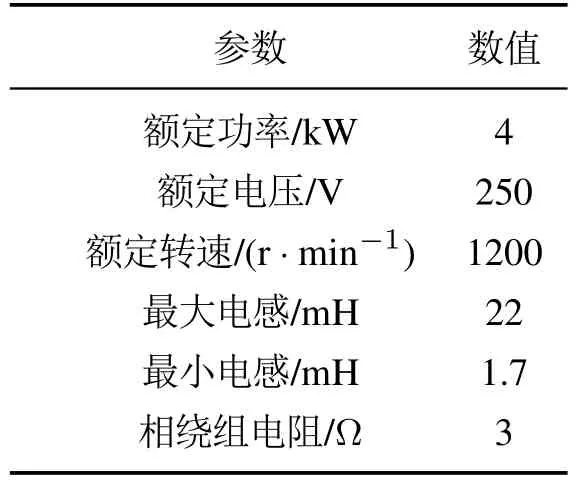
表5 三相6/4结构SRM主要技术参数Table 5 Main technical parameters of three-phase 6/4 SRM

7.1 电机磁路非饱和状态下的实验研究

在临界饱和电流9 A 之下,取电机导通相电流为8 A,同时为验证电机在不同转速条件下该无位置传感器控制方法的效果,分别取500 r/min和1200 r/min两种转速进行实验,得到相应的实验波形分别如图11和图12所示,实验结果见表6.从图11和图12可见,在磁路非饱和状态下,对应两种不同转速的线电感曲线均接近正弦波,转子位置角度估算波形与其实际波形均基本保持一致:另外从表6可见,两种不同转速下转子位置的估算角度与其实际角度间的最大偏差分别为1.0◦和1.8◦.

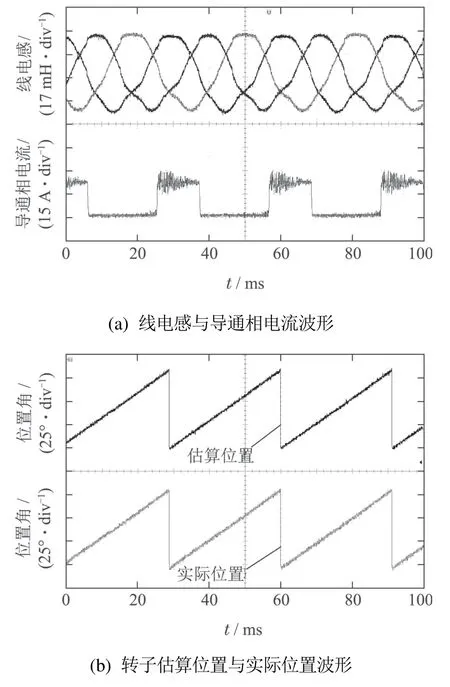
图11 电机转速为500 r/min时的实验波形Fig.11 Experimental waveforms of speed at 500 r/min

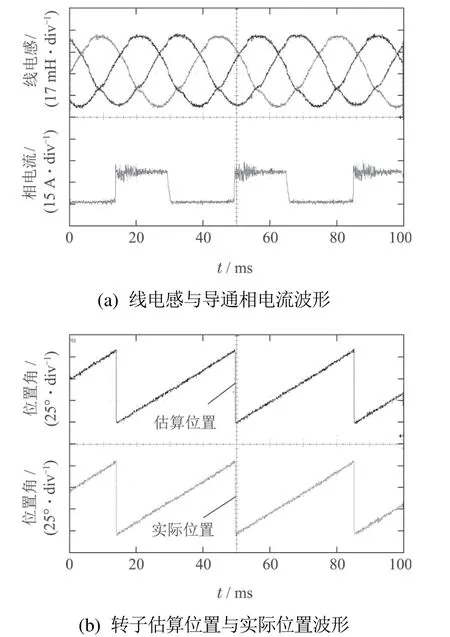
图12 电机转速为1200 r/min时的实验波形Fig.12 Experimental waveforms of speed at 1200 r/min

表6 不同转速条件下的位置角度估算误差Table 6 The angle error with different speed

7.2 电机磁路饱和状态下的实验研究

在大于临界饱和电流9 A的情况下,分别取相电流为10 A和16 A,并取电机转速为600 r/min 开展实验研究,得到相应的实验波形分别如图13和图14所示,相关实验结果见表7.可见,在磁路饱和状态下,相电感曲线发生了变形,从而导致线电感曲线也同样发生变形,且随着相电流的增大,其变形更为严重明显;但此时转子位置角度估算波形与其实际波形均基本保持一致,另外从表7可见,两种饱和电流下电机转子位置角度估算精度均控制在1.0◦.

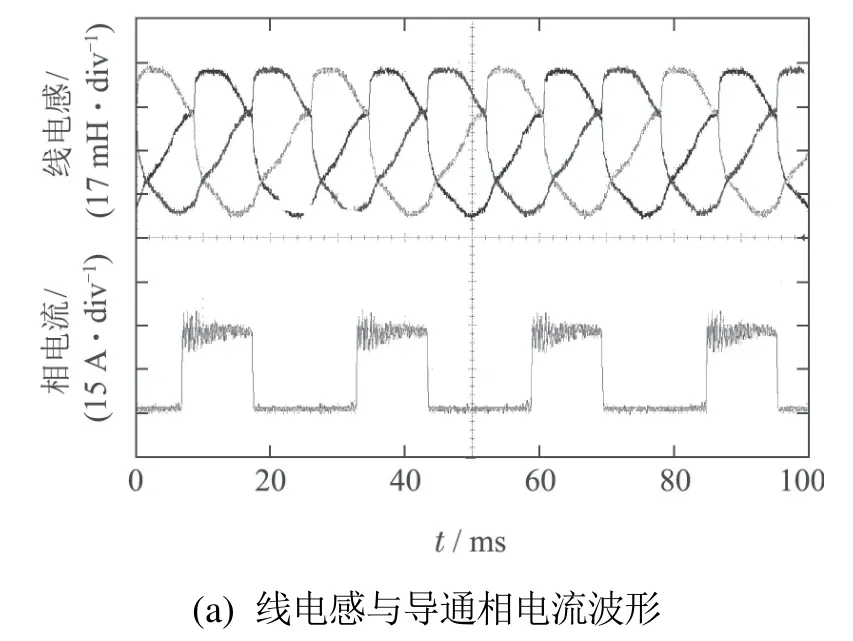
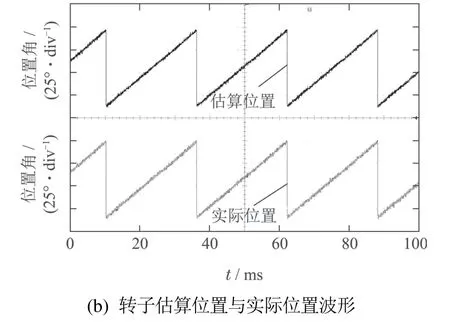
图13 电机相电流为10 A时的实验波形Fig.13 Experimental waveforms of current taking 10 A

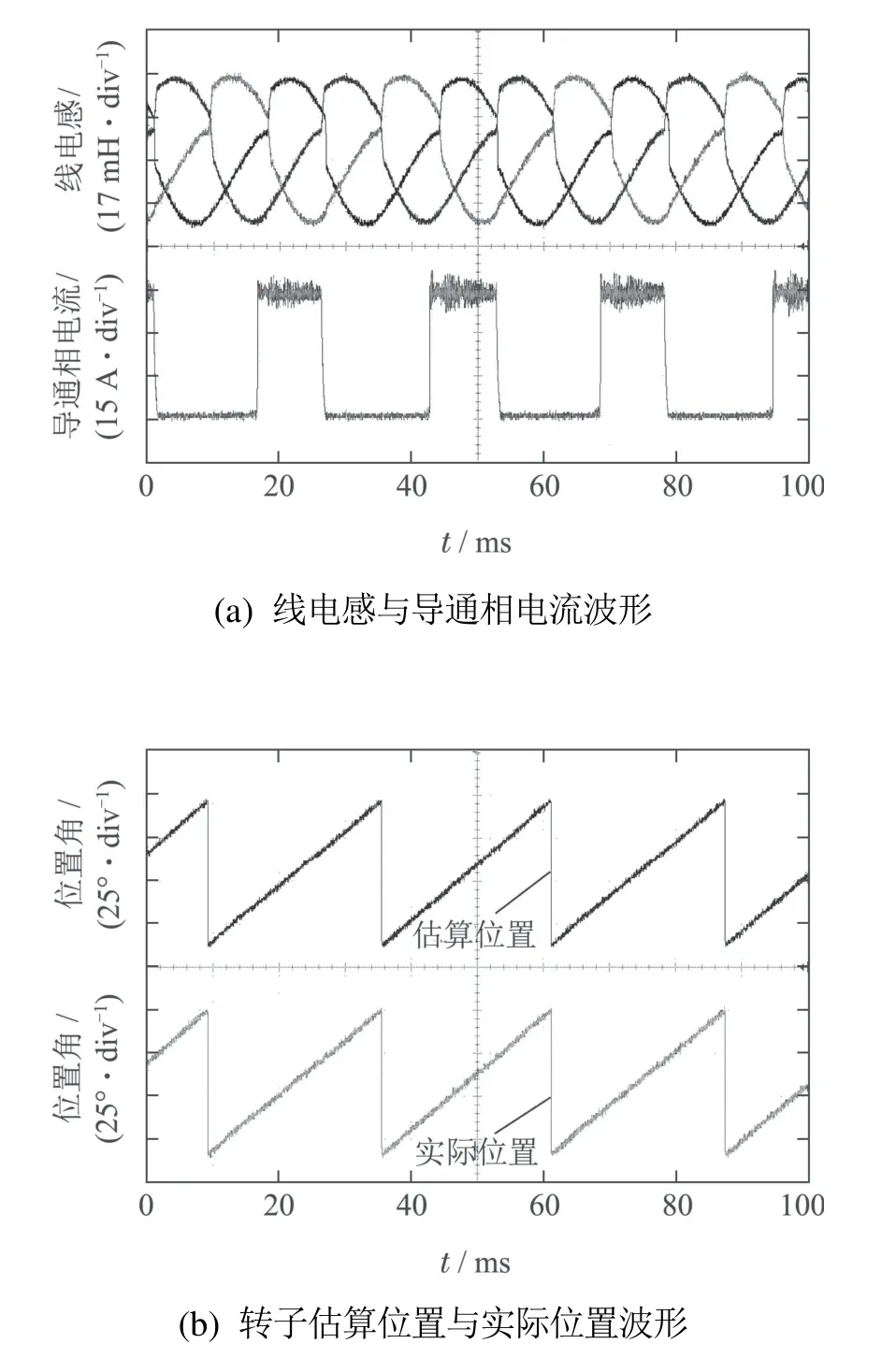
图14 电机相电流为16 A时的实验波形Fig.14 Experimental waveforms of current taking 16 A

表7 磁路饱和条件下的位置角度估算误差Table 7 The angle error with saturation of magnetic circuit

8 仿真与实验结果分析

根据上述仿真与实验结果,可得如下结论:

1)在磁路非饱和状态下,随着电机转速的提高,转子位置角度估算精度会有所下降.其原因在于随着电机转速的提高,单位时间内注入电机绕组的脉冲数将减少,从而导致所获得的相电感精度降低,并进而使相应的线电感交点位置角度误差增大,最终导致转子位置角度估算精度下降.

2)在电机磁路饱和状态下,相电感和线电感曲线均发生了变形,且随着相电流的增大,变形更加严重:但转子位置角度估算值与其实际值间的误差基本保持不变,说明磁路饱和对转子位置角度的估算精度没有影响,从而进一步证明了本文所提出的转子位置估算方法的有效性.

9 结论

针对目前开关磁阻电机在无位置传感控制方面存在受磁路饱和影响而导致转子位置估算精度不高的问题,提出一种线电感特征点定位的开关磁阻电机无位置传感器控制方法.给出了线电感及其特征点的基本概念,阐述了基于线电感特征点确定开关磁阻电机转子位置角度的具体实现方法,并通过仿真和实验对该方法的正确性进行了验证,结果证明了该方法的有效性和可行性,这对于提高开关磁阻电机无位置传感器的控制精度将具有重要意义.