借疑促思，让数学学习真实有效

韩向红

【摘  要】  教师进行教学活动时，必须要更新教学理念，引领学生参与到学习过程中去，从而让学生形成对问题的深入思考，形成自己个性化的认知，让学生的思维能力形成“看得见”的生长。本文提出要依托新旧链接，在迁移设置中激发疑问;尊重个性认知，在深入探究中解决疑问;强化本源思考，在积极反思中升级疑问;修缮思维路径，在拓展延伸中重生疑问，从而让数学学习真正发生。

【关键词】  迁移设置;深入探究;广泛反思;拓展延伸

2011年版《数学课程标准》对数学课程的理念进行了必要性的修缮，提出人人都要获得良好的数学教育，让不同的人在数学学习中得到不同的发展。这就需要教师进行教学活动时，必须要更新教学理念，引领学生参与到学习过程中去，从而让学生形成对问题的深入思考，形成自己个性化的认知，让学生的思维能力形成“看得见”的生长。

一、依托新旧链接，在迁移设置中激发疑问

兴趣是最好的老师，而激发学生内在兴趣的最好方法，就是让学生在学习之前就形成自己的疑惑，借助内在的疑问引发学生积极而主动地深入思考。在学生数学学习之前，这种疑问设置是促进学生内在动力发展的有效途径。学生接受数学知识的过程中，在新旧知识的链接上，教师可以提出具有启发性和思考性的问题，让学生在学习中意识到新知不新、新知不难，好像似曾相识但又相对陌生的感觉。因此，教师需要充分调动学生原先的知识储备，开掘出新授知识的支撑点，激发学生探究新知识的内在欲望。

如在教学“异分母相加减”时，教师在研讀教材中认识到这一部分教学的重点就在于引领学生借助通分将原本异分母的分数转化为同分母的分数。同时，这对于学生来说也是学习的一个难点。在教学中，教师则将这一部分的内容与学生之前学习过的知识进行深入统整，引领学生进行思考：我们在三年级时，已经学习了同分母分数的加减法，在分母相同的情况下，直接将分子相加减即可。如果相加减的两个分数的分母是不相同的，他们的分母和分子也可以直接相加吗？教师则引领学生利用最简单的1/2+1/3的算式以及结构图进行验证，发现这个算式最终形成的结果并不是想象中的2/5。面对这样的疑惑，教师则引领学生思考：是否可以将这一内容转化为我们已经学习过的知识进行计算呢？很多学生很快想到了通分。

在以上教学中，教师利用新旧知识的认知冲突，将学生的疑惑设置在学习之前，一方面激发了学生的认知兴趣，也历练了学生面对困惑、解决困惑的能力。

二、尊重个性认知，在深入探究中解决疑问

学生内在的认知困惑一旦形成，就会自然地关注知识经验和生活经验，并进行相应的联想、猜测和推理等思维活动。而在这样的过程中，教师就应该为学生搭建自主学习、探索新知和独立解疑的平台，让学生拥有自主性独立思考的空间，获得数学认知经验的积累，形成符合自己知识储备的个性化思考。

如在教学三下“解决问题的策略”时，教师就依托学生的生活经验创设了这样的情境：商场里一套运动服有130元和148元不等，帽子有16元和24元不等，运动鞋有85元和108元不等。小明拿着300元要购置一套运动服和一双运动鞋，最多可以剩下多少元？由于题目中给出的信息只有相关物品的单价，如果单从已知条件入手，就会缺乏相应的思维方法，彼此组合的类型也众多。教师则引领学生从最后所求的问题入手“最多剩下”，为学生顺势而上、顺藤摸瓜地尝试自主性解决问题明确了思考的方向。学生在深入探究的过程中，形成了以下解决问题的方法：其一，300-（148+108）=44（元）;其二，300-（130+85）=85（元）;其三，300-（130+85+16）=69（元）。

在这些方法中，虽然学生存在着一些认知上的偏差，对所求问题中的“最多剩下”以及“运动服和运动鞋”所包含的范畴理解上有一定的分歧，但在一定程度上却体现了学生内在的思维成果。而这就需要教师尊重学生内在的个体差异，要给予充分的机会让每个学生都能毫无保留地表达自己的认知意见，分享自己的思维过程。在充分尊重学生内在认知的基础上，教师就可以引领学生深入研究“在这样的问题中，为什么需要挑选最便宜的购买”以及“剩下的钱怎么求”等核心问题，并要求学生自己列出算式，并理解每一步都表示了怎样的价值和意义，从而为后续的对话交流建构起鲜明的思维路径。

三、强化本源思考，在积极反思中升级疑问

反思能力是生命个体思维能力生长的重要方式，教师要引领学生对数学知识进行深度反思，提炼出基于本源性问题的思考历程，引领学生逐步强化对数学新授知识的理解，促进学生内在认知结构的更新，让学生在分析和解决问题的过程中进行深度思考，完善学生内在的认知模型，促进学生核心能力的生长。

如在教学“两位数乘两位数”时，教师在练习时出示了两种完全不一样的竖式计算方法（如图），如果学生的内在认知仅仅就是要关注判断计算过程的对错，那就失去了其应有的探究价值。教师需要在展现学生认知错误的基础上，引领学生探究其中存在的错误，并对错误的成因进行洞察：观察这两个算式，是什么原因导致了这种错误？只有借助这种深入到算式内核中的问题，才能真正激发学生内在的认知欲望，学生的数学思考能力才能得到最大程度的释放：算式中21的位置写错了，这样的写法所表示的应该是21个1;21和13十位数上的1相乘，得到210，本身就应该表示21个10。

在逼迫式追问的过程中，学生的思维不断地向乘法笔算的内涵逼近。而对于第二个算式，教师也不能仅仅告知学生机械的计算方法，而是要让学生在运用方法解决问题的过程中进行反思。在错误性的资源中，教师着力引领学生理解了“21”的意义，通过移位和相加，0在计算过程中的省略就得到了自然的呈现。在这样的方法中，学生通过对本源性问题的思考，在反思中理解了知识的本质，不仅获取了笔算的基本方法，也建构起清晰的知识结构，并能正确运用笔算的方法感知乘法竖式计算所隐藏的本真要义，真正促进了学生内在认知能力的提升。

四、修缮思维路径，在拓展延伸中重生疑问

知识的建构并不是一蹴而就的，需要一个完整而漫长的体验和理解的过程。数学认知活动的最终目标是要引领学生从未知走向已知，再从已知向未知领域迈进，从而在学生的思维路径中提炼出全新的问题，真正走向更为广阔的思维空间，借以历练学生逻辑思维能力和创新意识。教学中，教师可以借助课堂内外的有机整合，将教材中所学习的内容拓展并延伸到课外，形成自己个性化的认知理解，建构起全新而完整的数学知识内在脉络。

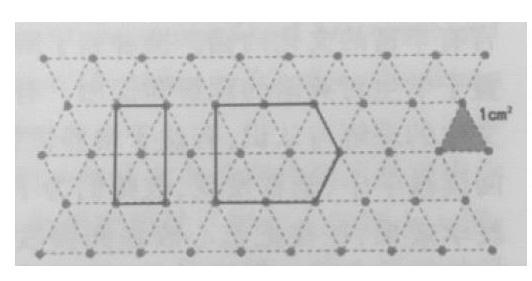
如在教学“钉子板上的多边形”这一部分时，教师引领学生对自己学习的过程和收获进行整合，尤其是要探索规律的核心内容、学习方法以及情感体验等方面进行深入感知。此时，教师则顺势抛出了相关的问题：这里有一个相对特殊的钉子板（如图），这是由一个个小三角形组成的。如果在这样的钉子板上围成多边形，还有规律吗？如此设置的疑问，就决定了学生决不能仅仅停留在自己已经掌握的知识信息中，而要让学生能够主动对自己内在的思维过程和形成的思维成果进行必要的反思、提炼以及运用，让学生带着对原有知识的认知和积累，参与到新问题的研究和解析过程中，进而能够形成全新的解决策略、认知方法和思想观点。

总之，有了疑惑，才会有思考，可以说“疑惑”是开启学生内在认知动力的重要方法。因此，数学教学就应该引领学生通过设置疑问，让学生学会思考;通过解决疑惑，让学生学会探究;通过消释疑问，让学生学会反思;通过重新生发疑问，让学生学会拓展。正是在这样循环往复的过程中，学生的数学学习才会捕获鲜明可感的资源，学生内在思维的生长才会拥有广阔的认知空间，让儿童感受到内在的学习价值，形成了丰富的认知意义。只有这样，数学学习才能真实发生。