立足生活常识 导向核心素养

杨亚军

【摘 要】 近两年，高考试题已清晰地从围绕知识、能力的命题向素养立意下的围绕育人目标的命题进行转变。如何在课堂教学及日常训练中落实，这是一个全新的课题。本文立足生活常识，从设计编制培养和发展学生核心素养的“问题”这个角度做了一点探索与实践。

【关键词】 核心素养  数学抽象  几何模型

新课程标准从政策层面、高考从评价选拔层面都要求教育要指向学生的核心素养，要注意发展学生的高阶思维能力。这就要求我们要尽快从过去的一味训练学生“解题”，转向启发、指导学生学会“解决问题”。要做好这个转变，对我们教师而言，很重要的一点就是要学会立足生活、立足学生实际，给学生设计或编制有价值的“问题”。

“山路弯弯”，不论是“千峰叠翠万重烟，清风索绕十二盘”的青海十二盘坡，还是318线上的怒江七十二道拐，这些盘山公路之所以有这么多弯、这么多拐，这其中是有科学道理的。下面，我就立足这一生活中的现象和常识，在学生学习了空间角的计算之后，给学生提出这样一个对学生而言既熟悉又陌生的“问题”——同学们试着应用我们所拥有的知识与方法，重点从数学的角度，给出“在陡峭的山坡上修公路，为何都修成了盘山公路”的道理之所在（记为“探索性问题”）。

学生几乎都能说出修成盘山公路，路就不太陡，车就容易上去。还有学生可能会从机动车爬坡的安全性与能力，甚至有学生可能从道路交通设计等方面，搜索到修路时对路面所在斜坡坡度（或坡比）最大值的政策规定（如不同车速的公路，车速由高到低其道路的最大坡度从3%到10%，积雪寒冷地区的最大坡度推荐值不大于6%）。

在此基础上，引导学生挖掘此问题的本质原因：为什么修成盘山路后路面的坡度就能变小？在实际施工中，如何根据坡度的限定值，规划路线呢？（初步“具体化了的问题”）。教师适时、恰当地引导、启发学生，设法把这个问题理想化、数学化、模型化。路要修在山坡上，山坡很陡峭。从数学的角度，这里涉及到数学中的什么角呢？——二面角——水平面与山坡的坡面所成的二面角。若咱们再把山路截取一个片段，山路在我们的眼中就不是弯的，而是直的了。自然地，学生会想到，把山路的坡角看成直线与水平面所成的线面角。至此，这个“具体化了的问题”通过理想化，与学生熟悉的立体几何中的二面角、线面角建立了联系。这时，刚才的“问题”可以进一步数学化，成为一道“具体的数学题”——已知二面角的大小，在其中一个半平面内确定一条与二面角的棱相交的直线，使得该直线与另一个半平面所成的角为给定的值。

至此，实现了把“实际问题”数学化，这一过程中有分析判断，有数学抽象。

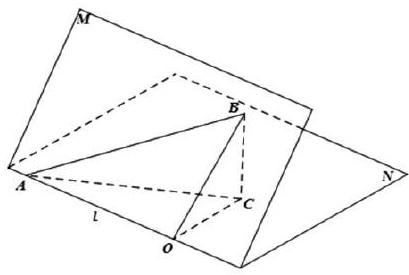
接下来，对大多数学生而言，应该是轻车熟路了。在立体几何中，我們有研究解决这种二面角与线面角的几何模型。如图，在二面角M-l-N中，用半平面M代表山坡的一段坡面，用半平面N代表水平面，AB代表山路的一个片段。在图中作BC⊥平面N于点C，作CO⊥l于点O，连结BO，则BO⊥l. 从而∠BOC是二面角M-l-N的平面角，∠BOC的大小就表示该段山坡的陡峭程度.而∠BAC是直线AB与平面N所成的线面角，其大小就表示这段山路的坡角大小。

显然∠BAC<∠BOC（∵BA>BO），这就是为什么要修盘山路的数学解释。

事实上，这里用到了立体几何中一个很重要的模型：四个面都是直角三角形的四面体（三棱锥）。这个模型可以帮助解释“直线与它在平面内的射影所成的角是该直线与平面内所有直线所成的角中最小的”（∵cos∠BAO=cos∠BAC·cos∠OAC，这就是特殊三面角公式，它给出了线面角定义的合理性和科学性：为什么把一条直线与它在平面内的射影所成的角定义为该直线与该平面所成的角——该角的最小性、唯一性）。这一过程中有模型，有推理，也有计算。

教师亦可在这儿提一下一般三面角公式，提醒有兴趣的同学下去研究或查阅有关资料，了解其具体表达式及含义。

上面的模型（图中的四面体BAOC）也是研究正棱锥的“标本”，它包含了正棱锥几乎所有的基本量及其关系。视点B为正棱锥的顶点，则点C为正棱锥底面正多边形的中心，从而BA为正棱锥的侧棱，BO为正棱锥的斜高，AO为正棱锥底面正多边形一条边长的一半。

通过这样的“问题解决”，学生不仅能深刻理解线面角与二面角的概念及其计算，还能应用所学数学知识，研究解释生活中现象。在此过程中，学生对数学的应用价值也有了更深入地认识，同时也较好地发展了学生的数学核心素养（数学抽象、数学推理、数学建模、数学计算等）。自然地，这也是训练、发展学生分析、评价、创造这些高阶思维的一个很好的素材。

参考文献

[1] 普通高中数学课程标准（2017年版）.中华人民共和国教育部制定.人民教育出版社，2018.1：4-8.

[2] 葛军.新编高中数学奥赛指导.南京师范大学出版社，2010.6：245-246.