基于粒子滤波的篮球旋转投射最优角度分析研究

冯 超

(大连财经学院，辽宁 大连 116600)

篮球运动是最为广泛的球类运动之一，篮球投篮是得分的关键，篮球旋转投射过程中，受到的臂力作用大小的差异性影响，导致篮球旋转投射的偏差难以控制，需要构建篮球旋转投射的篮球旋转投射的最优角度分析模型，采用轨迹跟踪控制方法，进行篮球旋转投射的角度解算，研究篮球旋转投射的角度分析方法，进行参数估计，建立篮球旋转投射的运动学模型，提高篮球旋转投射的精度。相关的篮球旋转投射最优角度分析方法研究受到人们的极大关注[1]。

当前，对篮球旋转投射的最优角度分析方法主要采用最大似然估计和最小二乘估计方法，结合参量优化估计，进行篮球旋转投射的角度计算[2]，但上述方法进行篮球旋转投射的角度计算的自适应性不好，容易受到扰动影响，对此，提出基于粒子滤波的篮球旋转投射最优角度分析计算方法。构建篮球旋转投射的动力学和运动学模型，构建篮球旋转投射最优角度的运动控制律，采用自适应的轨迹修正方法进行篮球旋转投射过程中的力学控制，实现篮球旋转投射最优角度分析。最后进行仿真实验分析，得出有效性结论。

1 篮球旋转投射的运动学模型及轨迹方程建模

1.1 篮球旋转投射的动力学和运动学模型

为了实现篮球旋转投射最优角度分析，构建篮球旋转投射的动力学和运动学模型，结合动态差分模型进行篮球旋转投射的轨迹参数分析和特征采样[3]，采用传感器进行篮球旋转投射的运动力学和飞行力学参数采集，对采集的篮球旋转投射参数进行动态寻优自适应融合，提取篮球旋转投射最优角度的相关约束参量模型，结合粒子滤波算法，进行篮球旋转投射的最优角度解算，整个算法的实现示意图如图1所示。

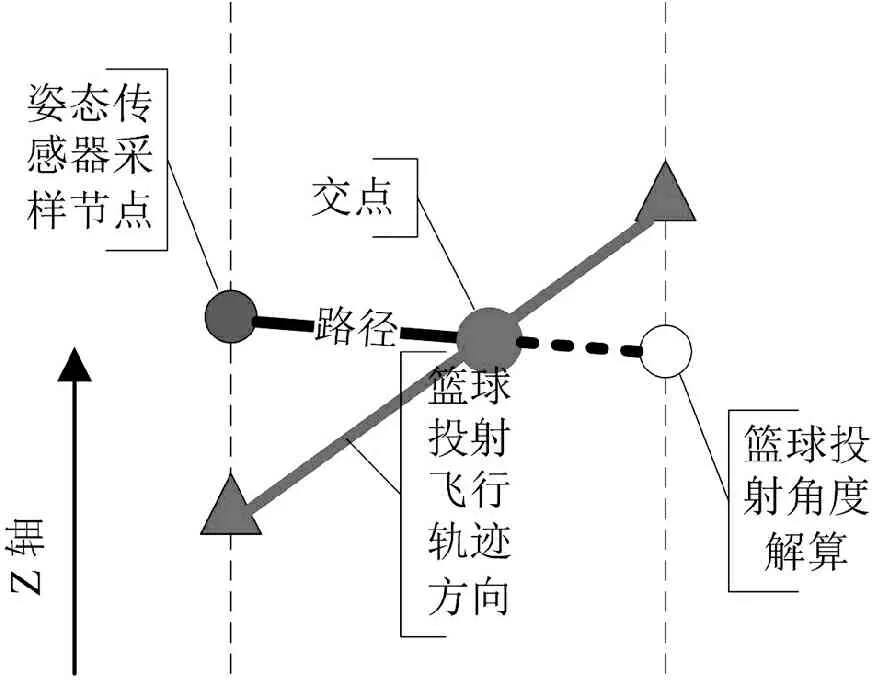
图1 篮球旋转投射的最优角度解算的实现示意图

根据图1所示的篮球旋转投射的最优角度解算示意图，采用局部动态寻优方法，进行篮球旋转投射的虚拟飞行空间分布式重构设计[4]，得到篮球旋转投射的被控对象稳定特征解为：

(1)

利用篮球旋转投射飞行轨迹跟踪控制方法进行参量估计和投射角度的计算，得到篮球旋转投射的飞行理想角度，构建运动学模型描述为：

(2)

采用时滞二自由度模拟方法，进行篮球旋转投射的参数融合和自适应跟踪识别，采用轨迹终点位置误差偏移纠正方法进行篮球旋转投射的角度纠偏，结合粒子群滤波，得到篮球旋转投射的运动学数学模型：

(3)

定义d(t)=d1(t)+d2(t)，在小扰动干扰下篮球旋转投射的角度计算过程为一个线性规划问题[5]，把篮球旋转投射的角度计算转换到一个线性反馈系统中，得到自适应学习权值为：

(4)

其中x(t)=x1(t)，x2(t)，…，xt(t)T是篮球旋转投射飞行轨迹的空间位置状态向量，d1(t)和d2(t)分别表示Kalman滤波的稳定解和时滞解，由此构建篮球旋转投射的飞行动力学和运动学模型，结合动态差分模型进行篮球旋转投射的基元轨迹方程建模，提高篮球旋转投射最优角度计算和自动分析能力[6]。

1.2 篮球旋转投射的基元轨迹方程建模

构建篮球旋转投射的动态运动基元线性控制矩阵，篮球旋转投射动态运动基元的学习轨迹为：

(5)

(6)

将篮球旋转投射轨迹采用分段式轨迹学习方法进行自动跟踪识别，采用分段线性拟合的方法，构建篮球旋转投射的最优角度计算模型[7]，采用决策树信息融合方法进行篮球旋转投射最优角度标定，学习轨迹的寻优过程描述为：

(7)

式中AT表示矩阵A的转置，篮球旋转投射的基元函数记为：

(8)

(9)

构建最小二乘规划模型进行篮球旋转投射的轨迹跟踪识别，在高维相空间中实现篮球旋转投射最优角度分析，得到篮球旋转投射轨迹的发力位置误差修正矩阵描述如下：

(10)

p=-(fx1+gx2)Pi，i=1，2，3，4

(11)

q=detAPi，i=1，2，3，4

(12)

根据上述分析，采用误差偏移纠正方法进行篮球旋转投射的力学修正，对篮球旋转投射的最优轨迹进行模糊搜索[8]。

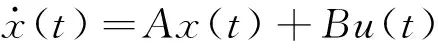
(13)

采用动态搜索方法，进行篮球旋转投射的基元轨迹跟踪，得到优化控制方程描述为：

(14)

最优角度计算的稳定性充分条件为：

(15)

(16)

上式将篮球旋转投射的最优角度计算问题转换为轨迹泛化过程，结合参量自动估计方法，进行篮球旋转投射的最优角度分析。

2 篮球旋转投射最优角度分析优化

2.1 篮球旋转投射最优角度寻优控制

本文提出基于粒子滤波的篮球旋转投射最优角度分析计算方法，采用最大似然估计方法进行篮球旋转投射最优角度的优化计算，进行篮球旋转投射的基元轨迹方程建模，结合双曲微分方程得到篮球旋转投射的动力学方程描述为：

(17)

其中u：I×IRd→IR是实值函数，d≥4。进行篮球旋转投射的自适应跟踪，当投射角度满足：

Ψ(h1，h2)=Ψ+h1KZ1+Z2+Z3-1KT

+h2MZ2+Z3-1MT<0

(18)

在同一平面的相邻平面内，构建篮球旋转投射的动力学模型，收敛参数满足约束条件：

Ψ(h1，0)=Ψ+h1KZ1+Z2+Z3-1KT

+h2LZ2+Z3-1LT<0

(19)

在篮球旋转投射的稳定状态下，采用模糊二自由度跟踪方法[9]，得到篮球旋转投射的最优角度分解模型满足：

(20)

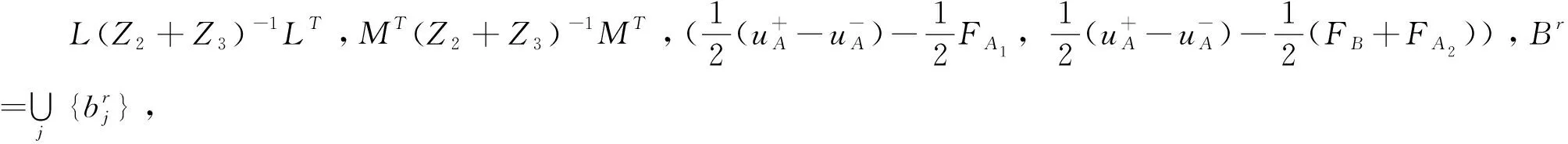
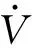
[F(X，t)+D(t)+K]

(21)

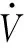
(22)

结合Lyapunov稳定性原理，得到进行篮球旋转投射最优角度计算和收敛性控制。

2.2 粒子滤波优化

在解算过程中结合粒子群滤波进行篮球旋转投射最优角度的自适应寻优控制，篮球旋转投射最优角度计算的粒子滤波模型描述为：

(23)

(24)

(25)

(26)

(27)

其中：

(28)

综上分析，实现了对篮球旋转投射最优角度标定，采用自适应的轨迹修正方法进行篮球旋转投射过程中的力学控制，实现篮球旋转投射最优角度分析，输出为：

(29)

(30)

(31)

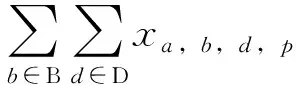
(32)

综上分析，实现篮球旋转投射最优角度分析计算，提高了篮球投篮的准确性。

3 仿真实验与结果分析

为了验证本文方法在实现篮球旋转投射最优角度分析中的性能，进行实验测试，采用Matlab进行仿真分析，初始化粒子个数为2000，寻优迭代次数为120，种群规模设置为20，状态参数设定为：

(33)

(34)

测试篮球旋转投射的投射角参数估计过程，得到测试结果如图2所示。

图2 篮球旋转投射的投射角参数估计结果

分析图2得知，采用本文方法进行篮球旋转投射最优角度分析，对参数的估计精度较高，测试篮球旋转投射的最优轨迹估计结果，如图3所示。

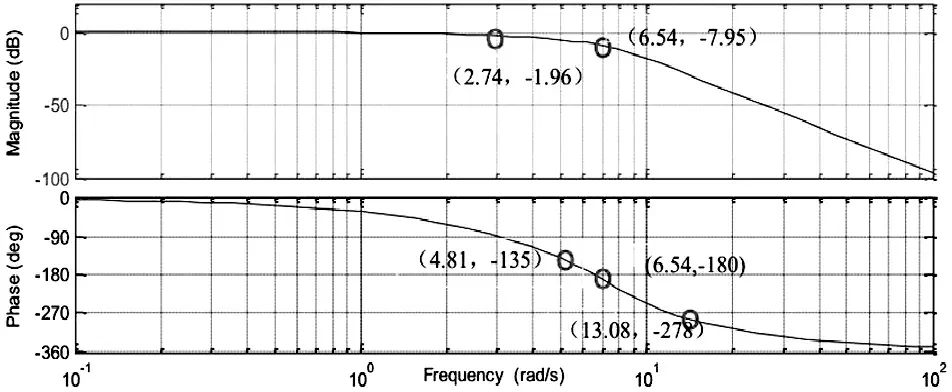
图3 篮球旋转投射最优轨迹估计结果

根据图3的轨迹分布，能准确实现篮球的旋转投射，提高投射的精度，测试不同方法进行篮球旋转投射的准确度，得到对比结果见表1，分析得知，本文方法进行篮球旋转投射最优角度分析，提高了投篮的准确率。

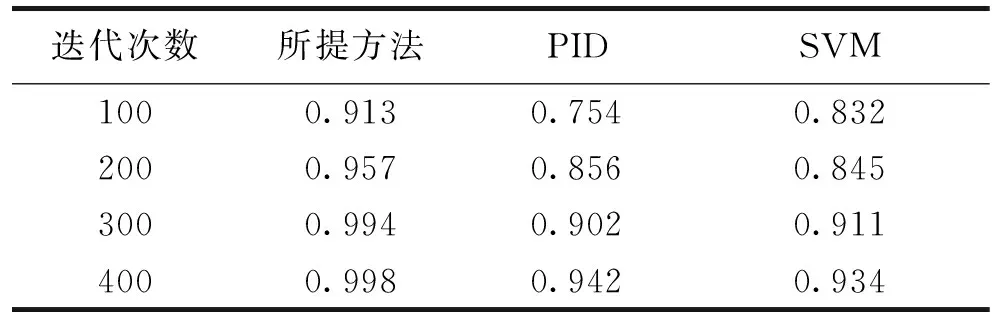
表1 投射准确性对比

4 结语

构建篮球旋转投射的动力学和运动学模型，结合动态差分模型进行篮球旋转投射的基元轨迹方程建模，采用最大似然估计方法进行篮球旋转投射最优角度的优化计算，在解算过程中结合粒子群滤波进行篮球旋转投射最优角度的自适应寻优控制，构建篮球旋转投射最优角度的运动控制律，采用自适应的轨迹修正方法进行篮球旋转投射过程中的力学控制，实现篮球旋转投射最优角度分析。分析表明，所提方法能有效实现篮球旋转投射的最优角度分析，提高投篮的准确性。