运动控制和自适应模糊控制在码垛机器人中的应用

刘 光 文 桦 梁 颖

(1.驻马店职业技术学院机电工程系，河南 驻马店 463000；2.黄淮学院信息工程学院，河南 驻马店 463000；3.中原工学院机电学院，河南 郑州 450007)

随着食品冷链技术的发展，人工码垛工作强度大、效率低、工作环境恶劣，对人体健康损害较大。而机器人码垛机具有灵活性强、处理速度快、有效载荷大等特点，可适用于食品冷链技术中的物料搬运。将机器人应用于生产线进行码垛，其难点多为应用程序的选择和放置。码垛机器人应用程序目标是通过生成一个代表其环境的计算机仿真模型及实际的机器人模型模拟机器人的4个关节(腰、肩、肘、腕)，并观察机器人末端执行器的位置，最终实现对机器人的行为控制[1-2]。在模型开发中，常使用机器人工作单元仿真模型开发和机器人仿真执行两种方法实现码垛机器人的应用程序。上述两种模型均以预定义的坐标、整体布局校验、机器人的输入输出、工作区域、碰撞和接近目标检测以及任务完成后的循环时间监控为基础进行输出。

作为一种运动学仿真工具，机器人仿真主要通过高精度的单元级校验方法，仿真一个或多个运动设备的运动状态发生变化的系统。还可为机器人应用程序提供一个“模拟”工作站，该工作站可以检查和评估各种参数，如循环时间、最佳路径、工作单元布局以及单元内的实体。文章拟提出一种基于计算机的机器人码垛系统模型生成方法，用于整个机器人应用系统的仿真监控和评估。重点模拟机器人的4个关节(腰、肩、肘、腕)，使用拉格朗日动力学来分析和估计运动模型，并建立运动的逆方程，使用自适应模糊控制算法设计一个新的控制器，并利用模糊控制和自适应控制算法的优点以编程方式控制该控制器，可有效地满足食品物料搬运的高速、重载要求，机构的动态性能得到大大改善。

1 机器人和机器人码垛系统

1.1 码垛系统

机器人码垛系统应用程序使用机器人在线进行码垛袋，并侧重于取放应用。机器人在取货点取包，然后将包放到托盘上，机器人模型为多关节四轴气动动力的码垛机器人(见图1)[3-5]。其连杆由一个封闭的平行四杆机构组成，并将两组小副四杆结构连接在一起，以满足腕部定位的要求，从而改善机器人的动态特性。

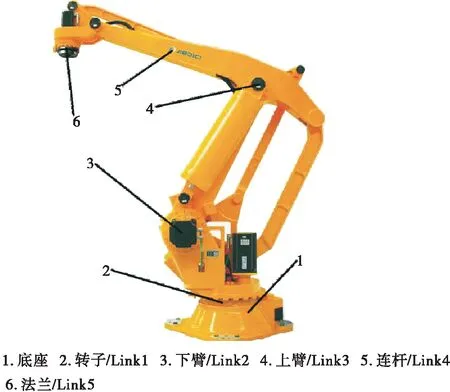
图1 码垛机器人的结构

码垛机器人在执行过程中循环周期最快可达1 600次/h，能处理高达140 kg的重量。其精度较高，可重复定位精度至1 mm[6]。常用的码垛机器人由底座、转子/Link1、下臂/Link2、上臂/Link3、连杆/Link4、法兰/Link5、电机D-axis等部件组成，基于本体的坐标系统进行定位，末端夹手坐标采用基于三轴(X,Y,Z)的坐标系统。

1.2 工作单元仿真模型

(1)创建零件模型：在三维建模软件中，采用实体建模来创建基本元素。

(2)建立设备模型：设备模型代表实际的工作单元组件，可分为机器人设备模型和非机器人设备模型两类。设备模型的建立以零件模型的基础定位为基础坐标系。码垛机器人的链接使用与其编号相关联的附件特性，每个附加的链接受父/子关系的约束。

(3)布局中定位装置型号：工作单元模型的布局以实际工作单元的环境为基础，使用机器人末端的夹爪坐标系统，模型和设备在环境中的放置基于实际工作单元的布局。

(4)在布局中定义设备的运动目标：设备模型的运动属性定义了设备模型的关节在零位、位置、速度和加速度方面的运动限制。每个连接都被认为是正在进行的链接中的一部分。码垛机器人的关节1是一个腰关节之间的联系基地和转子，关节2是一个肩关节，转子之间的联系，关节3是一个手肘传递到上臂的连接关节，关节4是腕关节与上臂连接杆之间的连接点，关节5是一个爪关节连接法兰的连接杆，每个关节都有各自的运动极限。

(5)设备行为和编程：设备运动是由一系列的几何点(GP)决定的，这些点为机器人创建了运动路径。GP和系列的定位是基于移动模式和布袋的安排，通过输入每个关节的值、输入X、Y和Z的绝对值以及单击鼠标创建GP。其中，获取准确位置最合适的方法是输入GP的X、Y、Z的绝对值，目前已确定了74个GPs。

2 码垛机器人的运动控制

码垛机器人的连杆通过一个大地坐标系移动或是与r-关节一起旋转，而第4个连杆之间会产生严重的耦合，通过大地坐标系移动的方法可以克服耦合现象，易于控制，但占用大量的工作空间，在货物的搬运和码垛方面灵活性较差[7-8]。经过大量的分析、计算和优化设计，码垛机器人可用于包装生产线上的货物搬运和码垛。该类型码垛机器人具有响应快、控制便捷、操作范围大、末端负荷大、安全可靠等特点。

2.1 正运动学计算

图2为码垛机器人空间几何图，利用几何法进行运动学正反解析。利用几何法建立的运动学更直观，比传统MDH方法更为简便。

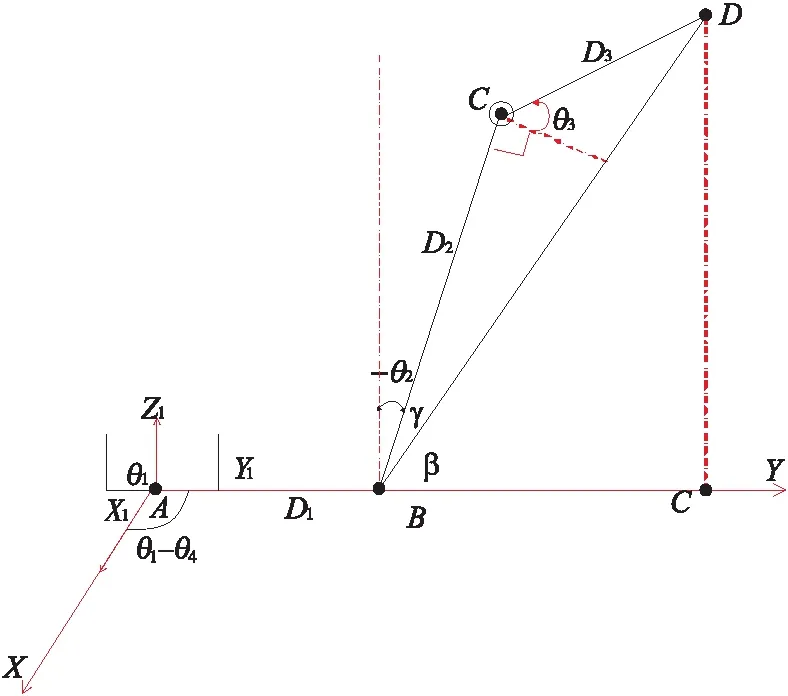
图2 码垛机器人空间几何图

连杆参数：关节轴为i，连杆转角为аi-1，连杆长度为Di，连杆偏距为di，关节角为θi。从图2中可以看出，机器人的姿态跟θ1、θ4有关。所以推导出机器人的姿态为：

(1)

机器人的位置跟θ2、θ3有关。所以推导出机器人的位置为：

(2)

根据姿态和位置可以得到码垛机器人运动学正解

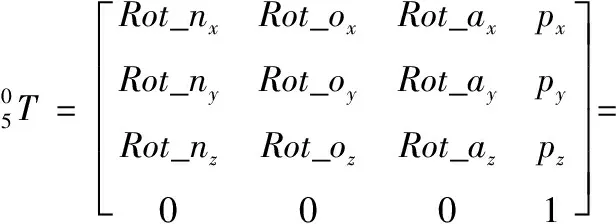
(3)

2.2 解析法反解运动

(1)第1个轴反解：当py≠0时，θ1=

或θ1=

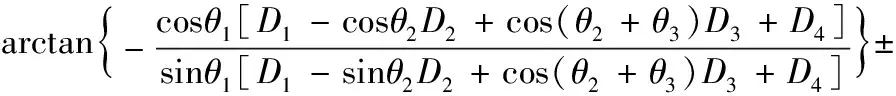
(4)

当py=0时，θ1=±900。

θ1是唯一解。

(2)第4个轴反解：

θ4=arctan2[sin(θ1-θ4),cos(θ1-θ4)]+θ1。

(5)

θ4是唯一解。

(3)第2个轴反解：

(6)

所以θ2是唯一解。

(4)第3个轴反解：-900≤θ3≤900。由余弦定理可知cθ1≠0。

c(θ3+900)=

(7)

θ3是唯一解。

2.3 码垛机模型的动力学分析

2.3.1 机器人的简化模型 码垛机的主要结构是封闭的平行四杆连杆，并连接两组小平行四杆连杆的结构。4个马达分别用于驱动手腕、水平滑块和垂直滑块的旋转和移动[9-11]。为了计算方便，可仅考虑其腰部和平行四连杆的连接年龄。如图3所示，将前臂AE、连杆AB、后臂CD及小臂DP的长度分别设为l2，l3，l5，l6；分别用l2c，l3c，l5c，l6c表示其质心和旋转轴之间的距离；BC的长度、连杆的质心与B点之间的长度、后臂的质心与其C点之间的长度、小臂的质心与E点之间的长度、终点P点设为l0，r3，r5，r6，rr6；DP表示垂直滑块与O1点之间的水平距离；θ1、θ2、θ3分别为腰部、前臂和小臂的旋转角度。

利用拉格朗日第二动力学求解公式(即系统的势能和动能之差)，分析机器人的动力学方程。

图3 MJR机器人的简化模型

2.3.2 系统的广义坐标 为了方便计算，可忽略机器人手腕的运动，因此，该系统可化简为3个自由度的三维模型。将两个滑块的位置坐标x1和y4转换为XOY中的角度变化θ2和θ3。因此，将θ1、θ2和θ3作为系统的广义协调。

2.3.3 机器人动力学模型 由于采用平行四连杆机构，连杆之间会产生很大的约束力[12]。因而，应首先导出系统的拉格朗日方程。假设坐标OXYZ中每个链接的向量半径为ri(i= 1,2，…,7)，系统的动能为：

(8)

式中：

I1、I2、I3、I4——连杆1、2、3、4的转动惯量;

Mi——关节的质量，i=1,2,…,4。

(9)

式中：

Pci——链接i的垂直坐标。

机器人的非保守力为关节转矩τ1，τ2，τ3和τ4，分别为腰部、水平滑块和垂直滑块的电机输出扭矩，机器人的非线性动力学方程可表示为矩阵形式：

(10)

3 自适应模糊PID控制

3.1 参数设置

自适应模糊PID控制器的推导过程是以自适应模糊规则表为基础进行的，PID的参数可在线调整，通过对预先保存的模糊控制规则表的查询可以改变参数[13]。传统的PID控制器可描述为：

(11)

式中：

P、I、D——自适应模糊PID控制器的比例增益、积分增益、导数增益参数；

Out(t)——控制器输出，(°)；

E(t)——误差信号，(°)。

为使被控对象达到良好的动静态性能，采用的PID控制器设计算法是以e和de(t)/dt等参数为基础，通过计算在线调整KP、KI和KD参数。

3.2 控制器设计过程

(1)输入和输出变量：ec、e为输入参数，而KP、KI和KD为输出参数。

(2)输入和输出变量的模糊语言：将输入变量e、ec的量子秩选择为13个秩，e、ec={-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}。上述参数模糊集全部定义为{NB，NS，ZO，PS，PB}，其中NB，NS，ZO，PS和PB分别为负大、负、小、正、小和正大；此外，选择KP，KI和KD的量子等级作为10个等级，KP，KI和KD={0,1,2,3,4,5,6,7,8,9}。每个变量的三角分布隶属函数如图4、5所示。参数e的量子因子Ke=10，量子因子Kec=100；KP，KI和KD的量子因子为KUP=3，KUI=0.7，KUD=0.5。

图4 e和ec的模糊隶属函数

图5 KP，KI和KD的模糊隶属函数

(3)PID参数调节：根据其模糊规则表进行调节，实际控制值是精确值和量子因子的乘积。

3.3 准确率

在数据集中分别按总量的1/4、1/3、1/2和3/4作为测试数据集，并按式(13)、(14)分别计算检测准确率和误报率。

(12)

式中：

A——准确分类数据；

B——测试数据集容量；

C——检测率，%。

(13)

式中：

M——误检为其他类型的数据；

K——测试数据集容量；

L——误报率，%。

4 仿真

为验证试验设计的控制器对堆垛机的有效性，利用Matlab软件对其进行仿真。由图6可知，当腰部输入角度为1 rad，上升时间为50 ms，调节时间为10 ms时，稳态误差为1.5%，说明自适应模糊PID控制在非线性系统响应方面比传统的PID控制更具优势，并且不存在过冲现象。因此，控制器可满足码垛机系统的性能要求。

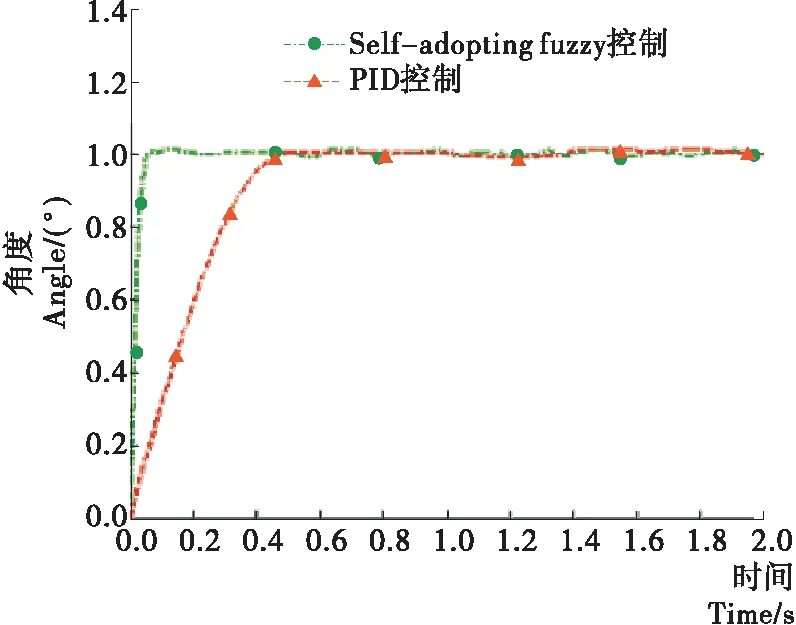
图6 传统PID控制器与自适应模糊PID控制器的比较

机器人负载的变化导致控制器需较强的鲁棒性。由图7可知，机器人在10 N·m余弦信号的干扰下仍可正常工作，因此控制器具有坚固的鲁棒性。

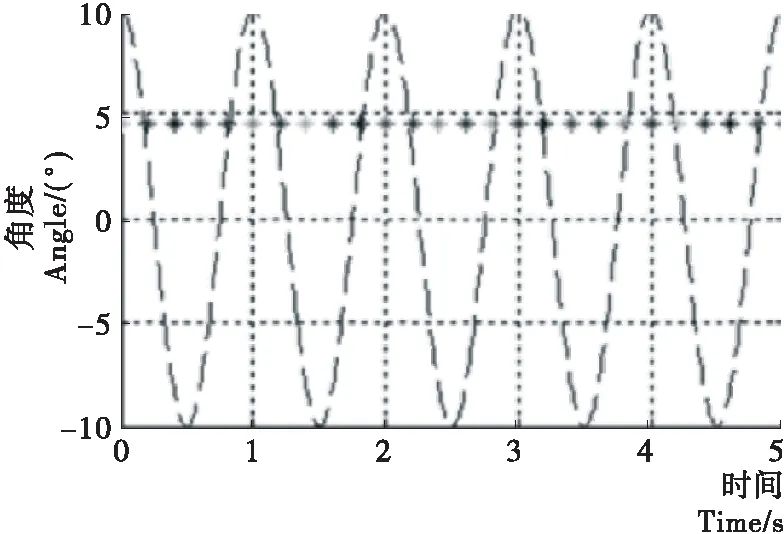
图7 带有干扰信号的系统的输出响应

5 结论

采用拉格朗日动力学方程分析了码垛机器人的动力学性能，建立了逆动力学模型。采用自适应模糊PID控制算法设计码垛机器人的控制器，相对于传统的PID控制算法更具优势，可在很大程度上消除对冲，具有较强的鲁棒性。试验设计的码垛机器人可有效地满足食品物料搬运的高速、重载要求，机构的动态性能得到大大改善。后续可研究控制收敛去速度。