考虑滑带强度参数分区取值的堆积层滑坡稳定性分析方法

闫玉平，肖世国

(西南交通大学地质工程系，四川 成都 610031)

0 引言

堆积层滑坡在我国西部地区广泛分布，基覆界面往往表现出应变软化特性，是潜在最危险滑面之一。滑面贯通经过由局部点的破坏再到整体失稳的过程，呈现渐进性破坏特点[1]，滑带强度参数存在不同区段有所不同的特征。对于此种滑坡，有学者在极限平衡法的基础上[2]，以滑带土变形为切入点，考虑其简化的应力应变关系，反推出滑面不同位置处强度参数，从而分析边坡稳定性[3-9]。然而，该方法计算模型较为理想，实际应用有所不便。卢应发等[10]基于对滑体关键块力学行为及力传递特征的分析，将滑体(含滑面)分区划分条块，以此分析坡体稳定性。极限平衡法实际操作简单，但无法考虑坡体变形，数值模拟法可反映坡体变形[11-12]，因而有学者曾基于土体应变软化本构模型采用此法对简单边坡稳定性进行分析[13-18]。但是，应变软化本构模型的建立依赖于试验，因试验条件限制，以及数值模拟方法操作繁琐、依赖参数较多等缺点[19-20]，目前采用此方法考虑滑带应变软化特性分析坡体稳定性在工程实践中并不具有普遍性。数值模拟和极限平衡方法在滑坡稳定性分析中各有优劣，而将两者结合起来对坡体进行稳定性分析，是一种值得考虑的途径[21]。因此，本文在以往研究基础上，基于弹塑性有限元法获得滑坡体应力场，利用摩尔-库仑强度准则判断滑带不同位置所处应力状态，进而对滑带进行抗剪强度分区，并结合传递系数法计算坡体稳定系数。

1 基本分析原理

1.1 滑带土强度参数分区取值

滑坡的失稳破坏是一个由局部到整体的渐进性破坏过程，其实质是受控于滑带土的应变软化效应。滑带土的应变软化一般模型如图1所示，在滑带土剪切变形(剪应变为γ)过程中，当滑带上某点的剪应力τ达到其峰值抗剪强度τf(相应剪应变为γf)时，该点发生破坏；随着剪切变形发展(γ>γf)，该点土体的抗剪强度逐渐降低，直至达到残余抗剪强度τr(相应剪应变为γr)；随着剪切变形进一步增大(γ>γr)，土体抗剪强度保持为τr不变。因此，在滑带上任一点应变软化过程中，其抗剪强度的变化可分为三种状态，即：峰值强度及其以前的状态(简称峰前状态)、残余强度状态(简称残余状态)以及介于二者之间的过渡强度状态(简称过渡状态)。

图1 滑带土应变软化一般本构模型Fig.1 General constitutive model for strain softening of sliding shear band

根据库仑强度定理，土体抗剪强度可分为与内摩擦角有关的分量(简称为内摩擦分量)和与黏聚力有关的分量(简称为黏聚力分量)组成。实际上，在一定正压力情况下，土体抗剪强度的降低是由于内摩擦角和黏聚力降低所造成的。因此，假设在土体应变软化过程中，其抗剪强度的内摩擦分量和黏聚力分量也具有峰前、过渡和残余状态。这样，针对此3种状态，土体内摩擦角和黏聚力也取相应的不同参数。也即，对于峰前、过渡和残余状态阶段，土体强度参数分别取峰值、过渡和残余参数值。

1.2 滑带分区方法

既然滑带上各点的抗剪强度与该点的应力水平密切相关，因而合理确定滑带土的应力场是正确判断各点所处的强度状态的前提。考虑到实际操作的简单方便性，可采用基于弹塑性本构模型和摩尔-库仑强度准则的弹塑性有限元法确定坡体的应力场。在此基础上，对滑面上的任一点P(相应于条分法中的第j条底面中点，见图2)，根据静力平衡对微元体应力变换，可得该点沿滑面的法向与切向应力σαj、ταj分别为：

(1)

(2)

式中：σxj、σyj、τxyj——P点处应力单元体x面正应力、y面正应力以及x面剪应力(kPa)；

α——P点处滑面切向与竖直方向夹角(°)，其变化范围为0°～90°。

进而根据库仑强度定理，可得该点的峰值抗剪强度τfj为：

τfj=σαjtanφj+cj

(3)

式中，φj、cj——分别为P点处滑面的内摩擦角(°)和黏聚力(kPa)。

图2 堆积层滑坡稳定性分析模型Fig.2 Stability analysis model of bedrock-talus landslide

令无量纲参数β=ταj/τfj，采取如下步骤对滑带进行抗剪强度分区：

(1)假定坡体一稳定系数值Fs，滑带土取峰值强度参数，判断1-β最小值所在的条块i；

(2)对于推移式滑坡，在条块i以上(后缘)的各条块，因其沿滑面方向位移大于第i块，均接近或达到破坏状态。其中，满足剪应力小于或等于残余强度的条块，滑带强度参数取残余值；满足剪应力大于或等于峰值强度的条块，滑带强度参数取峰值；满足剪应力介于峰值与残余强度之间的条块，滑带强度取参数过渡值(如：峰值与残余的均值)。由此，此部分滑带可划分出峰值强度、残余强度、过渡强度区段。在条块i以下(前缘)的各条块，处于非破坏状态，滑带强度参数取峰值。

(3)对于牵引式滑坡，在条块i以下(前缘)的各条块，因其沿滑面方向位移大于第i块，均接近或达到破坏状态。滑带强度参数取值方法同步骤(2)。在条块i以上(后缘)的各条块，处于非破坏阶段，滑带强度参数取峰值。

1.3 坡体稳定系数求解方法

在根据现场工程地质调查判断出滑坡为推移式或牵引式滑动的条件下，按上述方法，一般可将滑带划分为三个区段(含两个区段情况)。根据前述的各区段滑带强度参数不同取值，按传递系数法[22](见式(4)、(5),公式中下标j对应图2中j条块)得到坡体稳定系数计算值Fsc。比较Fs与Fsc，若二者差异较大，则调整Fs值，再从第(1)步开始重新计算，直到稳定系数计算值Fsc与假定值Fs接近(满足工程精度要求)为止。

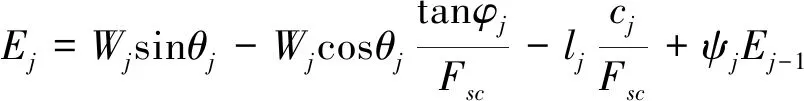
(4)

(5)

式中：Ej、Ej-1——第j、j-1条块的剩余下滑力(kN/m)；

在盾构到达下穿铁路段前，设置100m试验掘进段，通过试验段的盾构掘进调整各项技术参数，对地面变形、深层土体位移等数据进行详细的监测和分析总结，总结最佳盾构施工技术参数，为盾构穿越高速铁路桥提供数据依据[1]。

θj、θj-1——第j、j-1条块滑面倾角/(°)；

Wj——第j条块的自重/(kN·m)；

lj——第j条块滑面长度/m；

cj——第j条块滑面黏聚力/kPa；

φj——第j条块内摩擦角/(°)；

ψj——第j-1与j条块间剩余下滑力传递系数。

实际上，上述方法为数值模拟与极限平衡的组合方法，其优点在于不需滑带土的应变软化试验曲线，只需获得其峰值与残余强度参数即可，在实践中较容易操作。

2 实例分析

2.1 实例一

如图3所示，宝成铁路沿线某中风化砂岩上覆块石土堆积体的潜在滑坡。该潜在滑坡所在区域在地质构造上不存在大的褶皱和断层，构造应力在长期地质作用过程中已释放完成，因此可只考虑重力作用。坡体上覆第四系全新统崩坡积块石质土，下卧侏罗系上统中风化砂岩。根据现场实际勘察，该滑坡为推移式滑坡，坡体主要物理力学参数见表1。

表1 实例一坡体主要物理力学参数

注：括号内为残余值，过渡值取峰值与残余值的均值。

根据第1.2节所述分区方法，首先建立数值分析模型(图4)，模型左右和前后两个边界面采用水平位移约束，底面采用水平和竖向双向位移约束，利用FLAC3D获得坡体应力场。在取Fs=1时，得到滑带分区结果如图3中所示。可见，因坡体后缘产生拉裂区，其抗剪强度取为零；在坡体中后部β=1，说明该区域滑带处于破坏状态；坡体前缘局部β<1，说明该区域滑带处于峰前状态。基于此分区，采用传递系数法计算得到稳定系数为1.039，与假设值误差为3.9%，认为满足精度要求。

图3 实例一横截面示意图及滑带强度分区Fig.3 Sketch map of crosssection of landslide example 1 and its strength partition of shear band

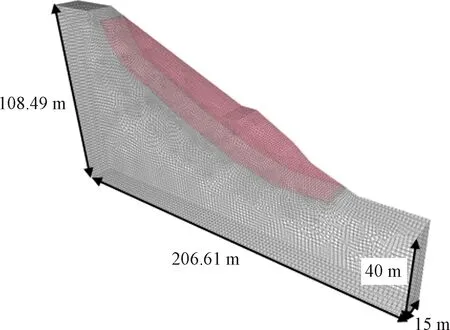
图4 实例一数值分析模型Fig.4 Numerical analysis model of example 1

2.2 实例二

如图5所示，遵义市正安县庙塘镇半边街某中风化粉砂岩上覆碎石土堆积体的潜在滑坡。该滑坡所在区域在地质构造上也不存在大的褶皱和断层，且可只考虑重力作用。坡体碎石土为含黏粒的碎石角砾土，呈棕黄、褐灰等色，硬塑-软塑状；粉砂岩呈棕灰色，成分以石英为主，含暗(黑色)岩屑、黏土矿物，泥钙质胶结，粉粒结构。根据现场勘察，该滑坡为推移式滑坡，主要物理力学参数见表2。

与实例一类似，首先利用FLAC3D获得坡体应力场。然后，采用前述方法得到在取Fs=1.1时滑带分区结果如图5中所示。可见，在坡体中后部β=1，说明此时该区域处于破坏状态；坡体前缘局部β<1，说明该区域处于峰前状态。根据此分区，采用传递系数法计算得到坡体稳定系数为1.19，与假设值误差为8.2%，认为满足精度要求。

表2 实例二坡体主要物理力学参数

注：括号内为残余值，过渡值取峰值与残余值的均值。

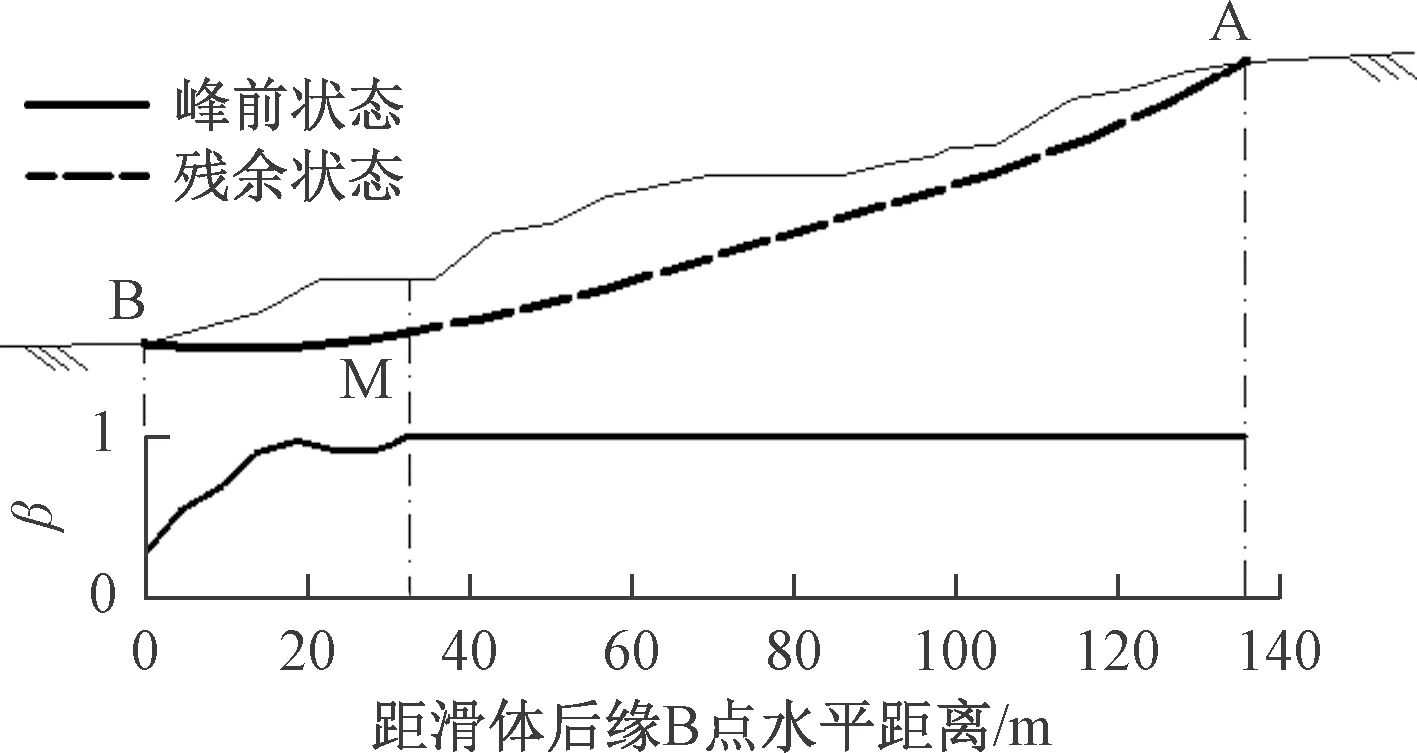
图5 实例二横截面示意图及滑带强度分区Fig.5 Sketch map of crosssection of landslide example 2 and its strength partition of shear band

3 讨论

前面所述的分区方法是在采用理想弹塑性本构模型的有限元法(简称方法Ⅰ)获得坡体应力场基础上实现的。实际上，坡体应力场也可采用考虑应变软化本构模型的弹塑性有限元方法(简称方法Ⅱ)或者近似采用弹性有限元方法(简称方法Ⅲ)获得，前者的数值模型更为复合实际，而后者计算效率更高。为说明获得坡体应力场的不同方法对坡体稳定性分析结果的影响，这里仍针对实例一和实例二，进行3种应力场获得方法的比较。

图6、图7分别为实例一、二的方法Ⅰ、Ⅱ、Ⅲ的滑带分区计算结果。可见，其滑带中后部土体均处于残余状态，前缘局部处于峰前状态。但是，方法Ⅰ、Ⅲ得到的滑带分区均为峰前和残余状态两段，而方法Ⅱ得到的滑带分区还包含了过渡状态段。因此，从实际滑带土强度弱化过程而言，基于方法II的滑带分区方法相对更为合理。

图6 实例一3种获应力场方法的滑带分区结果Fig.6 Results of strength partition of shear band using three methods for stress fields in landslide example 1

三种方法得到的坡体稳定系数如表3所示。表中也同时给出了不考虑滑带强度分区(滑带强度参数取峰值或残余值)的坡体稳定系数计算结果。可见，方法Ⅰ、Ⅱ、Ⅲ得到的稳定系数非常接近，均介于峰值稳定系数(强度参数取峰值)和残余稳定系数(强度参数取残余值)之间。在这3种方法获得坡体初始应力场时，方法Ⅰ采用的是Mohr-Coulomb屈服准则，方法Ⅱ则是在Mohr-Coulomb屈服准则中关联了软化特征，而方法Ⅲ则是采用弹性分析，这对于在峰值强度状态下自然坡体较为稳定的情况(此两实例)，三者获得的坡体应力场差异较小。同时，与此相关的滑带分区总体差异也不大，尤其是对于方法Ⅰ和Ⅲ，两者获得的滑带分区结果几乎一致，方法Ⅱ滑带分区会出现局部较小的过渡状态区。因此，这两个实例分析结果显示这3种方法确定的坡体稳定系数差异较小。

对于实例一、二，就方法Ⅰ而言，考虑滑带分区得到的稳定系数比峰值稳定系数分别小14.1%、21.6%，比残余稳定系数分别大1.1%、10.2%。

表3 3种获得应力场方法得到的两坡体稳定系数Table 3 Safety factors by three methods for stress fields in the two landslide examples

图7 实例二3种获应力场方法的滑带分区结果Fig.7 Results of strength partition of shear band using three methods for stress fields in landslide example 2

4 结论

(1)基于弹塑性有限元分析法获得坡体应力场，根据滑带上任一点剪应力与抗剪强度大小关系，着眼于滑带土的峰值强度、过渡强度和残余强度，给出了包括推移式滑坡与牵引式滑坡的滑带抗剪强度分区方法。

(2)根据滑带分区方法与传递系数法，给出了考虑滑带土不同区段抗剪强度参数取不同值的坡体稳定性分析方法。

(3)实例分析表明，确定坡体应力场的基于理想弹塑性本构模型、考虑应变软化本构模型的弹塑性有限元方法和弹性有限元方法，所得到的考虑滑带强度参数分区的坡体稳定系数差异较小。同时，考虑滑带分区得到的坡体稳定系数比不考虑分区的峰值稳定系数约小14.1%～21.6%，比残余稳定系数约大1.1%～10.2%。