BFRP锚杆加固斜坡对地震动的响应特征——以功东高速响水河边坡为例

王秋懿，吴红刚，张金江，李天能

(1.云南省交通投资建设集团投资有限公司，云南 昆明 650228； 2.中铁西北科学研究院有限公司，甘肃 兰州 730000)

0 引言

BFRP锚杆是以玄武岩纤维为增强材料，环氧树脂为基体材料，采用纤维浸渍含有固化剂的环氧树脂胶液，经过拉挤而形成的一种新型材料。具有抗腐蚀性好、耐久性好、抗拉强度高、低松弛性及抗震性能优越等特点。同时，由于BFRP筋材的弹性模量较钢筋低，约为钢筋的1/4，作为锚杆使用相对钢锚杆而言，可较少的影响锚固体与围岩的黏结状态，也具有更好的适应坡体变形的能力[1-2]。

目前，因其优越的物理-化学性能，BFRP筋已经越来越多的应用于边坡锚固设计和工程建设当中，但对于BFRP锚杆的研究大多停留在材料力学性能应用层面，曹晓峰等[3]、杨国梁[4]、高先建等[5]、王洋[6]从锚杆直径、锚固段长度和锚固地层岩性等方面通过一系列现场抗拉伸试验、抗剪试验，研究了玄武岩纤维锚固系统极限抗拉强度、荷载位移关系、杆体轴力分布和剪应力分布状态等，对BFRP锚固结构的应用起到了理论的推动作用。但是这些试验都是针对单根锚杆锚固系统进行的，并未对BFRP锚固系统和边坡的协同工作性能展开研究，尤其地震作用下BFRP锚固边坡的结构-边坡协同工作性能方面的研究目前还很滞后。

高先建[7]通过FLAC3D数值模拟计算了BFRP锚杆和钢筋锚杆加固基坑边坡的支护效果，认为BFRP锚杆可以有效的加固边坡，较好的控制边坡位移，且加固效果与钢筋锚杆相当，边坡破坏模式与钢筋锚杆加固边坡相同。王安福等[8]通过实际工程应用中BFRP锚杆(索)受力特征长期监测，并与传统钢筋锚杆和钢绞线锚索受力进行对比，验证BFRP锚杆(索)在公路岩质边坡支护中的可行性。赵文等[9]将BFRP筋作为锚杆，对其抗拉强度设计值、与砂浆黏结强度取值进行了实验研究，通过BFRP筋材和钢筋锚杆加固土坡的现场对比试验，分析了BFRP锚杆加固土质边坡的效果，表明两种锚杆受力和边坡变形类似，验证了BFRP筋作为岩土支护锚杆的适用性。

通过上述研究发现，对于BFRP锚杆在动力情况下支护边坡的研究还有所欠缺，为了明确地震作用下BFRP锚固系统加固边坡的抗震效果，本文通过振动台试验的方式，对无支护边坡与BFRP锚固边坡在EL-Centro地震波作用下的加速度及动应力响应情况进行了研究，旨在为高速公路边坡的抗震设计提供一定的理论支撑。

1 试验方案及过程

1.1 振动台模型试验概况

本次试验场地位于甘肃省地震局黄土地震工程研究室，振动台台面有效尺寸为4 m×6 m，试验所用的模型箱是由钢板、型钢和有机玻璃制作的刚性箱，尺寸为2.85 m×1.45 m×1.8 m，为了便于填料，模型箱一端开口，配备可自由拆卸的挡板。为了减小振动波在边界的反射作用，在地震波水平传播方向的箱体后壁内衬3 cm厚的缓震泡沫，用来模拟吸波材料[10]。采用在线迭代控制加载方式，振动台工作输入信号包括：位移时程、速度时程、加速度时程、反应谱和功率谱，可以输入规则波、随机波、地震波和人造波等。

试验模型依托工点为云南省功东高速公路沿线里程K5+660附近的响水河路堑边坡，边坡高度为29.5 m，边坡坡面形式为三级坡，采用锚索框架结构作为边坡加固措施，该区域位于小江断裂带影响范围内，是我国地震活动多发地带，地震基本烈度高达Ⅸ度，因此开展该地区边坡的地震动力响应模型试验具有重要意义。

1.2 模型相似设计

根据此次试验条件和目的，本文在全面、综合考虑各种因素的基础上，主要考虑选取试验的9个关键物理量：容重γ、位移δ、应变ε、几何尺寸l、应力σ、泊松比u、弹性模量E、黏聚力c和内摩擦角φ，按相似理论，借助因次分析法推导模型与原型的相似准则[11]，然后按相似判据进行模型设计和试验，其函数关系式为：

f(l，δ，γ，ε，E，σ，u，c，φ)=0

(1)

以几何尺寸l和弹性模量E为基本量纲的物理量，利用相似“π定理”式(1)变为：

f1(π1，π2，π3，π4，π5，π6，π7，π8，π9)=0

(2)

根据力学现象相似准则：

(3)

1.3 模型试验制作

(1)岩土体相似材料

相似材料的设计是开展物理模型试验的重要环节，其设计合理与否直接决定着模型试验结果能否准确真实的反映工程原型物理力学特性。振动台试验相似材料与一般的地质力学相似材料不同，它要求模型相似材料的动应力-动应变特性、动剪切模量衰减特性、阻尼特性、剪切波速、密度、不固结不排水强度等特性与原型材料满足相似性要求[12]。

本次模型试验依托响水河工点，模型边坡上覆地层为全风化玄武岩，岩块之间黏结强度低，岩体破碎现象明显。模型制作时将边坡岩块用河砂模拟，岩块间的胶结物用黏性土模拟，添加石膏粉进行混合搅拌，通过改变石膏粉的含量和材料密度来调节模拟材料参数。通过大量室内剪切试验和单轴压缩试验，采用黏性土∶河砂∶石膏粉∶水=5∶10∶1∶1的质量配合比模拟全风化玄武岩地层，其物理力学室内试验参数统计见表1。

表1 试验土层材料物理力学参数

(2)相似结构

试验选用直径为4 mm的BFRP纤维筋作为锚杆，其弹性模量为200 GPa，锚杆总长度为100 cm，锚固段长度为40 mm，外漏纤维筋长10 cm，用于锚固。框架梁采用松木条制成，水平向横梁和竖向纵梁的截面尺寸均为3 cm×2 cm。在边坡体制作完成后，将埋设在坡体内的PVC管人力拔出，在模型土体中植入锚固体，然后安装用松木条制作的框架梁，最后人工张拉锚索自由端锁定，锚杆布设过程如图1所示，制作完成的试验模型见图2。

图1 锚杆布置安装Fig.1 Arrangement and installation of anchor rod

图2 模型制作完成Fig.2 The completed Model

1.4 模型监测点布置和制作过程

试验中采集了边坡动土压力值及加速度值，各种传感器在使用之前均已进行过现场标定，从而保证测量数据的准确。监测点布设原则和位置如下所述，其示意图见图3。

图3 模型尺寸及测点位置Fig.3 Model size and measurement points

(1)加速度传感器

采用DH301系列三向电容式加速度传感器(图4)。为研究边坡潜在滑体形成过程内软弱夹层对坡体的加速度高程响应特性，分别在距坡面40 cm处和距坡面5 cm处由下到上等间距布置加速度传感器，另外在坡脚自由场和振动台台面各布置1个加速度测点。振动台模型试验时共布设20个加速度传感器。

图4 三向电容式加速度传感器Fig.4 Three-way accelerometer

(2)动土压力传感器

动压力传感器为CYY9型土壤岩石压力传感器(图5)。该传感器输出信号范围为0～5VDC(中间点为2.5VDC)，准确度等级为0.25%，测量范围为-500～+500 kPa。为了研究边坡中水平向动土压力在振动过程中的响应规律，分别在每级坡中部，据坡面40 cm和80 cm布置土压力计。

图5 CYY9土壤岩石压力传感器Fig.5 CYY9 soil and rock pressure sensor

1.5 地震波输入及加载工况

功东高速公路位于小江断裂带附近，历史上多次发生过大地震，为了研究公路沿线高边坡的地震动稳定性和新型支护结构的抗震性能。本次试验采用EL-Centro 波进行加载。相似试验中加载波形也需要根据模型试验设计的相似系数对加载时间和频率含量进行修正，按照本次试验的相似系数20，对地震波进行压缩(表2)。

表2 输入地震波相似关系表

地震波相似处理后，加载波形的频率为原始波形频率的λ0.5倍，即4.47；加载波形的加载时间为原始波形频率的1/λ0.5倍,即0.224；加载波形的振幅不变。原始波形的卓越频段均在0.1～10 Hz,而记录时间为40 s，因此修正后的加载波形频段为0.447～44.7 Hz，(此频段上限不超过振动台的工作频段50 Hz，)，加载时间为8.94 s。压缩后输入地震波时程曲线如图6所示。

本文研究区处于高烈度地区，故将最高输入加速度峰值设定为1.0g，采用逐级地震加速度峰值的方式进行[13]，加速度峰值从0.1g到1.0g，具体加载工况见表3。

图6 压缩后的EL-Centro地震波加速度时程曲线Fig.6 Acceleration time history curve of compressed EL-Centro seismic wave

表3 输入地震波加载方式

Table 3 Loading mode of input seismic wave

工况波形加载方向PGA1正弦扫频水平(X)0.05 g (0.1～50 Hz)3EL wave水平(X)0.1 g5EL wave水平(X)0.2 g7EL wave水平(X)0.4 g8EL wave水平(X)0.6 g10EL wave水平(X)0.8 g12EL wave水平(X)1.0 g14正弦扫频水平(X)0.05 g (0.1～50 Hz)

2 试验结果及分析

2.1 试验现象

在加速度峰值小于等于0.6g时，试验现象不显著，主要为未支护侧坡面出现裂缝和轻微掉块(图7)，坡体与背部减震泡沫有轻微分离，侧面观察无内部裂缝，表现为整体轻微位移。

图7 0.6 g时无支护侧的三级坡坡面裂缝Fig.7 Cracks on grade III slope without supportinig while the acceleration is 0.6 g

当加速度峰值为0.8g时，未支护侧整体位移加剧，坡面裂缝继续发育，各级坡脚出现横向贯通裂缝(图8)，二级坡面约45°的斜向贯通裂缝，坡体中上部侧面出现斜裂缝；支护侧第三级坡坡脚和模型侧面裸露处出现掉块。

图8 0.8 g时坡面裂缝Fig.8 Cracks on slope surface while acceleration is 0.8 g

到1.0g时，无支护侧坡体破坏严重，各级坡已无明显分界(图9)；支护侧的坡体形态保存较好，破坏主要为坡脚的0.5～1.0 mm横向贯通裂缝和裂缝附近的局部掉块，位移在强震中表现为整体位移。可以看出经过BFRP框架梁加固的坡体在强震作用下的整体稳定性好。

图9 1.0 g时坡面破坏情况Fig.9 Failure of slope surface while acceleration is 1.0 g

2.2 加速度响应特性

为研究边坡响应加速度的放大效应，将边坡体内的加速度放大系数定义为各测点加速度峰值与坡脚自由场处测点的加速度峰值之比。此处以不同工况下BFRP锚杆框架结构支护和未支护斜坡坡体内及坡顶测点的加速度放大系数进行说明：如在地震波作用下，坡体内某一测点水平向加速度的最大绝对值为max(水平)，而对应时刻的台面测点加速度的最大绝对值为max(台面)，则加速度放大系数a为：

在EL波各加载工况下，框架支护坡面加速度放大系数与台面监测地震波峰值的关系(图10)。图10为输入水平向(X向)作用地震波峰值增大的过程中，不同高程位置坡面的加速度放大系数随输入地震波加速度峰值的变化趋势，整体呈现“台阶状”上升。当峰值加速度为0.2g时加速度放大效应的增长趋势明显开始出现减小。在高程为55 cm和105 cm处的坡面加速度放大系数增长趋势较缓，在三级坡坡面和坡顶位置处的加速度峰值放大系数增长幅度较大。当输入地震波峰值为0.1g、0.2g、0.4g时加速度放大系数增长趋势相同，在加速度为0.2g时，各高程加速度放大系数均较小，其原因是加速度为0.2g时，支护结构对坡面加速度的放大效应起到了一定的抑制作用。

图10 EL波激励时框架支护坡面加速度放大系数 与输入地震波峰值关系Fig.10 Relation between acceleration amplification coefficient and peak value of input seismic wave (excited by EL wave)

高度在155 cm处的加速度放大系数随输入地震波峰值加速度的增加而呈“锯齿状”增加趋势，具体表现为0.1g～0.2g、0.4g～0.6g为下降段，0.2g～0.4g加速度放大系数处于上升阶段，0.6g以后加速度放大系数基本显示处大幅度的上升趋势；高度在180 cm处的加速度放大系数随着输入波加速度峰值的增大而增加，具体表现为0.1g～0.2g为下降段，0.2g～0.6g加速度放大系数上升段，0.6g～0.8g为下降段，0.8g以后加速度放大系数呈上升趋势。

通过分析试验过程中坡体裂纹及坡表破坏现象，可以发现边坡坡表加速度放大系数沿高程严格增大，导致该现象的原因是由于边坡顶部在地震作用下产生了局部破坏，从而导致坡体受力状况和几何形态的改变对加速度的传播规律造成了影响。例如：第三级坡在输入地震动过程中震动剧烈，坡顶逐渐产生横向裂纹，随着地震加速度峰值的增大，裂缝逐渐产生贯通；第二级坡坡面和第三级坡坡面均产生横向贯通裂缝。

在EL波各加载工况下，无支护台面监测地震波峰值与坡面加速度放大系数的关系如图11所示。随着输入波加速度峰值的增大，不同高程位置坡体的加速度放大系数随输入地震波峰值加速度的增加近似呈稳定上升趋势。当峰值加速度为0.2g时，高程为105 cm、155 cm、180 cm的位置处加速度放大系数稍微有所降低，从55 cm往上，高程对加速度放大系数的影响有所降低。

在输入地震波峰值加速度在0.1g时，高程105 cm处的加速度放大系数比高程155 cm处的大，即二级坡坡面的加速度放大系数大于三级坡坡面的加速度放大系数，说明在无支护的斜坡上斜坡的坡腰最先承受较大的地震动力影响。

从0.2g～0.6g加速度放大系数沿高程和输入地震波峰值呈增大趋势，到输入地震波峰值加速度为0.8g时高程155 cm处的加速度放大系数最大。当输入加速度峰值大于0.8g后斜坡坡顶产生贯通裂缝，岩土体整体性较差，坡顶位置的加速度放大系数呈“锯齿状”的增长趋势；在高程为155 cm处的坡面加速度放大系数增长趋势平稳，三级坡坡面振动剧烈，有崩塌的趋势；在高程为105 cm处的坡面加速度放大系数在输入地震波峰值达到1.0g时产生骤降，二级坡坡面发生了滑动，坡体表面埋置的加速度传感器出露。

图11 EL波激励时无支护坡面加速度放大系数 与输入地震波峰值关系Fig.11 Relation between acceleration amplification coefficient of unsupported slope and peak value of input seismic wave (excited by EL wave)

通过上述分析可得，当输入加速度峰值相同时，对应的高程处，无支护侧坡面的加速度放大系数比支护侧的加速度放大系数要大，表明框架锚固结构对边坡的加速度放大系数起到了有效地抑制作用，从而提高了边坡的整体稳定性。

2.3 应力响应特性

地震波持续过程中，在动静力场耦合作用下岩土体单元应力时刻发生变化，从一点的应力状态来看，单元体应力与测点水平向加速度响应有直接关系。本次试验对BFRP锚固边坡和未支护边坡坡体内不同高程和埋设深度的土压力进行监测，得到边坡体空间位置的应力状态，通过摩尔库伦强度准则对坡体内不同位置应力屈服状态进行判断。首先测的了正弦扫频波作用下边坡自振时的应力状态，随着输入地震波峰值加速度的增大，应力状态不断发生变化，如图12～图14所示。

图12 锚固边坡断面Ⅰ应力分布Fig.12 Stress distribution of at sectionⅠ in slope supported with anchorage

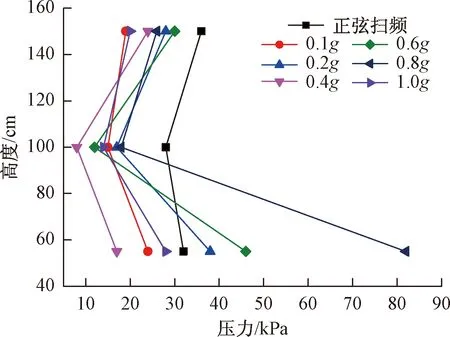
图13 锚固边坡断面Ⅱ应力分布Fig.13 Stress distributionat section Ⅱ in slope supported with anchorage

图14 未支护边坡断面Ⅰ应力分布Fig.14 Stress distribution at section Ⅰof unsupported slope

对比锚固边坡监测断面Ⅰ和监测断面Ⅱ的应力分布可以观察到，锚固边坡监测断面Ⅰ的压应力最大值出现在二级坡坡后(高度105 cm)，输入地震波为正弦扫频时该测点压应力最大，随着输入地震波峰值加速度的增大，测点压应力值逐渐减小。其他高度位置的测点压应力值较小，随着加速度增大基本不发生变化。

锚固边坡监测断面Ⅱ的压应力最大值出现在一级坡(高度55 cm)和三级坡(高度155 cm)坡后相对位置，除输入正选扫频外，其他加速度峰值地震波作用下边坡应力变化不大，规律性也不太明显，在输入地震波达到0.8g后一级坡后土体压应力突增，可能发生了剪切应力屈服。

由于未支护边坡监测断面Ⅱ有一处土压力传感器发生故障，监测数据无效，因此仅对监测断面Ⅰ的应力分布做出分析，可以看出监测断面Ⅰ的压应力最大值出现在三级坡坡后，其他位置岩土体应力没有明显差别，表明无支护边坡在地震波作用下，上部岩土体首先发生张拉应力屈服，其他位置应力状态变化较小。压应力最大值出现在输入正弦扫频的时候，可认为此时的压应力与该测点单元体在静力作用下受到的应力相同。随着输入地震波峰值加速度的增大，压应力逐渐减小，其原因是由于岩土体受张拉作用而导致的。

3 结论

以功东高速响水河边坡为试验原型，通过振动台试验，对无支护边坡与BFRP锚固边坡在不同峰值加速度地震波作用下的加速度放大系数及动应力变化情况进行了研究，所得结论如下：

(1)当输入地震波加速度峰值相同时，对应的高程处，无支护侧坡面的加速度放大系数比支护侧的加速度放大系数要大，表明BFRP锚固结构对边坡的加速度放大系数起到了有效地抑制作用，从而提高了边坡的整体稳定性。

(2)由于地震波在坡体内传播介质不均匀的原因，使得坡面各测点加速度放大系数随输入地震波加速度峰值的增大并非呈现线性增加的关系，而是一种“锯齿状”的变化趋势。

(3)BFRP锚固结构加固边坡二级坡坡面附近单元体压应力最大，坡体内部在三级坡后单元体压应力最大，而无支护边坡坡面主要承受边坡上部的拉应力，边坡体内单元受力并不均匀，表明BFRP锚固结构可以改变边坡单元体的受力状态。