降雨条件下建筑边坡稳定性的云模型评价方法

陈忠源，戴自航

(1.福州大学，福建 福州 350116；2.福州外语外贸学院，福建 福州 350202)

0 引言

随着城镇化的建设与发展，越来越多的建筑物依山而建。一旦发生滑坡，就有可能给边坡周边居民的生命和财产造成损失。大量的研究表明，降雨是导致边坡失稳的主要诱因之一。因此有必要对降雨条件下的建筑边坡稳定性进行分析评价，以便相关人员及时做好预警工作，最大限度降低滑坡造成的损失。目前，用于描述降雨情况的参数主要有降雨强度、降雨历时及前期降雨量等。随着这些降雨参数的增大，滑坡的可能性也越大。而如何确定滑坡发生时这些降雨参数的下限临界值，也即降雨阈值，是本文研究的重点内容之一。

1980年，CAINE[1]首次提出了降雨强度与降雨历时的降雨阈值公式。随后，国内外专家学者们也进行了一系列的探讨研究。GUZZETTI等[2]提出了累积有效降雨量与降雨强度的阈值公式。NAIDU等[3]利用组合聚类与回归分析方法对印度的喀拉拉邦的Amboori边坡进行分析，提出了5天前(x变量)与日降雨量(y变量)之间的阈值公式。GLADE T[4]通过分析土壤的临界含水量，建立了关于前期日降雨量的模型，以对降雨阈值进行确定。林鸿州等[5]通过降雨诱发土质边坡失稳的模型试验及已有研究成果，揭示了降雨入渗对边坡稳定性的作用机制，并建议采用降雨强度与累积雨量作为雨量预警基准所需的参数。付世军等[6]利用南充地区加密区域气象观测资料和地质灾情数据，使用基于衰减系数的有效降水量和I-D关系阈值相结合的方法，研究得出不同时效致灾雨量阈值。还有GERMAIN等[7]、黄健敏等[8]、刘海知等[9]、丁桂伶等[10]、周雨等[11]、高波等[12]、ROSI等[13]许多专家学者开展了一系列的研究工作。

目前，降雨阈值的确定方法，主要分为经验型降雨阈值和物理型降雨阈值[14]。经验型降雨阈值的确定主要通过分析统计分析滑坡发生时的降雨特征，以经验为主，无须严格的公式推导。物理型降雨阈值的确定主要通过岩土体的地质特征、降雨入渗情况以及边坡失稳机理等因素的分析，利用公式推导得到。但是经验型降雨阈值侧重以经验为主，没有考虑各边坡特有的地形、地质以及人类活动等情况，较难应用于某一具体的边坡。物理型降雨阈值主要针对于某一具体边坡[5]，而且考虑的边坡岩土体以及降雨参数较少，较难推广应用至其他边坡。

鉴于上述原因，本研究以建筑边坡为研究对象，引入云模型的评价方法，综合考虑边坡岩土体的主要地质特征、降雨强度、降雨历时以及前期降雨量等因素，建立建筑边坡稳定性评价体系。根据该评价体系对不同降雨工况下的建筑边坡稳定性进行评价，确定出滑坡时各参数的降雨阈值方程。

1 云模型简介

云模型是李德毅等[15]提出的对概念的随机性和模糊性进行有效处理的一种工具。由于降雨阈值的确定较难确定某一具体数值，具有一定的模糊性，因此本文引入该方法进行分析。期望Ex、熵En和超熵He三个参数可用来表示云模型的数字特征。其中：Ex表示云滴在论域空间分布的期望；En是定性概念不确定性的度量，也即熵；He是熵的不确定性的度量，即熵的熵[16]。该三个参数可采用式(1)计算得到。

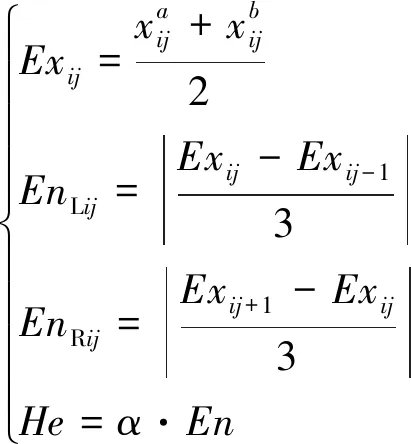
(1)

式中：Exij——某一评价指标zi(i=1，2，…，n)对应的评价等级sj(j=1，2，…，n)的期望；

EnLij——某一评价指标zi(i=1，2，…，n)对应的评价等级sj(j=1，2，…，n)左半云的熵；

EnRij——某一评价指标zi(i=1，2，…，n)对应的评价等级sj(j=1，2，…，n)右半云的熵；

α——调整云模型的雾化程度指标。

2 工程概况

金龙花园小区位于福建省南平市延平区来舟镇游地村，是建在坡顶平台上的2～3层砖混结构居民住宅区。该边坡高约15～20 m，坡长约80 m，坡度约40°～45°，坡脚为316国道，坡脚高程111.10～112.50 m。该地区多年平均降雨量1 500 mm，场地区地下水位埋置高程为103.91～108.92 m。根据野外钻探取芯肉眼鉴别，结合场地原位测试和室内土工试验成果综合分析，在钻探控制深度范围内各岩土层主要特性参数如表1所示。

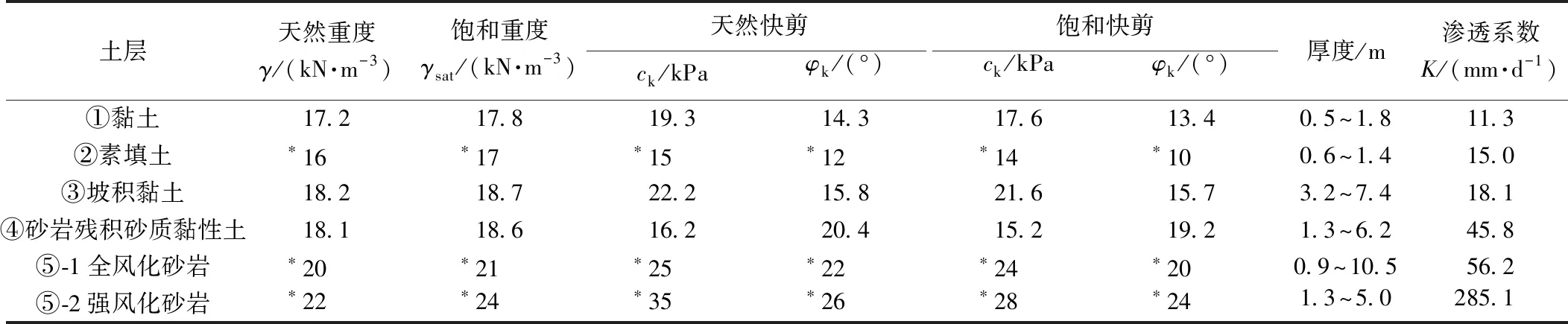
表1 金龙花园小区边坡场地内岩土层特性参数

备注：带*号为经验值。

3 建立基于云模型的建筑边坡稳定性评价体系

3.1 确定分级标准及评价指标

参考《建筑边坡工程技术规范》(GB50330—2013)中的边坡稳定性状态划分，将其划分为稳定(Ⅰ级),基本稳定(Ⅱ级),欠稳定(Ⅲ级),不稳定(Ⅳ级)四个等级。在指标的选取方面，综合考虑前人相关研究成果以及岩土工程勘察报告常用的指标参数，选取坡高H、坡角β、水位埋深与坡高的比值Kh、重度γ、黏聚力c、内摩擦角φ、渗透系数K、降雨历时T、降雨强度I、前期降雨量P这10个参数作为建筑边坡稳定性评价的云模型的指标。由于建筑边坡含有多种岩土层，各岩土层参数不一，且目前学术界对上述降雨参数的定义尚未统一，本文对上述参数定义如下：

坡高H：取边坡的平均坡高。

坡角β：取边坡的平均坡角。

水位埋深与坡高的比值Kh：取降雨诱发滑坡前该边坡的平均稳定水位与平均坡高的比值。

重度γ：取该边坡各岩土体以其平均层厚为权重值的加权平均重度。因本文研究降雨条件下的稳定性，视各岩土层均达到饱和状态，故均取其饱和重度。

黏聚力c：取该边坡各岩土体以其平均层厚为权重值的加权平均黏聚力，本文取饱和快剪试验条件下的黏聚力。

内摩擦角φ：取该边坡各岩土体以其平均层厚为权重值的加权平均内摩擦角，本文取饱和快剪试验条件下的内摩擦角。

渗透系数K：取该边坡的等效垂直渗透系数，各岩土体的层厚取其平均层厚。

降雨历时T：取当日降雨量均大于1 mm/h的连续降雨历时。

降雨强度I：取当日历时内的平均雨强。

前期降雨量P：取当日降雨前15天内的有效降雨量总和，按下式计算[17]。

P=aR1+a2R2+…anRn

(2)

式中：Rn——降雨诱发滑坡前n日当天降雨量；

a——有效降雨系数，根据相关文献[17]的统计分析研究建议取0.8。

3.2 确定评价指标在各稳定性状态中的分级区间及权重

在前人相关研究基础上，结合《建筑边坡工程技术规范》以及各参数的实际情况，对各评价指标在相应稳定性状态中的分级区间进行划分，具体如表2所示。同时采用改进的熵权层次分析法得到各评价指标的最终权重(表2)。

表2 建筑边坡稳定性评价指标各等级区间及权重

3.3 生成评价指标在各稳定性状态中的综合隶属度云模型

将表2的各评价指标等级区间代入式(1)即可计算出各评价指标的云模型参数。根据相关参考文献建议，本文的α取值0.1En。笔者在MATLAB程序语言平台上开发了综合隶属度云模型程序。该程序可根据得到的云模型参数生成各评价指标相对应的综合云模型。其综合云模型的部分matalab语句有[16]：

Z1=zeros(2,N);

for i=1∶N

E_n1=normrnd(En1,He,1,1);

Z1(1,i)=normrnd(Ex1,E_n1,1,1);

Z1(2,i)=exp(-(Z1(1,i)-Ex1)^2/(2*E_n1^2));

if Z1(1,i)>Ex1

Z1(2,i)=1

end

end

节取坡高和黏聚力指标的综合隶属度云模型如图1和图2所示。对于图1的坡高指标，从左到右的四个非对称正态云模型分别对应稳定、基本稳定、欠稳定以及不稳定四个状态。而对于图2的黏聚力指标则刚好相反。该综合隶属度云模型可以较为直观地表现某一实测数据在各稳定性状态的隶属度情况。如当坡高为12 m时，从图1即可直观看出该值隶属于基本稳定的状态可能性最大。

图1 坡高隶属于各稳定性状态的综合云模型Fig.1 Comprehensive cloud model of slope height attached to various stability grades

图2 黏聚力隶属于各稳定性状态的综合云模型Fig.2 Comprehensive cloud model of cohesive strength attached to various stability grades

4 确定边坡欠稳定和不稳定状态的降雨阈值方程

对上述各综合云模型进行数据拟合，可得到不同稳定性状态的实测数据隶属度函数。以图1的坡高指标为例，当其实测坡高位于[15，25]区间时，其隶属于基本稳定和欠稳定状态的隶属函数如式(3)所示。

(3)

式中：x——各指标实测值；

fⅡ(x)和fⅢ(x)——分别表示实测指标值在基本稳定和欠稳定状态云模型中的隶属度。

本工程边坡平均坡高为16.9 m，代入式(3)可得，其在基本稳定和欠稳定状态的隶属度分别为0.85和0.05。

同理可计算出表1中边坡各已知评价指标在各稳定性状态的隶属度。而上述评价指标中，降雨阈值的三个参数T、I、P均为未知数，对于降雨历时T，本文以1.2 h为步长，分别设T=1.2、2.4、3.6…60代入计算。对于降雨强度I，本文以2 mm/d为步长，分别设I=2、4、6…130代入计算。对于前期降雨量P，本文以5 mm为步长，分别设P=5、10、15…250代入计算。利用MATLAB程序语言平台对上述不同的T、I、P情况进行任意组合，可得不同情况下的隶属度。其次将所有10个指标的隶属度分别乘以其各自权重，可得到不同的指标的综合隶属度。最后将指标的综合隶属度按不同稳定性等级相加，可得到该边坡在各稳定性等级的综合隶属度。根据最大隶属度原理，综合隶属度最大值所在的稳定性等级即可判定为该边坡的稳定性等级。

随着参数T、I、P的增加，边坡的稳定性状态由稳定逐渐变为不稳定。选取边坡稳定性状态为欠稳定时，所有不同取值中参数T的最小取值及I、P的相应取值，参数I的最小取值及T、P的相应取值，参数P的最小取值及T、I的相应取值三种情况做为该边坡由基本稳定状态过渡到欠稳定状态时的临界值。对于边坡的不稳定状态亦是同理。结果如表3所示。

将表中各参数的取值当做坐标点，分别设A(3.6，34，140)、B(15.6，4，140)、C(14.4，36，10)、D(3.6，74，235)、E(10.8，10，235)、F(52.8，114，10)。则A、B、C三点可形成一个平面，求解可得α：11.2T+4.48I+P=332.76，该平面即为该边坡由基本稳定状态过渡到欠稳定状态的临界面。同时D、E、F三点可求解出γ：4.19T+0.47I+P=284.96，该平面即为该边坡由欠稳定状态过渡到不稳定状态的临界面。各临界面如图3所示。

表3 临界降雨参数取值所对应的评价结果

设fⅡ—Ⅲ(T,I,P)=11.2T+4.48I+P-332.76，fⅢ—Ⅳ(T,I,P)=4.19T+0.47I+P-284.96。从图3可以直观看出，当T、I、P较小时，即fⅡ—Ⅲ(T,I,P)<0时，该边坡处于稳定或基本稳定区。随着T、I、P逐渐增大，达到fⅡ—Ⅲ(T,I,P)=0时，该边坡开始达到欠稳定状态。当fⅡ—Ⅲ(T,I,P)>0，且fⅢ—Ⅳ(T,I,P)<0时，该边坡处于欠稳定区。当fⅢ—Ⅳ(T,I,P)=0时，该边坡开始达到不稳定状态并将处于不稳定区。从图3中也可看出，当T、I、P较小时，边坡由欠稳定状态过渡到不稳定状态，三个降雨参数过渡的区间也较大，随着T、I、P逐渐增大，过渡的区间逐渐减小。当达到8.01T+4.01I=47.8平面时，边坡的稳定性直接由基本稳定状态到达不稳定状态，没有欠稳定状态的“缓冲期”了。又因达到不稳定状态的最低条件为T=3.6 h且I=10 mm/d，故上述两平面相交的必要条件为T≥3.6且I≥10。当T、I、P继续增大并超出两临界面交线范围，则不再有欠稳定状态，均判定为不稳定状态。

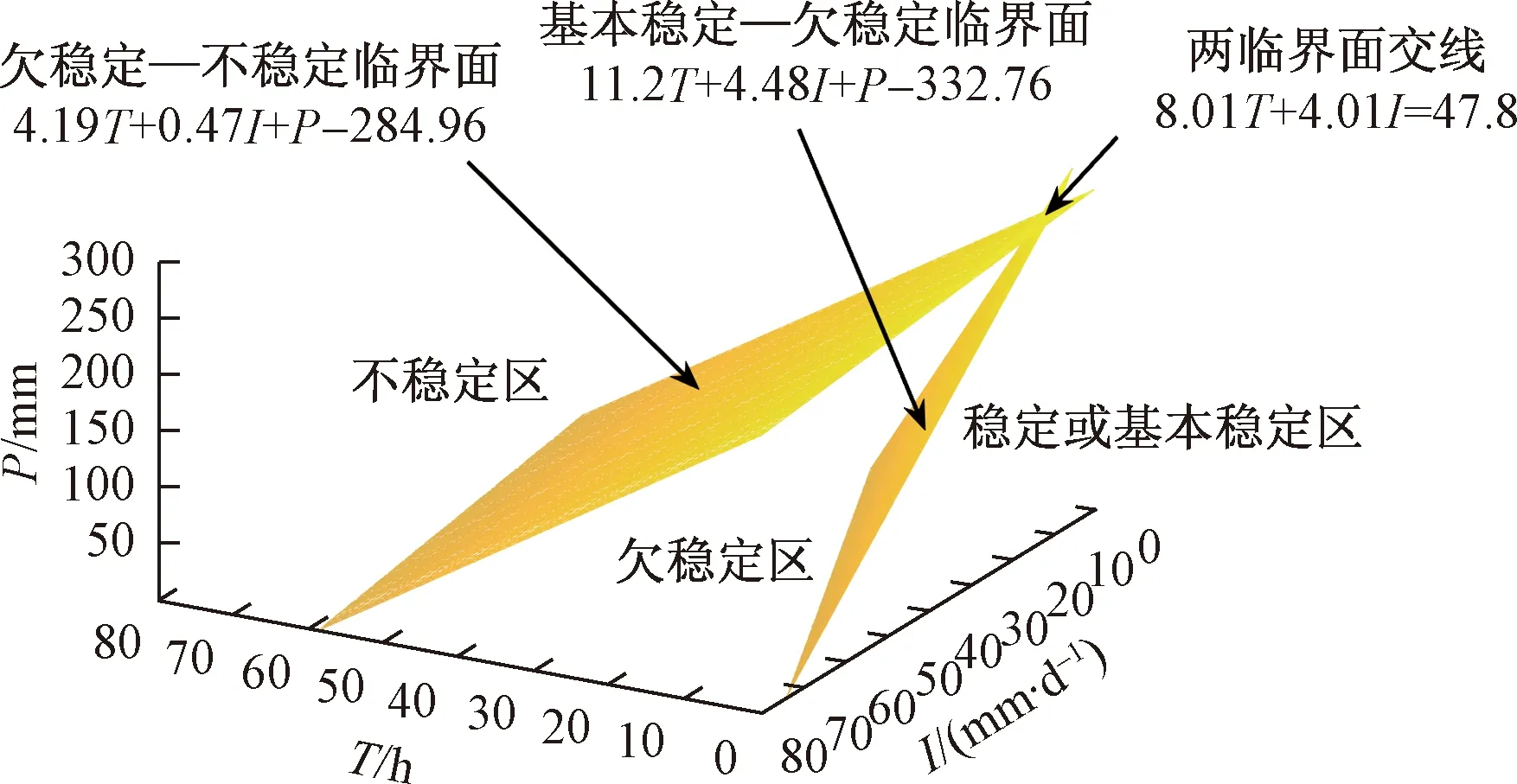
图3 边坡各稳定状态分区及降雨阈值临界面Fig.3 The zoning and interface of slope stability

5 工程实例验证

根据金保明[18]提供的气象资料，前述南平延平区来舟镇2010年6月13日至2010年6月18日的日降雨量分别为78.5 mm、161.5 mm、84.5 mm、4.5 mm、56 mm、143.5 mm。可以看出该边坡分别于2010年6月13—15日和6月17—18日发生了两场大暴雨。但根据该边坡岩土工程勘察报告，该边坡仅于2010年6月18日在暴雨条件下沿残积黏性土层发生滑坡，而未提及6月13—15日有滑坡产生。从降雨强度及历时来看，6月13—15日的第一场雨比6月17—18日的第二场雨大，却没有发生滑坡，由此可以推断6月13日之前降雨较少，故本文视6月13日之前的前期雨量P为0，而6月13日当日及之后的前期降雨量可用式(2)计算。因该两场均为暴雨，本文视6月13—15日以及6月17—18日5日的24 h期间降雨强度均大于1 mm/h，故降雨历时均取24 h。而6月16日当天降雨量仅为4.5 mm，属于天气转好的情况，为方便计算，本文视当日没有存在降雨量大于1 mm/h的时间段，对该日的降雨历时按0考虑。最终可得到6月13—6月18日该边坡的稳定状态(表4)。

表4 边坡的稳定状态分析结果与实际情况对比

从表4可以看出，6月13日当天的日降雨量达到78.5 mm，但由于前期降雨量为0，故边坡稳定状态为欠稳定。6月14日当天的日降雨量达到161.5 mm，加上6月13日的前期降雨量，其状态为欠稳定，且即将达到不稳定状态。6月15日当天的日降雨量达到84.5 mm，加上前两天的累积降雨量，其状态于6月15日23∶59前达到不稳定状态，但实际情况是该边坡6月15日当天无滑坡记录。本文认为6月16日当天的日降雨量为4.5 mm，也即天气转好，所以6月15日当天的降雨强度大于1 mm/h的降雨时段应该少于24 h。而本文以24 h计算，故分析结果与实际情况有所偏差。6月16日天气转好，连续降雨历时视为0，所以即使该日的前期降雨量达到211.15 mm，但其稳定状态为基本稳定。6月17日又开始降雨，该边坡的状态转变为欠稳定状态。6月18日继续降雨，当天的日降雨量达到143.50 mm，前期降雨量也达到了182.52 mm，此时边坡的稳定状态变为不稳定。根据岩土工程勘察报告，该边坡于18日当天发生了滑坡，验证了本文的分析结果。

6 结论

(1)建立了降雨条件下基于云模型的建筑边坡稳定性评价体系，并根据评价体系对不同降雨情况下的边坡稳定性进行评价，获得了边坡基本稳定—欠稳定以及欠稳定—不稳定的降雨阈值方程。

(2)采用本文方法对福建省南平市金龙花园小区边坡在当地强降雨期间，即2010年6月13至18日的稳定性评价结果表明，其中5天的评价结果与实际情况吻合，包括准确预测了6月18日会发生滑坡。只有6月15日的评价结果与实际情况有偏差，其原因是评价中对当日降雨历时取值24 h，而实际的降雨历时应该没有24 h。因此，当对降雨条件掌握较为准确的情况下，本文方法对边坡稳定状态的评价结果具有较高的可靠性。

(3)由于各个建筑边坡的特征参数不一，目前还没有任何一种方法能够适用于所有边坡在降雨条件下的稳定性评价。该方法适应于某一时间内连续降雨对边坡稳定性的持续削弱作用，尚未考虑边坡稳定性恢复的情况。文中建立的降雨阈值方程是针对某一具体边坡的，其他类似边坡可参照本文的方法推导出类似的降雨阈值方程进行评价。