汽车转向系统双十字轴万向节式中间轴受力分析

潘乙山 李 晗

(博世华域转向系统有限公司,上海 201801)

0 引言

双十字轴式万向节从首次被用在汽车上至今已有一百多年，由于其构简单而被广泛用于汽车转向系统。十字轴式万向节的不等速特性由法国工程师Jean Victor Poncelet用球面三角公式首次证明，十字轴式万向节在转动过程中，节叉会同时受到扭矩和弯矩的作用[1-2]。汽车转向系统上的中间轴安装在转向机和转向管柱之间，由于安装转向机的副车架和安装转向管柱的横梁，两者相对位置在汽车行驶过程中会产生微小变化，该变化导致中间轴产生伸缩运动，伸缩运动产生的轴向滑动力也会影响到中间轴的受力。转向系统中的多种噪音与中间轴的受力情况相关，如粘-滑尖叫声(Stick - Slip)、转向管柱周期性咯哒声等，所以在转向系统设计时对其进行正确受力分析至关重要。本文将扭矩、弯矩及滑动力三者同时在转向管柱坐标系中表示出来，以便于后续对转向管柱支撑轴承的受力情况进行分析。

1 中间轴受力分析

中间轴用于传递驱动单元的输出扭矩到机械转向机上。不同结构的中间轴所能承载的最大扭矩不同，如图1给出了ZF公司不同结构中间轴所能承受的最大扭矩范围[3]。注塑滑动结构的中间轴能传递的扭矩较小，而球滑动结构的中间轴能传递的扭矩较大。直线安装的中间轴仅能传递扭矩，无附加弯矩产生，带角度安装的中间轴在传递扭矩的同时会产生附加弯矩。为便于装配以及提供溃缩功能，中间轴一般都有伸缩功能，伸缩过程中会产生轴向滑动力。

图1 不同结构中间轴所能承受的最大扭矩(图片来源：参考文献3)

Fig.1 Transmission torque of each kind of intermediate shaft

1.1 中间轴的结构及原理

如图2所示，注塑滑动结构的中间轴由下摆动节叉1、下固定节叉2、花键轴3、花键套管4、上固定节叉5、上摆动节叉6等部分组成[4]。花键轴3与花键套管4之间由注塑滑动结构间隔开来，以降低滑动力；下摆动节叉1与下固定节叉2、上固定节叉5与上摆动节叉6分别用十字轴链接，十字轴与节叉之间有滚针轴承，用来降低摩擦损失。下摆动节叉的轴线与花键轴的轴线、上摆动节叉的轴线与花键管的轴线之间可以布置成不同的夹角，以满足转向系统的空间布及扭矩波动的要求。

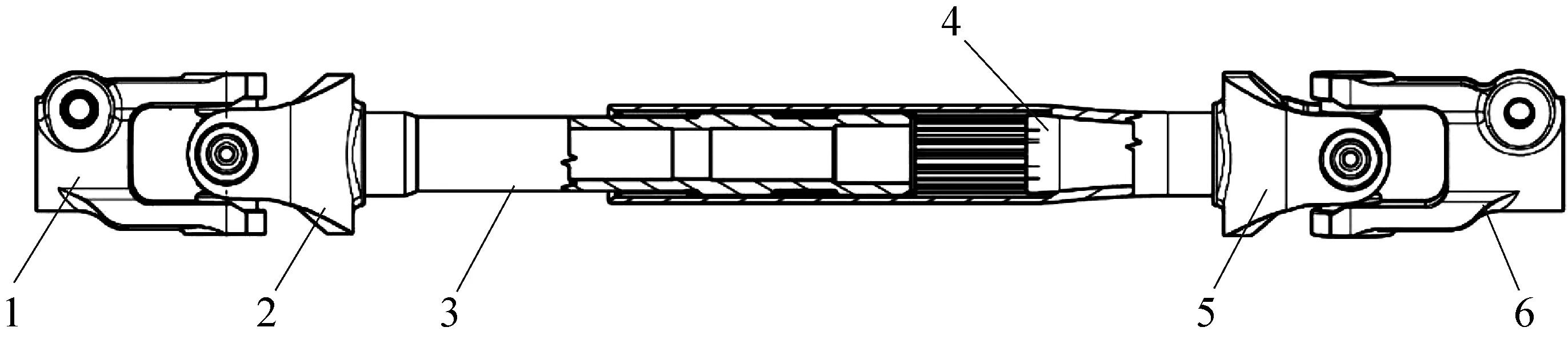
图2 博世华域转向系统有限公司中间轴(图片来源：参考文献4)

1.2 单十字轴万向节受力分析

1.2.1 特殊位置单十字轴万向节受力分析

如图3所示，节叉宽度为2h，单十字轴万向节带折弯角度传动时，主动节叉GI输入扭矩为T1，从动节叉GII输出扭矩为T2。由于万向节只能在其十字轴平面内传递力，图中表示为R，该力可分解成垂直于节叉轴线同时垂直于节叉平面的扭转力P和平行于节叉轴线及在节叉平面内的折弯力Z。输入扭矩和输出扭矩有以下关系[2]：

T1=2P1h

T2=2P2h

(1)

(a)

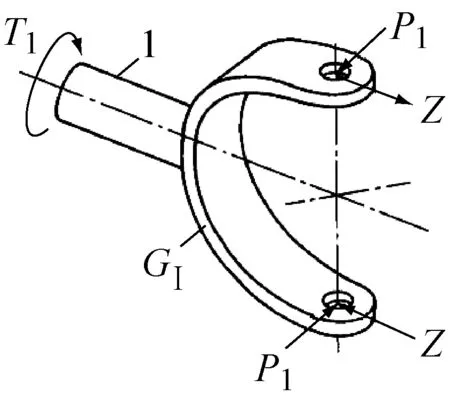
(b)

主动节叉所受的弯矩M1和从动节叉所受的弯矩M2分别为：

M1=2Z1h

M2=2Z2h

(2)

由于两个节叉的自身对称特性，结合图3可知，主动节叉GI和从动节叉GII旋转180°后又回到各自的初始状态，故十字轴万向节的扭转力P和折弯力Z的周期均为180°。

当主动节叉转动角度为0°和90°时，节叉的扭矩和弯矩见表1[2]：

从表1可知，节叉所受最大弯矩与十字轴万向节传递的扭矩大小、输入输出轴间夹角大小有关。若要对中间轴进行比较完整的受力分析，还需要知道节叉在任意位置时的受力状态。

表1 特殊位置节叉的扭矩和弯矩

1.2.2 单十字轴万向节状态变换

双十字轴万向节中间轴的参数设定如图4所示：

图4 中间轴模型参数

Fig.4 Parameters of intermediate shaft

先对其中的上万向节进行分析，如图5所示，上万向节的坐标系S定义如下：坐标原点B为十字轴中心点，X轴为主动节叉的轴线，Y轴为主动节叉耳轴线，Z轴为从动节叉耳轴线。输入轴线与输出轴线成夹角状态的万向节，可由输入轴线与输出轴线同轴状态的万向节，经过以下步骤得到：

1)将主动节叉轴线AB与从动节叉的轴线BC摆成同轴状态，主动节叉耳孔轴线Y1Y1与从动节叉耳孔轴线Y2Y2成垂直状态，主动节叉耳孔轴线Y1Y1在XY平面内；

2)将从动节叉绕其节叉耳孔轴线Y2Y2顺时针旋转β21角；

3)将主动节叉绕其轴线AB顺时针旋转φ1角；

4)将从动节叉绕其轴线BC顺时针旋转-φ2角，直到主动节叉耳孔轴线Y1Y1与从动节叉耳孔轴线Y2Y2垂直。

结合图3、图4和图5的参数设定并用向量形式表示，根据万向节变换步骤1，此时为初始状态，各向量在坐标系S上的表示见下表2。

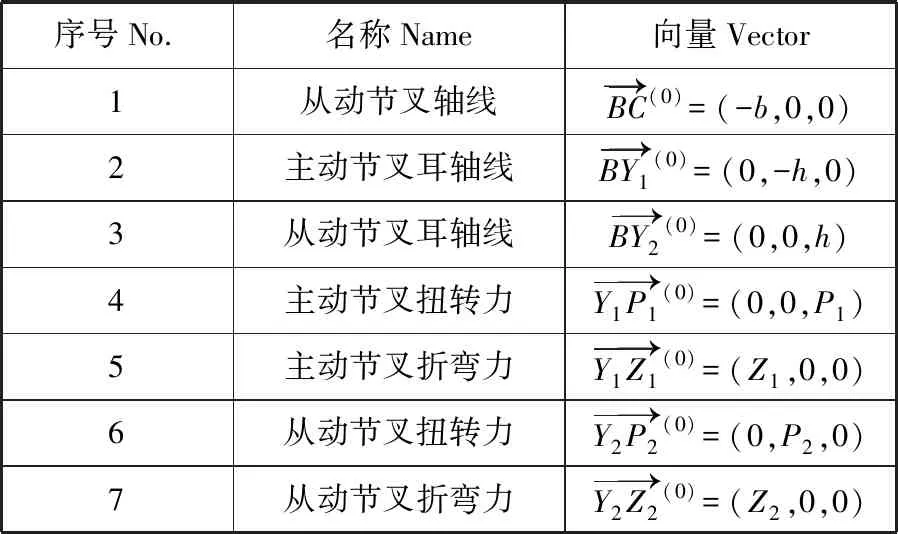
表2 初始状态向量表示

注：上标0表示向量的初始状态。

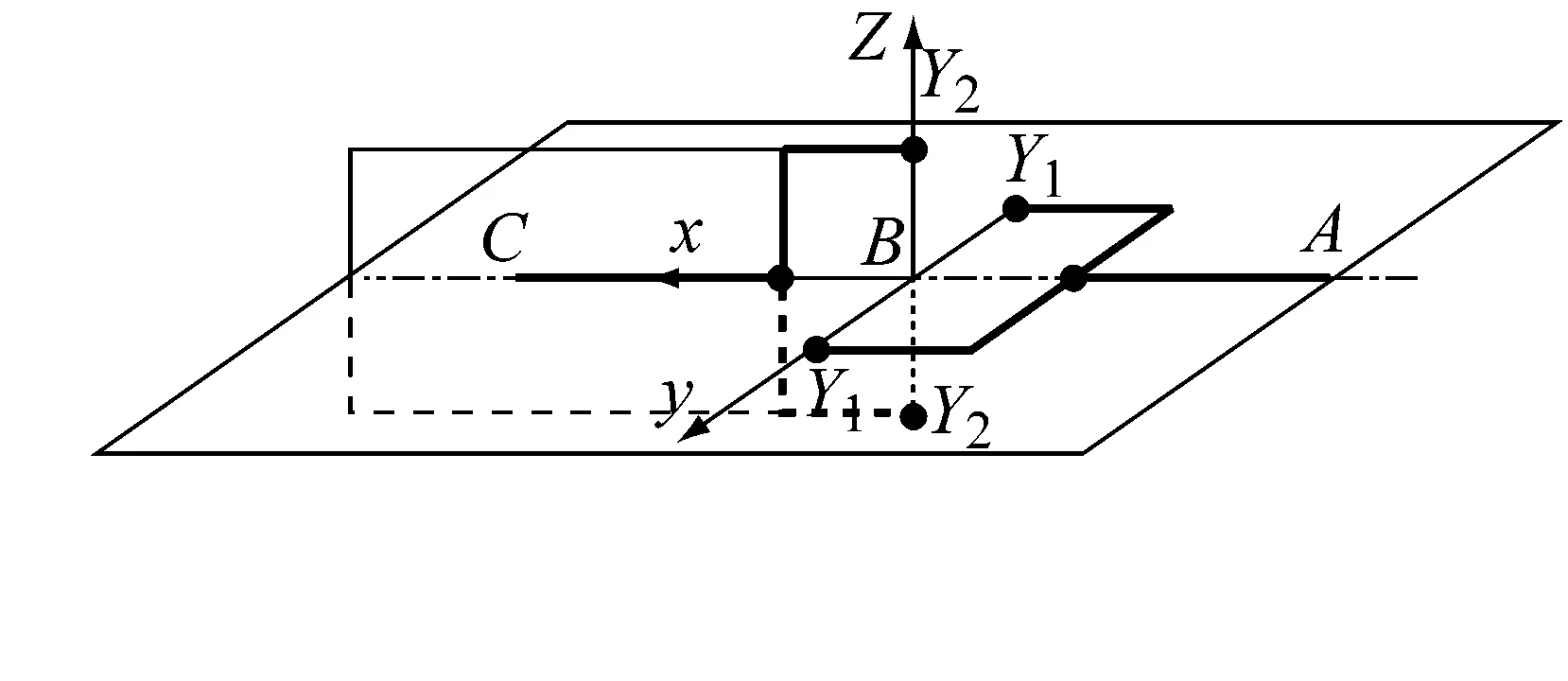
(a) 步骤1

(b) 步骤2

(c) 步骤3

(d) 步骤4

图5 十字轴万向节旋转过程

Fig.5 Transformation of U-joint

步骤2、步骤3和步骤4的变换矩阵[5]分别为：

为了方便书写，将坐标变换矩阵RBC简写成：

初始状态向量经过步骤2、步骤3和步骤4的变换后的结果见表3。

表3 变换后向量表示

1.2.3 单十字轴万向节受力平衡求解

cosβ21tanφ2=tanφ1

(3)

若以主动节叉耳孔轴线在主动轴和从动轴所成平面内为初始位置，称为同相或0°相关。若以主动节叉耳孔轴线在上述平面的垂直平面内为初始位置，称为正交90°相关[2、6]，并有以下关系：

cosβ21tan(φ2+90°)=tan(φ1+90°)

化简后有：

tanφ2=cosβ21tanφ1

(4)

(5)

正交时式(4)可写成：φ2=atan(cosβtanφ1) ，对式子连边对时间t求导：

(6)

不考虑内摩擦功率损失时，输入功率等于输出功率：

T1ω1=T2ω2

(7)

式(7)中，ω1为主动节叉角速度，ω2为从动节叉角速度：

(8)

由式(5)到式(8)，可解得同相时主动节叉扭矩T1与从动节叉扭矩T2满足以下关系：

(9)

正交时满足以下关系：

(10)

P1=P2cosβ21+Z2sinβ21cosφ2

(11)

正交时可解得：

P2=P1cosβ21+Z1sinβ21sinφ1

(12)

根据式(3)～(4)和(9)～(12)可化简可得同相节叉和正交节叉的弯力公式：

Z1=P1tanβ21sinφ1

Z2=P2tanβ21cosφ2

(13)

参考文献2中表1的特殊位置的扭矩及弯矩结果与式(1)～(2)、(9)～(10)、(13)计算的结果相符。

1.3 双十字轴结构中间轴弯矩与传递扭矩的关系

由于单万向节传动比不固定，一般会采用多个万向节组成特定角度布置的传动系统来实现等速传动。常见的等速双万向节传动系统有Z型布置和A型布置，图4所示的中间轴模型类似A型布置。根据多万向节等速传动原理[6]，可令输出节叉1为同相、上节叉2为正交、下节叉3为正交、小齿轮节叉4为同相。若定义扭矩正向传递为输出节叉1到小齿轮节叉4，则扭矩反向传递为小齿轮节叉4到输出节叉1。上一小节所得公式同时适用于双十字轴结构中间轴扭矩正向传递和扭矩反向传递情况。对于扭矩反向传递，由式(1)～(4)和(13)可得：

tanφ4=cosβ43tanφ3

tanφ1=cosβ21tanφ2

M4=T4tanβ2sinφ4

M3=T3tanβ2cosφ3

M2=T2tanβ1cosφ2

M1=T1tanβ1sinφ1

(14)

式(14)中，输出节叉1转角φ1、上节叉2转角φ2、下节叉3转角φ3、小齿轮节叉4转角φ4初始值均为0°，转角的变化范围均为0°～180°。两个万向节之间的中间连接轴的扭矩有：

T3=T2

(15)

在中间轴设计时，令上下万向节的相位角θ与上下万向节平面的夹角γ的差值尽量等于0°，可实现近似的等速传动。上节叉2转角与下节叉3转角，扭矩正向传递及扭矩反向传递时分别有以下关系：

φ3=φ2+γ-θ

φ2=φ3+γ-θ

(16)

以电动助力转向系统(EPS)为例，结合图6对EPS系统坐标系Sc做如下定义：坐标原点O为上万向节十字轴中心，X轴为上管柱轴线，Y轴垂直于上管柱轴线同时在水平面上，Z轴向上并垂直于转向管柱轴线。上万向节平面与EPS系统坐标系Sc的XY平面的夹角称为连接角δ，一般左舵车的中间轴连接角为正值，右舵车的中间轴连接角为负值。在坐标系Sc下，输出轴的转角φ的初始零位为Y轴的正方向，定义左打方向为正转，右打方向为反转。结合公式(14)中输出节叉1转角φ1的定义，可知输出节叉1转角φ1超前输出轴的转角φ的角度为连接角δ：

φ=φ1-δ

(17)

作用在节叉上的力偶矩，定义其使节叉产生绕Z轴折弯的分量为竖直轴弯矩，使节叉产生绕Y轴折弯的分量为水平轴弯矩。则输出节叉1上的弯矩M1可分解成竖直轴弯矩M1z和水平轴弯矩M1y：

M1z=M1cosφ=M1cos(φ1-δ)

M1y=M1sinφ=M1sin(φ1-δ)

(18)

1.4 双十字轴结构中间轴滑动力与传递扭矩的关系

EPS系统安装在整车上时，机械转向机安装在副车架上，上转向管柱安装在横梁上。在汽车行驶并有转向运动的过程中，由于有路面颠簸冲击，中间轴上万向节中心点到下万向节中心点的距离会产生变化，根据整车CAE分析，一般该距离变化幅度会在±2 mm内[7]。若双十字轴结构中间轴在传递扭矩的时候产生轴向滑动，将会产生轴向滑动力Fi(仅考虑中间轴伸缩过程产生的稳定滑动力，不考虑静动摩擦力转变的突变力)。中间轴拉伸时Fi为负，中间轴压缩时Fi为正。该滑动力近似的正比于中间轴传递的扭矩T2：

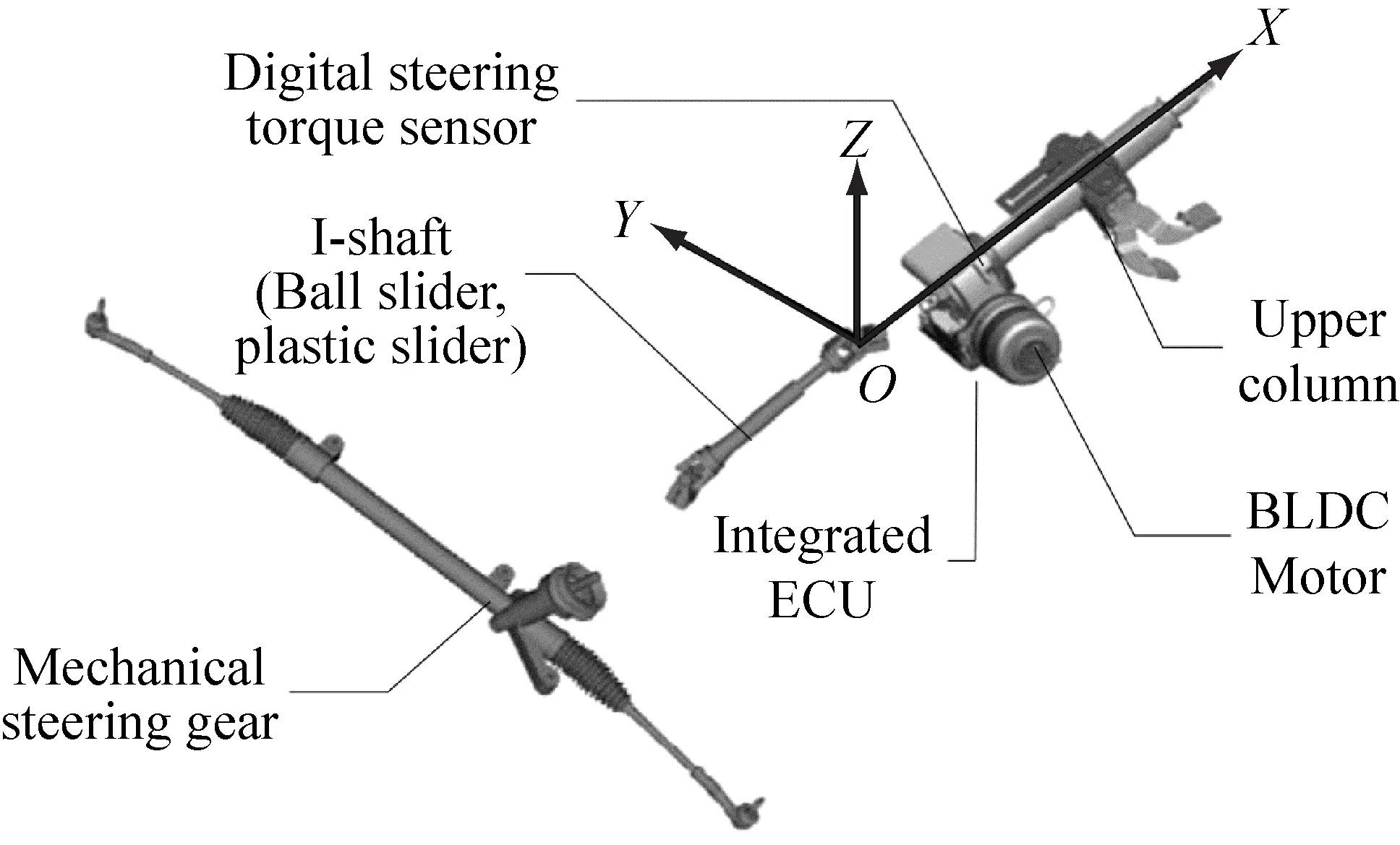
图6 EPSc系统坐标系Sc定义(图片来源：参考文献3)

Fi=kT2+F0

(19)

上式中，k为中间轴滑动力系数，F0为中间轴初始滑动力。一般的，注塑滑动结构的中间轴滑动力系数k≈10，中间轴初始滑动力F0约为20 N；球滑动结构的中间轴滑动力系数k≈4，中间轴初始滑动力F0约为10 N。在坐标系Sc下，对于左舵的中间轴，中间轴的轴向滑动力、水平滑动力、竖直滑动力分别为：

Fix=Ficosβ21

Fiy=Fisinβ21cosδ

Fiz=Fisinβ21sinδ

(20)

2 中间轴受力分析实例

下面以左舵的注塑滑动结构中间轴为例，假设施加在小齿轮轴节叉上的扭矩T4=90 Nm，小齿轮轴以ω4的转速匀速转动。用上述公式对其进行受力分析，并已知硬点参数如下表4：

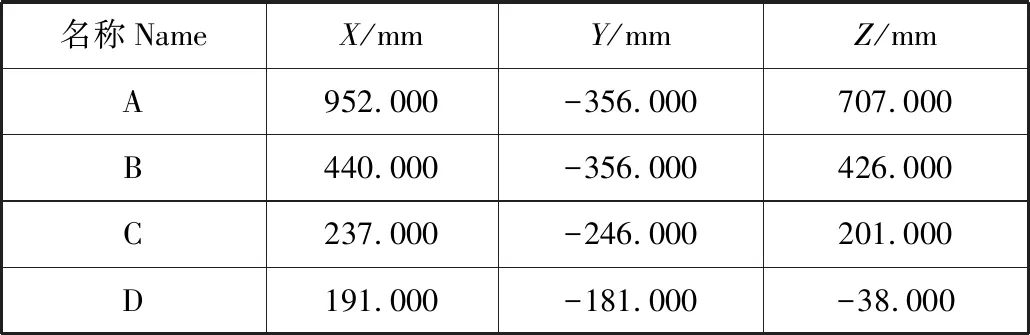
表4 中间轴硬点参数

根据上表4的中间轴硬点参数计算可得：

表5 中间轴计算结果

上下万向节平面的夹角γ为48.965°。相位角由于装配原因，会产生大约±5°的公差。若EPS的转向管柱带有位置调节功能，中间轴硬点参数也会随着调节位置不同而产生变化，本计算不考虑这种变化状态下的受力。小齿轮节叉4转角φ4匀速转动，可得到不同位置节叉的转角随时间变化的曲线及扭矩随小齿轮节叉4转角φ4变化的曲线：

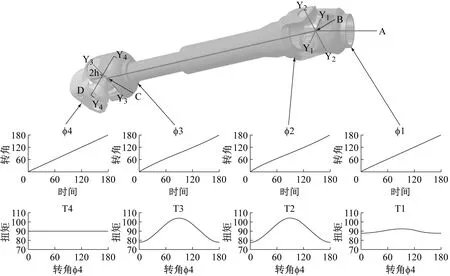
图7 不同位置节叉的转角曲线和扭矩曲线

Fig.7 Rotate angle and transmission torque of each fork

从图7可见，给输入节叉一个匀速转动速度，中间两个节叉转速不均匀，而最后的输出节叉转角已经基本能实现匀速转动。给输入节叉一个固定扭矩，中间两个节叉扭矩不均匀，而最后的输出节叉的扭矩已经基本能实现比较平稳的扭矩输出。

图8是方向盘正转和反转时中间轴给转向管柱的弯矩示意图。

(a) 方向盘正转

(b) 方向盘反转

图8 转向管柱输出轴的弯矩

Fig.8 Bending torque on output shaft of steering column

上图是沿着坐标系Sc的X轴反方向看过去所得图，图中的虚直线平面即上万向节平面，带箭头虚弧线指的是旋转方向，带箭头的虚直线指的是弯矩最大的方向，此时节叉耳轴线Y1Y1与上万向节平面垂直。方向盘每转动一周，最大值出现两次。

图9是中间轴伸缩运动对转向管柱产生的沿坐标系Sc三个方向的分力。

图9 中间轴最大分力

实际上由于整车振动的随机性，沿坐标系Sc三个方向的分力在某个中间轴转角下，取值可正可负，上图只是其取值为正时的最大包络，反应出该位置可能出现的最大值。该最大值可用于转向管柱支撑轴承的寿命计算。

3 结论

本文通过向量的坐标变换计算，推导出十字轴万向节转角公式、十字轴万向节扭矩及弯矩公式，最终得到中间轴施加在转向管柱上的扭矩及弯矩曲线，并分析了其受力特点。由于转向系统的转速较低，准静态平衡受力分析基本能满足需求，扭矩及弯矩曲线可用于指导转向管柱支撑轴承的噪音分析及寿命计算。