基于陷波器的LCL型并网逆变器的谐振特性
2020-05-08常国祥吴振鑫
常国祥, 吴振鑫
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
在大功率光伏并网中使用L滤波方式,需要较大的滤波电感,增加了系统的体积,损耗和成本,也增加了控制系统惯性从而降低电流内环的响应速度。而LCL型逆变器在同样谐波标准和开关频率时,可以采用较小的滤波电感设计,所以LCL型滤波方式被广泛应用在大功率光伏并网发电中。但其存在谐振问题,极大地影响了系统的稳定性和并网的效果,所以解决LCL型逆变器的谐振问题有着重要的意义。谐振问题是由于系统的阻尼太小造成的,而增加系统阻尼的方法有无源阻尼法和有源阻尼法。无源阻尼会使系统增加额外的损耗并影响滤波效果,而有源阻尼是通过算法来增加阻尼不存在上面的问题,所以被广泛接受和利用[1-3]。
肖华锋等[4]总结了几种虚拟电阻法,并对其进行了分析,但是受控制器结构及控制宽带的局限,效果并不是很好。应用状态反馈可以对闭环控制系统进行任意极点的配置,如赵磊等[5]提出了线性二次型(LQ)法。Dannehl等[6]提出的直接极点配置法,这些设计很大程度上依赖设计者的经验。许津铭等[7]分析了不同状态变量加权组合的情形,发现电流之间的加权值均为比例系数,而电流电压之间加权和电压之间加权的权值会用到积分或者微分,故常用电流加权平均的方法,但由于反馈量不是并网电流,需要加必要的补偿才能实现单位功率因数,这样就增加了控制系统的复杂性。卞文倩等[8]提出构造一个具有负谐振峰特性的环节来消除正谐振峰值,其不仅容易理解,构造方便而且消除谐振的效果很好,对系统的高频及低特性均无影响。文献[9-10]提出虚拟磁链定向的控制方法能消除电网电压中谐波对并网的影响,降低系统出现震荡的概率。笔者以VFOC控制策略为基础,在电网电流为反馈量的前向通道中引入以电容电流为反馈量的反馈回路,并把该反馈回路配置成能产生负谐振峰的传递函数,用来抵消LCL滤波器产生的正谐振峰值,在Matlab中对新构造的数学模型进行效果验证。
1 系统建模
1.1 LCL型逆变电路
三相三电平LCL型逆变器的电路拓扑如图1所示。其中DC1与DC2为直流侧电压;ua、ub、uc分别为abc三相逆变侧的相电压;La、Lb、Lc分别为abc三相逆变侧的滤波电感;Lga、Lgb、Lgc分别为abc三相电网侧的滤波电感;Ca、Cb、Cc分别为abc三相电网侧的滤波电容和等效电容之和;iL、iC、iLg分别表示通过逆变侧电感的电流,通过滤波电容的电流,通过网侧电感的电流;Ea、Eb、Ec分别为abc三相的电网电压;Sa1~Sa4、Sb1~Sb4、Sc1~Sc4为开关管和与其反并联的二极管;D1~D6表示拑位二极管;O为三电平的中点(假设中点电位平衡)。
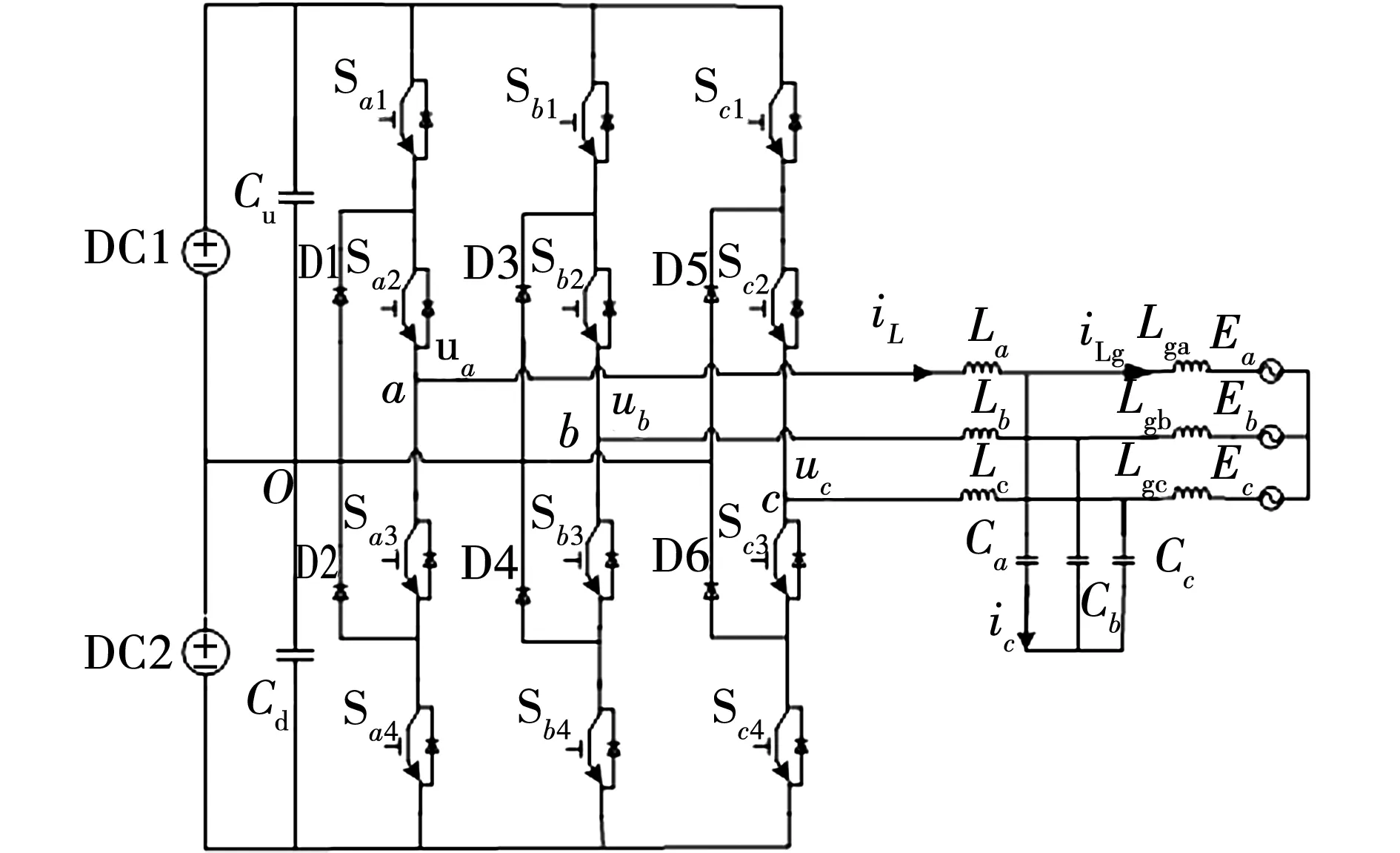
图1 三相三电平LCL型逆变电路Fig. 1 Three phase three-level LCL inverter circuit
1.2 电路等效模型
对图1的硬件电路进行数学描述,其电路等效模型如图2所示,图中,Ginv(s)是调制波到逆变器输出电压的传递函数,以ab两相作为一个回路来进行分析且ua>ub(以下讨论均是如此)。

图2 电路等效模型Fig. 2 Circuit equivalent model
式中:Udc——逆变器的等效增益;
Ts——电流内环采用周期;
ZL(s)、ZC(s)、ZLg(s)——(La+Lb)、(Ca+Cb)、(Lga+Lgb)的阻抗,且有ZL(s)=ZLa(s)+ZLb(s)=sLa+sLb=sL;ZC(s)=ZCa(s)+ZCb(s)=1/sCa+1/sCb=1/sC;ZLg(s)=ZLga(s)+ZLgb(s)=1/sLga+1/sLgb=1/sLg;
Eg——电网侧的电压,且Eg=Ea+Eb。
在图2的基础上,将Uc(s)后面的引出点后移到ILg(s)处,再将IL(s)后面的比较点前移到Uab(s)后面,得等效模型如图3所示。为了更好地对LCL进行分析,将LCL滤波结构进行整合后可得其简化等效模型如图4所示。
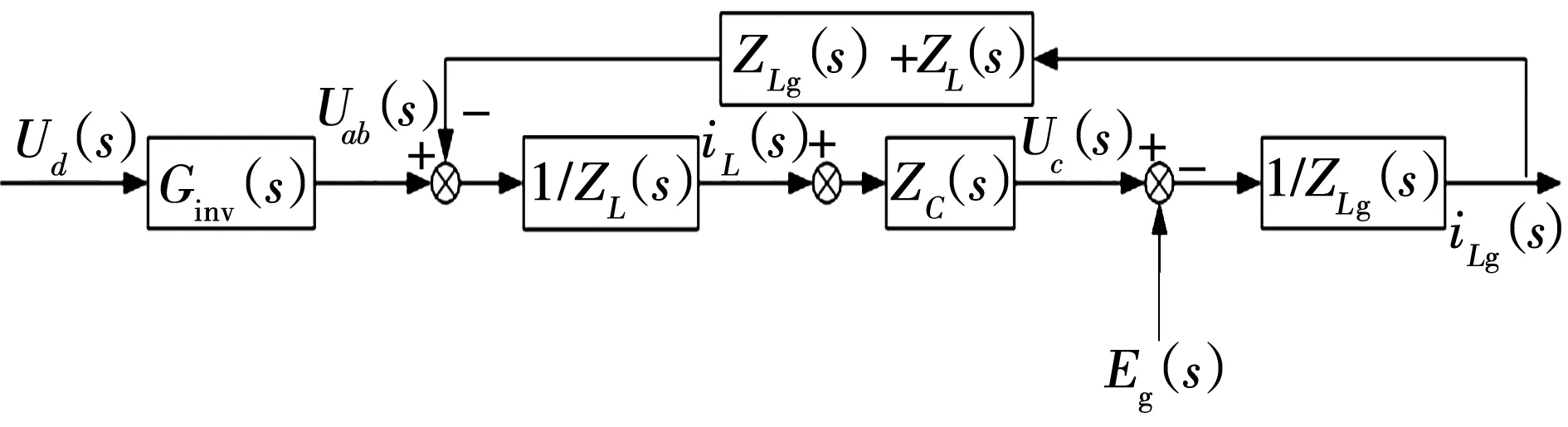
图3 等效模型框Fig. 3 Equivalent model block
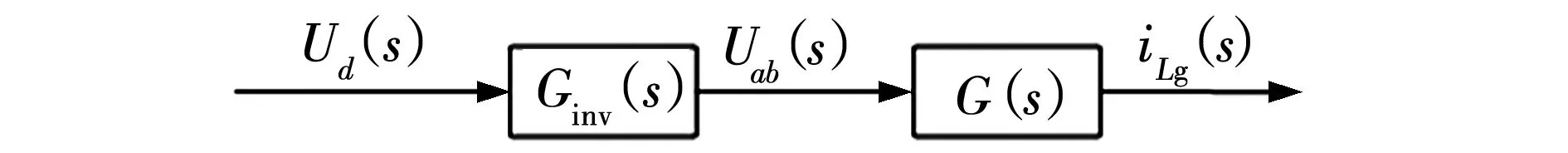
图4 等效模型化简Fig. 4 Simplified of equivalent modeling
图中,Ud(s)为逆变器直流侧调制波的电压;Uab(s)为逆变侧输出电压;G(s)为LCL型滤波结构的传递函数
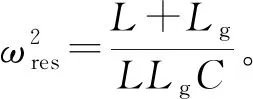
显然,由传递函数可知该系统存在一个正的谐振点。
2 陷波器的构造
2.1 VFOC的基本原理
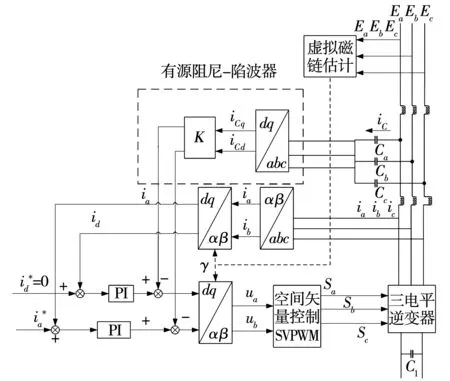
图5 以iC为反馈量的基于陷波器校正的有源阻尼控制Fig. 5 Active damping control block based on Notch correction with iCas feedback
(1)
(2)
Xqd=TpXβα,
(3)
(4)
2.2 带陷波器的系统
在电网电流环前向通路中构造陷波器,其构造原理如图6所示。图6中E(s)为逆变器侧输出电压Uab到所选的反馈变量处的传递函数;K(s)为选取不同反馈量时配置的传递函数。
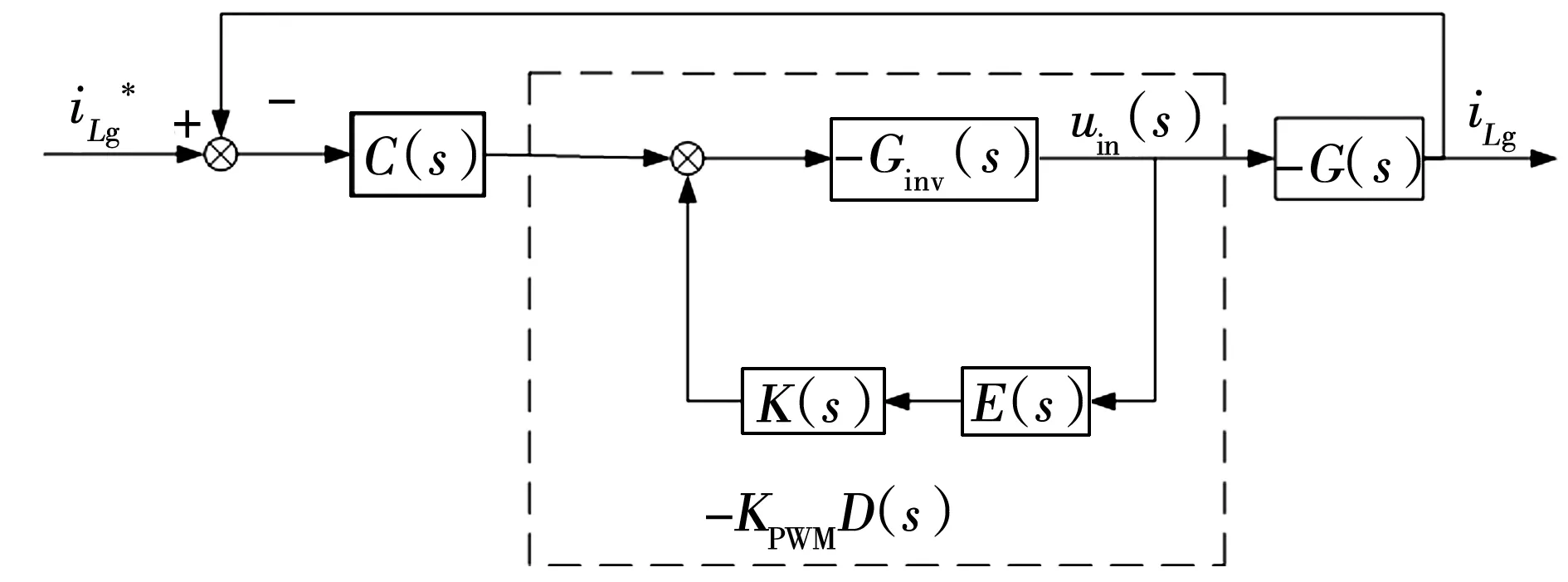
图6 陷波器结构有源阻尼算法结构Fig. 6 Structure of active damping algorithm for notch filter structure
文中所引入的陷波器传递函数为
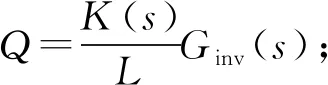
C(s)——并网电流调节器的传递函数,C(s)=Wc(s)Wf(s);

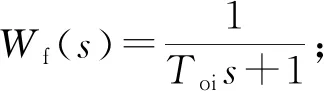
τ——积分时间常数,τ=L/RL;
toi——电流反馈滤波时间常数;
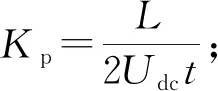
t——开关管导通时间。

通过在电流环前向通道中引入合适的反馈变量,并使其与该电流环的前向通道构成闭环系统,然后对其进行合理的配置,使其具有陷波器的特性,从而实现对LCL并网逆变器的有源阻尼控制。但是选取反馈量的不同会导致系统在配置陷波器的传递函数时存在差异[11]。就LCL型并网逆变器而言,在电网侧电流为主回路的情况下,反馈量的选择可能有以下5种情况:电网侧电感电压u2,滤波侧电容电压uC,滤波侧电容电流iC,逆变器侧电感电压u1,逆变器侧电感电流iL。当选取滤波侧电容电流为反馈量时只需要将陷波器中的K(s)配置成比例环节;但选取电网侧电感电压和滤波侧电容电压作为反馈变量时,需要将陷波器中的K(s)配置成微分环节;选取逆变器侧电感电压与逆变器侧电感电流当反馈时,在配置K(s)将更为复杂。所以文中选取了实现起来较容易而且不受系统其它参数影响的滤波侧电容电流作为反馈量。选取不同反馈量时的E(s)为
代入具体系统参数值后E(s)和其对应的K(s)为:
3 系统参数
为了尽可能的减少无功功率,一般在选择电容大小时限制其产生的无功小于系统额定功率的5%,应该满足式(5),其中Pn为并网逆变器额定功率,UC为滤波电容电压,Un为并网逆变器额定电压且有UC=Un。
(5)
从稳态条件下并网逆变器输出功率的能力考虑,对并网逆变器LCL滤波器的总电感量应给予合理的限制。若采用SVPWM控制策略,其应该满足关系为
(6)
式中:Ep——网侧电压的峰值;
ILP——滤波电流的峰值;
Udc——直流侧电压。
首先确定的是逆变桥测的电感值,为尽可能的降低开关损耗,保证开关管在承受的开关应力范围内,需要考虑逆变桥侧电流纹波对电感选择的影响。逆变器侧的电感值与最大电流纹波幅值应满足关系式为
(7)
式中,Δi——最大电流纹波幅值。
在初选并网逆变桥侧的电感后,由式(6)与式(8)联合可以确定网侧电感值。
(8)
式中:hsw——开关谐波次数,hsw=ωsw/ωn,一般约为20%;
wsw——开关谐波的频率;
ωn——开关角频率;
γ——网侧电感与逆变桥侧电感值之比;
x——滤波电容吸收系统功率中无功功率的百分比,且有x≪5%;
Cb——电容单位值。
文中的谐振频率设计应满足公式
10fn≪fres≪0.5fsw。
文中选取逆变器的开关频率fsw=10 kHz;逆变器直流侧电压Udc= 622 V;电网频率fo=50 Hz;电网电压有效值E=220 V。通过谐振公式计算可得,产生谐振频率fres=522 Hz;截止频率fc=2.19 kHz;滤波电容反馈系数K=3。
4 稳定性验证
图7为系统加入陷波器前后的Bode 图对比,其中红线表示无陷波器时的系统Bode图,绿色表示陷波器的Bode图,蓝色表示加入陷波器后的系统Bode图。对比之后,可以很清楚看出陷波器的谐振与LCL滤波器产生的谐振相位相同幅值相反,加入陷波器后的LCL型逆变器无谐振峰值;系统低频和高频开环增益受到陷波器的影响可以忽略不计,说明陷波器的引入并没有破坏LCL滤波环节对高频信号的抑制;从相位图中可见,原系统中由 LCL环节引入的共轭极点所引发的谐振频率处 180°相位突变也得到了改善。
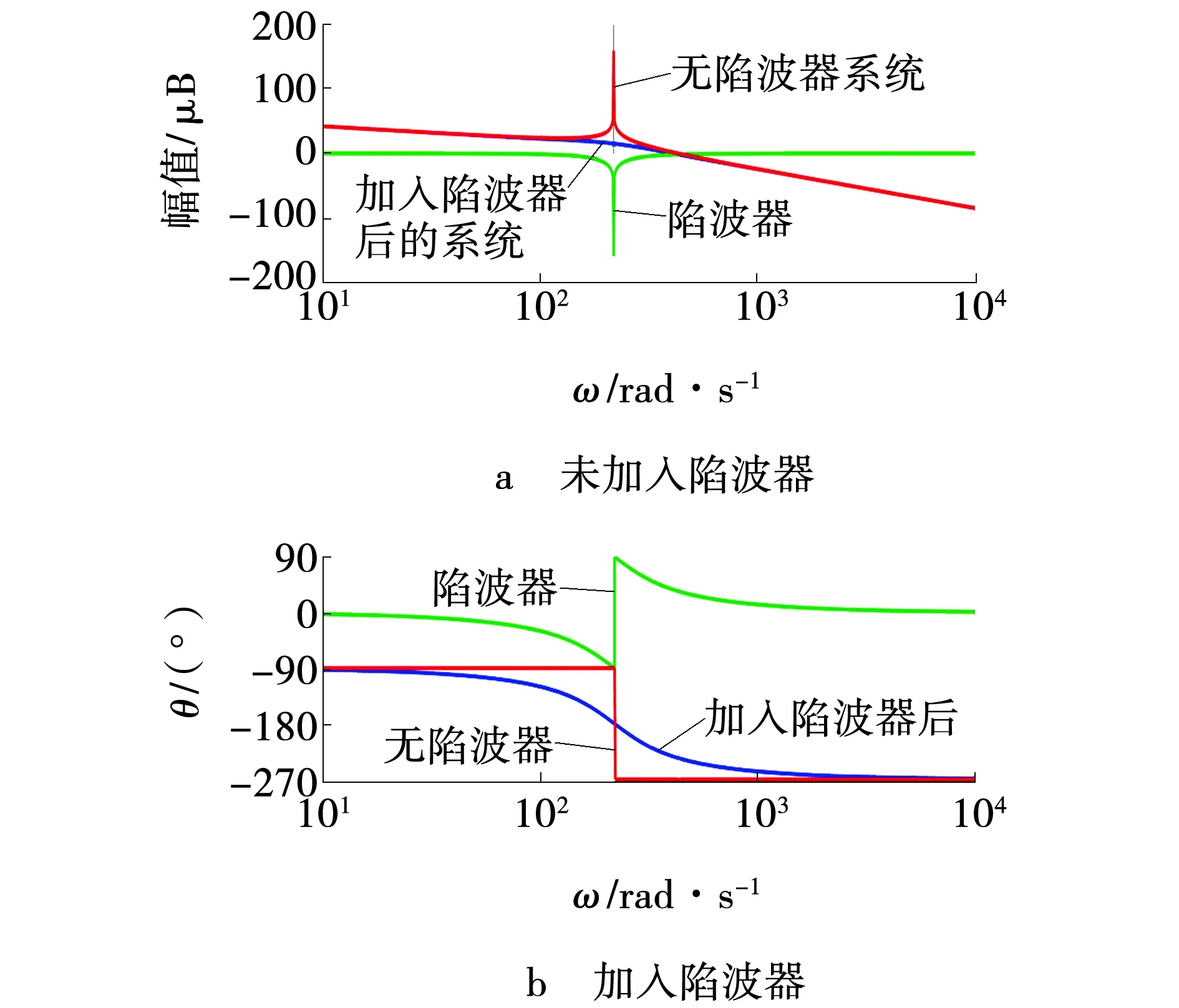
图7 加入陷波器前后的系统Bode图 Fig. 7 Bode diagram of system before and after adding notch filter
加入陷波器并以iC为反馈量构成有源阻尼控制器之后,文中对该系统的稳定性能进行了分析。图8为加入陷波器后的零极点图。图9为并网波形仿真图。
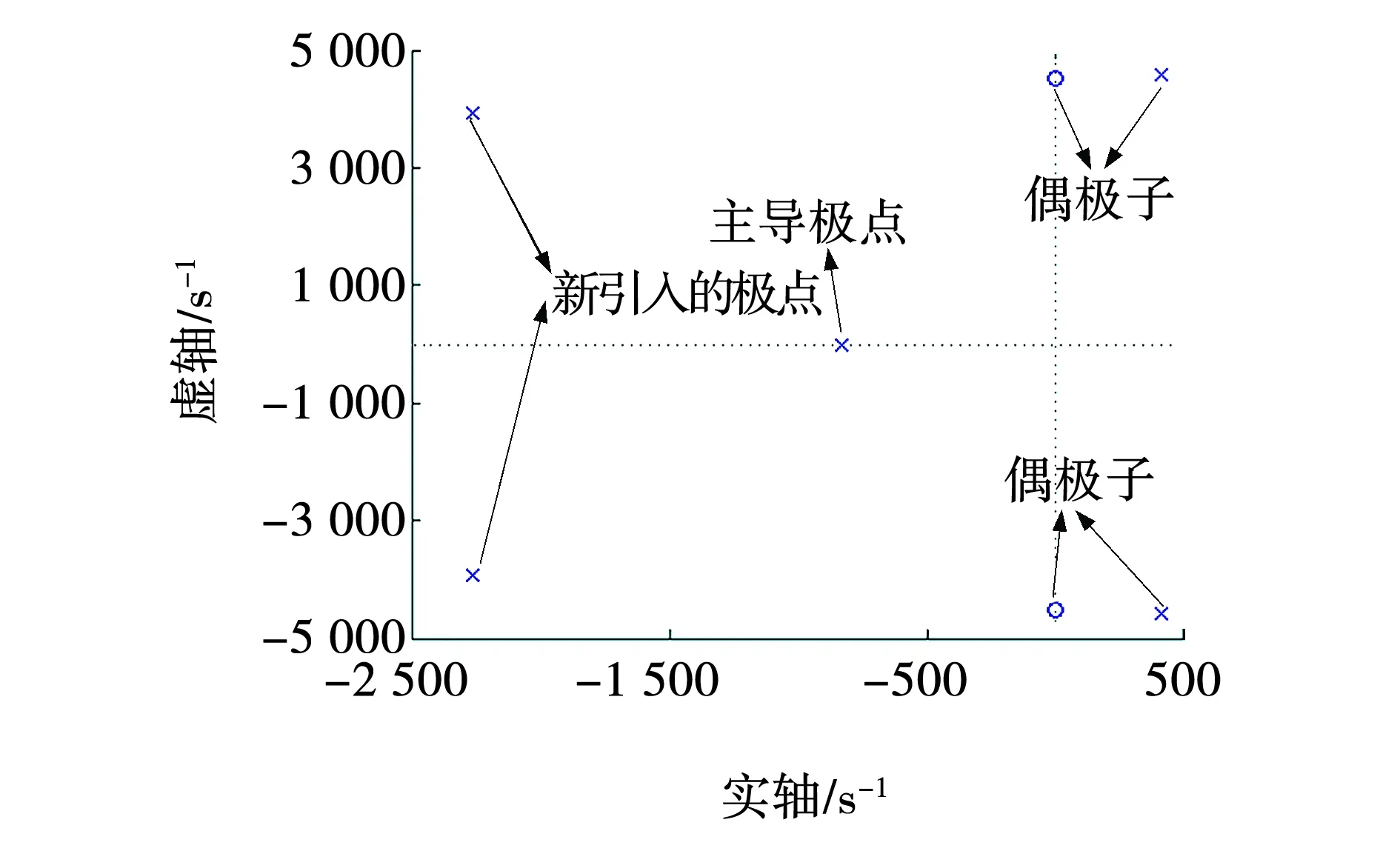
图8 加入陷波器后的零极点Fig. 8 Pole zero graph with notch filter
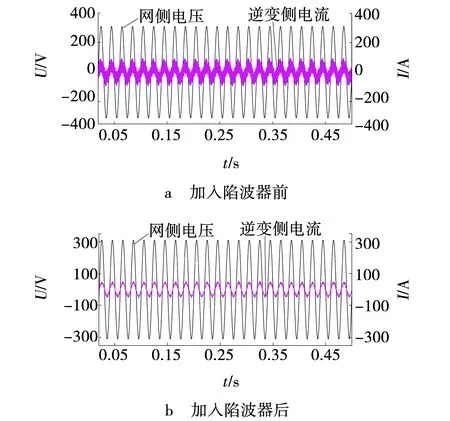
图9 并网波形Fig. 9 Grid connected waveform
由图8可知,未加入陷波器时,一对共轭主导极点位于虚轴右半平面,系统并不稳定;加入陷波器后,原来不稳定的主导极点与陷波器引入的一对零点构成偶极子消除了系统的不稳定性,而新引进的一对极点在负实轴区域,且离虚轴较远,所以对系统的性能无太大的影响。图9a为未加入陷波器时,并网系统在Simulink中的仿真波形,图9b为加入陷波器并以iC为反馈量构成有源阻尼控制器之后,并网系统在Simulink中的仿真波形。通过比对图9a和9b可知,加入陷波器并以iC为反馈量构成有源阻尼控制器之后,并网电流波形更加平滑,正弦效果更好且无谐振情况发生,增强了系统的稳定性和鲁棒性。
5 结束语
通过研究LCL型并网逆变器的谐振,对其建立了数学建模与稳定性分析,由LCL型并网逆变器的数学模型可知,其存在一个明显的正谐振峰值,加入陷波器,并在单电流控制环的基础上加入电容电流内环构成有源阻尼控制器,对其进行合理配置后,能够产生一个与系统正谐振峰值相位相同,幅值大小差不多但方向相反的负的谐振峰值。在Simulink中仿真分析了10 kW的并网系统,从示波器中可以看出,系统并网效果良好,谐波含量低,提高了整个系统的静态稳定性和鲁棒性。
