W断陷沉火山角砾岩致密气储层定量解释的方法

宋延杰， 陈仁杰， 唐晓敏， 孙 红， 权新荣

(1.东北石油大学 地球科学学院， 黑龙江 大庆 163318； 2.非常规油气成藏与开发省部共建国家重点实验室培育基地， 黑龙江 大庆 163318； 3.吉林油田研究院，吉林 松原 138000)

0 引 言

W断陷发育有侏罗系(J)和白垩系(K)两套沉积地层，下断上坳，西陡东缓。其中，S1段发育一套安山质沉火山角砾岩，埋深2 500～3 000 m，储层孔隙度分布范围在3%～12%之间，平均孔隙度为7.5%，空气渗透率分布范围在0.01～1.00 mD之间，平均渗透率为0.14 mD，属于致密火山岩储层[1]。国内外研究人员针对致密火山岩储层测井解释方法已经做了大量研究工作，在物性参数计算方面，提出了声波时差拟合、三孔隙度组合和中子、密度、声波测井值多元回归以及变骨架参数等方法计算致密火山岩基质孔隙度、裂缝孔隙度[2-6]；在孔隙度模型建立的基础上，通常利用孔隙度回归建立了火山岩储层渗透率模型[3-4,6-7]。

在火山岩含水饱和度计算方面，基于火山岩岩电规律和导电机理研究，建立了多种火山岩电阻率模型，如变m、n值的阿尔奇方程、基于孔隙-裂缝双重介质导电的电阻率模型、基于Maxwell导电模型和Fricke方程的改进电阻率模型、孔隙几何形态电阻率模型等[8-13]。但是，这些导电模型在描述火山岩孔隙结构变化对岩石导电规律影响方面还存在一定的不足，需要进一步研究。B.Z.Shang[14-15]提出了等效岩石元素模型，将岩石的孔隙空间分为对导电性影响大的小孔隙与影响小的大孔隙两部分，其中，小孔隙中电荷迁移效率高；大孔隙中电荷迁移效率低，通过引入孔隙结构效率参数描述小孔隙与大孔隙的体积比对岩石导电性的影响，有效提高了复杂储层饱和度解释精度。在此基础上，研究人员对等效岩石元素导电模型进行了一定的改进，并将其应用于孔隙结构复杂的致密砂岩、砂砾岩储层饱和度计算，取得了较好的效果[16-17]。目前，等效岩石元素导电模型研究仅仅针对砂岩、砂砾岩储层，而未开展过其对火山岩储层适用性的研究。

针对安山质沉火山角砾岩致密气储层物性差、孔隙结构复杂、微孔隙发育的特征，笔者给出了适应于安山质沉火山角砾岩致密气储层的孔隙度、渗透率、束缚水饱和度模型，并将描述复杂孔隙结构特征的等效岩石元素导电模型首次应用到安山质沉火山角砾岩储层饱和度解释。

1 储层孔隙结构特征

岩石薄片的分析表明，安山质沉火山角砾岩储层中发育孔隙和裂缝两种储集空间类型，孔隙型储集空间以微孔隙(图1a)和缩小粒间孔、粒内溶蚀孔(图1b)为主，它们在岩石中分布不均匀，连通性较差。裂缝型储集空间主要为构造缝以及微裂缝(图1c)，部分构造缝被方解石、黄铁矿、绿泥石等不同程度充填，而另有部分裂缝则被溶蚀扩大，致使储层孔隙结构复杂。

图1 储层微观孔隙结构类型Fig. 1 Microscopic pore structure types of reservoirs

基于压汞和核磁实验分析数据，根据岩石微观孔隙结构好坏，将安山质沉火山角砾岩储层划分为3类储层。I类储层排驱压力小于2 MPa，P25压力小于5 MPa，核磁T2弛豫时间大于10 ms的T2谱面积大，可动流体含量占比大，孔隙度大于8%，微孔隙体积百分含量平均为60%；II类储层排驱压力介于2～20 MPa，P25压力介于5～30 MPa，核磁T2弛豫时间大于10 ms的T2谱面积小，可动流体含量占比小，孔隙度介于5%～8%，微孔隙体积百分含量平均为80%；III类储层排驱压力大于20 MPa，P25压力达到65 MPa，核磁T2谱呈单峰结构，分布在T2弛豫时间10 ms以内，孔隙度小于5%，微孔隙体积百分含量平均为90%，见图2。综上所述，安山质沉火山角砾岩微孔隙发育、喉道细、渗透性较差。

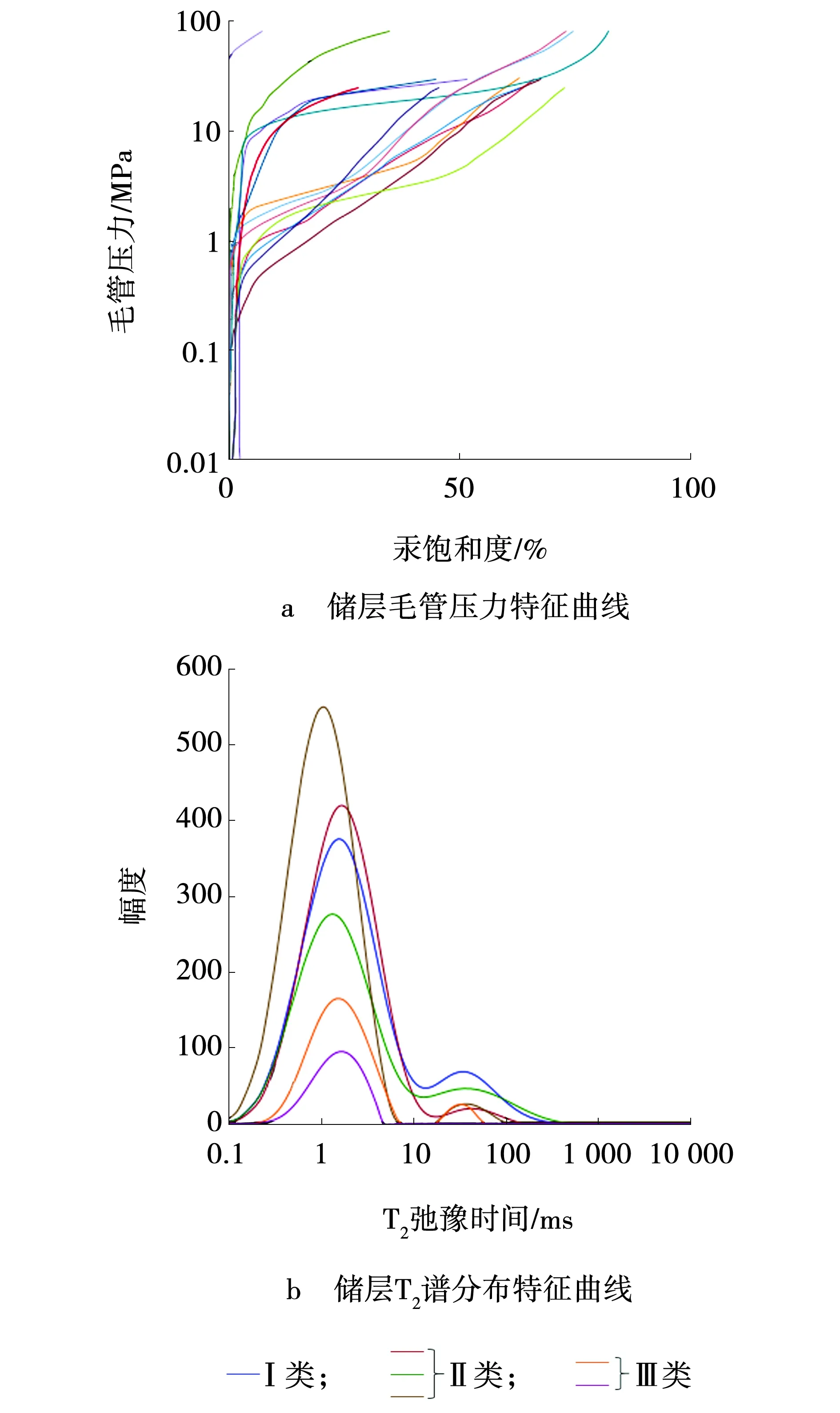
图2 安山质沉火山角砾岩储层特征Fig. 2 Tight andesitic volcanic breccia reservoir characteristics

2 储层参数测井解释模型的建立

2.1 孔隙度测井解释模型

W断陷安山质沉火山角砾岩骨架参数与常规砂岩、砂砾岩不同。利用岩心分析孔隙度及测井数据确定了安山质沉火山角砾岩的骨架参数，进而给出了孔隙度计算方法。

2.1.1 岩石骨架参数的确定

当致密储层岩性相同、流体类型一致时，随孔隙度减小，密度测井值和电阻率测井值均增大，中子孔隙度和声波时差测井值均减小，且当孔隙度趋近于0，岩石电阻率趋于无穷大时，储层的密度、中子孔隙度、声波时差测井值即为该种岩性的骨架密度、中子孔隙度、声波时差值。图3、图4分别给出了安山质沉火山角砾岩储层(去掉明显含气层以及井眼扩大明显层)岩心分析孔隙度(φc)与密度测井值(ρd)以及电阻率测井值(ρRT)与密度测井值的交会图，从图中可以看出，岩心分析孔隙度与密度测井值关系较好，当孔隙度为0，电阻率趋于无穷时，对应的坐标值为2.67 g/cm3，即安山质沉火山角砾岩骨架密度值近似为2.67 g/cm3，同理，确定了中子孔隙度、声波时差值为0.08、174 μs/m。

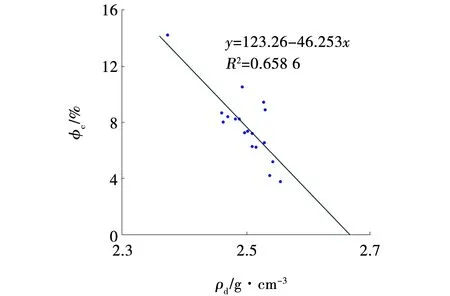
图3 密度测井值和岩心分析孔隙度交会Fig. 3 Cross plot between density log and core analysis porosity

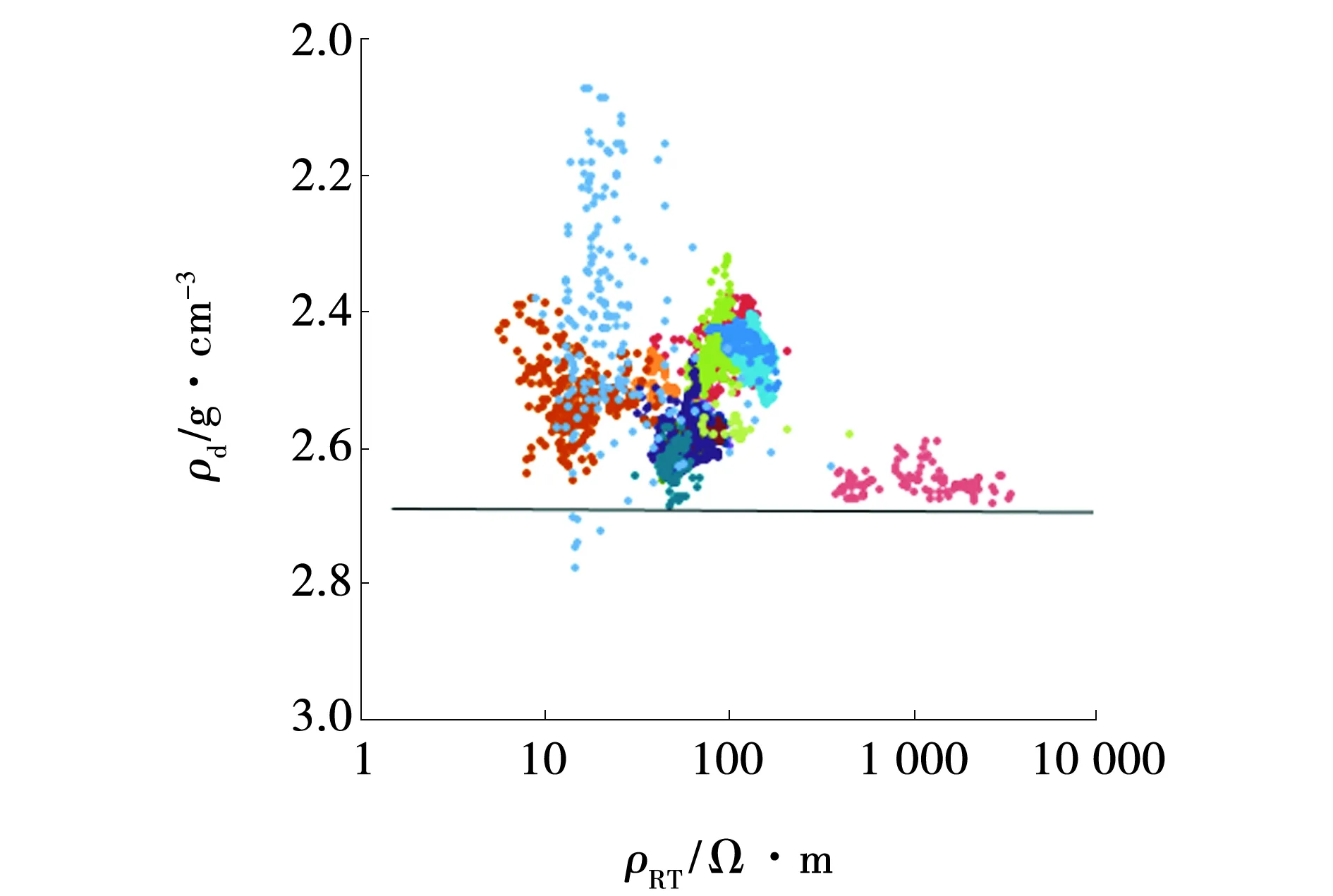
图4 密度测井值和电阻率测井值交会Fig. 4 Cross plot between density log and resistivity log

2.1.2 孔隙度计算模型

储层含气使中子孔隙度减小，密度孔隙度和声波孔隙度增大。考虑储层含气性影响，利用5口井18块安山质沉火山角砾岩岩样的中子孔隙度和密度孔隙度或声波孔隙度与岩心分析孔隙度数据，采用回归的方法，建立了安山质沉火山角砾岩储层孔隙度计算模型，其中，中子孔隙度和密度孔隙度组合计算孔隙度平均相对误差为7.5%，中子孔隙度和声波孔隙度组合计算孔隙度平均相对误差为8.0%。

(1)中子孔隙度和密度孔隙度组合

(1)

(2)中子孔隙度和声波孔隙度组合

(2)

式中:φ——孔隙度，%；

ρd——密度测井值，g/cm3；

ρma——骨架密度值，g/cm3；

ρmf——滤液密度值，g/cm3；

ΦN——中子测井值；

ΦNma——骨架中子值；

ΦNmf——滤液中子值；

Δt——声波时差测井值，μs/m；

Δtma——骨架声波时差值，μs/m；

Δtmf——滤液声波时差值，μs/m。

对于未扩径储层，中子孔隙度和密度孔隙度组合计算孔隙度效果好于中子孔隙度和声波孔隙度组合；对于扩径较严重储层，中子孔隙度和声波孔隙度组合计算孔隙度效果好于中子孔隙度和密度孔隙度组合。

2.2 渗透率计算模型

利用6口井的30块安山质沉火山角砾岩岩心分析数据，建立了岩心分析孔隙度和渗透率交会图(图5)，从图中可得孔隙度和渗透率相关性很好，相关系数为0.92，通过孔隙度回归分析的方法，建立了安山质沉火山角砾岩储层渗透率解释模型，即

K=3×10-5φ3.900 7

(3)

式中:K——渗透率，mD。

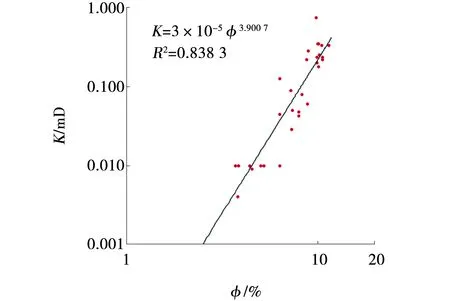
图5 孔隙度和渗透率的关系Fig. 5 Relationship between porosity and permeability

2.3 束缚水饱和度模型

针对致密储层，除了利用孔隙度、渗透率、黏土含量等参数回归建立束缚水饱和度模型之外，研究人员还利用毛管压力实验数据建立J函数与含水饱和度之间的关系，结合J函数概念以及含气高度与储层毛管压力之间的关系，建立了储层含水饱和度的关系式，进而求取储层束缚水饱和度[18-21]。

由于研究区核磁离心实验分析的束缚水饱和度数据很少，因此，针对W断陷沉火山角砾岩气藏受重力分异作用，气高水低，气水界面明显的特点，利用毛管压力数据拟合J函数与含水饱和度之间的关系，结合J函数概念以及含气高度与储层毛管压力之间的关系，建立储层含水饱和度关系式，进而分析不同孔渗下含水饱和度随含气高度的变化关系，确定合适的气水界面高度，从而确定出气柱高度。对于气层，储层的束缚水饱和度等于气柱高度对应的含水饱和度。

利用S1段3块安山质沉火山角砾岩岩样的压汞实验数据，建立“J函数”与含水饱和度交会图(见图6)，拟合得到二者的关系式，相关系数为0.88，其公式为

(4)

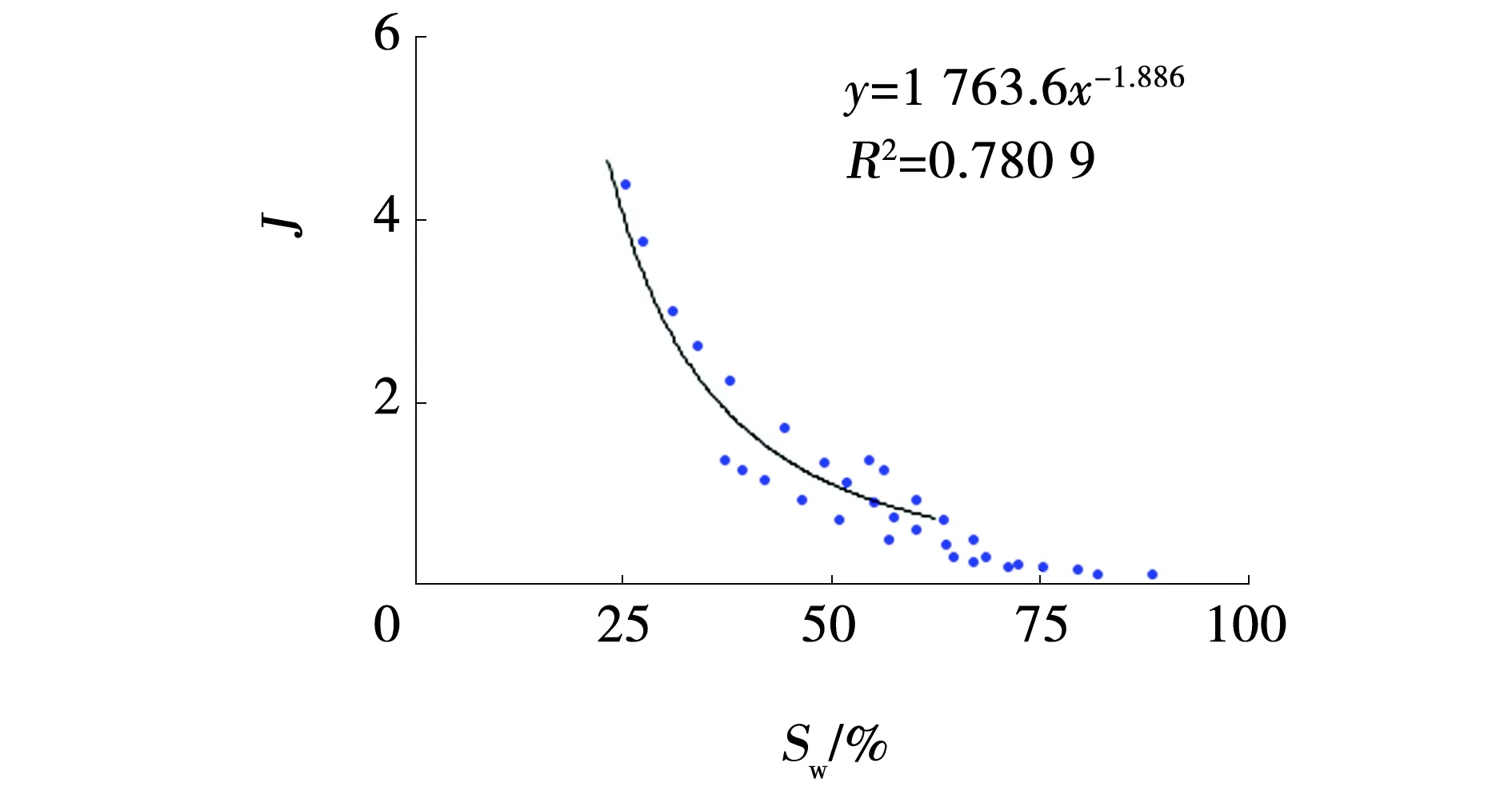
图6 J函数与含水饱和度的关系Fig. 6 Relationship between J-function and water saturation

根据气柱高度H与J函数之间的关系式，建立储层原始含水饱和度关系式，即

Sw(H，K，φ)=e6.498 69-0.530 22 lnH-0.265 11ln(K/φ)，

(5)

式中:Sw——含水饱和度，%；

H——气柱高度，m。

利用气藏剖面研究成果，综合确定自由水面以上63 m为气层。气柱高度(H=63 m)对应的含水饱和度即为储层的束缚水饱和度值。由此建立束缚水饱和度计算公式为

Swi=e6.498 69-0.530 22ln63-0.265 11ln(K/φ)，

(6)

式中,Swi——束缚水饱和度，%。

2.4 储层参数计算精度分析

利用建立的孔隙度、渗透率模型处理A6井安山质沉火山角砾岩储层，并将计算结果与岩心分析数据进行对比。图7给出了储层参数计算值与岩心分析数据的对比结果。图中，GR代表自然伽马，SP代表自然电位，CAL代表井径，RLA1～RLA5代表阵列侧向电阻率，U代表铀，TH代表钍，K代表钾。选用中子密度孔隙度组合计算取心段孔隙度，从图中可以看出，安山质沉火山角砾岩计算孔隙度和渗透率值与岩心分析数据吻合很好，证明建立的储层参数模型计算精度较高。

图7 A6井储层参数计算值与岩心分析值对比Fig. 7 Comparison of calculated results and measured data for well A6

3 储层饱和度解释方法

针对S1段安山质沉火山角砾岩储层孔渗非常低、孔隙结构复杂的特征。选用能描述岩石孔隙结构特征的等效岩石元素理论建立了致密气储层饱和度模型。同时，给出了阿尔奇方程，对比饱和度模型应用效果。

3.1 等效岩石元素电阻率模型

等效岩石元素模型认为饱含水岩石中电荷迁移效率高的小孔隙和电荷迁移效率低的大孔隙为串联导电。其等效体积模型见图8。

根据地层因素公式定义[14-16]可得

F=(1-φ)2/epsφ+1/φ，

(7)

式中：F——地层因素；

eps——孔隙结构效率。

当孔隙空间中存在油气时，含油气纯岩石等效岩石元素模型的体积模型见图9。根据图9可推出含油气纯岩石视地层因素Fa表达式为

(8)

式中，k——流体非均匀分布指数。

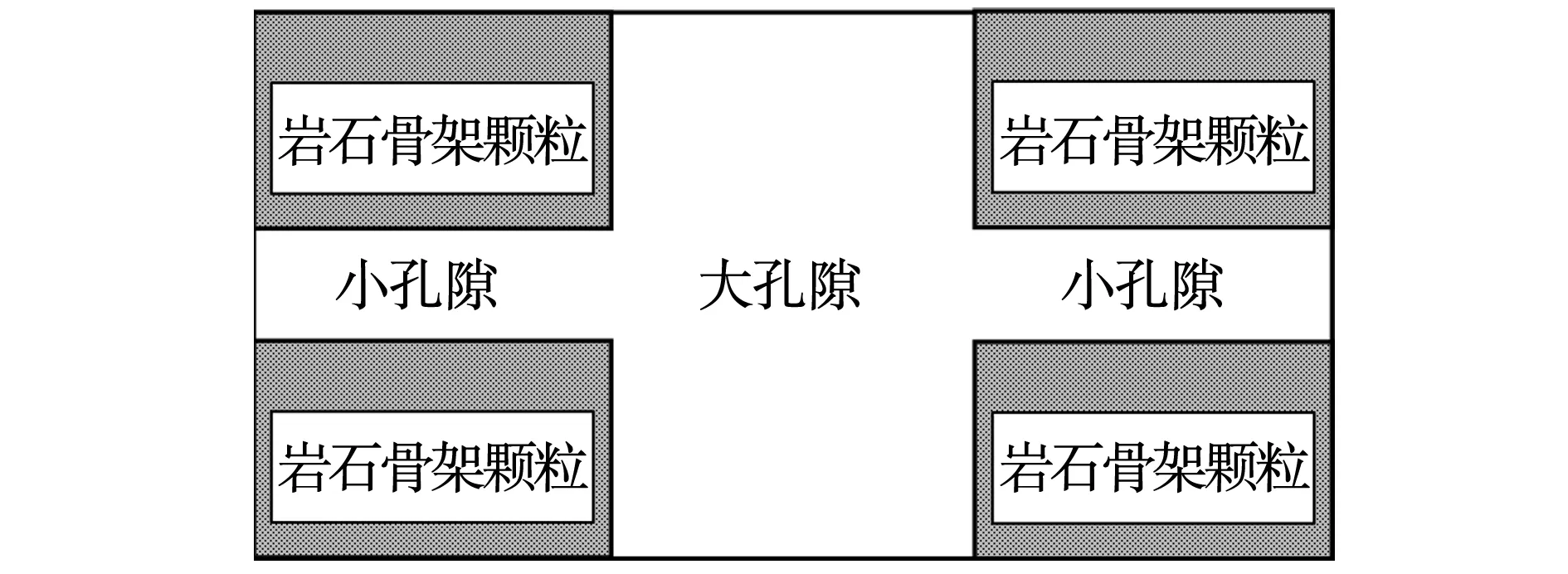
图8 饱含水纯岩石等效岩石元素模型的体积模型Fig. 8 Volume model of equivalent rock element model for water saturated clean rock

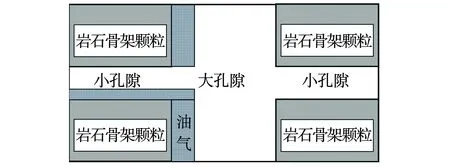
图9 含油气纯岩石等效岩石元素模型的体积模型Fig. 9 Volume model of equivalent rock element model for hydrocarbon bearing clean rock

整理得

(9)

式中：Ct——岩石电导率，S/m；

Cw——地层水电导率，S/m。

利用6块安山质沉火山角砾岩岩心的岩电实验数据，采用最优化技术，确定了等效岩石元素电阻率模型岩电参数，即eps=0.13，K=1.0。

3.2 饱和度模型的优选

通过对6块安山质沉火山角砾岩岩心的岩电规律研究，得出了阿尔奇公式的参数：a=1，m=0.033 5φ+1.518 4(φ为百分数)，b=1.03，n=2.4。

图10给出了A602井安山质沉火山角砾岩储层(104～107)的2个饱和度模型的处理结果对比图。104、105、106层合试，日产气10×103～20×103m3，日产水9 m3，试油结论为气水同层。由图可知，阿尔奇公式计算的含水饱和度(SWA)约为40%，接近束缚水饱和度，无可动水，计算含水饱和度偏低，与试气结果不符；等效岩石元素模型计算的含水饱和度(SWE)在40%～70%之间，有一定的可动水，含水饱和度更为合理。107层上部(2 573～2 583 m)孔渗好、电阻率高，下部(2 583～2 624 m)孔渗降低，电阻率降低，气测峰基比降低，储层上部含气性比下部含气性好；阿尔奇公式计算的含水饱和度接近束缚水饱和度，无可动水，且储层上部与下部含水饱和度差别不大，不符合储层上部与下部的含气性特征变化；等效岩石元素模型计算的含水饱和度高于束缚水饱和度，有可动水，且储层下部含水饱和度比上部含水饱和度增大，符合储层上部与下部的含气性特征变化。等效岩石元素模型引入了孔隙结构效率参数，考虑了孔隙结构变化对储层导电特性的影响，计算的含水饱和度更为合理，优选等效岩石元素模型计算安山质沉火山角砾岩储层含水饱和度。

4 实例分析

利用文中建立的定量解释方法对A102井安山质沉火山角砾岩储层进行处理解释，解释结果见图11。由结果可知，173号层上部(173-1)孔渗低，气测显示比较差，解释为干层；173号层下部(173-2)孔隙度为6.9%，渗透率为0.061 mD，束缚水饱和度为42.8%，含水饱和度为54.6%，解释为气水同层；174号层孔隙度为7.2%，渗透率为0.071 mD，束缚水饱和度为41.1%，含水饱和度为50.1%，解释为气水同层。173、174层合试，放喷瞬间日产气2×103～2.5×103m3，放喷半小时，日产水25 m3，试油结论为气水同层。解释结果与试油结论一致。

5 结 论

(1)针对安山质沉火山角砾岩，优先选用中子密度孔隙度组合计算储层孔隙度，而在井眼扩大时，应选用中子声波孔隙度组合计算储层孔隙度。针对沉火山角砾岩构造气藏，可通过构建J函数的方法计算储层束缚水饱和度。

(2)将等效岩石元素模型引入了孔隙结构效率参数，有效地反映了安山质沉火山角砾岩中孔隙结构变化即导电性影响大的小孔隙与影响小的大孔隙体积之比对岩石导电规律的影响，因此，等效岩石元素导电模型更适合于安山质沉火山角砾岩储层饱和度解释。

(3)利用建立的安山质沉火山角砾岩储层定量解释方法处理实际测井数据，孔隙度、渗透率、饱和度参数计算结果与岩心分析或试油结果吻合较好，证明建立的模型适用于研究区安山质沉火山角砾岩储层定量测井评价。