下肢康复机器人末端的控制方法

沈显庆， 任琳琳

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

随着人口老龄化的发展，我国已经成为脑卒中疾病发生率较高的国家，同时脑卒中疾病很容易引发患者下肢丧失运动功能。因此，越来越多的学者以及科研院所开始关注、研究下肢康复机器人的控制方法，希望为患者设计出通过辅助机器人训练使患者达到正常行走目的的智能设备。下肢康复机器人辅助患者运动，需要避免下肢末端未能达到理想位置，使患者受到二次伤害。因此，对下肢康复机器人末端轨迹进行研究，同样具有重要的意义。王雨等[1]采用了多幂次趋近律的滑模控制器对打磨机器人的末端进行控制，达到抗干扰能力强且趋近平衡点的速率更快。叶梅燕等[2]通过建立高斯几何学的运动特征描述模型，提出了机器人末端运动特征的分析方法，为研究机器人末端控制提供了理论基础。刘延芳等[3]针对机器人末端负载的不确定性，采用迭代最小二乘法对机器人末端负载的质量进行估计，由自抗扰控制器进行补偿，具有一定的稳定性。笔者利用双曲面正切函数的陡度调节滑模控制的切换，设置调节趋近速度的指数项，对下肢康复机器人的末端进行直接控制，以提高机器人的控制效果。

1 结构空间坐标变换

文中以下肢康复机器人末端为研究对象，建立机器人末端空间坐标，设计滑模控制器对其进行直接控制。根据下肢康复机器人末端节点的控制率与机器人关节运动的力矩之间的关系[4]，求解实际为机器人末端提供的力矩，并对下肢康复机器人的末端轨迹进行分析。下肢康复机器人的结构[5]，如图1所示。

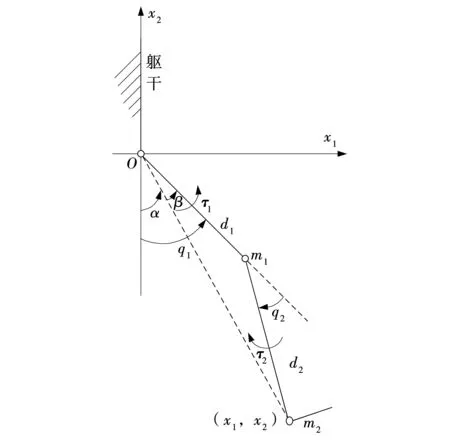
图1 下肢康复机器人结构Fig. 1 Structure of lower limb rehabilitation robot

利用机器人逆运动学原理，对下肢康复机器人进行逆运动学分析，从而求解关节角度q1和q2，由图1可得下肢康复机器人的末端工作空间位置以及角度：

根据余弦定理，可得

则

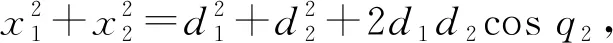
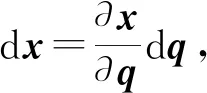
因此，

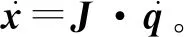
由此可得，表示下肢康复机器人末端点的速度与机器人关节角速度之间关系的雅可比矩阵：

(1)

2 关节动力学模型

一般的机器人关节动力学模型为

(2)

式中：M(q)——n×n阶转动惯量矩阵；

G(q)——n×1阶重力向量；

q——关节变量的向量,q∈Rn；

τ——执行机构施加的关节控制扭矩向量,τ∈Rn；

τd(t)——外界干扰量。

为了实现下肢康复机器人末端位置的精确控制，需要将一般机器人关节动力学模型转换为基于末端位置的动力学方程。根据虚功原理，可得机器人末端的力矩T与关节力矩τ之间的关系[6]：

Τ=J-T(q)τ,

(3)

由式(1)，可得

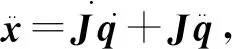
则

(4)

将式(4)代入式(2)，并结合式(3)可得

可得下肢康复机器人末端模型为

(5)

式中：Mx=J-T(q)M(q)J-1(q)；

Gx=J-T(q)G(q)；

3 控制器设计

定义

e(t)=xd(t)-x(t)，

(6)

(7)

式中：xd(t)——理想轨迹；

x(t)——实际轨迹；

Λ——正定矩阵。

设计滑模函数为

(8)

传统的滑模控制律为

(9)

将式(9)代入式(5)可得

(10)

由式(6)～(8)，可得

(11)

结合式(10)，可得

采用双曲面正切函数的滑模控制器

结合式(5)和(11)，可得

4 稳定性证明

取李亚普诺夫函数为

对于双曲面正切函数的控制器有

ks-εsgns+τx)。

根据引理[8-9]可得：

其中，μ=0.278 5。

则

ξμε≤-2λV+b，

式中：λmin(k)——k的最小特征值；

λmax(Mx)——Mx的最大特征值；

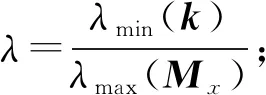
b——常数项,b=ξμε。

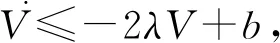
则

由此可知，系统属于渐进收敛，且收敛的速度跟精度取决于ξ、ε、λ。

5 仿真分析

5.1 参数设置

为了更切和实际，以一男子为例对其进行动力学分析计算[11]，该男子体重为 61 kg、身高1 667 mm、d1为462 mm、d2为 393 mm。为了更好地对模型进行动力学分析，根据GB 10000—88《国家成年人人体尺寸》可以计算该男子各段质量，可得m1=8.512 2 kg，m2=2.552 6 kg，则可得下肢康复机器人动力学模型中的参数为[5]：

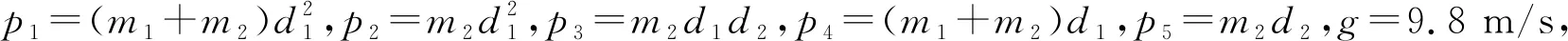
取理想的跟踪轨迹为

初始条件设为

x=[1,0,1,0]，

τx=5sint控制器增益矩阵为

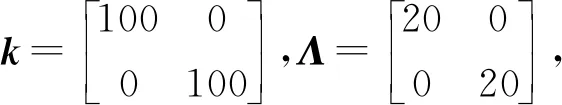
ξ=20，ε=0.1进行仿真。

5.2 结果与分析

图2～6为采用不同的控制器时，下肢康复机器人末端运动的仿真结果。图2～5中的a图为采用传统的滑模控制器得到的仿真图。由图2a、3a可以看出，在下肢康复机器人运动过程中，机器人末端位置和速度跟踪出现较大波动，但是在2 s之前，下肢康复机器人的末端位置与速度跟踪值，都能达到理想的跟踪轨迹。由图4a、5a可知，机器人末端的控制力矩出现了抖振现象以及轨迹收敛的速度比较慢。

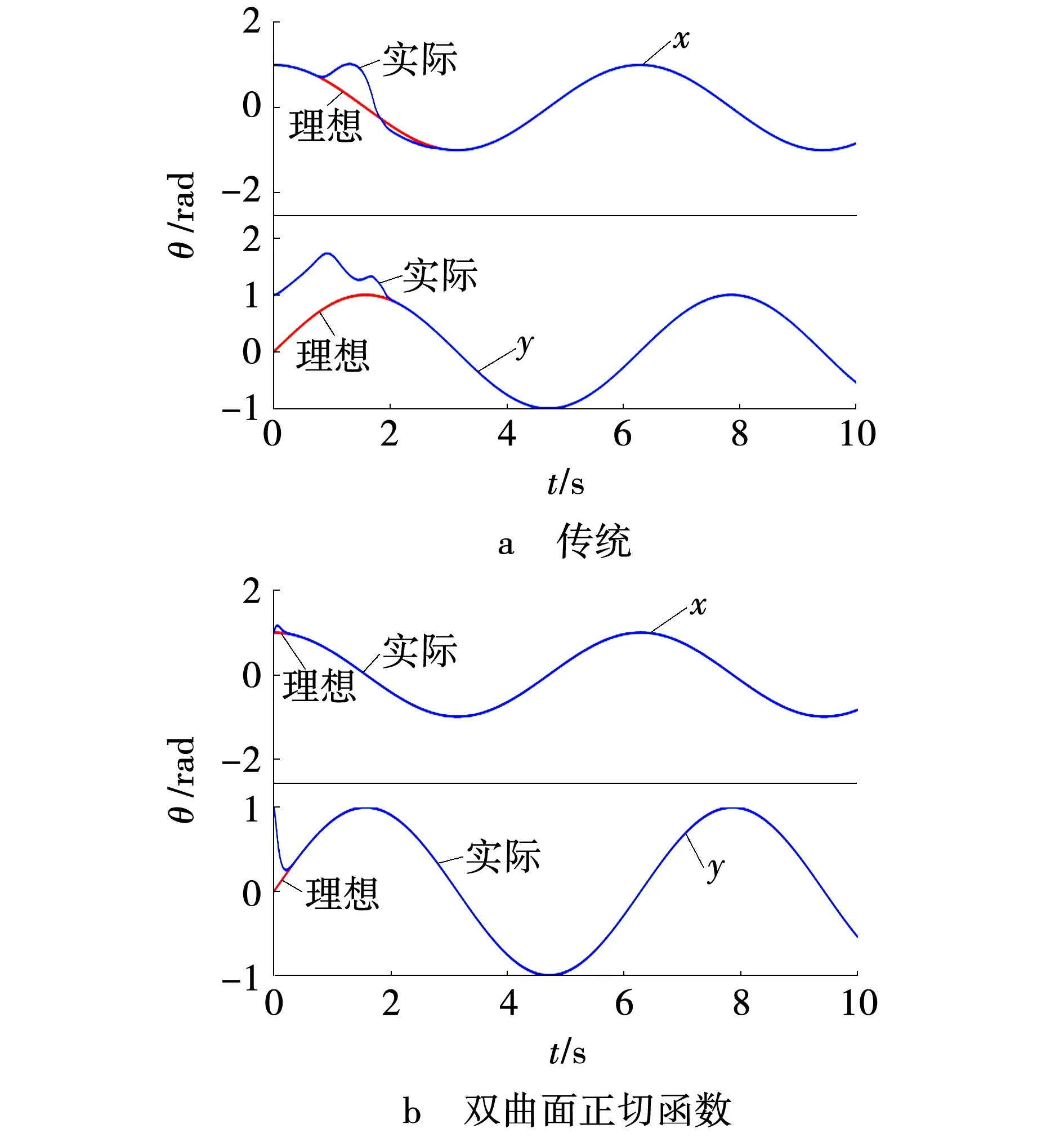
图2 下肢康复机器人末端位置跟踪Fig. 2 End position tracking of lower limb rehabilitation robot

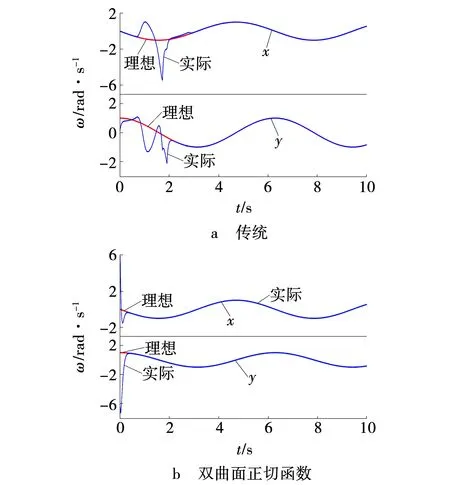
图3 下肢康复机器人末端速度跟踪Fig. 3 Velocity tracking at end of lower limb rehabilitation robot

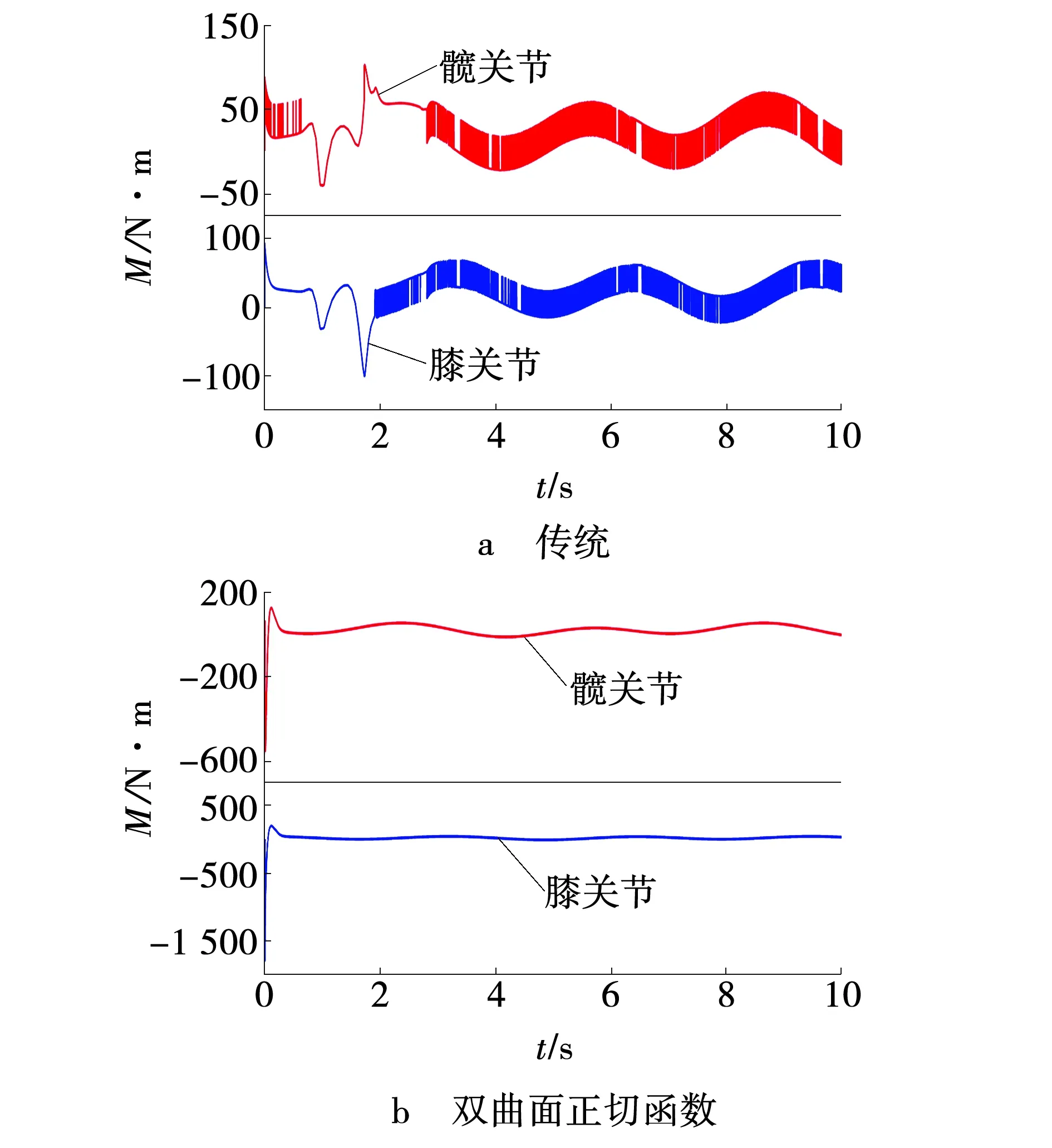
图4 下肢康复机器人末端控制力矩Fig. 4 Terminal control torque of lower limb rehabilitation robot

图5 下肢康复机器人末端轨迹Fig. 5 Distal trajectory of lower limb rehabilitation robot

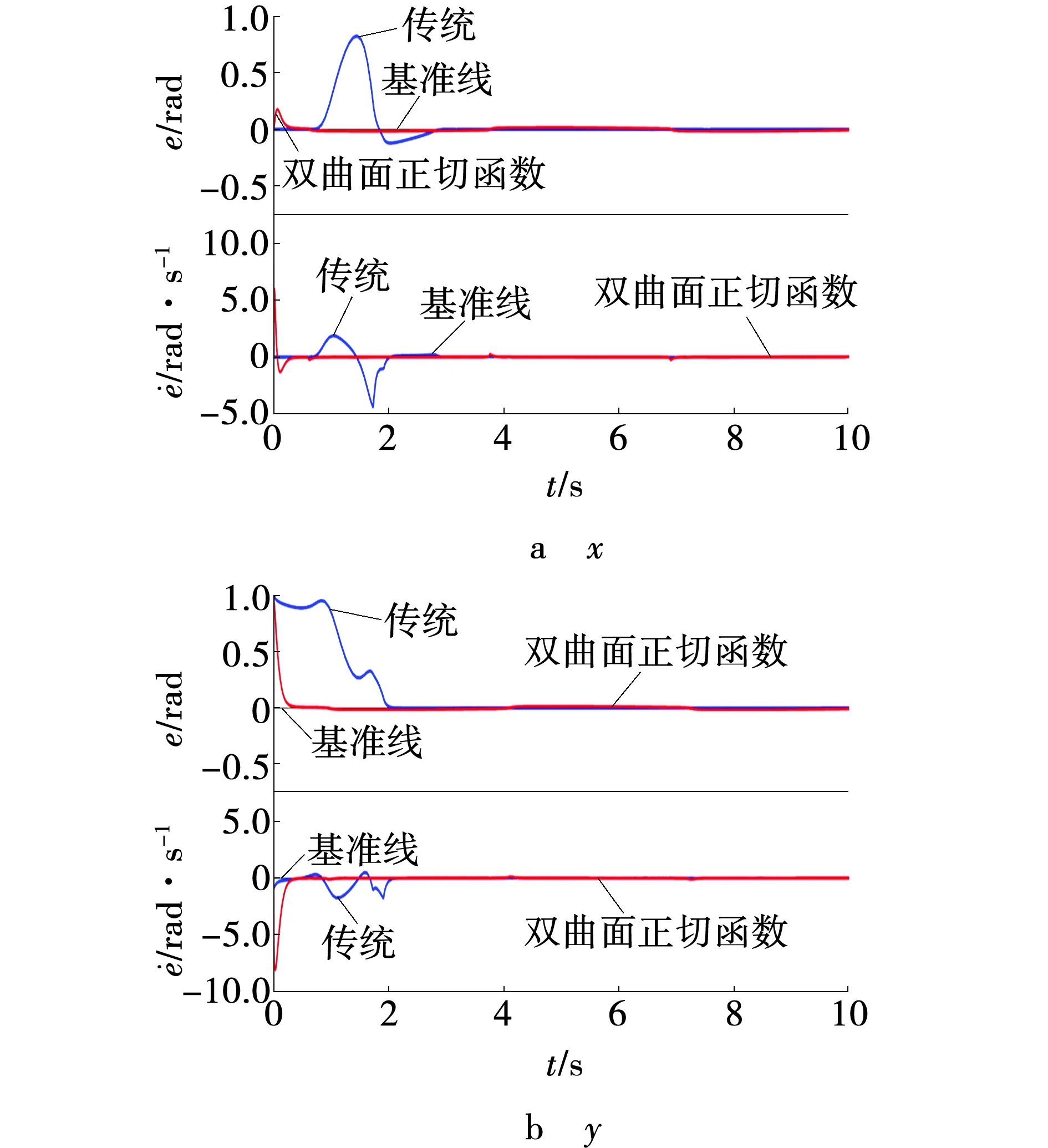
图6 下肢康复机器人末端跟踪轨迹误差分析Fig. 6 Error analysis of end tracking trajectory of lower limb rehabilitation robot

图2～5中的b图为采用双曲面正切函数的滑模控制器得到的仿真结果。由图2b、3b可以看出，下肢康复机器人在运动过程中，机器人末端的位置和速度，能够在极短的时间内达到理想的运动轨迹，由图4b、5b以及图6可以看出，对下肢康复机器人的末端，采用双曲面正切函数的滑模控制，明显的削弱了控制输入的抖振现象，提高了系统的收敛速度，并且缩小了系统存在的误差。

6 结束语

针对传统的控制器对下肢康复机器人末端轨迹跟踪控制存在的收敛速度较慢，以及输入的力矩存在的抖振现象，提出了一种采用双曲正切函数的滑模控制方法，对下肢康复机器人的末端进行直接控制。在Matlab/Simulink的环境下，利用S-Function函数进行仿真实验。采用双曲正切函数的滑模控制器对机器人末端控制的效果更好、收敛速度更快，显著减少了机器人末端输入力矩的抖振。该研究可为下肢康复机器人的跟踪问题提供理论依据。