浅析高中数学概念教学的有效性策略
2020-05-07白哲生
白哲生


摘要:在高中数学教学中,数学概念是重点的教学内容,但是它的抽象性较大,需要学生具有很强的思维能力,故此,导致学生学习起来十分困难。受传统教学方法的影响,很多学生对数学概念理解的不透彻,导致在解决实际问题的时候难以达到学用贯通。因此,为提高对概念的理解,提高数学学习水平,教师要创新概念教学方法,认识高中概念教学的地位和原则,从设计教学情境出发,到对比观察、层层问题解析、数学史学等,使其感知概念、生成概念、理解概念、内化概念,最终提高数学学习效果。
关键词:高中数学;概念教学;有效性
中图分类号:G642;O13-4 文献标识码:A文章编号:1992-7711(2020)24-029
概念是反映对象特有属性的思维形式。数学概念的学习是为了让数学知识的展示更加客观具体,针对各种数学实物、数学思想等进行概括和总结,反映出实际的数学内容,能够减轻数学教学的难度。因此,为促进对高中数学知识的掌握和消化,达到学用贯通的教学目标,教师要认识高中概念教学的地位和原则,通过概念教学方法的创新,提高高中数学课堂教学质量。
一、设计生活情境,感知概念
概念的感知是学习概念的基础。在进行高中数学概念的教学时,设计生活情境,促使其概念的产生有一个清楚的理解,既可以创优教学氛围,又可以促进从感性认识过渡到理性探索,培养科学探究精神。例如,在教学《空间直线与平面垂直》数学内容时,为让学生理解直线与平面垂直的概念,能够运用判定定理证明一些空间位置关系命题。在概念教学时,可以利用互联网手段,在微课课件中播放:将书本打开直立于桌面、在开门过程中,门轴与地面始终垂直、日光下直立于地面的旗杆以及地面上的影子等场景,由生活实例入手,引导学生感知垂直。然后为学生准备三角形纸片,将三角形纸片三个点分别定为A、B、C,过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起来放置到桌面上,让学生思考折痕AD与桌面的位置关系是什么?如何翻折才能使得折痕AD與桌面垂直?为什么?通过生活实例的引入以及动手探索实验验证,这样既可以促进思维发展,又可以丰富认知结构,完成感性到理性的升华,让学生认识空间直线与平面垂直的概念,体会概念发生以及发展的过程,促使概念教学更具趣味性、探索性。
二、新旧对比分析,生成概念
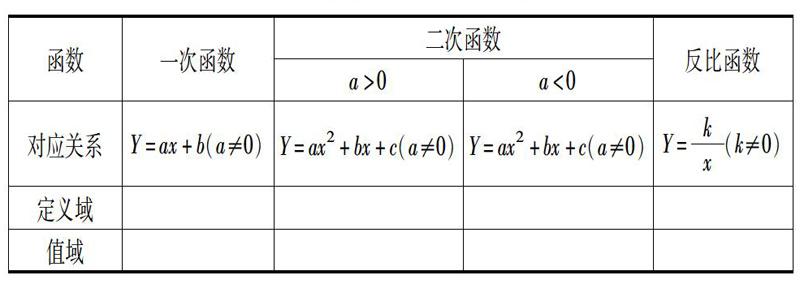
高中数学是初中数学的升华,是知识进一步的完善,其中有着潜在的关联。那么,在进行高中数学概念教学的时候,使其认识概念的生成和发展过程,可以通过新知识与旧知识的结合,进而在学习和复习的过程中,实现概念外延,让学生更好地理解旧概念,从而生成新的概念。例如,在教学《函数概念及其表示》的内容时,旨在让学生进一步体会函数是描述变量之间的对应关系,能够运用集合与对应的语言刻画函数,体会对应关系刻画函数的作用,理解函数概念符号y=f(x)。那么,在讲解函数概念的时候,可以让学生就以下内容进行分析思考,如:
围绕表格让学生思考分析它们所对应的定义域、值域、对应法则等,然后回归课本内容,分别引导学生思考以下问题:
问题1:某复兴号高速列车加速到350km/h后保持匀速运行半小时,这段时间内,列车行进的路程为S与时间t的关系为?
问题2:某电气维修公司要求工人每周工作至少1天,至多不超过6天,如果公司确定的工资标准是每人每天350元,而且每周付一次工资,你认为怎样确定一个人每周的工资,一个工人的工资为W是他工作天数D的函数吗?
问题3:
围绕北京市空气质量指数变化图,如何根据该图确定这一天内任一时刻t的空气质量指数的值I,I是t的函数吗?
通过问题1到问题3的综合分析,引导学生思考上述函数问题的共同特征是什么?在回归初中函数概念的基础上,通过层层引导引出高中函数相关内容,实现概念生成,让学生更加真实的理解y=f(x)的概念,利用对比分析,引导其认识函数三要素,提高对函数概念的掌握和消化。
感悟:在初中的时候,学生对函数概念已经有了一个初步的了解,为此,在高中讲解函数概念的时候,为让学生深入理解,可以通过回顾旧知为辅助,在知识回顾的基础上,实现自然过渡,培养函数学习自信心,然后通过问题链进行对比分析,使其通过比较、探索,从了解上升到理解掌握,在经历回忆、探索的过程中,唤醒学生的感悟能力,使之对函数概念有一个全面的地认识,让学生能够对函数概念进行归纳。
三、利用问题探究,理解概念
问题探究是数学教学的重要组成部分,也是提高问题解决能力的重要教学目标。在高中数学概念教学中,之所以深化概念教学,是基于在理解概念的基础上,使其能够学用贯通,培养灵活解决问题的能力。那么,在教学的时候,教师可以反方向进行教学引导,依据问题为核心,在问题解决分析的过程中,回归概念,使其理解消化,完成教学目标。例如,在教学《指数函数》的内容时,主要是让学生理解指数函数的概念、性质,能够运用指数函数知识解决简单的数学问题,培养函数思想,可以从问题入手,如:
问题:在2000年年底我们人口已经达到了13亿,那么,经过了20年,倘若人口增长率控制在1%,那么现在,我国的人口数最多为多少?
在解决这一问题的时候,让学生根据每一年的增长情况为基数,引导其发现数学规律,最后成功解决问题,如:
2000年 人口约13亿
经过1年 人口约13(1+1%)亿
经过2年 人口约13(1+1%)(1+1%)=13(1+1%)2亿
经过20年(2020) 人口约13(1+1%)20亿
通过规律探索,引导其设今后人口平均增长为1%,经过x年后,我国人口数为y,根据函数y=13(1+1%)x成功解决问题,在解决问题,探索问题、分析问题的基础上,导出指数函数概念,促进学生的数学思维,让学生正确运用数学概念进行学习,解决实际问题,加强知识的运用。
感悟:一个概念的形成和发展,是呈螺旋上升,是逐步深化的,为此,在教学的时候,教师要遵从概念教学的最终目的,以有效解决问题为核心,引导学生进行学习探索。通过问题探索,让学生的思维发展更加灵活,促进学生的数学思维,让学生正确运用数学概念进行学习,解决实际问题,加强知识的运用。
四、结合数学史学,内化概念
数学概念是经过长久历史探索、分析,演变而成的,而数学史作为学生认识数学概念本质的有效资源。在高中数学课标中明确提到:要提高学生对数学知识的掌握,不仅要使其会解决数学课本问题,还要引导其认识数学史,认识概念本质,在探寻本源的基础上,促进思维发展。那么,在数学概念教学中,为内化概念,达到数学课标要求,可以结合数学史学内容,利用数学史促进学习、思考。
例如,在教学《平面向量的概念》的内容时,旨在让学生了解向量的实际背景,理解平面向量的概念和向量的几何表示,掌握向量的模、零向量、单位向量、平行向量、相等向量、共线向量等概念。教师可以在课前为学生讲述数学史学知识向量的由来,从数学发展史入手,让学生理解向量的概念,结合生活实际出发,让学生思考一下在小河中划船,逆流而上和顺流而下的感觉有何不同?随后进入数学史,如:
向量又称为矢量,最初被应用于物理学,如物理学中的力、速度、位移、电场强度、磁感应强度等都是向量。在公元前350年前,古希腊著名学家亚里士多德就知道了力可以表示成向量……最先使用有向线段表示向量的是英国大科学家牛顿。从数学发展史入手,让学生在理解概念的时候,将空间性质与向量运算联系,培养数形思想,使其运用数形思想理解向量概念。如在理解平行向量、共线向量与相等向量时,可以为其引导其绘制以下图形,如:
在梯形ABEF中,向量AB,向量CD,向量EF是一组平行向量,因为可以在空间向量相等平移,所以可以将两个平行向量移动到AB所在的同一条直线上,如:
感悟:数学史是概念产生、生成、发展、演变的历史,因此,在教学的时候,借助数学史的教学,让学生对数学概念的学习更加通透,彻底提高学生的学习能力,形成正确的数学思维。所以在进行数学教学时,要巧妙借助数学史来开展教学。要善于利用数学史,在探寻本源的基础上,渗透数学思想方法,感悟概念生成的核心。
综上所述,平行向量也叫共线向量。通过数形探索分析,渗透数学思想方法,以及数学史学知识的认识理解,提高对数学概念的认识。高中数学概念教学能提高数学学习能力。因此,教师要重视概念教学,围绕生活实际、通过新旧对比、问题探究、史学融合等,促使其感知概念、生成概念、理解概念、内化概念,从本质上深入理解,提高学习的广度和深度。
参考文献:
[1]石义霞.高等数学概念教学策略[J].西部素质教育,2020,6(14):156-157.
[2]王兴.基于深度学习下的高中数学概念教学[J].试题与研究,2020(21):83.
[3]祝玉芳.浅析核心素养导向下的高中数学概念教学[J].中学教学参考,2020(21):35-36.
(作者单位:甘肃省嘉峪關市酒钢三中,甘肃 嘉峪关 735100)
