利用扩展的简单方程法求解时空分数阶偏微分方程

赵云梅，杨云杰

（1.红河学院数学学院，云南蒙自 661199; 2.昆明学院数学系,昆明 650214）

1 引言

由于分数阶导数是非局部算子，对它进行刻画时依赖于初始时刻的历史状态，因此分数阶模型比整数阶模型在描述某些现象和反映物体的某些性质时更精确，物理意义更清晰，表述更简洁，它已经成为复杂力学与物理工程数学建模的重要工具之一，已被广泛地应用到粘弹性阻尼器、流体力学[1]、生物医学工程、图像处理[2]、信号处理和系统识别、振动与控制[3]、地震分析[4]等领域。目前分数阶微分方程已成为数学、物理、医学和经济等领域的研究热点。

分数阶非线性偏微分方程并不是整数阶非线性偏微分方程的平行推广，许多整数阶微积分的性质在分数阶微积分中不一定成立，若是要获得分数阶微分方程的精确解就变得很困难。尽管求解分数阶偏微分方程的精确解较为困难，但是分数阶微积分是由整数阶微积分引出的，在求其精确解时，可以针对不同方程的特征，探索并构造相应的求解方法是可以实现的。目前国内外学者提出和发展了一些求解方法，如：分数阶子方程法[5-6]、分数阶Riccati展开法[7]、分数阶(G'/G)-展开法[8-10]、变量分离法[11]、简单方程法[12]、分数阶Jacobi椭圆方程法[13]和分数阶首次积分法[14]等。

简单方程法和扩展的简单方程法[15]是求解整数阶微分方程非常有效的一种方法，广大学者运用该方法获得了许多整数阶微分方程的精确解。本研究利用分数阶复变换和扩展的简单方程相结合，提出一种求解分数阶微分方程精确解的新方法，该方法直观、简单有效。

2 预备知识

整合分数阶导数：

设的阶导数的定义为：

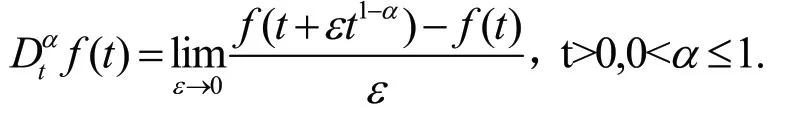
具有如下性质：

设在时可微，则有

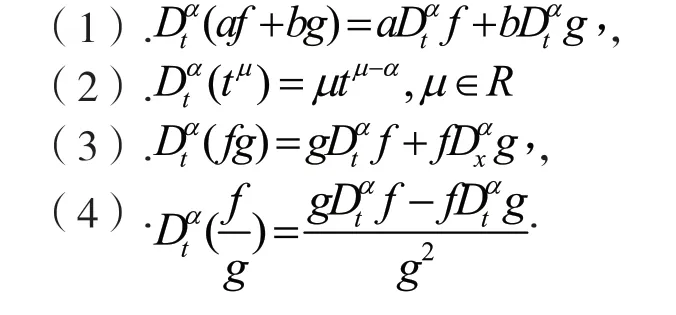
3 方法简述

考虑如下分数阶微分方程：

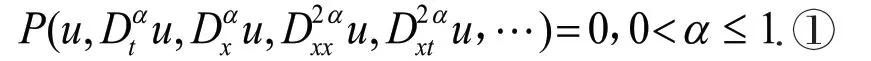
其中是待求函数关于自变量和的分数阶导数，是关于函数及其偏导数的多项式。

为求解方程①的精确解，引入一个复变换：

其中为待定常数，把②代入①式得：

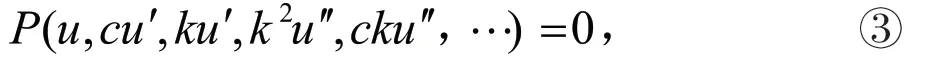
假设式③的解可以表示为如下形式：

其中为待定常数，且，正整数通过平衡③式中的最高阶导数项和非线性项来确定，满足：

其中为常数，由文献[15]知方程⑤的解为：

把④代入③式，利用⑤和⑦，③的左边就可以化为关于的多项式，令它们的各次幂系数为零，便得到一组关于待定常数的代数方程组，求解该方程组得到相关常数，最后代入④式，便求出方程①的精确解。

4 应用

下面考虑一个脉冲时空分数阶非线性微分方程[16]

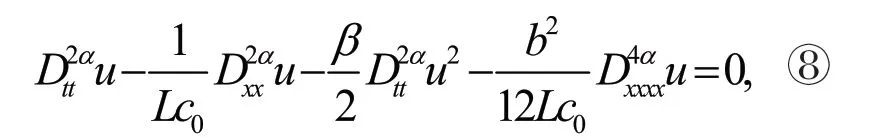
2018年,文献[17]用扩展的函数法和广义的Kudryashov方法探讨该方程，得到了一些精确解，下面将用上述方法求解该方程。

把复变换②代入⑧可得：

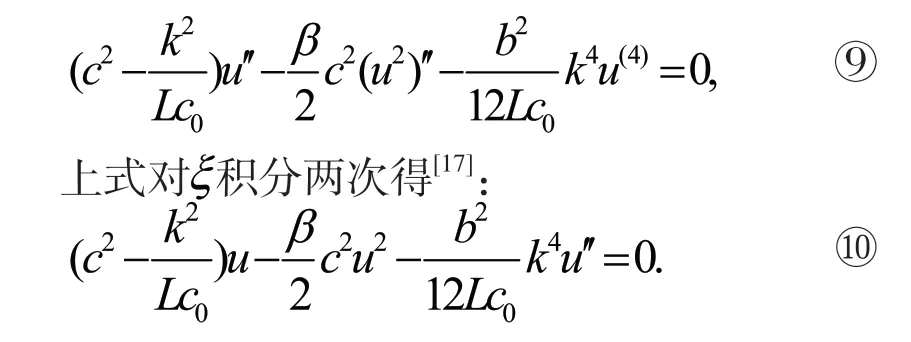
平衡⑩中最高阶导数项和非线性项得，可得即

其中为待定常数，把⑪代入⑩式结合⑤和⑦，⑩的左边就可以化为一个关于和的多项式，令它们的各次幂系数为零，便得到一组关于和的代数方程组，利用Maple求解该方程组得如下解：

（1）

把⑫、⑬ 代入⑪，可得方程⑧的精确解：

5 部分精确解的波形图

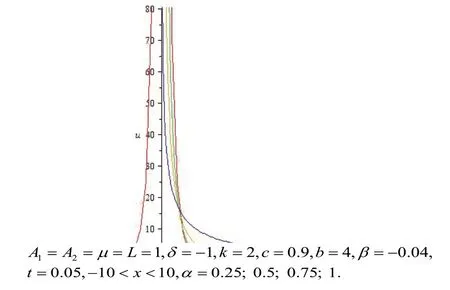
图1 的二维波形图

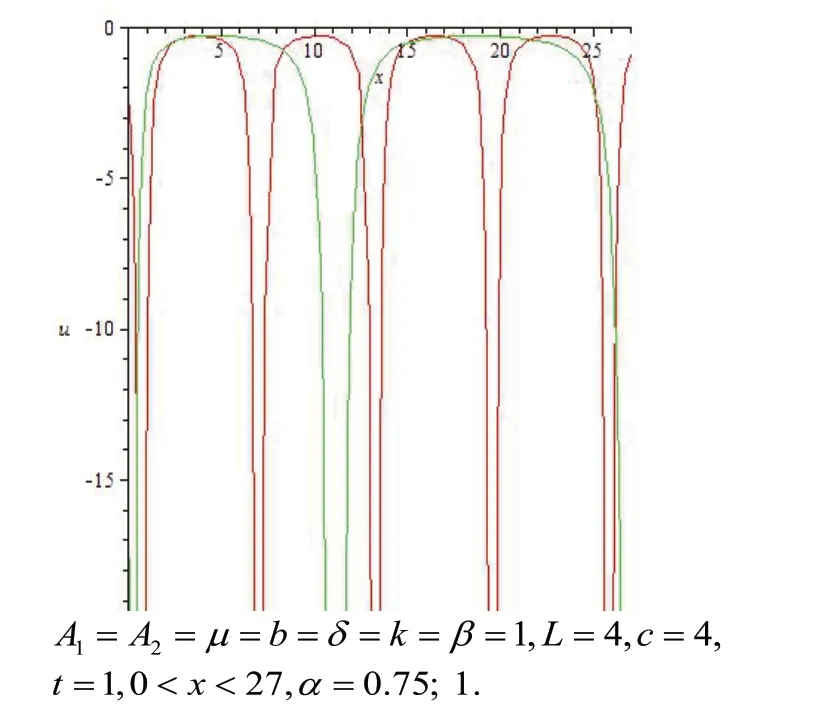
图2 的二维波形图

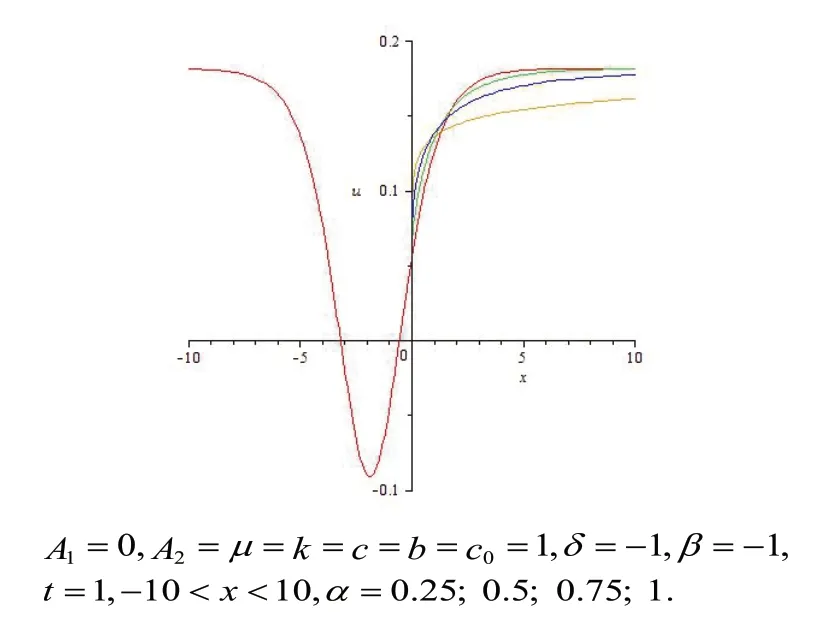
图3 的二维波形图

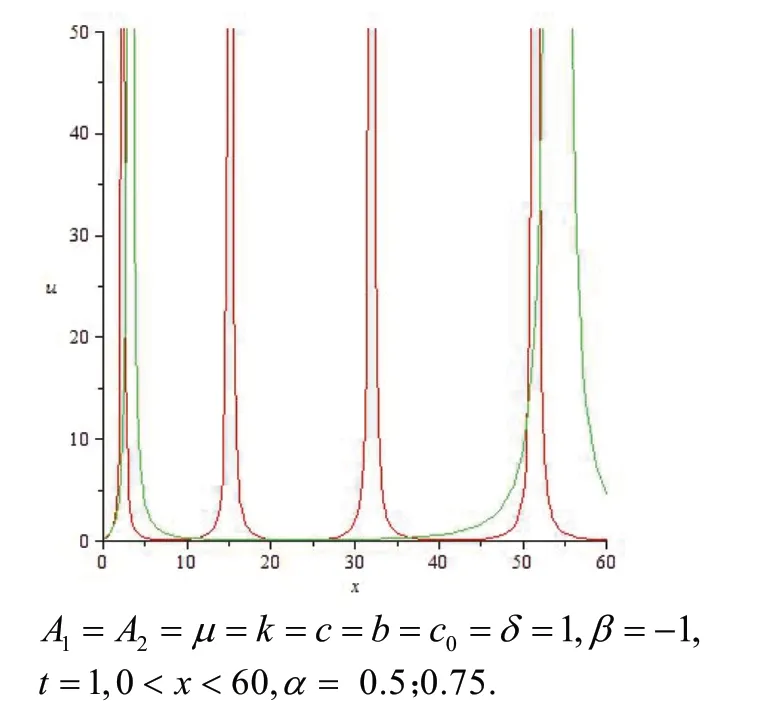
图4 的二维波形图

6 结论

本文把分数阶复变换和扩展的简单方程法相结合，提出了一种求解时空分数阶非线性微分方程精确解的新方法，为了展示该方法的实效性，运用该方法求解了一个脉冲时空分数阶非线性微分方程，获得了该方程的许多用双曲函数、三角函数和有理函数等表示的精确行波解，并运用数学软件Maple绘出部分精确解在不同参数、取不同值的二维波形图，这对我们进一步理解复杂的非线性物理现象和分数阶微分方程的原理具有一定的帮助。本文中提出的方法在求解时空分数阶微分方程精确解时具有简洁、直观、有效的特点，也可以推广到求时间分数阶、空间分数阶微分方程的精确解。