摇摆条件下喷淋液滴运动特性研究
2020-05-07吴廉巍闫超星杜为安刘成洋
吴廉巍,闫超星,杜为安,*,张 翼,刘成洋
(1.海军装备部驻武汉地区第二军事代表室,武汉 430064;2.中国舰船研究设计中心,武汉 430064)
海上浮动平台在发生破口失水事故或者主蒸汽管道破裂事故时,高温、高压蒸汽进入受限空间,导致内部温度、压力迅速升高。为有效抑制压力增长幅值并维持好的气密性,通常设置喷淋系统,其功能是向受限空间内喷出冷却水,使部分蒸汽冷凝,保证其内部压力始终低于设计压力[1-3]。鉴于喷淋液滴动力学特性决定了喷淋系统的冷凝效果,密切影响着系统设计方案,学者们针对竖直条件下液滴的动力学特性开展了广泛研究[4-6]。Porcheron 等[7]采用TOSQAN试验装置开展了喷淋液滴在混合气体空间的动力学特性研究,获得了液滴速度分布、液滴尺寸、气体体积浓度、混合气压力和温度变化趋势,探究液滴与混合气体间的传热传质机理;祝杰等[8,9]对喷淋塔内的液滴动力学特性开展了试验研究。研究表明:空塔内液滴直径是影响终端沉降速度的重要参数,液滴的临界尺寸随空塔气速的增加而增大,环境气速和液滴尺寸是影响液滴在空气中停留时间的主要因素;邓丰等[10]建立了单球体液滴在饱和蒸汽中的动力学模型,对不同尺寸、初始速度和喷射角度的液滴的动力学参数进行数值计算。计算结果表明,在液滴离开喷头后,短时间内水平速度降低为零,竖直方向最终趋近于相同的平衡速度。
近年来,学者们的研究表明海洋条件对流体的流动特性影响显著[11-13]。研究结果表明,摇摆条件对密度差较大的两相工质流动特性的影响主要体现在重力的周期性变化上,海洋环境引起的附加惯性力影响与重力相比可近似忽略[14,15]。然而针对摇摆条件下喷淋液滴的动力学特性研究尚无公开发表的学术成果,本文以海上浮动平台喷淋液滴在空气环境下的运动特性为工程背景,建立了液滴在空气环境中的动量方程,分析液滴初始直径、初始速度、喷射角度及摇摆参数对液滴空间分布及运动轨迹的影响。
1 摇摆条件下液滴模型的建立
针对摇摆条件下单个球形液滴建立动量方程,假设喷淋液滴初始为球体,且运动过程中形状维持不变,文献[16]分析了喷淋液滴在竖直条件下空气环境中的动力学特性,指出液滴在空气环境运动中受到重力、浮升力、附加质量力、玛格努斯力、萨夫曼力以及曳力的综合作用,考虑到汽液相间密度差和空气环境中不存在速度梯度,其中的附加质量力、玛格努斯力、萨夫曼力可忽略不计;而在海洋条件下,流体运动过程中除了受到上述力之外,还会受到附加惯性力的影响[17]。摇摆条件下汽液两相流道内气泡的受力分析表明,摇摆引入的附加惯性力与重力浮力相比可以忽略[15],由于液滴和气泡均可作为流体质点分析,摇摆条件下液滴在空气环境中的受力与泡状流中气泡的受力可进行类比分析。因此,摇摆运动对进入空气环境中液滴的运动轨迹的影响可基本忽略,摇摆运动主要影响液滴离开喷头瞬间的初始状态,进而影响其运动轨迹。液滴离开喷头后,液滴动力学特性主要受重力Fg、浮升力Fb和曳力Fd的综合作用,液滴与时间相关的动量方程[10]如下:

式中,Md——液滴相关的质量,kg;
Fg、Fb——与液滴体积相关的力,分别由ρdVdg和ρaVdg计算,N;
Pd、ρa——水和空气的密度,kg∕m3;
Vd——液滴的体积,m3。
Fd的计算关系式为:
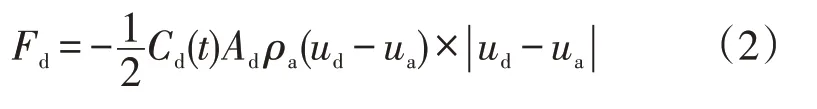
式中,ud——液滴速度,m∕s;
Ua——空气速度,m∕s;
Ad——液滴在运动方向上的表面积,m2;
Cd(t)——液滴与时间t相关的阻尼系数。
式(1)的求解过程可见文献[16]。
摇摆条件下液滴运动轨迹的分析模型如图1 所示。选取大空间喷头的垂向方向为分析面,设定摇摆中心轴为喷头所在位置,空间场沿摇摆中心轴做简谐摇摆运动,图中,θ为t时刻摇摆角度,定义逆时针旋转为正;Φ为液滴离开喷头的初始喷射角度,分析地球坐标系xoy下滴液的动力学特性,原点o为喷头所在位置,需要指出的是本文中液滴的运动轨迹均为相对喷头,即摇摆中心。

图1 摇摆条件下液滴运动轨迹分析示意图Fig.1 Schematic diagram for analysis of droplet trajectory under rolling condition
摇摆运动规律如式(3)所示:
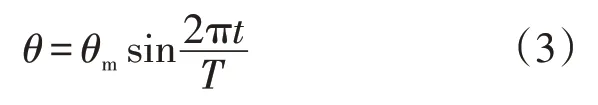
式中,θm——摇摆振幅,(°);
T——摇摆周期,s。
由式(3)可得摇摆角度随时间的变化趋势,如图2 所示,其中摇摆工况为θm=15°、T=8s,表示在一个摇摆周期内,固定时间间隔的液滴的出发时间和角度的对应关系。
2 计算结果分析
2.1 摇摆对液滴运动影响的机理
由本文第一章分析可知,摇摆运动主要影响液滴离开喷头瞬间的初始状态进而影响其运动轨迹,而液滴的初始速度和初始直径是受喷头前管路系统水力特性的影响,实际工程中喷淋系统往往采用喷淋泵驱动喷淋流体,鉴于学者研究中表明,摇摆工况对强迫循环回路中流量和压力无明显影响[18],因此,摇摆工况主要通过影响液滴喷射角度来影响液滴的动力学特性。以摇摆工况θm=15°、T=8 s 为例,8 s 时液滴的空间分布和历史运动轨迹如图3所示。
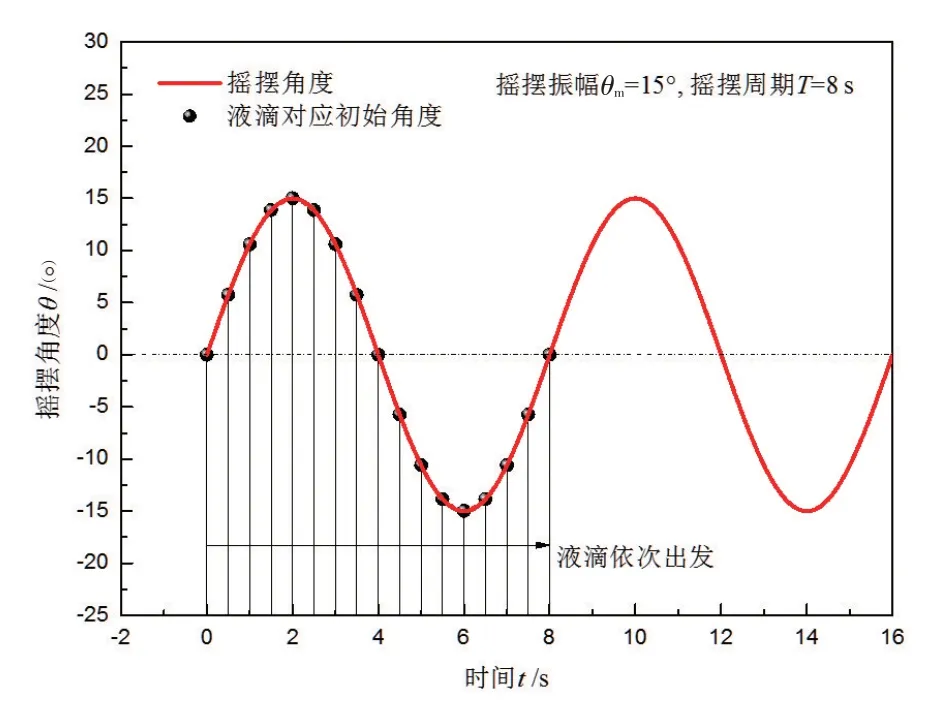
图2 液滴出发时间和角度的对应关系图Fig.2 The corresponding diagram of droplet departure time and angle
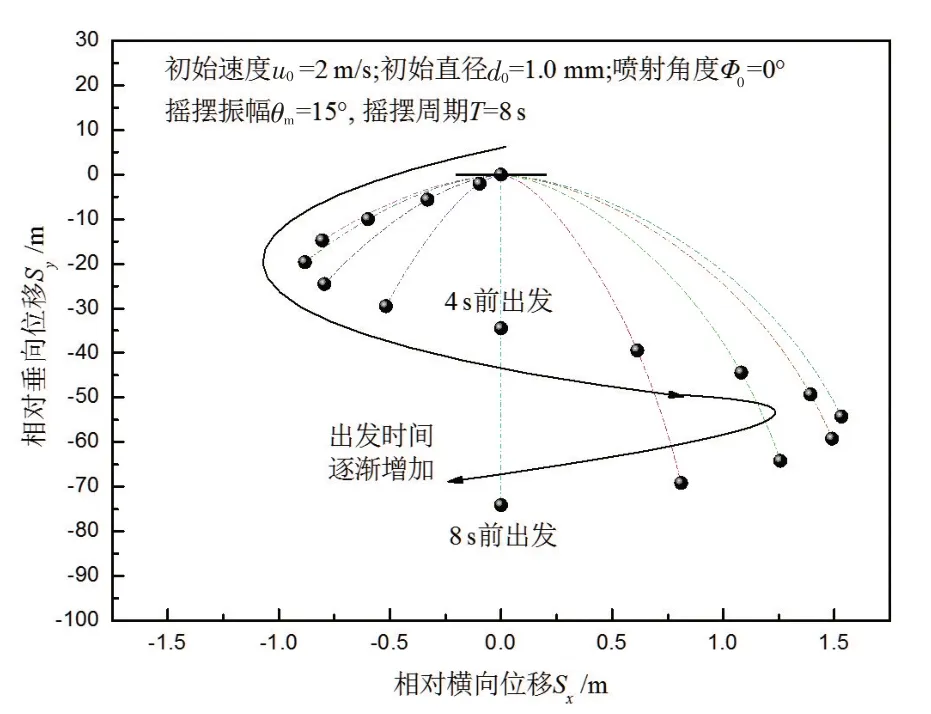
图3 摇摆条件下第8 s液滴空间分布Fig.3 Spatial distribution of droplets under rolling condition at 8 s
由图3可知,出发时喷射角度相同的液滴沿着相同的轨迹运动,由于正向摇摆角度的出发时刻早于负向摇摆角度,导致喷射角度相同的正向液滴的运动时间更长,达到的相对横向和垂向位移也越大,因此,液滴分布表现出相对横向位移的波动峰值随时间推移逐渐增大,直到液滴的横向速度消失时达到最大。
2.2 喷嘴设计参数的影响
实际喷淋系统设计中,喷淋系统流量、压力、喷淋头布置、喷淋头型式是影响喷淋液滴初始直径、初始速度和喷射角度的关键因素。喷淋头型式包括喷口直径、喷嘴型式等。下文通过针对不同关键因素对雾化机理影响现象的分析来阐述喷淋液滴的动力学特性。
2.2.1 初始直径对空间分布的影响
喷淋液滴的初始速度为2 m∕s、喷射角度为0°时,选取摇摆工况θm=10°、T=8 s,液滴初始直径对运动轨迹的影响如图4 所示。需要指出的是,本节选取的摇摆工况为典型海上浮动平台的运行工况,便于在同一摇摆条件下分析液滴初始参数对空间分布的影响。图4为自第一个液滴离开喷头后第8 s 的瞬时时刻。计算结果表明,不同液滴在初始直径条件下,摇摆时液滴离开喷头后沿相对横向位移正负向两侧依次分布,出发喷射角度相同的液滴,在相对横向位移达到最大前,先离开喷头的液滴达到的相对横向位移大于后离开的液滴。液滴直径越大,相同时间内达到的相对垂向位移越大,摇摆运动时液滴的相对横向位移的波动幅值越大,相应的液滴覆盖范围也越大。结果表明,相同条件下一定范围内的摇摆运动有利于提升直径较大液滴的覆盖范围。

图4 液滴初始直径对空间分布的影响Fig.4 Effect of droplet initial diameter on spatial distribution
2.2.2 初始速度对空间分布的影响
喷淋液滴初始直径为1 mm、喷射角度为0°时,选取摇摆工况θm=10°、T=8 s,液滴初始速度对运动轨迹的影响如图5所示,图中为自第一个液滴离开喷头后第8 s 的瞬时时刻。计算结果表明,液滴的初始速度为1 m∕s和2 m∕s时,出发喷射角度相同的液滴在相对横向位移达到最大前,先离开喷头的液滴达到的相对横向位移大于后离开的液滴,初始速度越大,达到最大横向位移的时间越短;液滴初始速度为4 m∕s 时,位于5~7 s 时间段内的液滴已经达到正向横向位移的最大值。液滴初始速度越大,摇摆运动时液滴的相对横向位移的波动幅值越大,相应的液滴覆盖范围也越大。结果表明,相同条件下一定范围内的摇摆运动有利于提升初始速度较大液滴的覆盖范围。
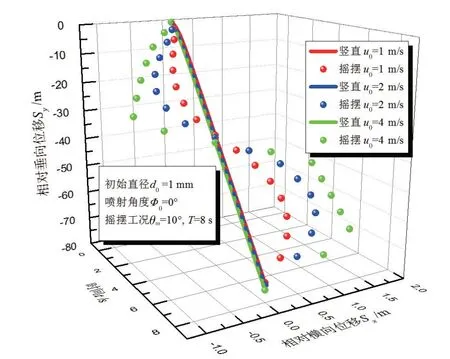
图5 液滴初始速度对空间分布的影响Fig.5 Effect of droplet initial velocity on spatial distribution
2.2.3 喷射角度对空间分布的影响
喷淋液滴的初始直径为1 mm、速度为2 m∕s时,选取摇摆工况θm=10°、T=8 s,液滴喷射角度对运动轨迹的影响如图6所示,图中为自第一个液滴离开喷头后第8 s 的瞬时时刻。计算结果表明,不同的液滴喷射角度条件下,摇摆时液滴离开喷头后沿相对横向位移正负向两侧依次分布,出发喷射角度相同的液滴,在相对横向位移达到最大前,先离开喷头的液滴达到的相对横向位移大于后离开的液滴。液滴喷射角度越大,同一时刻液滴的相对横向位移越大,摇摆运动时液滴的相对横向位移的波动幅值越小,相应的液滴覆盖范围也越小。结果表明,相同条件下一定范围内适当增大喷射角度有利于抑制摇摆运动对液滴运动轨迹的影响。
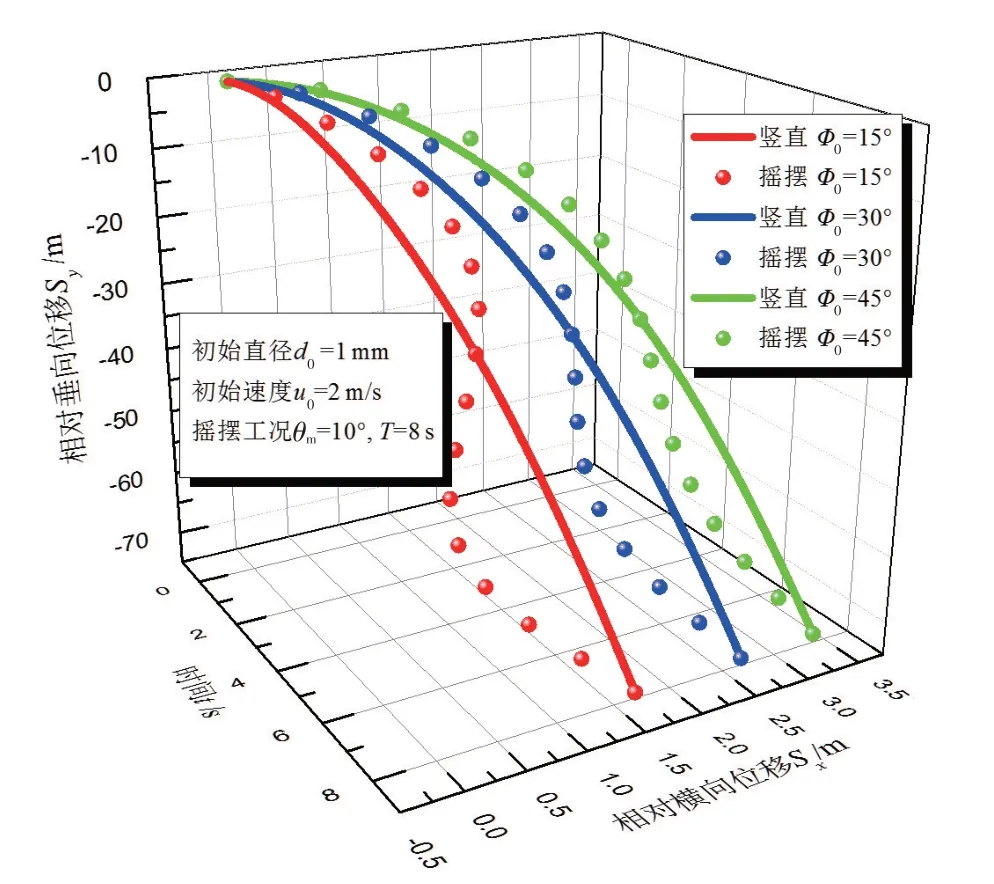
图6 液滴喷射角度对空间分布的影响Fig.6 Effect of droplet injection angle on spatial distribution
2.3 摇摆参数对空间分布的影响
喷淋液滴的初始直径为1 mm、速度为2 m∕s、喷射角度为0°时,摇摆参数对运动轨迹的影响示如图7 所示。其中,摇摆周期T=8 s,自第一个液滴离开喷头后第8 s 的瞬时时刻,摇摆振幅对运动轨迹的影响如图7(a)所示;摇摆振幅θm=15°,自第一个液滴离开喷头后第12 s的瞬时时刻,摇摆周期对运动轨迹的影响如图7(b)所示。计算结果表明,摇摆振幅越大,同一时刻液滴的相对横向位移越大,相对横向位移的波动幅值越大,相对横向位移的波动时间间距与摇摆周期相同,波动幅值对应的时刻与摇摆振幅一致,如图7(a)所示;摇摆周期还会影响相对横向位移的波动时间间距,摇摆周期越大,波动间距越长,但摇摆周期对相对横向位移的波动幅值无明显影响。不同摇摆周期条件下,相对横向位移的波动幅值与倾斜15°工况运动同一时刻的液滴空间位置相同,如图7(b)所示。
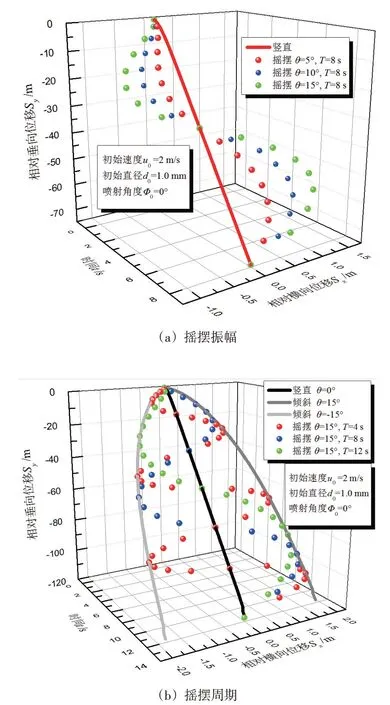
图7 摇摆参数对运动轨迹的影响Fig.7 Effect of rolling parameters on spatial distribution
3 结论
本文以海上浮动平台喷淋系统在空气环境下的运动特性为工程背景,建立了海洋条件下液滴在常温、常压空气环境中的动力学特性分析模型,分析液滴的初始直径、初始速度、喷射角度及摇摆参数对液滴空间分布及运动轨迹的影响,主要结论如下。
(1)摇摆时,液滴离开喷头后沿相对横向位移正负向两侧依次分布,在相对横向位移达到最大前,相同喷射角度时,先离开喷头的液滴达到的相对横向位移大于后离开的液滴,因此,相对横向位移的波动峰值随时间推移逐渐增大。
(2)液滴的直径越大、初始速度越大,液滴相对横向位移的波动幅值越大,相应的液滴覆盖范围也越大;液滴的喷射角度越大,摇摆运动时液滴相对横向位移的波动幅值越小,相应的液滴覆盖范围也越小。在一定范围内适当减小液滴直径、初始速度或增大喷射角度有利于抑制摇摆运动对液滴运动轨迹的影响。
(3)摇摆条件下,液滴相对横向位移的波动时间间距与摇摆周期相同,波动幅值对应的时刻与摇摆振幅相一致,摇摆振幅越大,相对横向位移的波动幅值越大,但摇摆周期对相对横向位移的波动幅值无明显影响。
