非“图形与几何”领域中开出的“几何之花”
2020-05-06强震球
强震球 中学高级教师,江苏省优秀青年教师,江阴市首批名教师,市兼职教研员。先后获得江阴市、无锡市和江苏省小学数学课堂教学优质课评比一等奖,全国第八届深化小学数学教学改革观摩交流会一等奖第一名。应邀在全国二十多个省(市)、自治区的教学观摩活动中执教观摩课或讲座,深受一线教师好评。
主持多个课题研究,省级课题“小学三年级学习成绩分化的成因及对策研究”获得江苏省精品课题,江苏省教学成果特等奖。
【摘要】“几何直观”主要是指利用图形描述和分析问题,具体来说就是依托、利用图形进行数学的思考和想象。它在本质上是一种通过图形所展开的想象能力,也是一种思维活动。本文强调在“数与代数”及其他非“图形与几何”领域的教学中,研究如何用几何直观的方法培养学生的几何直观表征问题的意识和能力,以及表征之后的顿悟与反思能力,找到解决问题的思路,彰显几何直观的价值,促使学生认识几何直观在数学学习过程中的重要作用,初步学会用几何直观的方法思考和学习数学,真正让“几何之花”开遍学生数学学习的全过程。
【关键词】几何直观 模型 数学素养
一、花开“数轴模型”,变抽象为形象
数学上,数轴是个一维的图,它是一条规定了原点、方向和单位长度的直线。所有有理数都可以用数轴上的点来表示,也可以用数轴来比较两个有理数的大小。数轴是运用几何直观的最佳模型之一,灵活应用数轴,能起到化繁为简、事半功倍的效果。实践中,我们发现数轴能够帮助学生更直观、更深入地认识数,更准确地理解数与数之间的关系,为学生数感的建立起到积极作用。
例如五年级“认识负数”一课中,借助数轴,学生就能很好地从本质上理解正负数的意义,以及“0”的作用。在教学中,教师可以由一个不完整的温度计(没有0的温度计),逐渐转变成半直观半抽象的数轴,最后形成完整的数轴模型。利用数轴可以开阔解题思路,解决诸如表示点的位置、进行数的大小比較等问题,表示正数的点在原点的右边,表示的数越大,这个点到原点的距离也就越远;表示负数的点在原点的左边,这个点到原点的距离越远,则这个负数就越小;0在数轴上是用原点来表示的。在认识负数以前,学生常常认为“0”是最小的数,或者表示“没有”,现在再通过数轴来看数字“0”,学生就能重新认识它的地位和意义了。
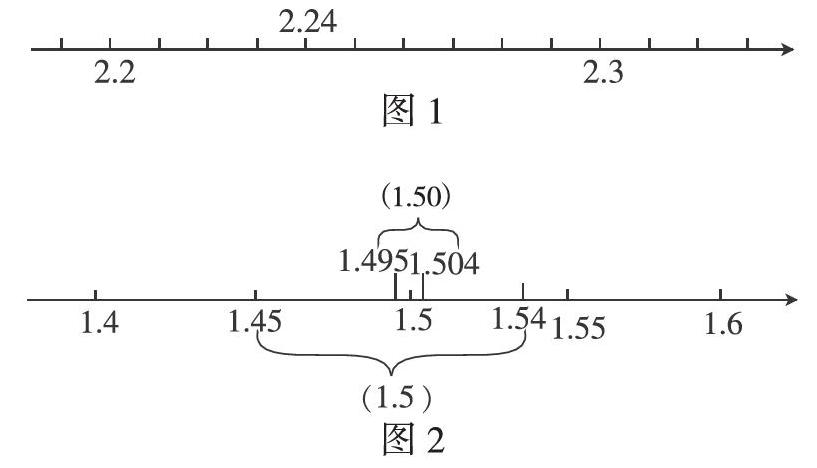
再如,在教学“近似数”的内容时,学生利用数轴就可以直观、形象地理解一个小数的近似数的原理以及精确度的概念。如:“2.24更接近哪一个一位小数?为什么?”有一定数感的学生可能会马上知道结果是2.2,但是能真正理解“为什么是2.2?”的同学并不是很多。于是,教师在这时就请出数轴来帮助学生直观地理解其中的道理。如图1,
经过数轴的帮助,学生能很直观地看出2.24更接近2.2,所以它的近似数是2.2。又如“1.5和1.50都是1.496的近似数,哪一个更精确?为什么?”这个问题是比较有挑战性的,借助数轴来帮助学生理解这个问题就显而易见了。如图2,
从数轴上可以清楚地看到1.5的范围是1.45~1.54,1.50的范围是1.495~1.504。近似数为1.50的范围比大约1.5的范围小,由此可见,1.50更精确,精确度也更高。
二、花开“算式模型”,变复杂为简单
在数学中,算式是指在进行数(或代数式)的计算时所列出的式子,包括数(或代替数的字母)和运算符号(四则运算、乘方、开方、阶乘、排列组合等)两部分。按照计算方法的不同,算式一般分为横式和竖式两种。每一种算式都有着自己固定的模型,而算式中的每一部分彼此间又有着看似简单却密不可分的联系。借助算式模型,以及算式中各部分之间的关系,能有效地帮助学生解决“数与代数”领域中出现的拓展性问题。
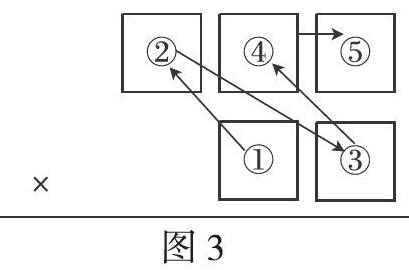
例如,学生在四年级学习了“两位数乘三位数的乘法”后,会有这样的思考:“用1、2、3、4、5这五个数字组成一个两位数和三位数,要使积最大,应是哪两个数?要使积最小呢?”对于一般的学生来说,这个问题的难度很大,还有一部分学生会用口诀“差大积小,差小积大”来解决,但是这句口诀学生真正理解吗?教学中笔者努力尝试用直观的方式来帮助学生解决这个问题。经过尝试和研究,发现利用竖式模型(图3)能便于学生顺利地找到结果。
我们知道,在计算三位数乘两位数的时候,最高位上相乘就能初步确定积的大小。求积的最大值时,首先考虑①、②号位置上的数字相乘的结果要最大,就要选数字4、5,而数字5一定要放在①号位置,因为用5乘三位数的十位和个位,所得的结果比用4乘三位数的十位和个位所得的结果大。接着,考虑④号位置上只能是数字3,因为3乘两位数的结果大。其次,③、⑤位置上放1、2,而数字2一定要放在③号位置上,因为2乘三位数比1乘三位数的结果大。由此,我们也不难发现,将1~5这五个数,按从大到小的顺序,依次填写在①—⑤号位置上(如图3箭头所指),所以结果是431×52的积最大。而求积最小的情况,则与最大值的情况相反,所以结果是245×13的积最小。
再如,五年级有这样一个挑战题:“小马虎计算30.6除以一个数时,由于把除数的小数点向左点错了一位,结果得到12。原来的除数是什么?”解题时很欣喜地看到学生能自主运用直观模型来解决,利用除法算式模型、除法各部分之间的关系以及对与错两次的对比变化,学生呈现了变化的过程,将文字直观化,进而对照直观模型利用倒推等策略顺利地解决这个问题。
三、花开“线段图模型”,变混淆为清晰
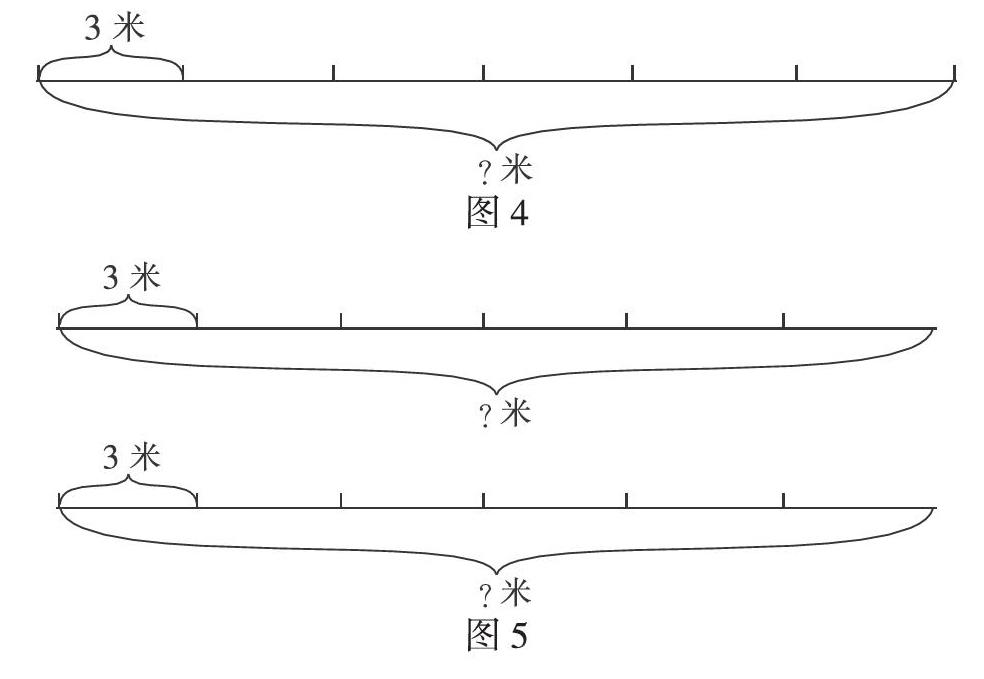
线段图是由几条线段组合在一起,用来表示应用题中的数量关系,帮助学生分析题意、解决问题的一种平面图形。它是从抽象的文字到直观的再创造、再演示的过程。线段图,以其形象、直观的特点,在数学教学中广泛应用。在数学教学中,注重让学生运用线段图这个模型来解决实际问题,能有效地提高学生的自主学习能力,使学生学会学习。例如,在教学四年级“一一间隔规律的实际问题”时,教师出示例题:“一条林荫道上共栽了7棵树,相邻的两棵树相隔3米。林荫道长多少米?”大部分学生看到题目后是茫然的,于是教师着重启发学生思考7棵树是怎么种的。当学生说出某种方法后,引导学生在草稿纸上画出树是怎么种的,讨论得出:用点代表树,用线段代表间隔3米。画出第一个线段图,如图4, 教师随后重点引导学生观察线段图,认清“什么和什么一一间隔排列”“头尾是怎样的情况”,并进一步引发思考“7棵树一定只能这样种吗?”。有了第一个线段图这个初步模型,学生便比较顺利地思考出另外两种情况的线段图,一种是“头尾都不种”,一种是“头种尾不种”或者“头不种尾种”(如图5)。
就这样,三种不同情况的线段图模型就形成了。学生在画图、识图、比图的过程中,逐步强化植树问题中的三种直观模型,为后面解决求林荫道长度的问题奠定基础。之后呈现的兔子排队问题,笔者就放手让学生尝试模仿,直接画出直观图并解答。
四、花开“连线图模型”,变内隐为外显
在小学第一学段数学学习中,连线是学习中常用的一种数学方法,它的价值就在于能有序、不重复、不遗漏地进行数学分析,将隐藏在头脑中的思维过程外显,从而最终找到所求问题的结果。在第二学段的教学中,教师要好好利用连线图的数学价值,将比较复杂的思维过程直观地呈现在连线图中,以便学生更有利地继续展开数学思考,找寻数学规律,解决数学问题。
例如,在教学“搭配的规律”中,为了让学生找到蕴藏在搭配中的规律,教师可以引导学生进行连线,将搭配的过程清晰地表示出来。学生呈现的可以是完整的连线图(如图6),继而教师逐步引导学生过渡到半抽象的连线图(如图7)。
但是不管是哪一种连线图,都要让学生借助连线图明确:每一顶帽子都可以和4个不同的木偶搭配,那么有4种不同的搭配方法。有3顶不同的帽子,那么就有3个4种,也就是3×4=12种不同的搭配方法,进而得出搭配的规律——两种不同类的物体搭配所得的搭配方法数=两种物体的数量相乘。
几何直观是揭示现代数学本质的有力工具,有助于学生形成科学正确的世界观和方法论,而直观模型在培养几何直观的过程中起着重要的桥梁作用。在小学数学教学中,教师合理地运用直观模型能更好地发挥几何直观的教学价值,促进学生更有效地理解抽象的、复杂的、混淆的、内隐的数学内容,从而提高学生的数学素养。
