分层走班语境下数学学科A层教学策略

刘沁桥 许小红

《矩形的判定》是人教版第十八章“平行四边形”第二节的内容。矩形是学生学习的第一种特殊的平行四边形，既要对平行四边形的相关知识进行内化，又要对其在平行四边形基础上所蕴含的特殊性质进行延伸，为后续学习菱形、正方形奠定基础，在教材中具有承上启下的重要作用。根据分层走班A层学生的实际情况，教师设计了以下教学目标：一是引导学生掌握运用矩形的定义和判定定理判定四边形是矩形的方法;二是引导学生经历探索、猜想、证明的过程，逐步发展推理论证的能力;三是学生能应用矩形定义、判定等知识解决简单的证明题和计算题。本节课的教学重点是学生能够理解、证明矩形的判定定理并利用定义和定理进行证明;教学难点是学生灵活运用矩形的性质和判定及其相关结论解决问题。

一、 定向开启环节

在学习了矩形及其相关概念的基础上，教师引导学生回顾关于矩形的知识，提出如下问题：①矩形的定义是什么？②矩形的性质有哪些？这两个问题帮助学生梳理思路，唤醒学生对边、角、对角线的记忆。

采用提问的方式，一方面能够了解学生对旧知识的掌握程度，为新知识的学习做好必要准备;另一方面，在课堂伊始，学生思维还没有进入状态，提问的方式能使他们快速进入思考状态，为新知识的探究做好精神准备。

二、示疑互动环节

第一个环节完成之后，教师要引导学生思考：类比平行四边形的判定定理與其性质之间的关系，能否由矩形的性质判定矩形，然后请学生思考如下两个问题：①“矩形的对角线相等”的逆命题是什么？是真命题吗？②如何调整“对角线相等的四边形是矩形”，使其为真命题？

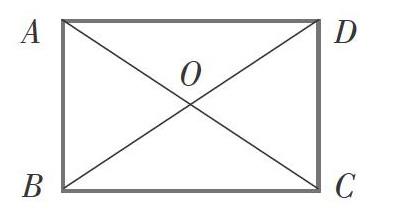
这是由矩形区别于平行四边形的性质猜测矩形的判定，是一种合理的猜测方式，让学生建立这样的思维方式对于发散思维的培养很有必要。实际教学中，教师可请一位表达能力较好的学生将命题翻译为数学证明题的形式，即：如下图，在四边形ABCD中，AC、DB是它的两条对角线，AC=DB，求证四边形ABCD是矩形。

教师可以做两个方面的提示：一是平行四边形的邻角互补，对角相等;二是有一个角是90°的平行四边形是矩形。考虑到A层学生的实际，教师采用了填空的形式归纳，即“     的     是矩形”。这样设计能避免学生归纳时的茫然，使他们得出定理1：“对角线相等的平行四边形是矩形。”

定理2的探究，可以先让学生思考：四个角是直角的四边形是矩形吗？至少有几个角是直角可以判定四边形为矩形？然后，出示以下题目：如下图，已知在四边形ABCD中，∠A=∠B=∠C=90°，求证四边形ABCD是矩形。

由于学生已经有了推断定理1的经验，所以定理2的探究速度可适当加快。教师可以按照“逆命题—判真假—调整猜想—验证—总结”的思路，引导学生自主归纳出“有三个角是直角的四边形是矩形”，并用几何语言表述为：∵四边形ABCD是平行四边形，∠A=∠B=∠C=90°，∴四边形ABCD是矩形。

至此，学生已学习了三种判定矩形的方法（两种判定定理，一种矩形定义）。教师要引导学生进行梳理，对三种判定方法的特点进行归纳：如果是平行四边形，则需证明有一角为直角或对角线相等;如题中未强调平行四边形或者直角较多时，则利用定理2来证明。这样的总结对于A班学生尤为必要，因为他们在平时的学习中缺乏自我总结的习惯，甚至很多学生缺乏主动思考的积极性，所以在总结后紧接着训练其对于解题思路的选择直觉，能在一定程度上调动学生思考的积极性。

三、悟理明法环节

在具体情境中，如何选择更合适的定理解决问题呢？教师设计了以下练习题。

1.在□ABCD中，对角线AC，BD相交于点O，且OA=OD，∠OAD=50°，求∠OAB的度数。

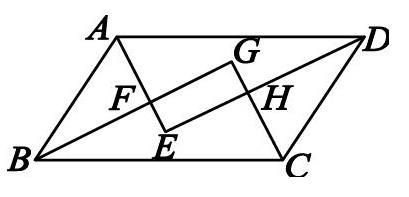
2.如下图，[？ABCD]的四个内角的平分线分别相交于点E，F，G，H。求证：四边形EFGH是矩形。

第1题利用了“对角线相等的四边形是矩形”的判定定理。学生解答之后，教师将题目变为“已知[？ABCD]的对角线AC，BD相交于点O，△AOB是等边三角形，AB=4cm，求这个平行四边形的面积”，引导学生进一步应用定理。第2题可以用“有三个角为直角的四边形是矩形”进行证明。把两题放在一起而不是在每个判定定理之后进行训练，正是在学生初步掌握的数学知识基础上，将知识进行内化的一种训练。选哪一种判定定理来证明？怎么选？这些问题都将促使学生思考定理之间的区别与联系，从而达到内化知识、甄别知识点的目的。

四、入脑融合环节

通过以上学习，学生基本掌握了本节课的知识。教师针对学生易忽略的细节，设计了三类练习题，引导学生进行强化练习。

一类以夯实基础为目标，让学生判断以下说法的正误并说明理由：①有一个角是直角的四边形是矩形;②对角线相等的四边形是矩形;③对角线相等，且有一个角是直角的四边形是矩形;④两组对边分别平行，且对角线相等的四边形是矩形。第二类以梳理知识为目标，请学生小结“今天学了哪些内容”。学生要能总结出“一种学习方法;两个猜想证明;三种判定方法”。第三类以开拓思维为理念，设计开放型题目：任意四边形ABCD四边中点分别为E、F、G、H，添加什么条件能使四边形EFGH为矩形？

三类题目由易到难、由浅入深，既有利于学生巩固知识，又能让他们通过练习获得成就感。

（作者单位：武汉经济技术开发区第一初级中学官士墩校区）

责任编辑  张敏