整理交流 建构整合

郑华

如何提高数学复习的有效性？笔者以小学五年级上册《多边形的面积整理与复习》为例，谈谈个人想法。

一、整理交流，理清知识结构

在复习课中，教师要引导学生对学习过的数学知识进行梳理，要善于抓住学生容易忽略、易错的知识点进行查漏补缺，使学生全面、系统、完整地掌握数学知识和技能。

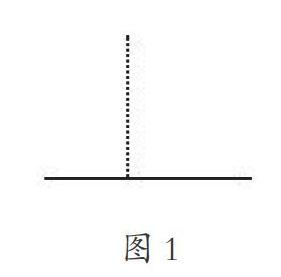
复习《多边形的面积》前，笔者布置前置性作业，要求学生自主整理单元内容。课堂上，为提高学生复习兴趣，笔者首先出示图1，并问学生：“看到这组线段，你能想到哪些学过的平面图形？”学生回答：有平行四边形、三角形、长方形、梯形。

教师用课件出示学生所说图形（如图2）。

师：如果两条线段的长度分别是20cm、15cm，以上图形的面积各是多少？你能尝试着计算一下吗？

生1：平行四边形面积=底×高，所以第一个图形的面积是20×15=300cm2。

生2：三角形面积=底×高÷2，所以第二个图形的面积是20×15÷2=150cm2。

生3：长方形面积=长×宽，所以第三个图形的面积是20×15=300cm2。

生4：梯形面积=（上底+下底）×高÷2，因为不知道上底，所以第四个图形的面积无法计算。

师：这些图形的面积之间有什么联系呢？

生1：我们发现平行四边形面积与长方形面积有联系。我们先画出平行四边形底边上的高，沿着高剪开，可以拼成一个长方形，这个长方形的长实际上就是平行四边形的底，宽实际上就是平行四边形的高，因为长方形面积=长×宽，所以平行四边形面积=底×高。

师：这里的“底×高”有什么要求？

生1：底乘以底边对应的高。

师：平行四边形面积公式的推导其实蕴含着一种数学思想，是什么呢？

生（齐）：转化思想。

生2：平行四边形面积与三角形面积有联系。任何一个平行四边形都可以分成兩个大小完全一样的三角形。因为平行四边形面积=底×高，所以三角形面积=底×高÷2。

师：计算三角形面积时，一定不要忘记什么？

生（齐）：除以2。

师：这些图形之间还有哪些联系？

生4：梯形与平行四边形面积之间有联系。两个大小完全一样的梯形可以拼成一个平行四边形。平行四边形面积=底×高，而平行四边形的底是由梯形的上底和下底组成，所以梯形的面积=（上底+下底）×高÷2。

生5：我们组发现三角形面积与梯形面积也有关系。一个梯形可以分成两个三角形，一个三角形的底是这个梯形的上底，另一个三角形的底是这个梯形的下底，根据三角形面积=底×高÷2，可以推导出梯形的面积=（上底+下底）×高÷2。

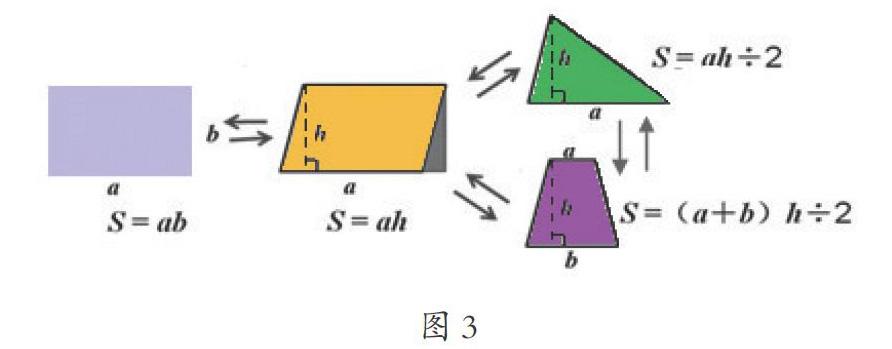
根据学生小组交流的情况，笔者适时板书整理出知识结构图（如图3）：

从一组互相垂直的线段联想到学过的平面图形，有趣并充满挑战，学生通过思考、交流，思维的火花在碰撞，知识结构不断完善、清晰，单元的重难点进一步明确。

二、建构整合，提高思维能力

复习课教学不同于新授课、练习课，它是让学生通过复习，建构知识内在结构，形成一定的数学思想，从而提升思维品质。

《多边形的面积》单元涉及平行四边形、三角形、梯形及组合图形的面积计算，复习课教学中，教师要引导学生进一步明晰面积公式推导过程，探究各种图形的内在联系。

师：图3从右往左画的箭头，表示什么意思？

生1：三角形的面积可以转化成平行四边形面积来计算，梯形面积也可以转化成平行四边形面积。

生2：平行四边形的面积可以转化成长方形的面积。

师：从左往右画的箭头，表示什么意思？

生3：根据长方形面积可以推导出平行四边形面积，根据平行四边形面积可以推导出三角形面积和梯形面积。

师：它们的面积公式是怎么推导出来的呢？

生4：沿着平行四边形的高将平行四边形剪开，把两部分拼起来，所构成的图形就是长方形。因为平行四边形的底相对于长方形的长，高相对于长方形的宽，面积与长方形的面积相等，所以长方形面积=长×宽，平行四边形面积=底×高。

生5：两个完全一样的三角形可以拼成一个平行四边形，三角形的底是平行四边形的底，三角形的高是平行四边形的高，平行四边形面积=底×高，所以三角形面积=底×高÷2。

生6：两个完全一样的梯形可以拼成一个平行四边形，平行四边形的底相对于梯形的上底和下底，平行四边形的高相当于梯形的高，平行四边形面积=底×高，所以梯形面积=（上底+下底）×高÷2。

这样的复习，不仅注重知识点的梳理，而且把握了数学知识点、线、面之间的有机统一，所以复习效果很好。

三、课堂延伸，激发复习动力

复习课教学中，教师要注重知识的“生长点”与“延伸点”，把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系。

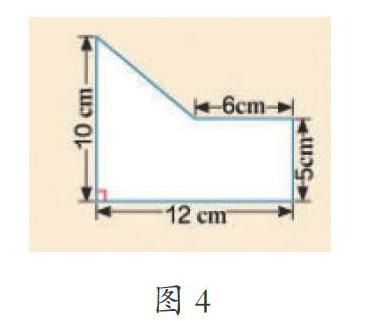
本节课，笔者让学生尝试解答下面的问题：计算下面图形的面积，你能想出几种方法？

学生经过思考，有的把图形分割为三角形和梯形，有的把它分成梯形和长方形，有的把它分成两个三角形，有的把它分成三角形和长方形，有的把它添补成一个长方形，用长方形的面积减去多余的梯形面积求出组合图形的面积，还有的把它添补成梯形，用梯形的面积减去多余的三角形面积计算出组合图形的面积。

这道练习题在打开学生思维的同时，也让他们再次感受到“转化”的数学思想——不管是分割法、割补法还是整体观察法，都是将一个新图形先转化成已知图形再来求面积。

（作者单位：十堰市五堰小学）

责任编辑  张敏