培养学生类比推理能力

刘鹏飞

类比推理是合情推理的重要形式之一，是引发猜想、发现结论的有效途径。教师可以在性质、法则、定律以及几何图形、数形结合教学、解题方法指导教学的过程中，逐步提高学生的类比推理能力。

一、在性质、法则、定律教学中培养

小学数学中有部分内容的性质、法则、定律是相似的。教学中，教师应注重它们之间的联系，引导学生用类比推理的方法来学习。

例如，“异分母分数加减法”本质上的知识是“相同数位上的数，才能直接相加减”这一计算法则。学生在学习整数、小数、同分母分数加减法时，已经形成了这种计算认识，积累了这种计算经验。因此，教学时可以先设计一组整数、小数、同分母分数加减法练习，如：

笔者引导学生归纳出计算过程背后隐含的共同核心要素——相同数位上的数，才能直接相加减。学生受这个计算原理的启发，就能类比尝试，将异分母分数转化成同分母分数，再相加减。归纳出异分母分数加减法的法则后，再次进行新旧知识的对比，凸显出此类计算的共同点，强化新旧知识之间的本质联系。

还有许多运算定律之间也有十分密切的联系，比如，整数加减法运算定律对小数、分数同样适用，加法结合律、交换律对于乘法也同样适用。这一系列的类比教学活动，能促进学生对知识的深刻理解，帮助他们构建比较完善的知识结构。

二、在几何图形的教学中培养

几何图形之间也有许多相似之处，在学习新的几何图形时，教师应让学生将其与已学过的、熟悉的图形进行比较，猜测新图形可能具有的性质、结构，建立起新旧图形间的联系。几何图形结构的类比主要有三种形式：平面图形间的类比、立体图形间的类比，平面图形与立体图形的类比。

1.平面图形间的类比。在教学正方形的面积计算公式时，我们可以通过长方形与正方形之间的关系以及长方形的面积计算公式，类比出正方形的面积计算公式：

除此之外，小学数学中的其他平面图形，如平行四边形、三角形、梯形、圆的周长等公式，都可以由已有图形推导出来。教师应梳理它们之间的推导过程，帮助学生建立系统化思维。

2.立体图形间的类比。教学圆柱的体积公式时，我们可以根据等积变形后长方体与原圆柱体之间的关系以及长方体的体积计算公式，类比推出圆柱的体积计算公式：

此外，小学数学中的其他立体图形之间的性质和结构也有密切的联系。比如，长方体的体积公式是通过体积单位直接计量而抽象出来的，正方体的体积公式是根据正方体和长方体的关系类比推导出来的，圆锥的体积公式是利用等底等高的圆锥和圆柱的关系，通过实验推导出来的。

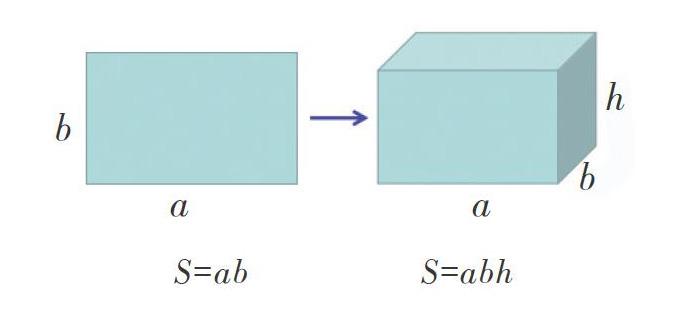
3.平面图形与立体图形的类比。平面图形的边与立体图形的面、平面图形的面积与立体图形的体积之间以及平面图形的面积公式推导方法与立体图形的体积公式推导方法之间都可以进行类比。比如，长方形的面积=長×宽，长方体的体积=长×宽×高：

同时，圆的面积公式的推导方法是将圆平均分成若干等份剪开后拼成近似的长方形，通过长方形面积计算公式推导出来的。圆柱体体积公式的推导方法也是将圆柱的底面平均分成若干等份切开后拼成近似的长方体，根据长方体的体积公式推导出来的。

三、在数形结合教学中培养

数与形是数学研究的两个对象，借助图形描述数式，利用数式解释图形，这样的数形类比，能够启迪思路，发现规律，培养学生的创造性思维。例如，计算“1+3+5+7+9+11+13=（  ）”时，笔者先让学生尝试计算，然后引导学生观察图形，发现规律，最后再利用规律，简便计算（如下图）。

这样的解题过程，将数转换成形，学生受到图形的启发，进行数形类比，能够发现“从1开始，连续奇数相加的和，等于奇数个数的平方”这一数学规律，最后利用发现的规律，简便地算出得数。

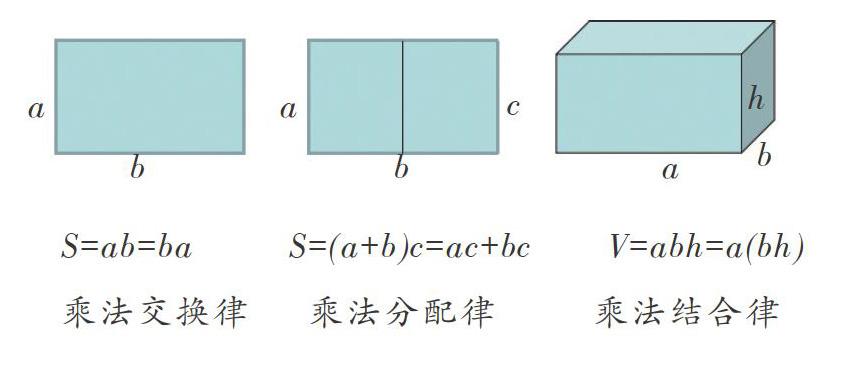
在教学中，有些比较抽象、难以理解的内容还可以和直观形象、易于理解的图形之间进行类比，两者之间可以互相解释，加深学生对这些内容的理解。比如，乘法交换律、分配律、结合律可以和下面图形的面积、体积进行类比：

四、在解题方法指导过程中培养

教学中，教师应注重对解题方法相似的题目的数量关系进行梳理、类比，使学生弄清它们之间的联系，加深对解题方法的理解。

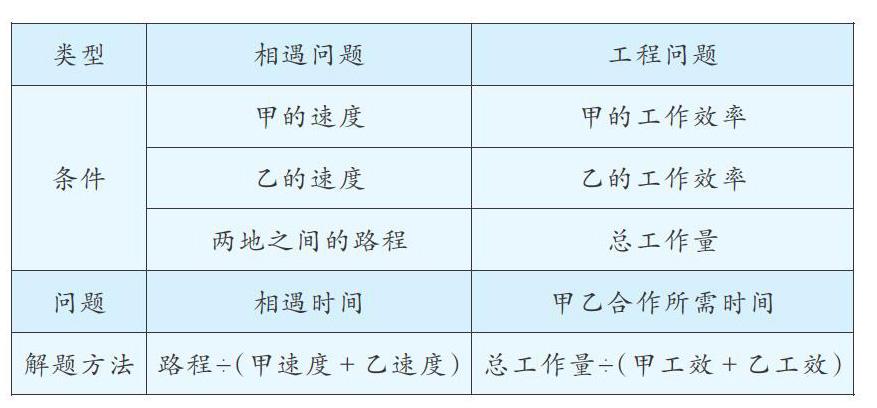
比如，相遇问题和工程问题的解题方法十分相似，教师可对这两类问题进行类比：[类型 相遇问题 工程问题 条件 甲的速度 甲的工作效率 乙的速度 乙的工作效率 两地之间的路程 总工作量 问题 相遇时间 甲乙合作所需时间 解题方法 路程÷（甲速度+乙速度） 总工作量÷（甲工效+乙工效） ]在解答较复杂的、难理解的题目时，教师可引导学生与同类型的基本题目进行类比。由于较复杂的题目中已知条件的本质特征具有隐蔽性，常常造成学生思维受阻。遇到这种情况，教师可引导学生把复杂题与同类型的基本题类比，揭示其结构特征，化难为易。比如，学生解答应用题“一匹布料用来做上衣可做30件，做裤子可做40条，现在用这匹布做了20件上衣后，剩下的布料还可以做多少条裤子”时，可能刚开始会没有思路，觉得没见过这类型的题目。如果教师引导学生和已学过的分数工程问题“一项工程，甲队单独做要10天完成，乙队单独做要12天完成。现在由甲队先单独做3天，剩下的任务由乙队完成，乙队还要做几天才能完成这项工程？”相类比，学生就会茅塞顿开。

在学生掌握了某一种类型题目的解题方法后，教师也可设计一些变式题目让学生来比较、分析，加深对解题方法本质的理解，培养学生的类比推理能力。

（作者单位：武汉市东湖风景区华侨城小学）

责任编辑  张敏