Dynamic responses of a piezoelectric cantilever plate under high-low excitations

Xiangying Guo · Shuaibo Wang · Lin Sun · Dongxing Cao

Abstract In this paper, the nonlinear dynamic responses of a piezoelectric cantilever plate near the first-order and second-order natural frequencies under the action of electromechanical coupling are studied by experiments and finite element (FE) methods. The influence of different excitation frequencies on the dynamical characteristics of piezoelectric cantilever plates is analyzed with the fixed excitation amplitude. First, an experimental setup is built, including a carbon fiber cantilever plate attached to a macro fiber composite (MFC) sheet. Then, the electromechanical coupling excitations are subjected to the plate with different frequencies, which are chosen near the first and second-order natural frequencies of the plate. The piezoelectric cantilever plate has periodical motions under a lower frequency excitation, and the motions of the plate become more complex after another high frequency excitation added in the physical field. The experimental results show that the motion of the piezoelectric cantilever plate changes from stable to unstable with high-low coupled resonant frequencies. At last, the FE study is carried out to compare and verify the experimental results and the effects of isotropic and orthotropic materials on the accuracy of natural frequencies results are also compared.

Keywords Macro fiber composite · Piezoelectric cantilever plate · Dynamics · Electromechanical coupling

1 Introduction

With the development of smart materials, more and more intelligent materials are applied in aerospace, civil engineering and mechanical engineering fields [1-4]. Macro fiber composite (MFC) is a new type of piezoelectric intelligent material and has many advantages, such as large driving torque, good actuation performance, fast responses and easy control and so on. Featuring its inverse piezoelectric effect, MFC has a good application prospect in the shape control [5-7] and vibration control [8-10] of the morphing wings in the aerospace field.

In recent years, many scholars have not only studied the free vibration characteristics of shell structure [11, 12], but also investigated the dynamic behavior of piezoelectric intelligent structures. Wankhade and Bajoria [13] analyzed the vibration characteristics of piezoelectric coupling plates under coupled electromechanical loading by the finite element (FE) method and investigated the effects of geometry and boundary conditions on the vibration characteristics of piezoelectric ceramic plates. Narita et al. [14] analyzed the relationship between the nonlinear bending behavior of piezoelectric laminated actuators and the parameters of large electric excitation. Shindo et al. [15] present the nonlinear bending behavior caused by domain wall motion in a functionally graded piezoelectric actuator under alternating electric fields. Parashar and Wagner [16] modeled the nonlinear behavior of piezoceramics using higher order (quadratic and cubic) conservative and dissipative terms in the constitutive equations. Amr et al. [17] investigated the static and dynamic characteristics of piezoelectric actuators and compared the bending deflection of piezoelectric actuators subjected to different voltages. Jia et al. [18] built up a dynamic multiphysics FE model, in which representative environment vibration data were utilized to dynamically excite a piezoelectric MFC on carbon fiber composite beam. Lee and Inman [19] discussed the nonlinear vibration characteristic of rectangular piezoelectric bistable laminates. Syta et al. [20] experimentally investigated the dynamic responses of an energy harvesting device based on a bistable laminate.

In practical applications, piezoelectric intelligent structures are excited by a variety of external excitations, not only by different discrete excitation, but also by a variety of coupled excitations. Kundu and Nemade [21] built a bimorph piezoelectric cantilever model with masses at the end and also obtained resonant frequency, displacement of end mass and generated voltage across resistive loads. Li et al. [22] investigated the nonlinear dynamic behavior of corrugated graphene/piezoelectric laminated structures under electromechanical coupling loads. Lumentut and Howard [23, 24] modeled an electromechanical piezoelectric bimorph beam with tip mass under transversal and longitudinal excitations for power harvesting. Chen et al. [25] presented a new modeling and analysis approach for the bending characteristics of hybrid thermo-piezoelectric micro actuators. Pourrostami et al. [26] developed an analytical model for a hybrid thermos-piezoelectric micro actuator. Kumar and Chakraborty [27] applied a micromechanical model based on strength of materials approach for evaluation of coupled thermos-electro-mechanically coefficients of piezoelectric fiber reinforced composites. Rakotondrabe and Ivan [28] presented a new hybrid microactuator based on the combination of piezoelectric and thermal effects. The proposed actuator could perform both a high-stroke coarse positioning and high-resolution fine positioning.

The effect of high-frequency excitation on dynamic systems is not only significant in the case of the corresponding high-frequency response, but also in the modification of the low-frequency mode of systems [29, 30]. Blekhman and Sorokin [31] proposed an explanation for the stochastic resonance phenomenon, which occurred in a system excited by two (or more) vastly different frequencies forces. Qian and Yan [32] investigated different dynamic behaviors of a coupling Duffing system subject to periodic excitations in high-low frequencies excitation. Han and Bi [33] considered the external forcing as a control parameter and studied its influence on the controlled Duffing’s system, and developed two strategies to account the bursting oscillations.

There are lots of research papers related on the dynamical behavior of piezoelectric cantilever plate by theoretical method. This paper is focused on the experiment way to discuss the effects of high-low excitations on the dynamical behavior of the MFC structures and the results express some interesting phenomenon of the responses for these MFC structures. Firstly, an experimental platform is established to investigate the dynamic characteristics of a piezoelectric cantilever plate under different kinds of excitations. Then, the FE model of piezoelectric cantilever plate is established by COMSOL Multiphasic. In FE analysis, the first two natural frequencies and mode shapes of the structure are obtained. Time dependent analysis is employed to analyze the influence of difference excitation frequencies on the vibration responses of a cantilever plate and compared with those experimental results. Meanwhile, the effects of isotropic and orthotropic materials on the accuracy of natural frequencies results are compared.

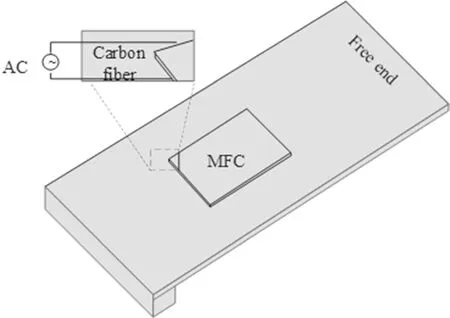
Fig. 1 Piezoelectric cantilever model. AC: alternating current

Table 1 Properties of MFC

2 Experimental setup

Design a carbon fiber cantilever plate with MFC sheet on the surface of the plate as the mechanical model shown in Fig. 1. The carbon fiber reinforced composite plate has a size of 300 mm × 100 mm × 0.3 mm and is an orthotropic material. An MFC sheet (M8557-P1, 85 mm × 57 mm × 0.3 mm) is bonded to the upper surface of the carbon fiber plate. The physical parameters of MFC and carbon fiber reinforced composites are shown in Tables 1 and 2.

The experimental platform and process are shown in Figs. 2 and 3, respectively. The piezoelectric cantilever plate (8) is fixed to the JZK-5T electric shaker (7) by a fixture (6). The YE1311 signal generator (2) is applied to supply the original sinusoidal excitation signal, and then the signal is transmitted to the shaker through the YE5874 power amplifier (3), and finally the piezoelectric cantilever plate vibrates in the lateral direction. The MFC’s driver works similarly to the shaker. The Agilent signal generator (5) produces the original harmonic signal, which could be transmitted to the MFC voltage amplifier (4) for output high voltage. Then, the high voltage input to the positive and negative terminals of the MFC through wires. The displacements of the free end for the piezoelectric cantilever plate are acquired by the LK-G5000 laser displacement detector (10).

Table 2 Properties of carbon fiber composites

The resonance caused by external forces is often happened in the region of low frequencies. Therefore, the first two modes of the piezoelectric cantilever plate are analyzed here. The sweeping frequency method is applied to obtain the resonance frequencies through measuring the vibration amplitudes of the plate. The range of sweeping frequency is 1-50 Hz with step 1 Hz, and the amplitude-frequency diagram is obtained as Fig. 4, which shows that the first two frequencies of the piezoelectric cantilever plate are respectively near 4 Hz and 24 Hz. In order to study the effect of high-low frequency excitations on the vibration of piezoelectric cantilever plate in the electromechanical coupling field, the experimental research is divided into two steps: the first one is to obtain the dynamic responses of the piezoelectric cantilever plate under a single external excitation (electric or force fields), and the second step is to analyze the responses of the piezoelectric cantilever plate in high-low electromechanical coupling fields. The amplitudes of all excitations are fixed in the process and the effects of the high-low excitation frequencies on the vibration of the piezoelectric cantilever are considered.

Fig. 2 Experiment platform. a, b Experimental equipment. 1: LK-navigator, 2: signal generator, 3: power amplifier, 4: high voltage amplifier, 5: Agilent signal generator, 6: fixture, 7: shaker, 8: piezoelectric cantilever, 9: LK-G controller, 10: laser displacement detector

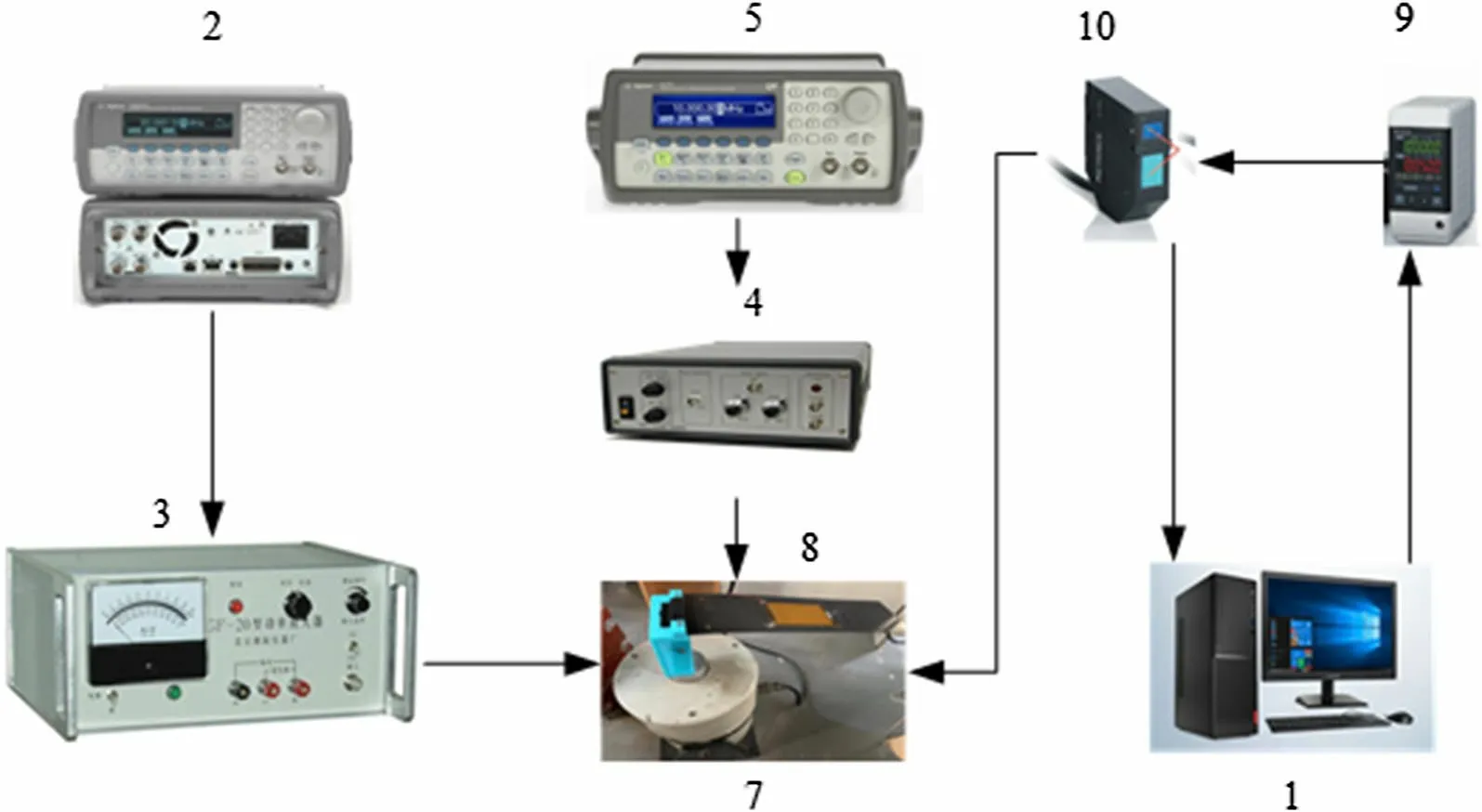
Fig. 3 Experimental process

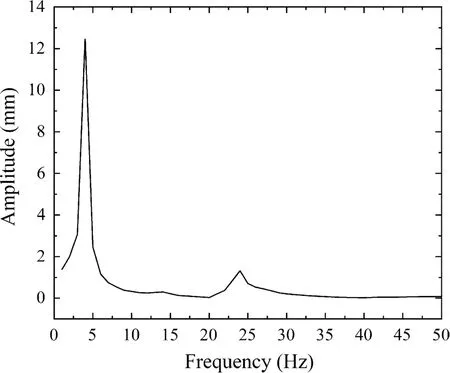
Fig. 4 Amplitude-frequency diagram

2.1 Dynamic responses of the cantilever plate under single external excitation

2.1.1 Only lateral displacement excitation applied to MFC

Firstly, transversal sinusoidal displacement excitation is applied to the fixed end of piezoelectric cantilever plate, where the excitation frequencies are 4 Hz and 24 Hz and the amplitude keeps 1 V. This voltage signal is generated by the signal generator and can be adjusted in amplitude. The laser displacement sensor collects the free-range displacement signal of the plate. The waveform and phase diagrams are obtained as shown in Fig. 5 to illustrate the dynamic characteristics of the piezoelectric cantilever plate under each above frequency. It can be seen from Fig. 5 that the piezoelectric cantilever plate exhibits periodic motion under the lateral displacement excitation of 4 Hz and 24 Hz separately, and the vibration amplitude at 24 Hz is significantly lower than that of 4 Hz.

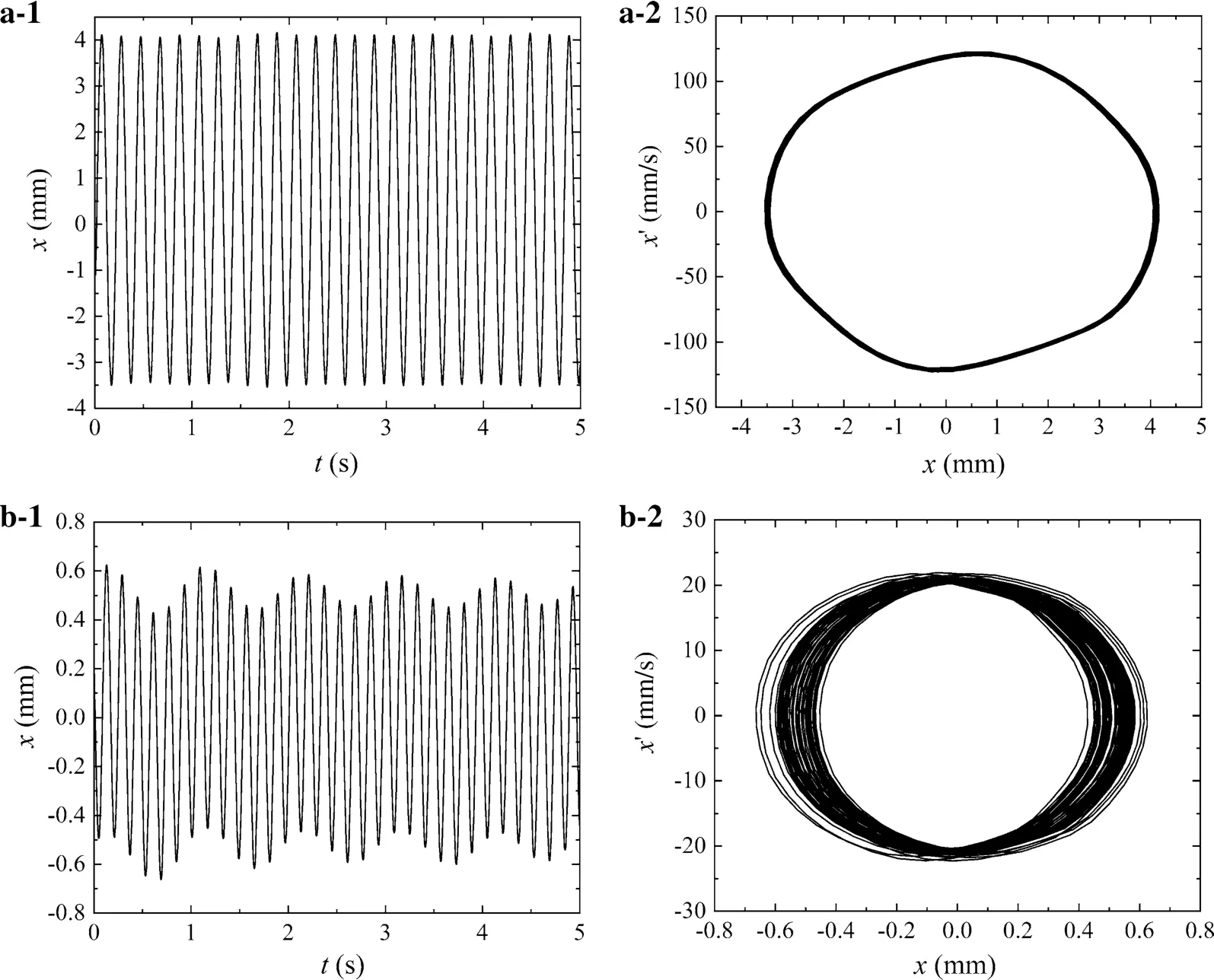
Fig. 5 Waveforms and phase diagrams of piezoelectric cantilever plate under different frequency displacement excitations. a 4 Hz, b 24 Hz

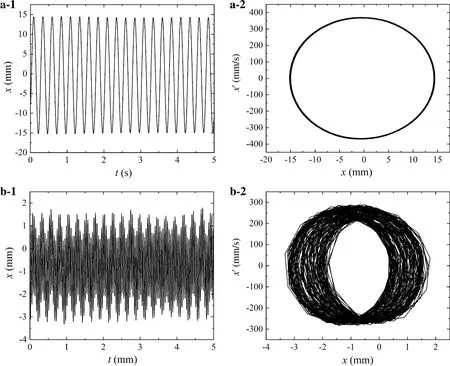
Fig. 6 Waveforms and Phase diagrams of piezoelectric cantilever plate under different frequency AC excitations. a 4 Hz, b 24 Hz

2.1.2 Only AC power applied to MFC

Then, only AC power is applied to the MFC with 1v and the frequencies of AC power are also chosen as 4 Hz and 24 Hz, respectively. The free end displacements of the cantilever plate are measured by a laser displacement detector as shown in Fig. 6.

From Fig. 6, it is found that the cantilever plate exhibits periodic motion when the frequency of AC power equals to 4 Hz and there exists quasi-periodic motions near the second-order natural frequency of the plate. Moreover, the amplitudes of the plate in 4 Hz are much higher than that of plate in 24 Hz from the waveform diagrams.

2.2 Dynamic responses in electromechanical coupling fields

The effects of frequencies of the electromechanical coupling excitations are analyzed on the vibration of a piezoelectric cantilever plate. The frequencies of two coupled excitations are divided into three combination cases, which include low-low, high-high and high-low frequencies. Waveforms and phase diagrams of various combinations are shown in Fig. 7.

Figure 7a shows that the piezoelectric cantilever plate exhibits a “beat” phenomenon and the maximum amplitude is 13 mm, when the frequencies of both the transversal excitation and AC power are almost 4 Hz. The “beat” phenomenon disappears as the frequencies of electromechanical coupling excitations are chosen as 4 Hz and 24 Hz and vice versa. The cantilever plate exhibits a quasi-periodic motion, which shown in Fig. 7b, c.

When the frequencies of transversal excitation and the AC are both near 24 Hz, a “beat” phenomenon occurs again, as shown in Fig. 7d. From the waveform diagram of Fig. 7, it can be found that the maximum amplitude of the piezoelectric cantilever plate is not simply the addition or subtraction of the two coupled excitations, which is also related to the initial phase of the coupled excitations. When the initial phases of coupled excitations are the same, the amplitude of the plate reaches its maximum. If the phases of these excitations are totally opposite, the amplitude of the plate gets its minimum.

Fig. 7 Waveform and phase diagrams of the plate under two excitations. a Shaker 4 Hz and AC 4 Hz, b shaker 4 Hz and AC 24 Hz, c shaker 24 Hz and AC 4 Hz, d shaker 24 Hz and AC 24 Hz

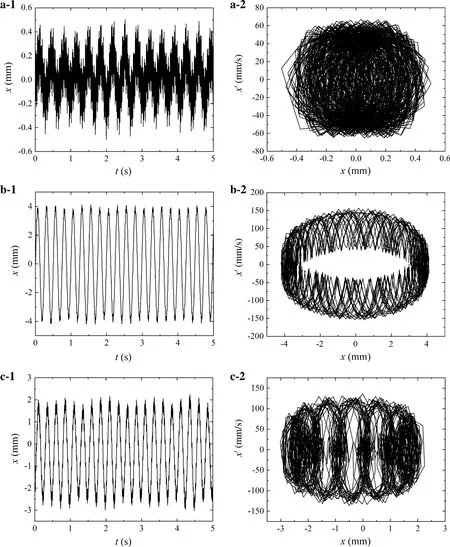
Fig. 8 Waveform and phase diagrams of the plate under two excitations. a Shaker 52 Hz, b shaker 4 Hz and AC 52 Hz, c shaker 52 Hz and AC 4 Hz

2.3 Responses of the plate under higher frequency excitations

Next, the dynamic behaviors of the piezoelectric cantilever plate are analyzed experimentally under the another high-low coupled excitations of 4 Hz and 52 Hz, which are near the first and third-order natural frequencies of the plate. The different motions of the piezoelectric cantilever plate are obtained as shown in Fig. 8. There exists chaotic motion of the plate with single 52 Hz excitation as shown in Fig. 8a, and then the motion of the plate varies from unstable to stable when another excitation of 4 Hz is added to the system shown in Fig. 8b, c. Compared with the response of the cantilever plate under the electromechanical coupling excitation of 4 Hz and 24 Hz, it can be concluded that the motion of the piezoelectric cantilever plate changes from quasi-period to chaos with the increase of resonance frequency. When frequencies of the transveral excitation and the AC are 4 Hz and 52 Hz, the piezoelectric cantilever plate exhibits quasi-periodic motion; when the frequencies of two excitation changed, chaotic motion of the plate will occurs.

Table 3 Comparison of modal analysis results

3 FE analysis

3.1 Eigenfrequency analysis

In order to verify experimental results, the vibration responses of the piezoelectric cantilever plate under the electromechanical coupling field are also investigated by the FE method. In COMSOL Multiphysics, the physical field interface of the piezoelectric device is applied, and the solid mechanics and the electrostatic module are combined to establish an electromechanical coupling model of the plate. The modal and dynamic responses of the structure are analyzed by eigenfrequency and time dependent, respectively.

To verify the accuracy of the analyzed model, the simulation results of isotropic and orthotropic material are selected and compared with the previous experimental results, which show that orthotropic type of the material match the experimental models well and the compared frequencies are shown in Table 3. It is found from Fig. 9 that the first two modal shapes of the plate are curved, however the bending position is different, such as the first modal shape is bent near the fixed end and the second is near the free end, relatively.

3.2 Dynamic responses of the piezoelectric cantilever plate in FE method

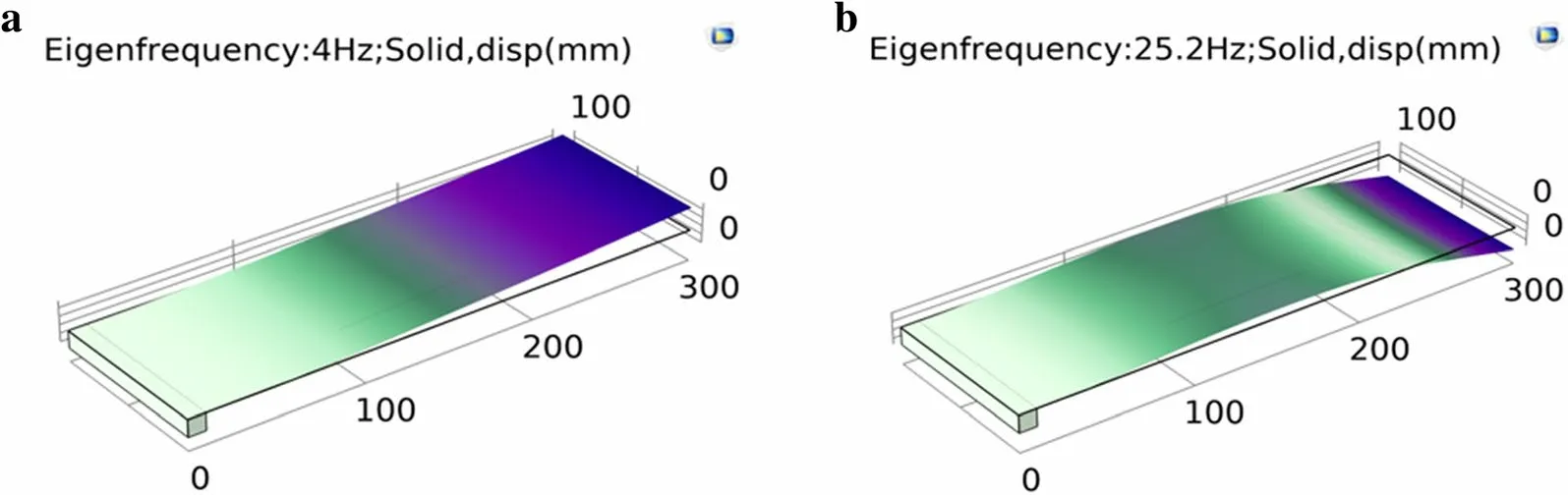
Fig. 9 First two modal shapes of the piezoelectric cantilever. a First-order mode, b second-order mode (unit: mm)

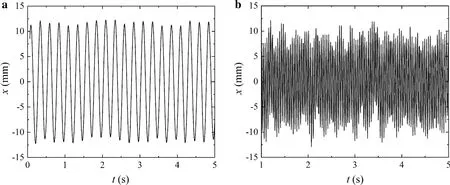
Fig. 10 Waveform diagrams of piezoelectric cantilever under transversal excitation. a 4 Hz, b 25.2 Hz

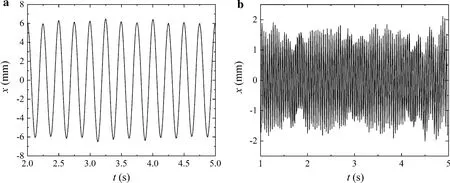
Fig. 11 Waveform diagrams of piezoelectric cantilever under AC. a 4 Hz, b 25.2 Hz

The FE calculation of the dynamic responses of the piezoelectric cantilever plate in electromechanical coupling field keeps mainly consistent with the experimental process. The waveform diagrams of the piezoelectric cantilever plate are obtained as Figs. 10 and 11 by FE analysis under a single excitation are as follows. It is also found the response of the plate is stable in the excitation of 4 Hz and becomes unstable with the high frequency of 25.2 Hz, which are the same as the experimental results. In order to reduce the length of the article, only the waveform diagram are present here for comparing the analyzed results with the experimental results subjected to the same excitation. Since the frequencies of transversal excitation and the AC power cannot completely equal under the experimental conditions, the angular frequencies of these two excitations are set a certain deviation to match the experiment.

Figure 12 shows good agreement of the results between FE simulation and experimental results, such as the beat phenomenon are happened both in Figs. 7a-1, d-1 and 12a, d, quasi-periodic motion of the plate can be found both in Figs. 7b-1, c-1 and 12b, c when the frequencies of transversal excitation and the AC power are equal to the first two natural frequencies, respectively. Chaos is also shown with the coupled high-low frequency excitations both in Figs. 8c-1 and 12f. The amplitude of the piezoelectric cantilever plate will decrease with the coupled of both higher frequency of 52 Hz and low one of 4 Hz, however, the motion of plate becomes complicated and varies from stable to unstable.

4 Conclusions

In this paper, the nonlinear responses of a piezoelectric cantilever plate subject to electromechanical coupling excitation of high-low frequency are investigated experimentally. To verify the correctness of the experiment, the FE model of the piezoelectric cantilever plate under same coupled excitations is established based on COMSOL Multiphysics. The influence of high-low frequencies on the vibration of the piezoelectric cantilever plate is analyzed and compared with the experimental results. Some results are obtained as follows.

1) The motion of the piezoelectric cantilever plate varies from period to chaos with increasing of resonance frequency under a single external excitation.

2) The maximum amplitude of the plate decreases and the motion tend to be stable when the high one of high-low frequencies of the excitations becomes higher. In this paper, the change is adjusted from 25.2 to 52 Hz, which is near the second and third-order natural frequencies of the plate.

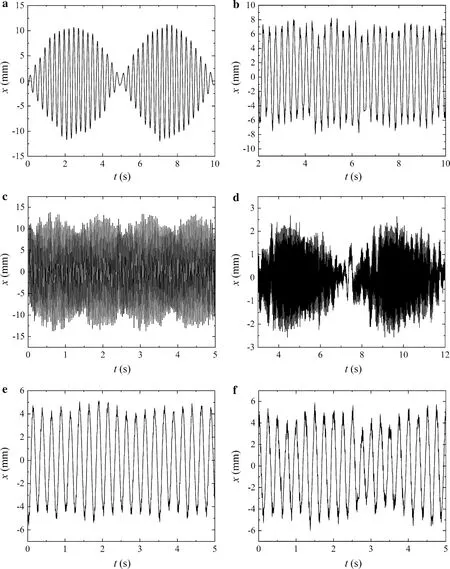
Fig. 12 Waveform diagrams of piezoelectric cantilever under two excitations. a Shaker 4 Hz and AC 4 Hz, b shaker 4 Hz and AC 25.2 Hz, c shaker 25.2 Hz and AC 4 Hz, d shaker 25.2 Hz and AC 25.2 Hz, e shaker 4 Hz and AC 52 Hz, f shaker 52 Hz and AC 4 Hz

3) The piezoelectric cantilever plate appears “beat” phenomenon when the frequency of the two external excitations are same and near to the first or the second-order natural frequency, and this phenomenon disappears with the great difference in the value of two frequencies.

AcknowledgementsThe authors gratefully acknowledge the support of the National Natural Science Foundation of China (Grants 11572006 and 11772010), the funding project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHRIHLB).