Transient growth in turbulent particle-laden channel flow

Yang Song·Chunxiao Xu·Weixi Huang·Lili Wang

Abstract Linear transient growth of optimal perturbations in particle-laden turbulent channel flow is investigated in this work. The problem is formulated in the framework of a Eulerian-Eulerian approach,employing two-way coupling between fine particles and fluid flow. The model is first validated in laminar cases, after which the transient growth of coherent perturbations in turbulent channel flow is investigated, where the mean particle concentration distribution is obtained by direct numerical simulation. It is shown that the optimal small-scale structures for particles are streamwise streaks just below the optimal streamwise velocity streaks,as was previously found in numerical simulations of particle-laden channel flow.This indicates that the optimal growth of perturbations is a dominant mechanism for the distribution of particles in the near-wall region.The current study also considers the transient growth of small-and large-scale perturbations at relatively high Reynolds numbers,which reveals that the optimal large-scale structures for particles are in the near-wall region while the optimal large-scale structures for fluid enter the outer region.

Keywords Optimal transient growth·Wall turbulence·Coherent structures·Particle-laden turbulence

1 Introduction

The motions of particles dispersed in turbulent flow exist widely in nature and industry,such as sandstorms,fluidized beds and combustion chamber flows. As a matter of fact,most of these motions are high-Reynolds-number turbulent flow.Therefore,it is very important to understand how particles can be influenced by turbulent flow,especially at high Reynolds numbers. Over the past several years, numerical simulation techniques for particle-laden flow have been greatly improved.However,the computational cost is still too large to model the motions of particles in turbulence.Therefore,theoretical investigations offer another way to explain the dispersion and deposition of particles in turbulent flow,and can provide a fundamental understanding of numerical simulations and experiments.

Theoretical studies are performed mostly within the framework described by Saffman[1],who considered a dusty gas model with Stokesian particles having negligible volume fraction.In this investigation, it was found that fine dust destabilized fluid flow,while coarse dust had a stabilizing effect.The dusty gas model is a kind of one-way coupling approach,in which the action of particles on fluids is neglected. As a premise, the relaxation time of particles should be sufficiently small relative to the characteristic time for fluids.However, such a basic postulate is not widely established in real physical problems. Hence, it is necessary to involve complex interaction between particles and fluids in theoretical investigations.

Particle-fluid interaction was taken into consideration in the review article by Balachandar and Eaton [2], in which the computational methodology of the multiphase flow is fully classified and discussed. When the particle number density is large, a four-way coupling approach [3] is necessary.One-way or two-way coupling could be utilized only if the particle number density were small enough. When considering one-way or two-way coupling, the computational approaches should differ according to the ratio of the characteristic time of the dispersed phase to the characteristic time of the carrier phase. As the time ratio increases,the proper approaches are the dusty gas model [1], equilibrium Eulerian method[4],Eulerian-Eulerian method[5],Lagrangian point-particle method [6] and fully resolved method[7]in turn.As the complexity of the computational model increases, the computational cost of these methods also sharply increases.

For theoretical investigations,it is always too complicated to involve intricately detailed interactions between particles and fluids.A widely used approach is the Eulerian-Eulerian method. For example, Klinkenberg et al. [8] performed non-modal instability analysis using the Eulerian-Eulerian method to analyze the instability of particle-laden laminar flow. In their model, the interaction between particles and fluids is modeled only by Stokes drag,and the particle concentration in the base flow is uniform. They proved that the stabilization of dusty flow is strongly dependent on the Stokes number. As the Stokes number increases, the particle velocity perturbations can undergo significant growth because of the lack of dissipation. Similarly, Boronin and Osiptsov[9]considered the non-modal instability of particleladen laminar flow with a non-uniform particle concentration by the equilibrium Eulerian approach.In addition to the trivial conclusion, they found that the particle concentration distribution of base flow has an obvious influence on the stabilization of the dusty flow.

As we know, non-modal analysis has long represented a major method for theoretical investigations in laminar flow.On the another hand, this method also began to be widely used for analyzing turbulent flow after the pioneer study by Butler and Farrell[10],in which they elaborated the so-called optimal transient growth of perturbations under a turbulent mean flow profile.The optimal structures obtained by their method are the streaks and streamwise rolls with a spacing of 100 δν,which are very similar to the near-wall coherent structures observed in experiments [11] and numerical simulations[12]. From a dynamical perspective, Hamilton et al. [13]showed that the coherent structures in the near-wall region can self-sustain, and the optimal transient growth seems to be a dominant mechanism for the formation of streaks.This is very meaningful for understanding the dynamics of coherent structures in the near-wall region and controlling the wall turbulence by suppressing the production of these coherent structures [14]. Many studies have already investigated the control schemes of wall turbulence. An example is the socalled opposition feedback control, which can suppress the streamwise vortices by imposing blowing and suction at walls in opposition to the velocity detected a small distance away from the wall[15,16].For numerical simulations and theoretical investigations,the opposition control scheme is easy to formulate and compute. A study by Lim and Kim [17]investigated opposition control by optimal transient growth analysis following Butler and Farrell[10].The authors found that the energy amplification of small-scale perturbations was notably decreased as a result of the control. The optimal detection position predicted by their linear model was the same as that obtained by direct numerical simulations[16]. However, the control performance of opposition control rapidly declined as the Reynolds number increased[18].This diminished control performance is believed to be due to the appearance of large-scale coherent structures in the outer region,which are difficult to suppress by opposition control[19,20].

Although optimal transient growth and its control in turbulent flow has been fully investigated, there is still little research concerning the optimal transient growth in particleladen turbulent flow. In direct numerical simulation (DNS)and large-eddy simulation (LES) [21,22], however, it is already known that particle concentration is significantly influenced by flow structure, especially in the near-wall region,indicating that particle-fluid interaction is important in the near-wall region,where a linear mechanism plays an important role in the dynamics of fluids and particles.

In this paper, optimal transient growth in particle-laden turbulent channel flow is investigated. Here, a Eulerian-Eulerian approach is employed to establish the mathematical formulation. The paper is organized as follows. In Sect. 2,mathematical formulations for the particle-laden turbulent channel flow are given, and the simplification of a mathematical model is also discussed.Model validation is shown in Sect.3.1,where particle-laden laminar flow is considered.In Sect.3.2,optimal transient growth of small-scale perturbations in turbulent flow at Reτ=180 is analyzed,after which the optimal transient growth of both small- and large-scale perturbations at Reτ= 1000 is investigated in Sect. 3.3.Finally,conclusions are drawn and discussion is provided in Sect.4.

2 Mathematical formulations

In this section,mathematical formulations are derived using a Eulerian-Eulerian approach.The physics problem investigated here is the particle-laden turbulent channel flow with Stokesian particles,which is statistically homogeneous in the streamwise(x)and the spanwise(z)directions.The motion of the flow is governed by the following equations:

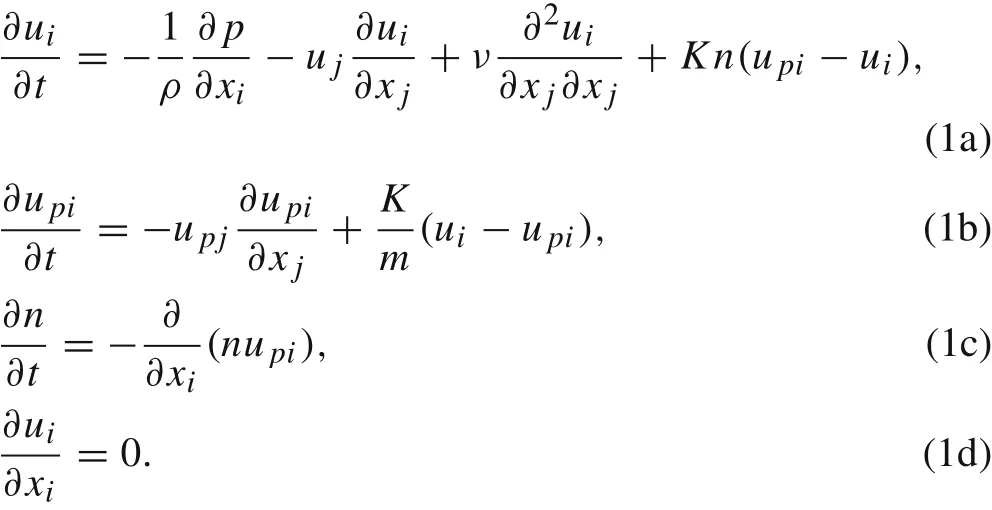
Here,ui,u pi and p represent fluid velocity,particle velocity andpressure,respectively.n is the number density of particles whose mass are the same m.K is the drag coefficient of particles.In the following study,the drag coefficient is defined as K =6μπr (r is the radius of particles).In this instance,the ratio of the relaxation time of particles to the characteristic time of fluids is assumed to be sufficiently small.

2.1 Mean flow

First,the averaged equations of particle-laden turbulent mean flow should be considered, and the properties of the mean flow are studied. For particle-laden channel flow with particles of small Stokes numbers, it is reasonable to assume that the mean velocities of fluids and particles are steady and parallel to walls.Hence,the mean fluid velocity can be expressed as U = Uexwith U = U(y), the mean particle velocity as Up= Upexwith Up= Up(y), and the mean particle number density as N = N(y). Then any physical quantities can be decomposed into mean quantities and turbulent fluctuations[denoted by ˜(·)],i.e.,Ui+ ˜ui,Upi+ ˜upi,N+˜n.The equations of mean flow can be derived by averaging Eq.(1)in the streamwise and spanwise directions.Here,＜·＞represents the averaging operator.

As we know,the Reynolds shear stress-＜＞can be modeled by eddy viscosity,-＜＞=νtdU/dy (νtis the eddy viscosity coefficient),and νtis given by the Cess model[23],

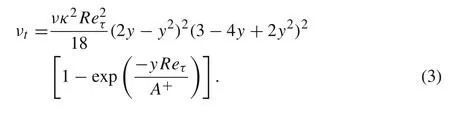
However, noting that the particle fluctuation velocityis not divergence-free, other second-order correlationsappear,in addition to the Reynolds shear stress- ＜˜u ˜v ＞. Thus the mean field cannot be solved directly.These other second-order correlations should be modeled by proper models.

2.2 Linearized perturbation equations

In this subsection, linearized perturbation equations for particle-laden turbulent flow are given. In the following,uppercase and lowercase letters represent the mean physical quantities and the fluctuations,respectively,for convenience.The physical quantities in Eq.(1)can then be decomposed as Ui+ui,Upi+upi,N+n,P+p.The linearized perturbation equations are expressed as follows:

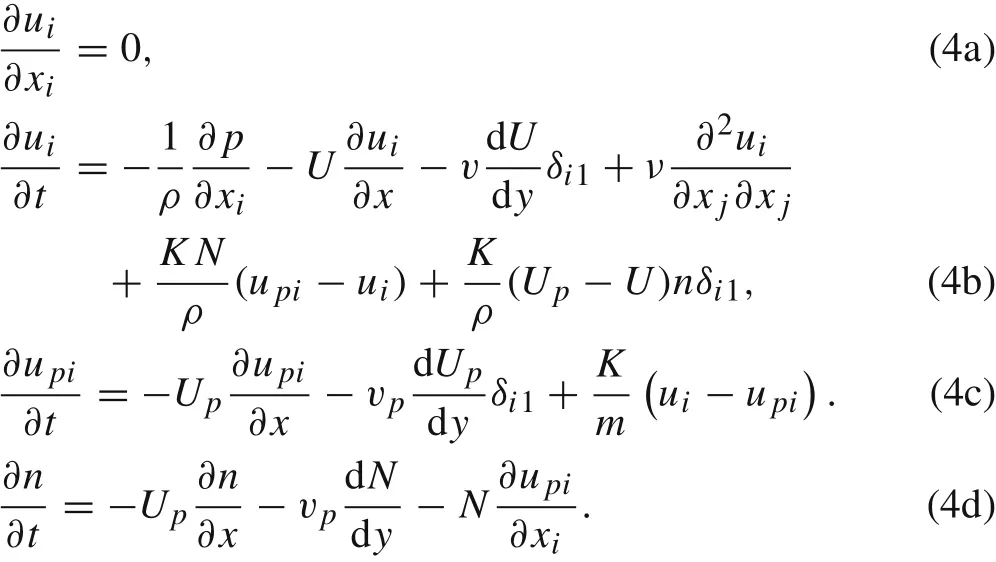
In this linearized system, the mean number density of particles is free from the equations of the mean flow, Eq. (2).However, it has been found that the particle number density distribution has a significant influence on the non-modal growth process in particle-laden channel flow [24]. Hence,we need to formulate a proper mean profile for the number density in turbulent particle-laden channel flow.For this problem,a previous study[21]found that the particles concentrate in the near-wall region when the Stokes number of particles is within a certain range. On the other hand,Boronin and Osiptsov [9] proposed a Gaussian distribution of the number density in their analysis for the transition of particle-laden flow.In this paper,we employ an approximate distribution for the mean number density N of particles.This distribution is based on a Gaussian function.

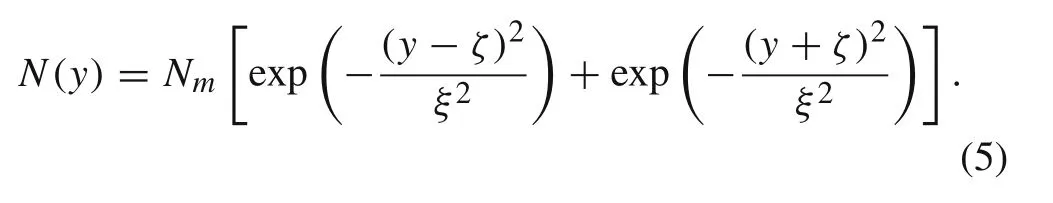
Here, ζ represents the location of the center of the particle layer,and ξ is the typical thickness of the particle layer. Nmis a normalized parameter.

When solving linearized perturbation equations,two projection operators are employed for the momentum equations of fluids in order to reduce the dimension of the linear system.The projection operators are defined as follows:

With these operators, the linearized fluid perturbation equations can be projected into the subspace spanned by the wall-normal fluid velocity v and the wall-normal fluid vorticity η.Then,Eq.(4)can be simplified as

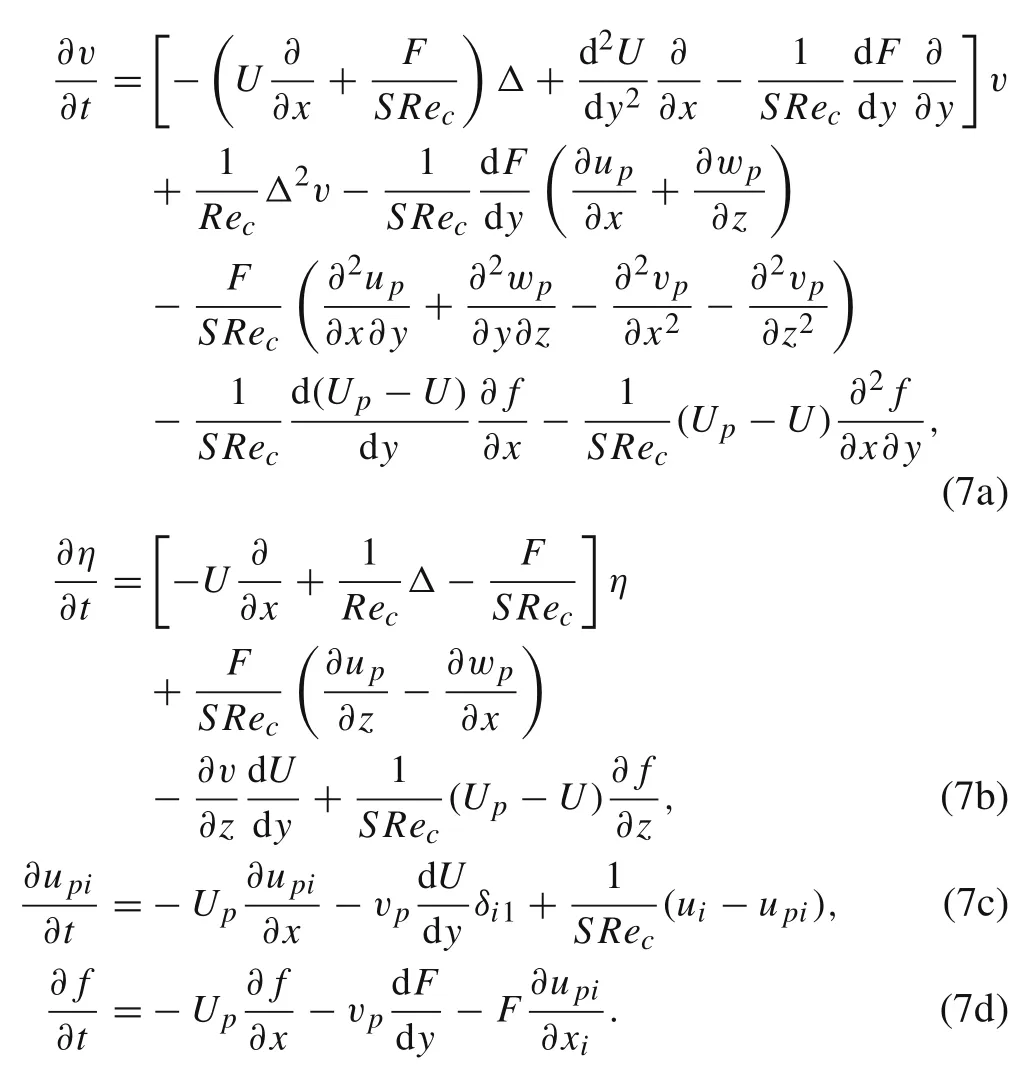
Here, for convenience, the non-dimensional velocities and vorticities are denoted by the same symbols,i.e.,v = v/Ucetc. The characteristic physical parameters are the centerline velocity Ucand the half-width of channel h; then the Reynolds number is defined as Rec= Uch/ν.is the Laplace operator. The non-dimensional mean number density and density fluctuation are defined as F = mN/ρ and f = mn/ρ, respectively. S is the Stokes number (S =τp/τ f =mν/Kh2).

A T-S wave solution of Eq.(7)is considered here,i.e.,any physical quantity q(t)in the linear system can be written as

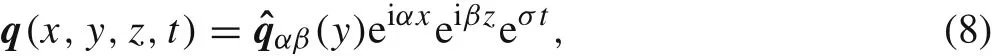
where α and β are the streamwise and spanwise wave numbers, respectively, and σ is the complex frequency of the equations.With this form of solutions,ordinary differential equations of the perturbation modes (denoted by ˆqαβ) can be derived directly from Eq. (7). The boundary conditions for the fluid flow at walls are the no-slip and non-penetrable conditions,i.e.,

and for the number density of particles,a compatible boundary condition is employed.

The computation of Eq.(7)is performed using a Chebyshev collocation method. With this method, the ordinary differential equations of perturbation modes degenerate into algebraic equations. Afterwards, a generalized eigenvalue problem is well defined:

where A and B represent the system matrices,and σ and x are the eigenvalue and eigenvector, respectively. From Eq.(10), the linear optimal growth in particle-laden turbulent flow is investigated below.

It is known that the turbulent mean flow is always linearly stable for all perturbations. However, the solutions of the linearized perturbation equations can undergo a transient growth process, due to the non-orthogonality of the eigenvectors. Any solution q(t) can be expressed by the linear combination of the eigenvectors:

Here,γmare the undetermined coefficients.With this expansion,the energy of this solution is defined as

The fluid velocity vector u is then expressed by the variables solved in Eq.(7).In addition,the energy function can be computed by

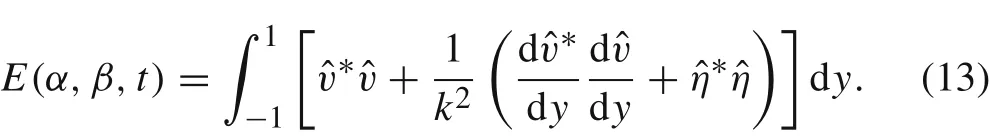
The symbol*stands for the complex conjugate of quantities,and the wave number k satisfies k2= α2+β2.As we can see, this expression is a quadratic form, and it can also be rewritten as

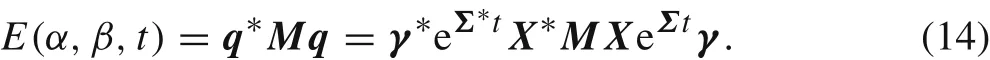
Here, the energy matrix M is Hermitian; Σ and γ are the frequency matrix and coefficient vector,respectively.Therefore,the energy of the perturbation at initial time is denoted by E(α,β,0) = γ*X*MXγ. Defining R = X*MX,Q = ReΣtR-1and ζ = Rγ, the energy amplification of the perturbation solution q(t)at time t is defined as

In particle-laden flow, the definition of energy amplification G can vary with different definitions of perturbation

energy functions.These different perturbation energy functions include the kinetic energy of fluids Ef=u*u, the kinetic energy of particles E p =and the square of the particle number densityHence, the energy amplifications can be defined as follows: fluid to fluid Gf-f(t)= Ef(t)/Ef(0),fluid to particle Gf-p(t)=Ep(t)/Ef(0), fluid to particle number density Gf-n=En(t)/Ef(0),fluid to all G f-a = (Ef(t)+ Ep(t))/Ef(0)and all to all Ga-a= (Ef(t)+ Ep(t))/(Ef(0)+ Ep(0)).Under these definitions, the different maximum energy amplifications Gmaxare well defined(for example,

The optimal energy amplification Goptis then defined as the maximum value ofin the wave number space:

3 Results

3.1 Model validation

In this subsection, the laminar case at Reynolds number Rec=2000 is investigated to validate the theoretical model and computational method proposed in Sect.2.

When considering the laminar case,the second-order correlations in Eq. (2) are zero, and the averaged momentum equations can be simplified as

From Eq.(18),the mean particle velocity Upis consistent with the mean fluid velocity U,and the mean particle number density N is free from the equations.That is,the mean fluid flow is a plane Poiseuille flow,and the distribution of particle velocity is the same as the distribution of fluid velocity(i.e.,Up=U),and N can be given arbitrarily for laminar cases.In this subsection, the non-dimensional mean number density of particles F is assumed as a constant in the field without special instructions. Figure 1 shows the time history of the energy amplifications Gf-fwith different non-dimensional mean number density F (F = 0.15 and 0.3).It is seen that the energy amplifications calculated by our model are in good agreement with the results in the previous study by Klinkenberg et al.[8].

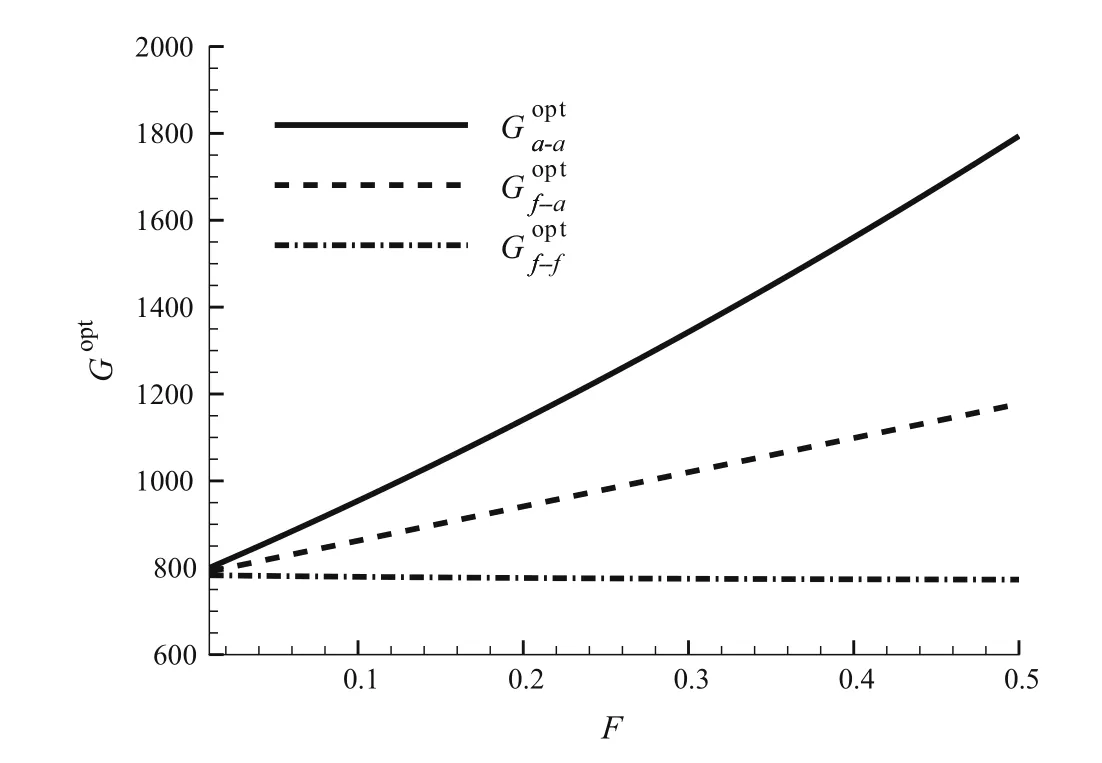
Fig. 2 Optimal energy amplifications Gopt with different definitionsare shown as the functions of the mean nondimensional density of particles F

The optimal energy amplifications Goptwith different definitions are also shown as a function of the non-dimensional mean number density F in Fig.2.It is seen that the energy amplificationsincrease linearly as the nondimensional mean number density F increases,whileis nearly unchanged with F. This result indicates that the energy transfer from fluid to particles for the large-scale perturbations in laminar particle-laden flow becomes more significant as the number density of particles increases.

Next,the optimal energy amplifications Goptvarying with the Stokes number S are given in Fig. 3. As the Stokes number S increases, only the energy amplification

increases significantly, while other energy amplificationsvary slowly.These results are consistent with the previous study[8].When the Stokes number S is large enough[i.e.,SRec→∞in Eq.(7)],the motion of fluids and particles is nearly decoupled.As a result,the particle velocity increases significantly because of the absence of dissipation in particle equations.

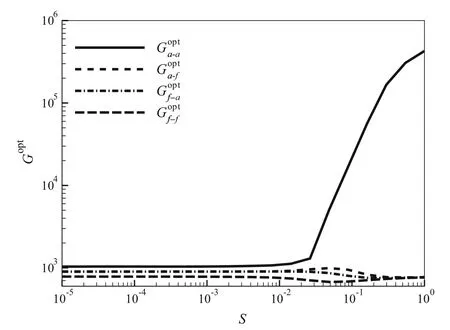
Fig. 3 Optimal energy amplifications Gopt with different definitions)are shown as a function of the Stokes number S

In the above analysis, the results by our computational model are quite consistent with the previous study by Klinkenberg et al. [8], which proves that the model can be employed to compute the linear optimal growth in particleladen channel flows. In contrast to previous studies, in our

Eulerian-Eulerian computational model,the mass equation of the density of particles is added. Hence, the optimal structures of particle concentration can be considered in our theoretical model. In the following, the optimal fluid and particle structures for the specific perturbation(αh =0.001 and βh = 2 i.e., almost streamwise independent disturbances) are investigated. In Fig. 4, the optimal streamwise flow velocity and the distribution of particle concentration under different definitions of the energy amplifications are shown together. It is found that the distribution of particles seems to be streaks which are similar with the optimal structures of fluid flows.The center of particle streaks in the wall-normal direction is almost the same as the fluid velocity streaks. However, the particle streaks and fluid streaks have a π/2 phase difference in the spanwise direction.Such a conclusion is consistent with the previous study by Boronin and Osiptsov[24]which is based on an equilibrium Eulerian method.

3.2 Turbulent case at Reτ =180

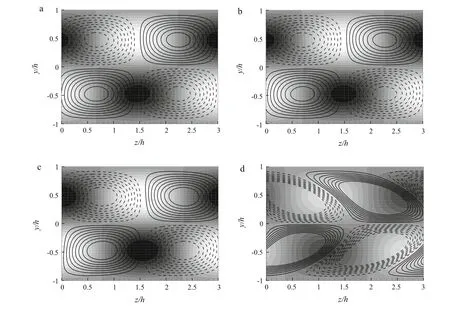
Fig.4 Optimal structures of the specific perturbation(αh =0.001 and βh =2)with different definitions of energy amplifications for S =5×10-5,F =0.15.a.The contour flood represents the streamwise fluctuation velocity u;the contour lines represent the non-dimensional number density fluctuation of the particles f;solid line f ＞0,dashed line f ＜0

In this subsection, we formulate the linear optimal growth analysis of the turbulent particle-laden channel flow.In turbulent cases,the proper mean flow solution(including the mean velocity and particle number density distribution)should be given first.In Sect.2.1,the motion of turbulent mean flow is described by Eq.(2).These equations need a proper closure model to compute the additional second-order correlations,which is not easy to deal with. However, when the Stokes number is small enough, the velocity difference between fluid and particle can be neglected,and the averaged momentum equation is simplified as

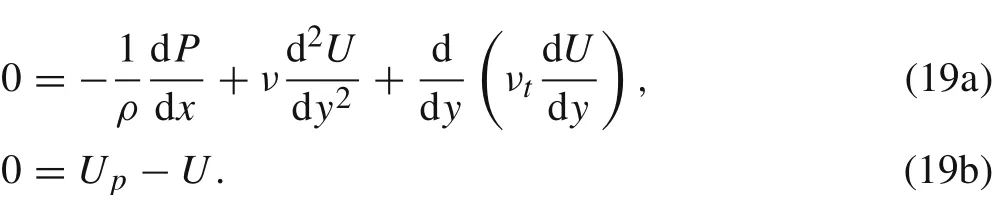
As we have seen, the mean velocities (U and Up) can be solved directly from Eq. (19) with the Cess model [see Eq. (3)], and the shape parameter A+is modified by the DNS results without particles [25,26]. The number density of particles is modeled by a Gaussian function proposed in Eq.(5),whose adjustable parameters are modified based on previous numerical simulations[3,21,27].

The physics problem considered here is the turbulent particle-laden flow at Reτ= 180, and the Stokes number of particles is set to be St+= SRe2τ/Rec= 1 in wall units. In this parameter scope, the Eulerian-Eulerian approach proposed in Sect. 2 is suitable [2]. Therefore, the optimal transient growth analysis is well defined.

First, we consider the turbulent case in which the maximum peak point of the mean number density distribution of particles is located at walls Fig.5b.To obtain the smallscale optimal structures(both fluid and particle structures),the transient growth time is limited to the turnover time in the buffer layer(i.e.,T+≈80)suggested by Butler and Farrell[10]. The definition of energy amplification employed here is Ga-abased on the total kinetic energy.

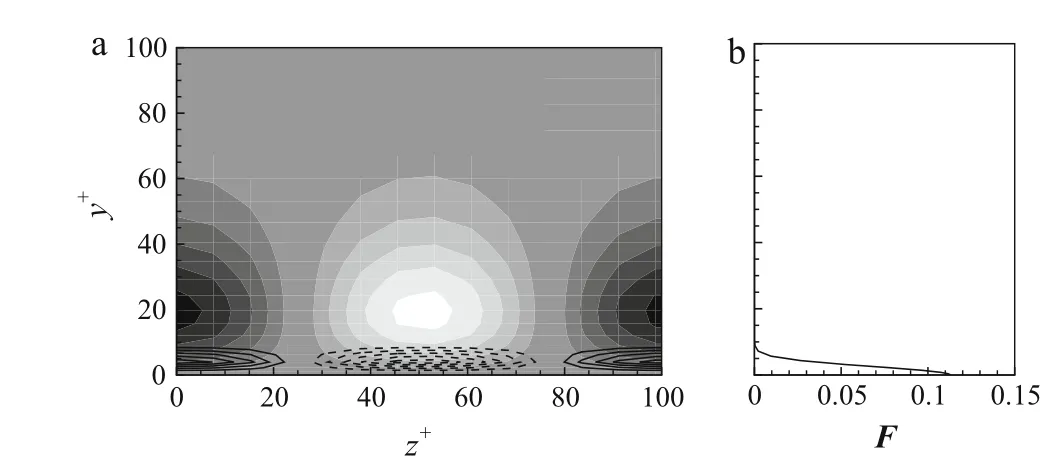
Fig.5 Optimal small-scale structures(a)with mean density profile(b).The contour flood represents the streamwise velocity,and the contour lines represent the number density fluctuation of particles; solid line f ＞0 and dashed line f ＜0

Figure 5 shows the optimal small-scale fluid and particle structures at Stokes number St+= 1. It is found that the optimal small-scale fluid structures are the streamwise streaks with typical spacing of 100 δνin wall units,which is the same as that without particles[25,26].The center of the fluid streaks is located at y+≈20 in the buffer layer. On the other hand, the optimal small-scale particle structures are also streamwise streaks,and their average spacing is also about 100 δν. However, the wall-normal center location of the particle streak is just below the center of the low-speed streak of the fluid.Moreover,the center of the particle streaks in the wall-normal direction is located at y+≈3,which is in the viscous sublayer,in contrast to the fluid streak.Such a phenomenon indicates that the particles will concentrate in the regions of low-speed streaks and form particle streaks due to optimal transient growth.

In the analysis above,we assumed that the maximum peak point of mean density is located at walls,which has not been confirmed in previous numerical research. In the study by Marchioli et al.[27],several groups computed particle-laden turbulent flow at Reτ=150 by the Lagrangian point-particle method, and they found that the maximum value of mean particle number density Nmaxis not always located at the walls. However, all the results from these groups showed that the maximum number density location is in the viscous sublayer(y+＜5).In present study,we consider the influence of the maximum number density location on the optimal small-scale structures in Fig.6.The maximum number density locations are set at ζ+= 0,5 and 10. As the location moves up, the optimal fluid streaks are nearly unchanged,while the optimal particle streaks are substantially changed:another pair of particle streaks appears below the original pair.In addition,the“positive”streaks and“negative”streaks appear on top of each other.

In Fig.7,the one-dimensional distribution of the streamwise velocity and particle number density is given. The location parameter ζ+is from 0 to 10.As ζ+increases,the location of the particle streaks moves away from walls.It is also found that the opposite streaks cannot appear if ζ+＜5.Furthermore, the maximum energy amplification Gmaxis shown as a function of the maximum non-dimensional mean number density value Fmfor the small-scale perturbation(i.e.,αh =0 and βh =11)in Fig.8.Here,the Stokes number is St+=1.It is seen that as Fmincreases,the energy amplificationsincrease, whileremains constant.This indicates that the energy transfer from fluid to particle becomes more significant as the number density of particles increases.

3.3 Turbulent case at Reτ =1000

In this subsection, the linear optimal growth in turbulent particle-laden flows at Reτ= 1000 is investigated. The Stokes number here is set at St+=1.

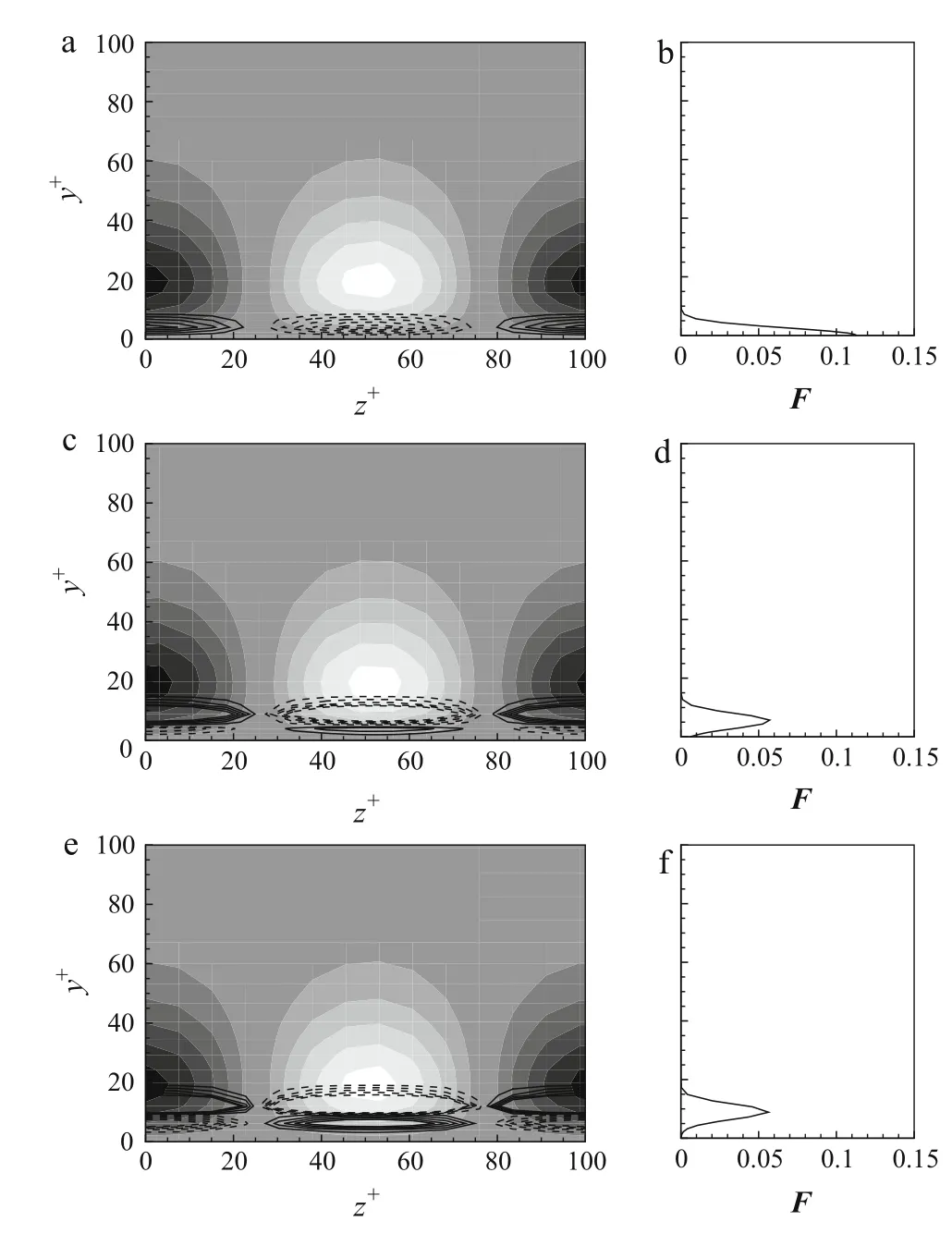
Fig.6 Small-scale optimal structures(a,c,e)and corresponding mean density distributions(b,d,f).The maximum density is located at(a,b)ζ+ =0,(c,d)ζ+ =5,(e,f)ζ+ =10

In Sect. 3.2, the mean fluid velocity U(y), mean particle velocity Up(y)and mean particle number density F(y)are obtained from the model equations with some assumptions.Here,to be more accurate and to test these assumptions,these mean quantities are obtained directly from the DNS data for the particle-laden turbulent flow at Reτ= 1000 by the equilibrium Eulerian approach[28].In Fig.9,the mean distribution of streamwise velocity and particle number density and the Reynolds stress are shown.We can see that the difference between the mean fluid velocity and the particle velocity in DNS can be negligible (about 2%-3%). Therefore,the assumption Up=U is reasonable for particle-laden flows with such Stokes numbers.It is also shown that the peak value of the particle number density distribution is located at around y+=1.

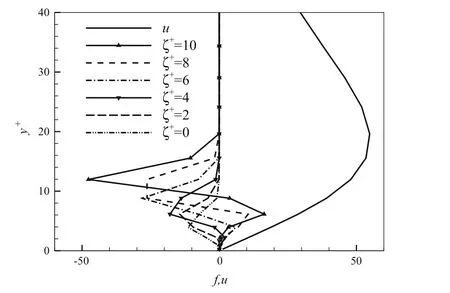
Fig.7 Distributions of the streamwise velocity fluctuations and particle density fluctuations vary with y+.The location parameter ζ+is from 0 to 10

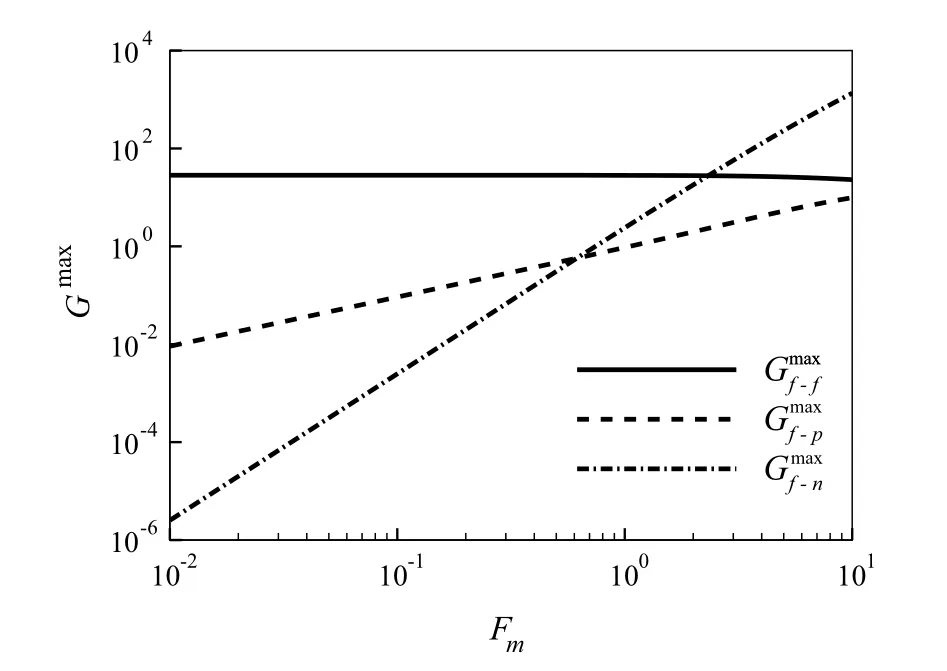
Fig.8 Distribution of the maximum energy amplification Gmax varies with the maximum density value Fm

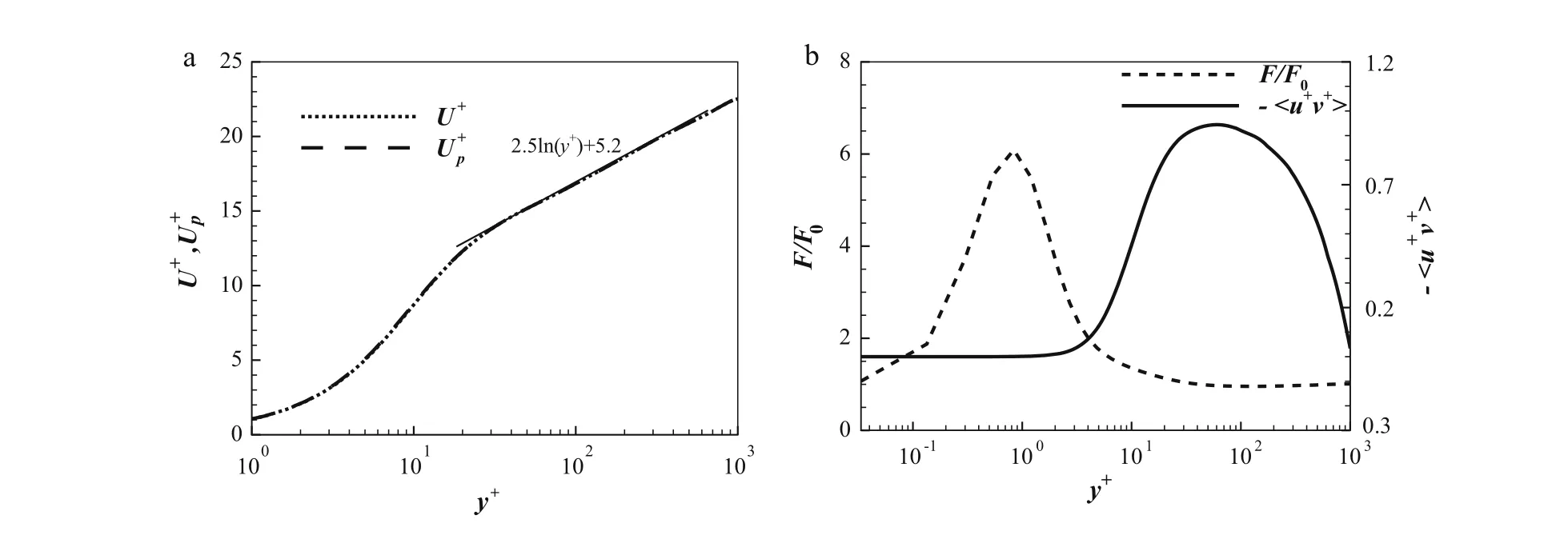
Fig.9 Mean quantities from DNS.a Mean fluid velocity and particle velocity,b mean density of particles and Reynolds stress. F0 is the averaged non-dimensional particle number density of the whole channel,and the velocities are normalized by the friction velocity uτ

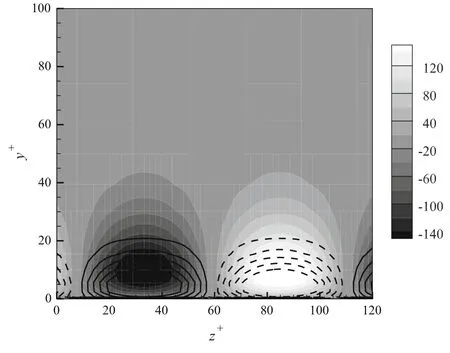
Fig.10 Optimal small-scale structures for the turbulent case at Reτ =1000

In the following,small-scale and large-scale perturbations are investigated,respectively.For small-scale perturbations,the transient growth time is set as the eddy turnover time in the buffer layer,as was mentioned in Sect.3.2,i.e.,T+≈80.When considering the large-scale perturbations, no limit is set for the transient growth time, and an iterative process during a time interval is adopted for the computation of the transient growth.

The optimal small-scale fluid structure and particle structure are displayed together in Fig. 10. It is seen that the relative location between the fluid streaks and particle streaks is almost the same as that in Fig.5 at low Reynolds numbers.That is to say,the Reynolds number effect seems to be nonsignificant for the near-wall small-scale structures(including fluid and particle structures).

Next, we consider the large-scale optimal structures,which are given in Fig. 11. In order to properly draw both small-scale and large-scale structures,the logarithmic coordinate is employed in the wall-normal direction. Here,represents the distance from walls measured by the half width of the channel h. It is seen that the optimal fluid structures are almost the same as in the turbulent channel flow without particles [29], and the optimal particle structures are concentrated in the buffer layer.This indicates that the optimal large-scale particle structures remain in the nearwall region and do not enter the outer region as was seen with the large-scale fluid structures.The center of the particle structures is located at y+≈10,close to the location of the optimal small-scale particle structures. This is because the number density of the particles in the near-wall region is significantly larger than in other regions in the distribution of mean flow,and the number density is almost unchanged in the outer region.As a result,the gradient of mean particle number density is nearly 0,and the production of its fluctuation is very small.Thus,there is no large-scale particle structure in the outer region in the absence of this production.

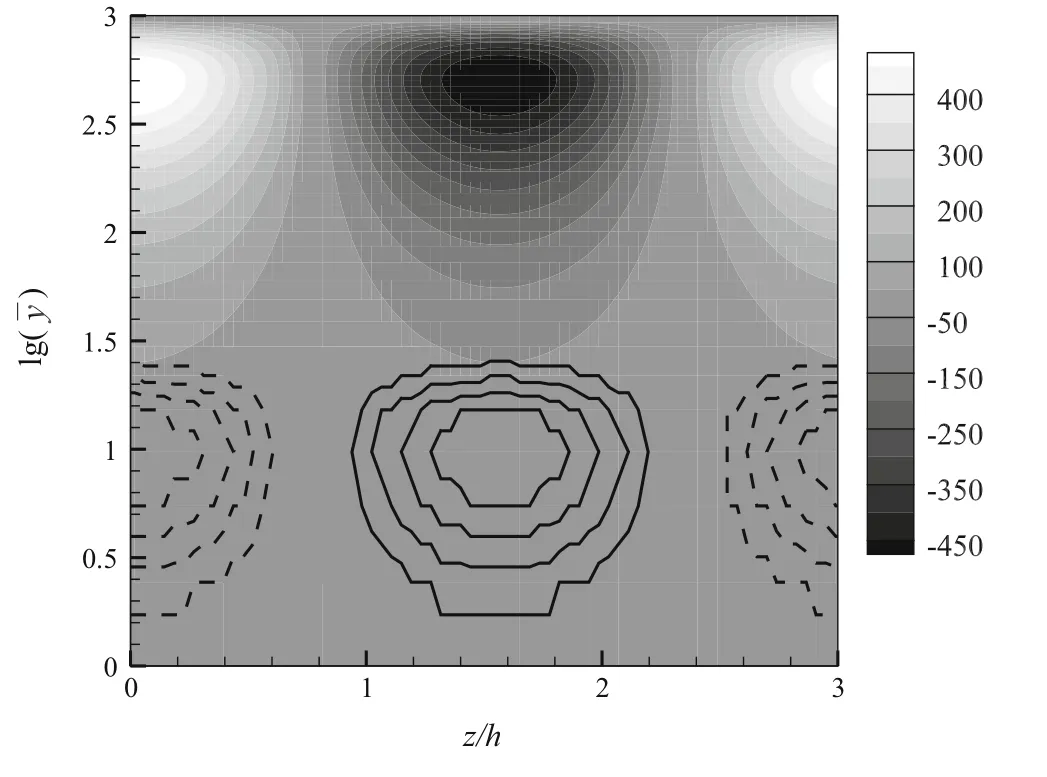
Fig.11 Optimal large-scale structures for the turbulent case at Reτ =1000

4 Conclusions

In this paper, optimal transient growth in particle-laden turbulent channel flow is investigated.The computational model is based on the Eulerian-Eulerian approach. The model is first validated in laminar cases.The computational model is then adopted to analyze the turbulent particle-laden channel flow at two typical Reynolds numbers,i.e., Reτ= 180 and Reτ= 1000.It is found that the linear optimal growth can explain the formation of the particle streaks,and the typical spacing of these streaks is about 100 δν,which is the same as the spacing of the fluid streaks.On the other hand,the high particle density fluctuation region is just below the low-speed fluid streaks.Such a phenomenon has been found in previous direct numerical simulations.These results prove that linear optimal transient growth is likely a dominant mechanism for the formation of small-scale particle structures.

For the high Reynolds number case at Reτ= 1000, it is found that the optimal large-scale particle structures are concentrated in the near-wall region,which is quite different from the large-scale fluid structures.Such a result is due to the distribution of the number density of particles in mean flow.The gradient of the particle density in the outer region is nearly 0,so the production of number density fluctuation is too small to form large-scale structures in the outer region.

AcknowledgementsWe would like to express our sincere gratitude to Professor Luca Brandt, who gave us great help by providing us with necessary materials and valuable advice.

Appendix

In the appendix, the exact forms of the system matrices in Eq. (10) are given. First, the variable x is expressed byThe system matrices can then be fully described with Eq.(7),

Here,Here, the matrix D = d/dy is the differential operator, and the matrices Lxxrepresent the linear operators that are defined below.

In Eq. (20), the operators Los, Lsqand Lcare the Orr-Sommerfeld, Squire and linear coupling operators, respectively.Their exact expressions can be given by

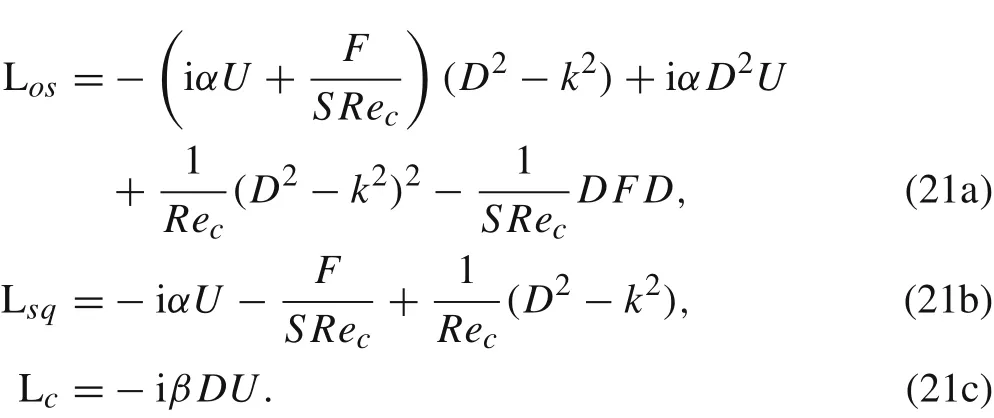
These three operators were also involved in previous studies [20,25], but the other linear operators are only required when considering particle-laden flows. The expressions of these operators are summarized as follows:

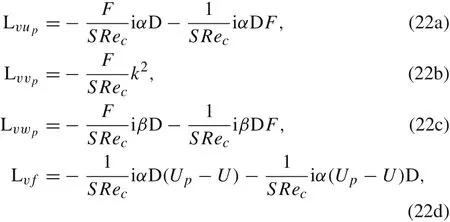
With these expressions,the system matrices A and B in Eq.(10)are well defined.