Geometric and material nonlinearities of sandwich beams under static loads

Guangtao Wei·Yang Jin·Linzhi Wu,2

Abstract A new theory developed from extended high-order sandwich panel theory(EHSAPT)is set up to assess the static response of sandwich panels by considering the geometrical and material nonlinearities simultaneously.The geometrical nonlinearity is considered by adopting the Green-Lagrange-type strain for the face sheets and core.The material nonlinearity is included as a piecewise function matched to the experimental stress-strain curve using a polynomial fitting technique.A Ritz technique is applied to solve the governing equations.The results show that the stress stiffening feature is well captured in the geometric nonlinear analysis.The effect of the geometric nonlinearity in the face sheets on the displacement response is more significant when the stiffness ratio of the face sheets to the core is large. The geometric nonlinearity decreases the shear stress and increases the normal stress in the sandwich core. By comparison with open literature and finite element simulations, the present nonlinear EHSAPT is shown to be sufficiently precise for estimating the nonlinear static response of sandwich beams by considering the geometric and material nonlinearities simultaneously.

Keywords Extended high-order sandwich panel theory·Geometrical nonlinearity·Material nonlinearity·Ritz method

1 Introduction

Sandwich beams consisting of two thin panels and a thick core are widely used in industry due to their outstanding strength and stiffness and good energy absorption.In particular,the panels applied in ships are usually made of a metal material such as 304 stainless steel,and a core material that may be metal,polymer foam,balsa wood,or the like.Mostly,it is acceptable to assume linear and elastic deformation of sandwich beams under small loads. In practice,however,geometrical and material nonlinearities generally occur in the sandwich core and face sheets when they are subjected to extreme loads. Thus, the effects of such geometric nonlinearity and plastic behavior of the constituent materials on the static response of sandwich beams should be considered.

Many theories have been presented to study the mechanical characteristics of sandwich beams. The early classical theory,named the first-order shear theory(FOST),only considering the shear resistance of the core but with no axial rigidity or any transverse compression, has been proven to be suitable for highly stiff cores, but not for soft ones in mechanical analyses of sandwich beams.Later,in 1992,by including the shear effects and transverse compressibility in the sandwich core, Frostig et al. [1] proposed a high-order sandwich panel theory(HSAPT)which is accurate for sandwich beams with highly flexible cores.However,due to the complexity of the governing equations,the axial rigidity in the sandwich core is still ignored. To eliminate the errors generated from such simplifications,Phan et al.[2]proposed a new theory called extended high-order sandwich panel theory(EHSAPT),which includes the axial rigidity in the core.This theory is extremely accurate and can be used to predict the displacement and stress in static or dynamic analyses of sandwich beams by comparison with elastic solutions, no matter whether the cores are extremely soft or hard[3-8].

The majority of sandwich beam theories have been developed for linear elastic response at small strains [9-11].However, sandwich beams used in practice usually absorb energy from external loads.One of the most relevant issues is thus how to estimate the influence of geometrical nonlinearity on the static response of sandwich beams[12].Indeed,geometric equations, such as the Green-Lagrange- or von Karman-type strains for the core or face sheets,can describe the geometric nonlinearity but make the governing equations complex and nearly impossible to solve. Therefore, some assumptions and simplifications are made by ignoring the nonlinear terms, and numerical techniques are adopted to solve the nonlinear governing equations.A nonlinear HSAPT model presented by Sokolinsky et al.[13,14]revealed that the changes in the geometric topology, mechanical characteristics, and boundaries may cause qualitative changes in the mechanical response of sandwich panels. A four-point bending test was conducted to demonstrate the significant geometrical nonlinearity near the internal supports. Then,many investigations were carried out based on the nonlinear HSAPT to reveal the geometric nonlinear behavior of sandwich beams. In their work, Hohe et al. [15] employed von Karman-type strains to establish a doubly curved shell theory for sandwich panels with transversely compressible cores by considering the geometric nonlinearity.Two simplified models were proposed by Frostig et al.[16]to investigate the geometric nonlinearity by employing nonlinear relations for each sandwich layer for large displacements and moderate rotation.In 2014,a nonlinear EHSAPT was presented,adopting von Karman strains for the face sheets and sandwich core[17,18].In 2016,Moita et al.[19]extended a finite element model to investigate the static nonlinear response of sandwich structures such as curved shells and plates.More recently,all the nonlinear terms were assessed by Yuan et al.[4, 6, 20-22] based on EHSAPT. This nonlinear EHSAPT model has been proven to be effective for both static and dynamic analyses.

Another associated problem is the difficulty in estimating the nonlinear behavior of the materials in the sandwich layers. Most materials used in sandwich beams, including metals, foams, etc., cannot be assumed to be elastic under intense loads owing to the occurrence of plastic deformation. However, literature survey reveals that very little research on sandwich beam/plate theories consider the plastic response of materials. By ignoring the global axial and flexural deflection, Xie et al. [23] introduced a theoretical model to determine the plastic indentation characteristics of a foam core in sandwich beams.An improved extended highorder model was proposed by Salami et al. [18], where the foam cores with bilinear elastoplastic constitutive relations are considered. An iterative technique is utilized to obtain accurate solutions, revealing that the bilinear elastoplastic behavior in materials is significant for the static response of sandwich beams,including displacements,stresses,strains,etc., and should be considered for more accurate calculation.A similar model based on HSAPT to detect the elastic and plastic regions using an iterative procedure was applied by Rezaeifard et al. [24]. Unlike the complicated solution processes mentioned above,a comprehensive method based on a Ritz method is presented herein to solve the governing equations.Besides,instead of a bilinear stress-strain relation for the sandwich beam,a more general relationship between stress and strain based on tensile/compression test data is applied to study the elastoplastic behavior of sandwich beams under static loads.

It can be concluded from the literature review above that elastoplastic materials,such as metals and polymers,usually suffer nonlinear deformation due to their relatively low stiffness and plastic characteristics under intense loading,while there is little open literature on EHSAPT that takes account of the geometrically nonlinear terms and arbitrary elastoplastic behavior of such materials.In the current analyses,a new model is applied to include the geometrical and material nonlinearities simultaneously according to EHSAPT,and the displacement and stress responses under static loadings are analyzed.An elastic-plastic stress-strain relationship for the core layer is obtained by polynomial fitting of experimental data,and Green-Lagrange strains are utilized for each sandwich layer.The Ritz-based technique is improved to derive a new and fast convergence method for the nonlinear governing equations. A set of MATLAB programs suitable for arbitrary boundary conditions is developed based on symbolic operations. Comparisons with previous literature are carried out to validate the present model.

2 Theory and derivations

A sandwich beam is plotted in Fig. 1. The span length and width are denoted as a and d.The core and face sheet thicknesses are denoted as 2h and f, respectively. The material parameters are the shear modulus G, Young’s modulus E,and Poisson ratio ν. At the left side of the beam, a two dimensional Cartesian coordinate system oxz is placed with origin o at the center.The superscripts“b,”“c,”and“t”denote the bottom face sheet,core,and top face sheet,respectively,while the subscripts“1”and 3 refer to the axial x and transverse z direction,respectively.The subscript“0”corresponds to the middle face of the corresponding sandwich layer.The subscripts (,z) and (,x) are the derivative operators d/dz and d/dx,respectively.Based on extended high-order sandwich panel theory(EHSAPT),the following assumptions are made in the analyses:

1. The linear elastic face sheets follow the Euler-Bernoulli assumptions,with no shear strain involved.

2. The two-dimensional core follows the isotropic hardening rule.The whole yield surface expands evenly in the plastic flow.

Fig.1 Coordinate system and geometry of sandwich beam configuration

3. The core and face sheets are perfectly combined with no occurrence of delamination.

4. The deformation of sandwich beams is small, thus the Cauchy stress can be used.

According to the original description of EHSAPT[2],the displacement fields of the core and top/bottom face sheets are given as

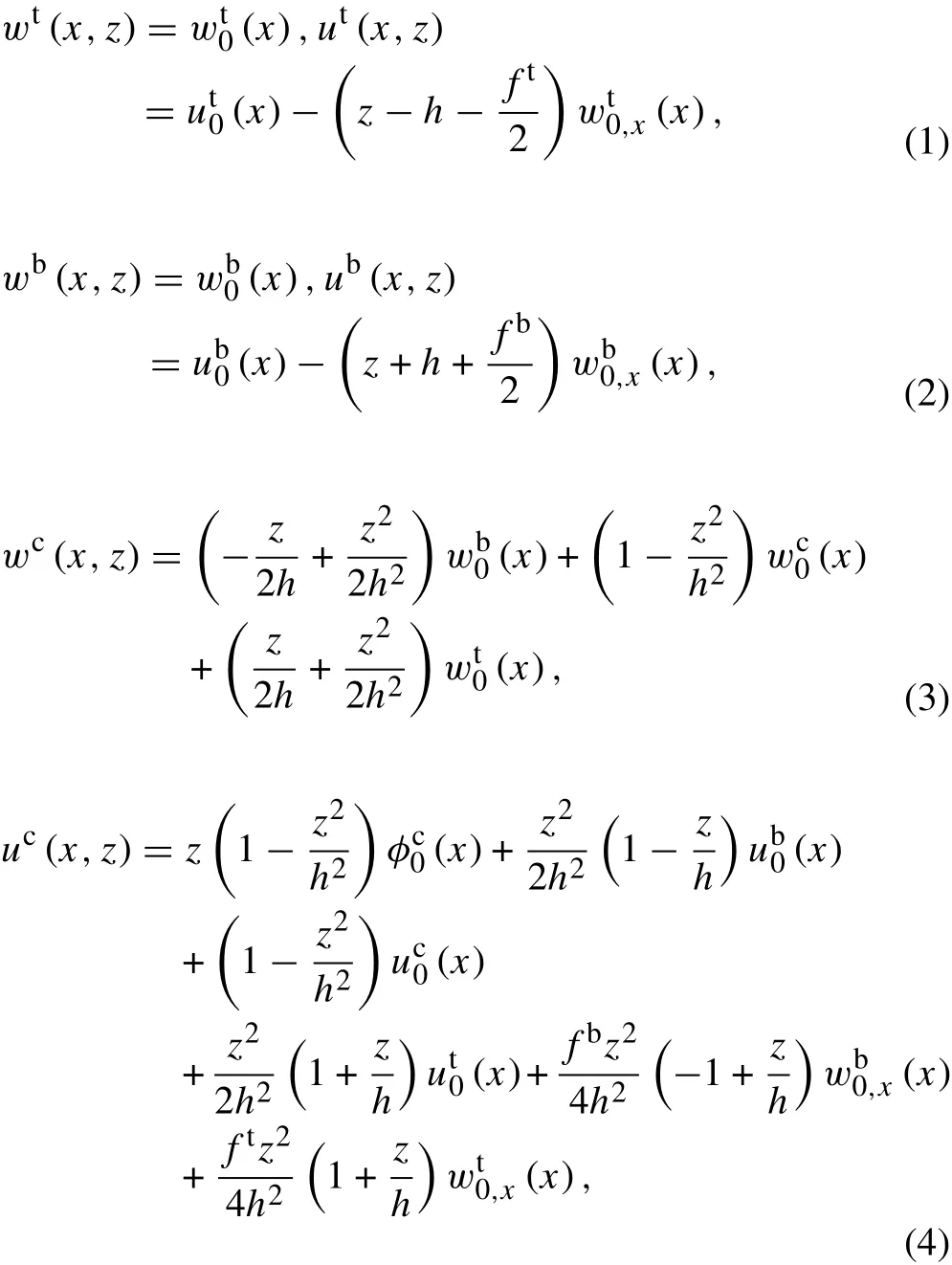
where w and u are the transverse and axial displacements,respectively,and φc0is the slope at the centroid.

The Green-Lagrange strains are adopted for the face sheets:

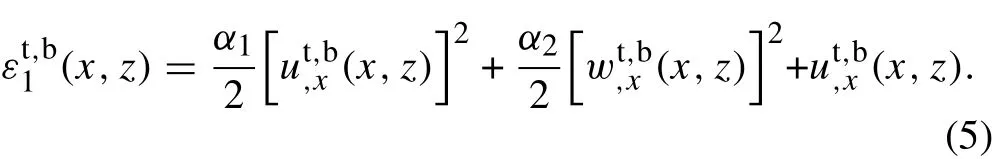
The nonlinear forms of the normal strains εc1and εc3and shear strain γc13in the core are

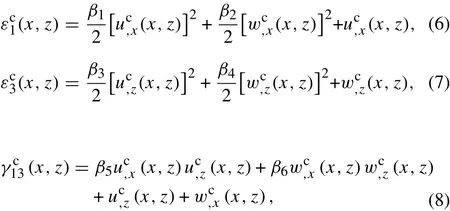
where the constant coefficients αi(i =1,2) and β j(j =1,2,...,6)are equal to either 0 or 1 according to the nonlinear terms concerned.When the core and face sheets are orthotropic and the face sheets follow the Euler-Bernoulli assumptions,the Cauchy stresses can be obtained from

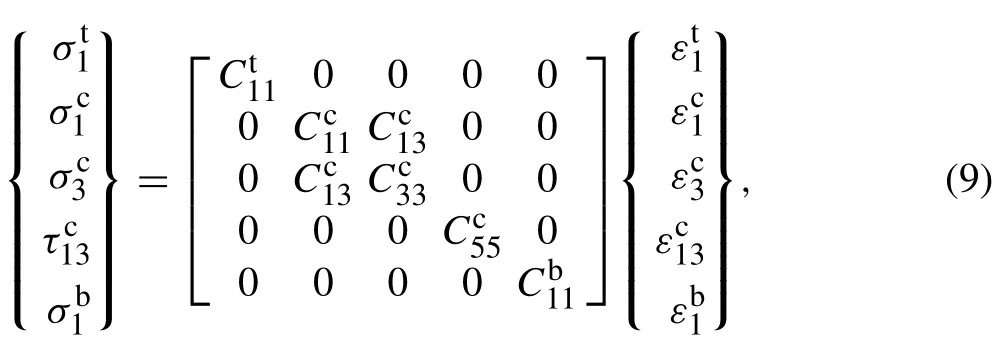
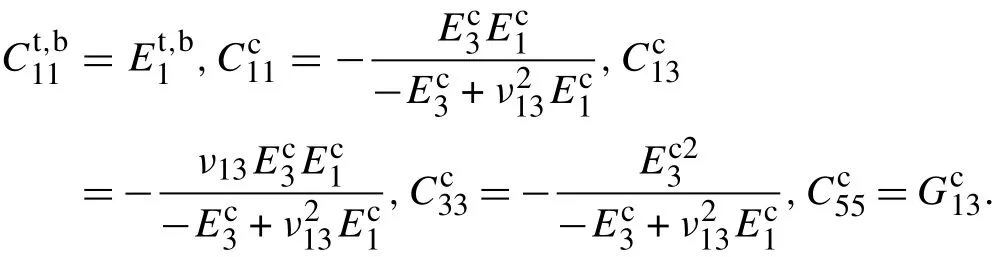
Once the plastic deformation of materials in the core is included,the stress-strain relations are no longer linear and theCcijinEq.(9)are no longer constants.In practice,stress-strain curves are generally captured from experimental data based on axial tensile or compressive tests. To obtain an expression for the stress-strain relationship, a polynomial interpolation method is adopted to fit the plastic section of the stress-strain curve,while the elastic modulus in the elastic section remains unchanged. The experimental stress-strain curve is then

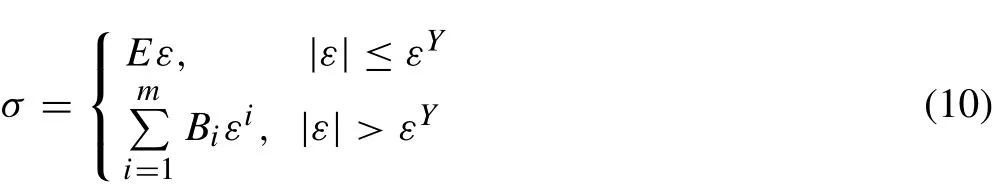
where the vector B denotes the fitting parameters,which can be easily determined by a MATLAB program.Increasing the order m,the fit curve approaches the experimental one.

3 Numerical formulation

When using various sandwich beam/plate theories,most of the analytical solutions are only acquired for simply supported boundaries.When considering more complex boundary conditions,no analytical solution is generally available.Recently,numerical solutions using the Ritz method based on EHSAPT or HSAPT have been investigated.The efficiency of the Ritz method largely relies on the trial functions,including polynomial series [24] or power series [18] functions.These theories appear to be relatively slow in convergence.A finite element model based on EHSAPT and developed by Yuan et al. [4] has been proven to be highly accurate.Inspired by the finite element form of EHSAPT,a Ritz-based model is implemented here by separating the sandwich beam into several elements and interpolating the displacement in each element using a polynomial interpolation technique.In addition,unlike the finite element method EHSAPT(FEMEHSAPT) used in Ref. [4], the Ritz-based method enables solutions to obtained directly by symbolic operations,which is easier to understand and program.

Firstly, the sandwich beam is separated into n elements along the x-axis, and each node is assigned nine variables,viz.

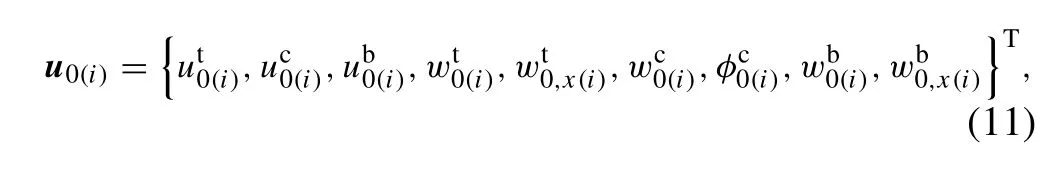
where the subscript i denotes the i-th node along the x-axis.

The node displacements, u0(i)and u0(i+1), are used to interpolate the displacement at the middle face of the i-th element,u0e(i).Since the displacements φc0and ut,c,b0should be C0-continuous, and wt,c,b0should be C1-continuous in Eqs. (1)-(4), in this paper the Lagrange polynomials are utilized to interpolate φc0and ut,c,b0. The transverse displacements wt,c,b0are interpolated by Hermite quadratic interpolation polynomials. Thus, the middle face displacements u0e(i)are

where A and B are described in detail in Appendix.Substituting Eq.(12)into Eqs.(1-4),the displacement vector ue(i)=in the element can be obtained.Then,the total potential energy in the i-th element is

where Wiis the potential energy from the applied loads and Uiis the strain energy in the i-th element,which are

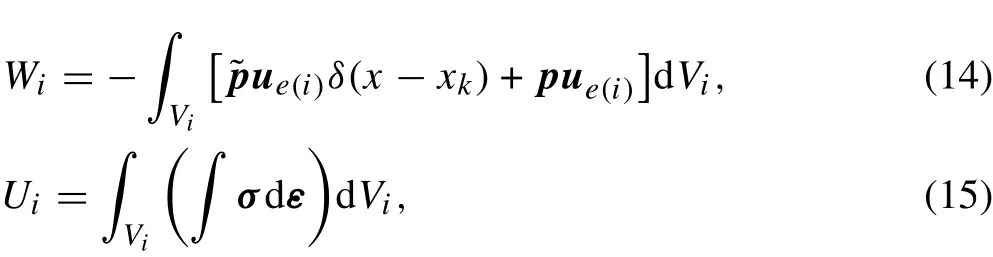
qt,c,band pt,c,bdenote the distributed forces along the z-axis and x-axis,respectively,and mt,c,bis the distributed moment in unit width.Alsoandare the corresponding concentrated forces and moments,respectively.xkis the x-axial location of applied loads,δ(x)is the Dirac delta function,and Viis the volume of the i-th element.Thus,from the principle of minimum potential energy,the governing equations can be derived as

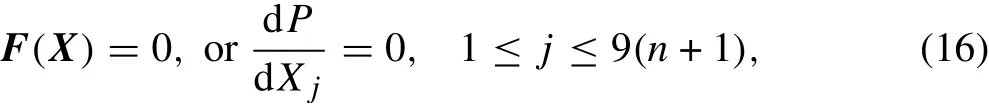
A modified Newton-Raphson technique is derived here to solve Eq.(16):

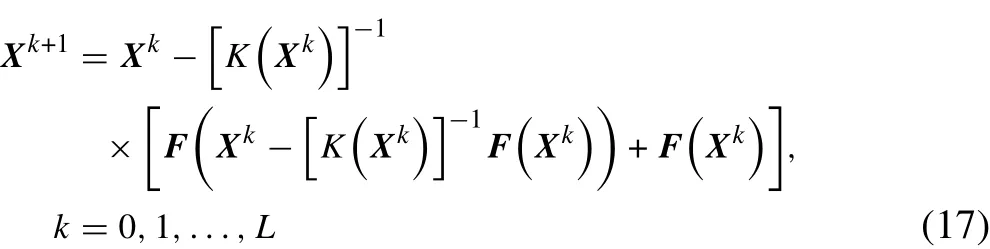
where Xkis the approximate solution in the k-th iteration.The matrix K in Eq.(17)is

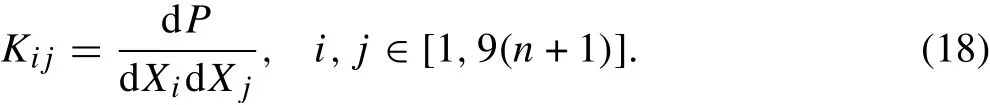
Table 1 Material characteristics of sandwich beam(moduli in GPa)

According to the previous analysis,the expressions for the stress-strain relation differ in the plastic and elastic regions,so a procedure to detect the elastic and plastic regions in the sandwich beam is necessary.Here,an iteration technique analogous to that applied in Ref.[17]is utilized to identify the elastic edges as follows:

1. The initial plastic regions where the stress is larger than the yield stress are detected after the fully elastic governing equations are solved.

2. The strain energy in the elastic and plastic regions is calculated, respectively, by adopting the corresponding expressions of the stress-strain relations,and the governing equations are re-solved to amend the edges of each region.

3. The second step is repeated until the changes of elastic edges along the x-axis is less than 1%of the span length a.

4 Results and discussion

4.1 Verification

To validate the numerical solutions of the present model,the linear responses of sandwich beams with no considerations of geometrical and material nonlinearities are compared with the analytical results in Ref. [2] for the simple supported boundary.Assigning the coefficients in Eqs.(5-8)the values of αi= β j = 0 (i = 1,2 and j = 1,2,...,6) and making the materials purely elastic, the present model reduces to linear EHSAPT. The geometrical parameters are: length a = 400 mm, face thickness ft= fb= 2 mm, and core thickness 2h =16 mm.The material parameters of the glass phenolic honeycomb core and graphite epoxy face sheets are presented in Table 1. A transversely applied load F sin(πx/a)is distributed on the top face sheet.The magnitude of the transverse displacement on the top face is normalized bySolid elements (CHEXA) and eightnode continuum shell(CQUAD4)elements are implemented for the core and the face sheets, respectively, for the three dimensional finite element simulation using the commercial software OptiStruct. The mesh size is 1 mm. The core and face sheets are fully bonded at the interfaces,with no occurrence of delamination.As seen in Fig.2,the numerical results of EHSAPT coincide well with the analytical ones and are close to finite element results.

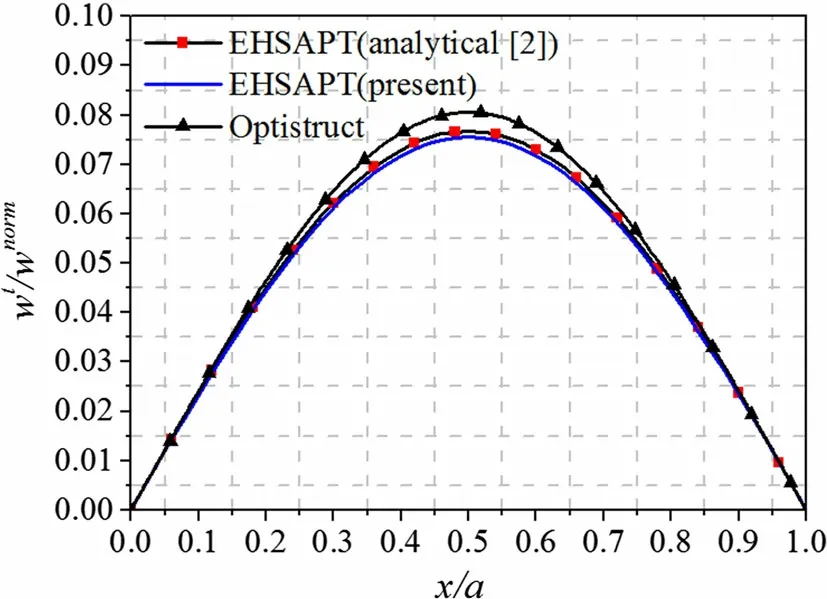
Fig.2 Comparisons of transverse displacement at top face sheet from EHSAPT and finite element simulation by OptiStruct

Since open literature lacks theoretical results on the nonlinear responses of sandwich beams considering arbitrary material plastic behavior, the responses from the proposed theory are acquired based on a bilinear assumption for the core. The geometry is: length a = 130 mm, width d = 30 mm, face thickness ft= fb= 2.7 mm, and core thickness 2h = 10 mm. The elastic modulus of the face is 48.9 GPa, and the material properties of the core are: elastic modulus 217 MPa,shear modulus 76 MPa,and yielding shear stress 2.6 MPa. Similar to Refs. [24-26], the plastic behavior of the core is indicated by a bilinear stress-strain relation, with the bilinear ratio θ. When θ = 1, the core is pure elastic. The fitting order m = 1 in Eq. (10) can fully describe the plastic behavior of core materials. A line load L =-2060 N is implemented at the middle of the top face,with the two ends of sandwich beams simply supported.

As seen in Fig. 3, when all the geometrical nonlinear terms are included, namely αi= βj= 1(i =1,2 and j =1,2,...,6), and the core materials are elastic (θ = 1) or elastoplastic (θ = 0.01), the present solutions are close to the theoretical results and the FE calculation accomplished by Abaqus code from Ref.[17].The slight difference can be understood based on the fact that the sandwich beam is considered as a whole element in Ref.[17]and the trial functions are in the form of power series,(x/a)j. Specifically, these trial functions with respect to x are not symmetrical about the center of the sandwich beam,and when the beams are exposed to symmetrical loads and boundaries,the order j should be sufficiently large to obtain the symmetrical mechanical response, which seems relatively time-consuming to converge. In the present model,the sandwich panel is divided into several elements, with Lagrange and Hermite polynomials as trial functions in each element.The present model allows faster convergence when solving the governing equation,requiring approximately 10 elements to converge in the current analysis(Fig.4).Additionally,all the geometric nonlinear terms are included here when assessing the effects of geometric nonlinearity,unlike the model in Ref.[17],where von Karman-type strains(only α2=β2=1)are adopted.

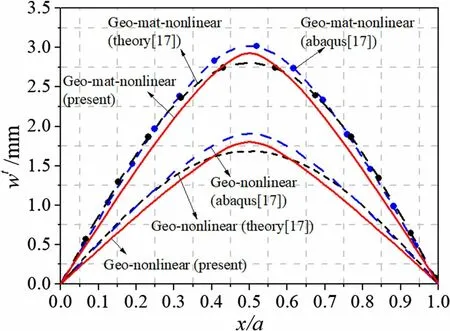
Fig.3 Comparisons of present geometrical nonlinear and geometric/material nonlinear model with open literature

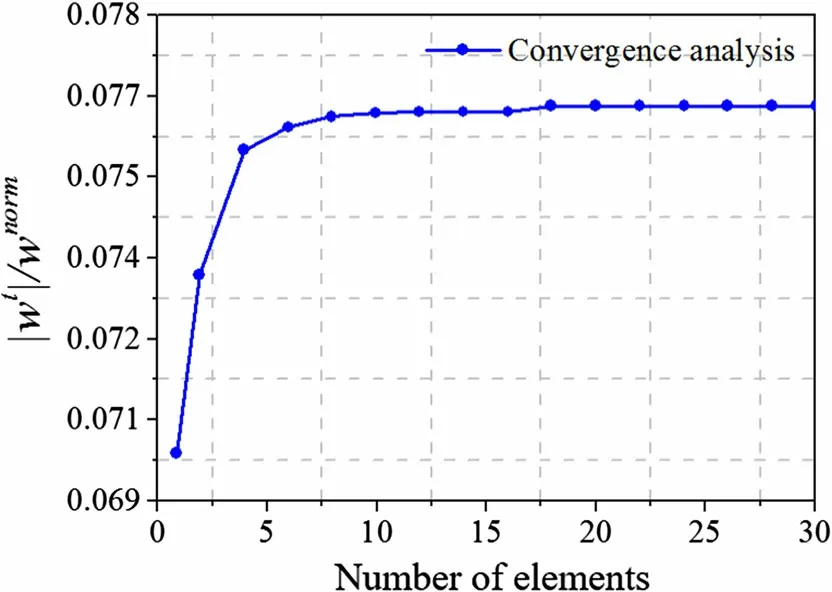
Fig.4 Convergence analysis of normalized transverse displacement of top face sheet at x =a/2 versus number of elements

4.2 Geometric nonlinearity

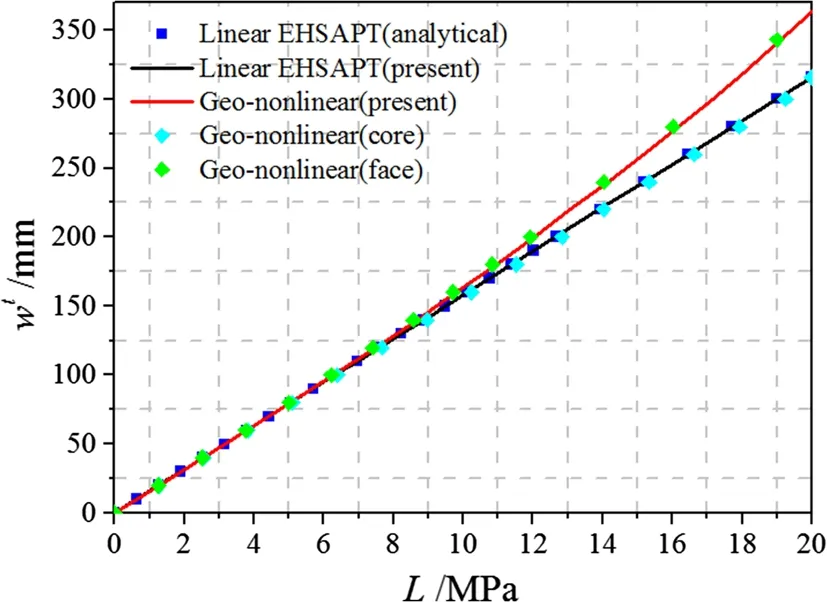
Fig.5 Static load versus transverse displacement at center of top face sheet from linear and geometric nonlinear EHSAPT

To estimate the influence of geometrical nonlinearity in different layers on the static mechanic response of sandwich beams, diverse combinations of nonlinear terms in Eqs.(5-8)are considered here by assigning the coefficients αi(i =1,2)and βj(j =1,2,...,6)to 1 or 0.The materials in each sandwich layer are all assumed to be entirely elastic. The geometry and materials, as well as the loads,are consistent with the example from Ref. [2]. The curves describing the load L with respect to the transverse displacement at the top face center are given in Fig.5.The analytical method from Ref.[2]is applied to verify the present numerical results of linear EHSAPT.As seen,the present solutions of the linear EHSAPT show good agreement with the analytical ones. The displacement increases linearly with the load. When all the geometric nonlinear terms are included,the fully geometric nonlinearity curve exhibits typical stress stiffening effects. It reveals that the displacement response will be over predicted if the in-plane membrane stiffening is not captured.

Comparison of geometric nonlinearity in the face (only α1=α2=1)and in the core(only β j =1, j =1,2,...,6)suggests that the core geometrical nonlinearity has a slight influence on the transverse displacement,while the face geometrical nonlinearity has a relatively greater influence on the transverse displacement.It is foreseeable that,due to the high ratio of elastic modulus Et,b/Ec,the strain energy of nonlinear components in the face sheets is much larger than that in the core,thus contributing more to the Jacobi matrix K in Eq.(18).

Once all the geometric nonlinear terms are considered and the sandwich beam is exposed to a distributed load L =0.6 sin(πx/a) on the top face,the transverse displacement of the midface in each layer along the half-panel is plotted in Fig.6.Both the linear and geometrically nonlinear responses of the present EHSAPT are validated by the finite element results. As seen, the present EHSAPT agrees well with the FEM,and when the geometric nonlinearity is considered,the magnitudes of the transverse displacement in the middle of each layer are smaller than those obtained using the linear response,with a maximum decrease of approximately 46%.It can thus be concluded that the effect of the geometric nonlinearity on the displacement response of sandwich beams is significant.

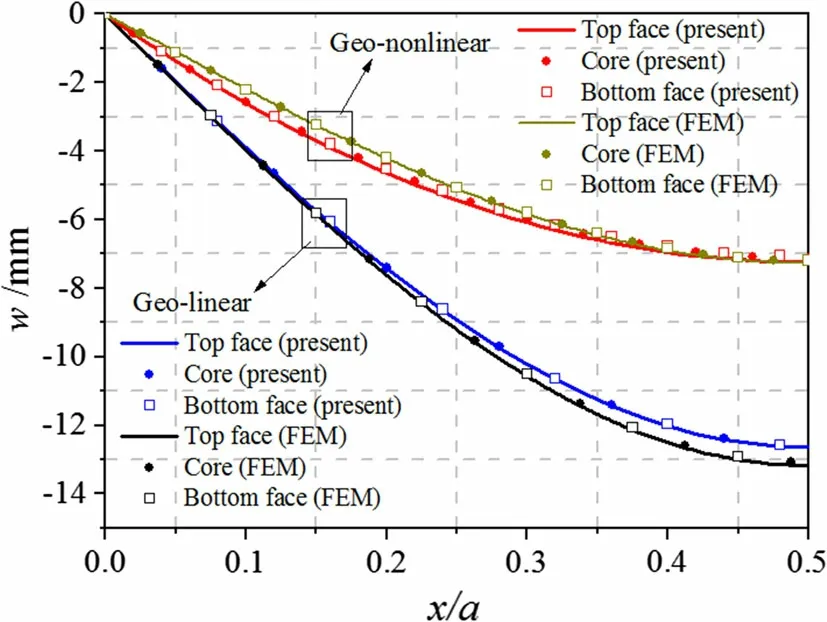
Fig.6 Transverse displacements at midfaces of sandwich layers from linear EHSAPT,geometric nonlinear EHSAPT,and finite element simulation

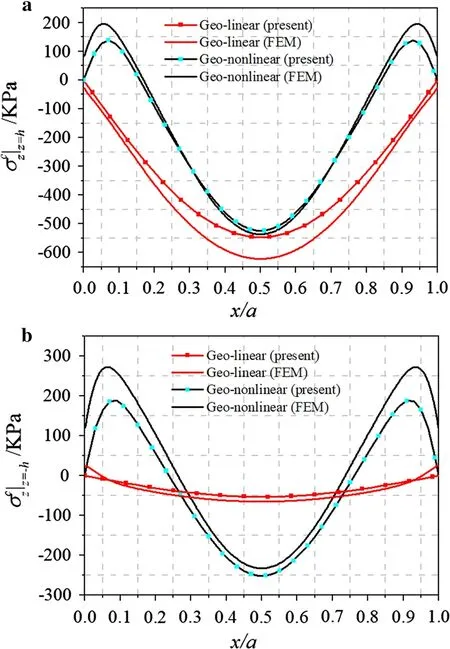
Fig.7 Distributions of normal stresses at interfaces a z =h,b z =-h along x-axis from linear EHSAPT,geometric nonlinear EHSAPT,and finite element simulation

The distributions of the transverse normal stress σczand shear stress τczxat the interface z =h along the longitudinal direction are plotted in Fig.7a.The linear analysis predicts that σczreaches its peak at the center,followed by a decrease from the midspan to the ends. In the geometric nonlinear analysis,the stress fluctuates along the panel.A similar distribution of σczon the interface z = -h can be observed in Fig.7b,but the magnitude of the normal stress is much larger in the geometric nonlinear analysis than in the linear case.

Fig.8 Distributions of shear stresses at midface of core along x-axis from linear EHSAPT,geometric nonlinear EHSAPT,and finite element simulation

The shear stress τczxshows an antisymmetric distribution on the plane x =a/2(Fig.8).The magnitude is lower in the geometric nonlinear analysis compared with linear EHSAPT.In addition,the FEM supports the EHSAPT results well.It is observed that geometric nonlinearity makes a positive contribution to the normal stress and total strain energy but a negative contribution to the shear stress,in the current analysis.

4.3 Geometric and material nonlinearities

To consider the geometric and material nonlinearities simultaneously, a sandwich beam with an arbitrary stress-strain relationship in the core is investigated.Due to the lack of open literature on the mechanical response of sandwich beams with arbitrary stress-strain relations in the core, the results of the proposed nonlinear EHSAPT are compared with those of the finite element model.The geometry follows the example in Ref. [17], having total length a = 300 mm, width d = 300 mm, face thickness ft= fb= 1 mm, and core thickness 2h = 30 mm. The core is made of polyurethane foam,and the material properties are obtained from uniaxial compression tests [27]. The face sheets are made of spring steel with elastic modulus of 200 GPa. A set of MATLAB programs is coded to fit the experimental stress-strain curve using a polynomial fitting method.As seen in Fig.9,when the fitting order is equal to 5,the two curves are very close.

In the three-point bending boundary condition,the sandwich beam is subjected to a transverse line load at the midspan of the top face.A finite element model was established using OptiStruct to verify the theoretical results.The relation between the load and the vertical displacement at the center of the top face is depicted in Fig.10.The theoretical results show good agreement with the FEM calculation.In the plastic region, the difference increases slightly with increasing load. The reason is because the normal stresses are assumed to be elastic in the present EHSAPT for computational efficiency,and only the nonlinear response in the shear stress is considered, while the nonlinear response in the normal stress is included in the FEM.

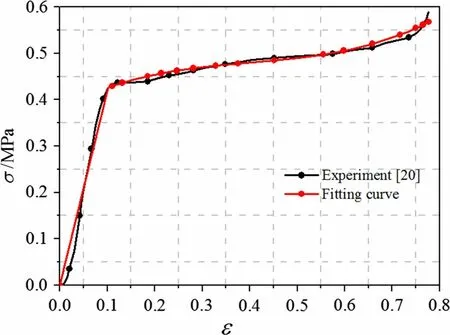
Fig.9 Comparison of curve obtained by polynomial fitting with experimental curve from Ref.[27]

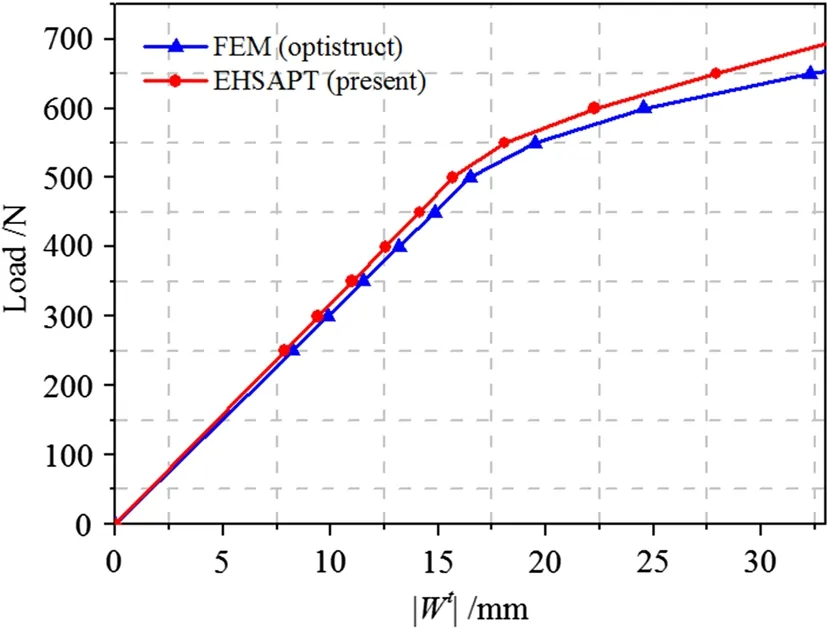
Fig.10 Load-displacement response at center of top face sheet by three-point bending test from finite element and present theoretical model.The sandwich beam consists of two spring steel face sheets and a PU foam core

When a transverse line load L =-550 N is applied,the theoretical and numerical results for the vertical displacement at the top face along the panel are shown in Fig. 11.The EHSAPT results approach those of the FEM closely,with a maximum difference of approximately 7.7% at the center.

The variations of the normal stresses at the face-core interfaces along the longitudinal direction are shown in Fig.12.On the upper interface,the absolute value of the normal stress reaches its peak at the center, and sharply increases in the vicinity of the ends.Asimilar distribution of the normal stress can be found on the lower interface.It can thus be concluded that the normal stress along most of the panel except for the two ends is below the yielding value,so the linear assumption for the normal stress in the current EHSAPT analysis is acceptable.

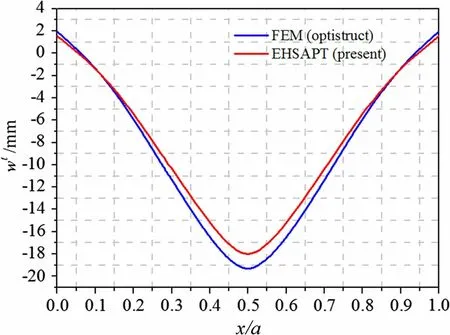
Fig.11 Comparison of FEM and EHSAPT results of vertical displacement of face sheets for a sandwich beam under three-point bending loaded by a transverse line load L =-550 N

Fig.12 Normal stresses in the interfaces along the longitudinal direction under transverse load L =-550 N:a top face-core interface,b bottom face-core interface

The distribution of the shear stress at the middle of the core along the panel is shown in Fig.13.The shear stresses show an approximately sinusoidal distribution along the longitudinal direction.The shear stresses are larger than the yielding values in the vicinity of the center.The finite element results support the EHSAPT well.

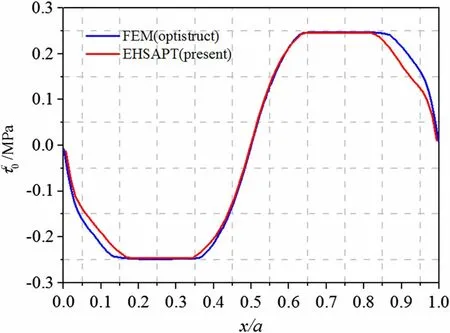
Fig.13 Shear stresses in the middle of the core along the panel under transverse loading L =-550 N

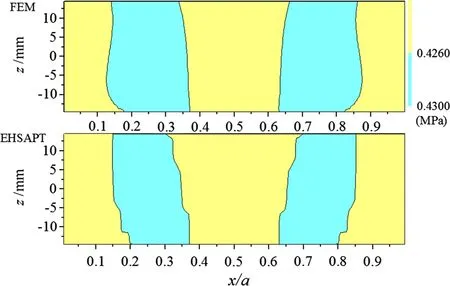
Fig.14 Contours of von Mises stresses in a cross section of the core in the FEM calculation and present EHSAPT

The contours of the von Mises stress in a cross-section of the core are displayed in Fig.14.In the yellow regions,the von Mises stresses are below the yielding stress,and in the light-cyan regions, the core yields. In the current analysis,plastic behavior occurs in the vicinity of the midspan and through the thickness of the core.The EHSPAT results agree well with the finite element simulations.

5 Conclusions

The nonlinear response of sandwich beams is investigated using EHSAPT to estimate the influence of geometrical and material nonlinearities on their mechanical properties.The strain-displacement relationships in the sandwich layers follow the nonlinear Green-Lagrange type to indicate the geometric nonlinearity.The material nonlinearity is indicated by a piecewise function obtained by fitting experimental data from tension or compression tests. The stress-strain curves can be arbitrary and are not limited to the bilinear type generally analyzed in open literature. To obtain accurate results, a Ritz-based method is applied. The sandwich panel is divided into multiple elements,with nine degree of freedoms at each node. The displacements in each element are indicated by using Lagrange and Hermite polynomial functions as trial functions. When the nonlinear governing equations are derived,a modified Newton-Raphson iterative technique is applied to obtain the results.In the elastoplastic core, the plastic region is determined by an iterative calculation. The fully elastic governing equations are solved to detect the initial plastic region, following an iterative correction of the plastic borders.The present theoretical model of EHSAPT is compared with the analytical one and finite element simulations to verify its accuracy.

The geometric nonlinear EHSAPT well captures the stress stiffening behavior of sandwich beams with simply supported ends. The effect of the geometric nonlinearity in the face sheets on the displacement response is more significant for large stiffness ratio of the face sheets to the core. The distributions of transverse displacements and normal and shear stresses reveal that the influences of geometrical nonlinearity on the mechanical response of sandwich beams strongly depend on the load size and should not be ignored.Additionally, geometric nonlinearity decreases the shear stress but increases the normal stress in the core.

A sandwich beam with an elastoplastic core under threepoint bending boundary conditions is investigated to reveal the material nonlinearity. The experimental stress-strain curve is closely matched by the polynomial fitting technique when the fitting order is sufficiently large. The mechanical response of the displacement and normal and shear stresses is calculated by the present nonlinear EHSAPT. In addition,contours of equivalent von Mises stress in a crosssection of the core are plotted to show the elastic and plastic regions.Comparisons with FEM suggest that the present theoretical model to describe the stress-strain relation using a polynomial fitting technique is applicable for predicting the nonlinear mechanical response of sandwich beams by considering the geometric and material nonlinearities simultaneously.

Acknowledgements This work was supported by the National Natural Science Foundation of China(Grant 11432004).

Appendix

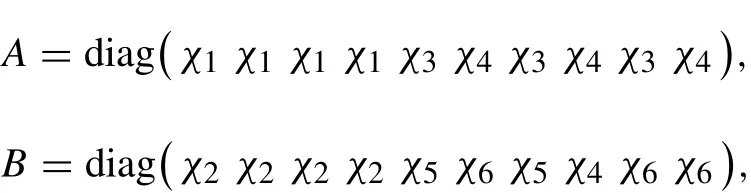
with