Nonlocal thermo-elastic constitutive relation of fibre-reinforced composites

Linjuan Wang·Jifeng Xu·Jianxiang Wang·Bhushan L. Karihaloo

Abstract The effective properties of composite materials have been predicted by various micromechanical schemes. For composite materials of constituents which are described by the classical governing equations of the local form, the conventional micromechanical schemes usually give effective properties of the local form. However, it is recognized that under general loading conditions,spatiotemporal nonlocal constitutive equations may better depict the macroscopic behavior of these materials.In this paper,we derive the thermo-elastic dynamic effective governing equations of a fibre-reinforced composite in a coupled spatiotemporal integral form.These coupled equations reduce to the spatial nonlocal peridynamic formulation when the microstructural inertial effects are neglected.For static deformation and steady-state heat conduction,we show that the integral formulation is superior at capturing the variations of the average displacement and temperature in regions of high gradients than the conventional micromechanical schemes. The approach can be applied to analogous multi-field coupled problems of composites.

Keywords Nonlocal theory·Thermoelasticity·Composite materials·Constitutive equations

1 Introduction

The overall responses of various composite materials under external stimuli are usually predicted based on their effective properties. For composite materials composed of constituents that are governed by classical linear constitutive relations,predictions of the effective elasticity tensors under mechanical loading and effective conductivity tensors under conduction have been well studied. These effective tensors are then used in the governing equations of the homogenized materials. These governing equations in turn exhibit the same form as those for the constituents. For example,when the constituents are governed by the classical Navier equation of motion or the Fourier equation of heat condition, the homogenized composite materials are regarded as being governed by the equations of the same type.Hashin[1]pointed out that“this simplest approximation is adequate for most engineering problems”, but “the situation is different for dynamic problems”,and“for very high stress and strain gradients”.As a matter of fact,a series of generalized continuum models have been proposed to take into account the microstructural effect of heterogeneous materials,which can be roughly divided into two categories.

The first category is the phenomenological nonlocal continuum theories proposed by directly introducing weight functions or additional high-order gradient terms into constitutive relations, such as Mindlin’s theory, Eringen’s theory,the strain gradient theory,the stress gradient theory,and the micropolar theory, which have been reviewed in Ref. [2-4].The recent experimental results of Rueger and Lakes[5]demonstrate that the polymer lattices show a strong effect of Cosserat elasticity.Most of the proposed nonlocal continuum theories are spatial nonlocal with succinct forms,and are convenient for application to capturing the size effects and dispersion phenomena in composite materials.However,the determination of the weight functions and additional parameters of high-order gradient terms has not been completely resolved and remains a challenging issue.

The second category is the resultant effective models for composite materials derived by considering the microstructures. For example, Drugan and Willis [6] have developed the nonlocal constitutive equations of composite materials that incorporate the spatial gradients of the average strains.Bigoni and Drugan [7] find that from the viewpoint of overall behaviour,a composite material containing soft inclusions can be more accurately represented by a homogeneous Cosserat material than by an effective Cauchy material,when the material is subjected to nonuniform stressing.Compared to statics,the dynamics of composite materials is less studied,but has been attracting much attention,in particular,due to increasing interest in acoustic metamaterials[8].It has been shown that the dynamic governing equations of composite materials exhibit spatial and temporal non-locality[9-11].

Recent studies have shown that the above two categories can be connected with each other.For example,Silling[12]demonstrates that the effective governing equation of the average displacement of a unidirectional composite under uniaxial stress can be expressed in the spatial nonlocal form of Eringen’s theory,and can further approximate to the spatial nonlocal form of the peridynamic theory proposed by Silling in 2000 [13]. Silling [12] also emphasizes that though the constituents of the composite are described by the classical local elasticity,non-locality emerges in modelling the composite using the average field quantities. We note that this connection provides an approach for addressing the challenge in the first category,i.e,the determination of additional parameters in the phenomenological nonlocal theories.This is one of the motivations for the present study of the effective dynamic governing equations of composites under thermomechanical loading.

Today, the thermal-mechanical behaviour of composite materials under transient and high-gradient temperature is an issue of remarkable importance in aeronautical industry,which is highly relevant to the safety of composite structures,e.g.under thunder strikes.While the response of composite materials under mechanical loadings has been studied extensively,there are few studies of the overall dynamic behaviour of composite materials under multiple coupling fields.Therefore,in this paper,we study the thermo-elastic dynamics of a unidirectional composite material using a cylindrical unit cell under coupled thermo-mechanical loading. We derive the average deformation and temperature fields, and show that they can all be expressed in coupled integro-differential forms.These integro-differential forms contain coupled spatiotemporal non-locality,and can correspond to the results of the peridynamic theory.We then apply the theoretical formulations to widely used composite materials,and show that the average displacement and temperature fields in the regions of high gradients are drastically different from the predictions of the conventional micromechanical schemes,and the nonlocal theory gives much more accurate predictions.

2 Fully coupled nonlocal framework

Wang et al. [11] have presented a general spatiotemporal nonlocal constitutive formulation for elastodynamics of composite materials under mechanical loading,and analysed the dispersion relations of a unidirectional fibre-reinforced composite material as an example. The composite material is represented by a composite cylinder model where a fibre of radius rfis embedded in a concentric matrix shell of an outer radius rm, and the composite cylinder is under mechanical loading in its longitudinal direction. In this work, we consider the same model,as shown in Fig.1a;however,we apply both an axial stress and a heat flux to the ends of the composite cylinder, and establish the coupled thermo-mechanical governing equations. Both the fibre and matrix satisfy the governing equations of classical thermo-elastic dynamics

and the constitutive relations for linear materials

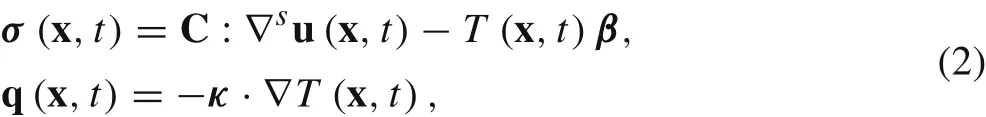
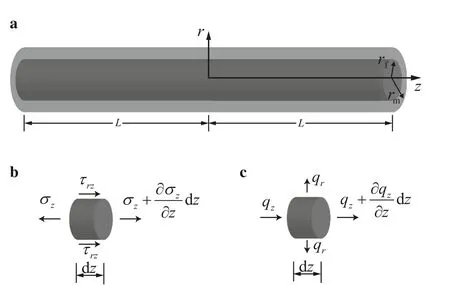
Fig. 1 a Composite cylinder model, which has been widely used to calculate the effective properties of unidirectional fibre-reinforced composites(e.g.Refs.[1,11]).b Stresses exerted on an infinitesimally small segment of the fibre. c The thermal fluxes of an infinitesimally small segment of the fibre

in which u(x,t) and T (x,t) denote the displacement and temperature of the material point x at time t, respectively;ρ and cvare the mass density and specific heat capacity,respectively;σ(x,t)is the stress tensor;q(x,t)is the heat flux;β is the thermal modulus tensor;b(x,t)and hs(x,t)are body force and heat source densities, respectively; C is the stiffness tensor;κ is the heat conductivity tensor;∇sdenotes the symmetric gradient operator. Throughout this paper, a dot(˙)over a symbol denotes differentiation with respect to time,and a prime(′)represents differentiation with respect to a spatial coordinate.The fibre and matrix in the composite are assumed to be isotropic materials. The Young’s moduli of the fibre(f)and matrix(m)are denoted by Efand Em,the thermal conductivities by κfand κm,the thermal moduli by βfand βm,the mass densities by ρfand ρm,and the specific heat capacities by cvfand cvm,respectively.Thus,we shall derive relations for the overall behaviour of the composite cylinder in the longitudinal direction,in a different way from the classical micromechanics.

2.1 Displacement field

A usual cylindrical coordinate system is set for the composite cylinder model where the z-axis coincides with the axis of the fibre such that the z =±L correspond to the two ends of the cylinder.We consider the case when the ends of the composite cylinder are subjected to an axial stressand a heat fluxsimultaneously. The outer surface of the composite cylinder is free of stresses,and the heat flux in the radial direction is zero at the surface; the fibre and matrix are perfectly bonded so the displacement and temperature are continuous at the fibre-matrix interface.For pure mechanical loading, Wang et al. [11] have considered the stress and displacement fields using the shear-lag model.Here,we will include the thermal effect based on the coupled thermomechanical governing Eq.(1).

Using the shear-lag model of Gao and Li [14], the displacement um(r,z,t)of the matrix and uf(z,t)of the fibre in the z-direction is connected by the relation[11]

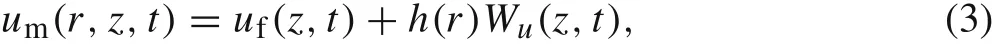
in which

where um(r,z,t), uf(z,t) and Wu(z,t) are unknown functions to be determined.Because the derivations only refer to the Hooke’s law for the shear stress which is not affected by the thermal effect,the displacement Eq.(3)is applicable to the thermo-elastic field.

We are concerned with the average longitudinal displacement over the cross section of the composite cylinder,defined as

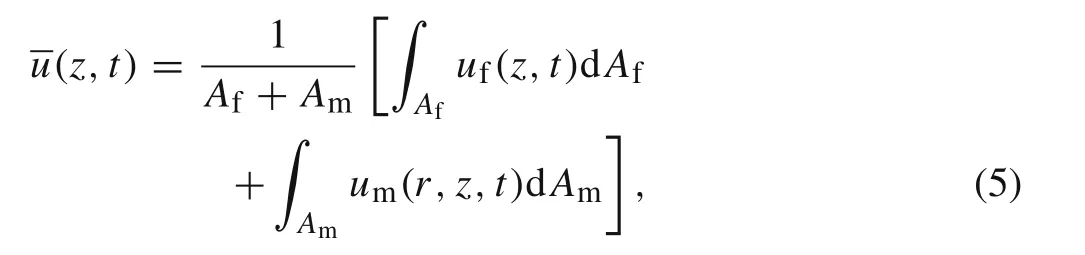
where Afand Amare the cross-sectional areas of the fibre and matrix,respectively.Substituting Eq.(3)into Eq.(5)gives

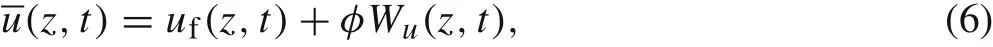
in which

By considering the motion of an infinitesimally small segment of the fibre as shown in Fig.1b,we obtain the equation of motion of a unit length of the fibreρf¨ufAfin which τrz|r=rfis the shear stress on the interface of the fibre and matrix. Based on the constitutive relations in Eq. (2) and the displacement field in Eq. (3), we can obtain σz=andμmh′(rf)Wu(z,t) in which Tfis the temperature field of the fibre and μmis the shear modulus of the matrix. Then,the equation of motion of a unit length of the fibre can be expressed as

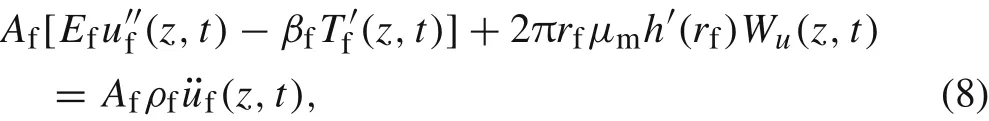
in which the second term on the left hand side represents the resultant force of the shear stress applied on the interface.Replacing ufin Eq.(8)by Eq.(6),we obtain a second-order differential equation with respect to Wu(z,t)

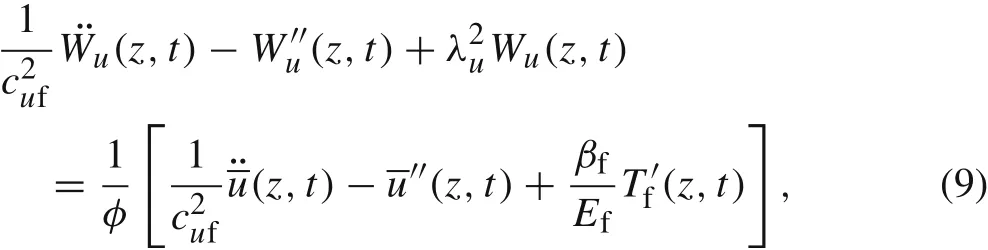
in which

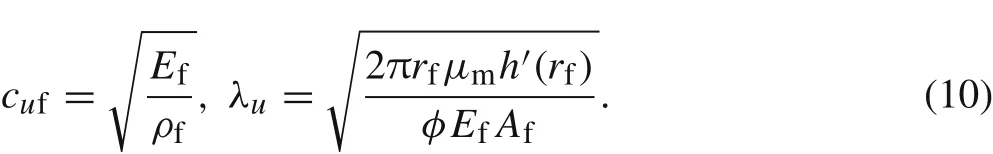
The left hand side of Eq.(9)is the same as that of the equation for the pure mechanical loading in the work of Wang et al.[11],but the right hand side includes the effect of the temperature.By the Green’s function method,the general solution of Eq.(9)can be expressed as

in which the symbol “*” represents the convolution with respect to space and time, which is a spatiotemporal integral operation

where f and g represent two arbitrary functions. Guin Eq. (11) is a function of z and t, that is, Gu= Gu(z,t),which is the solution of the following equation

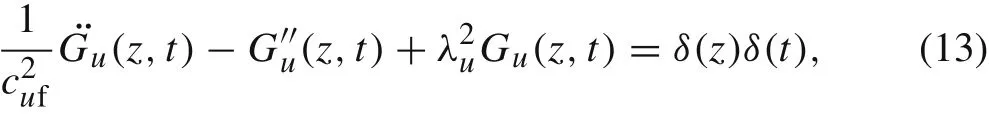
where δ(z)and δ(t)are the Dirac functions with respect to z and t,respectively.From Ref.[11],we know that

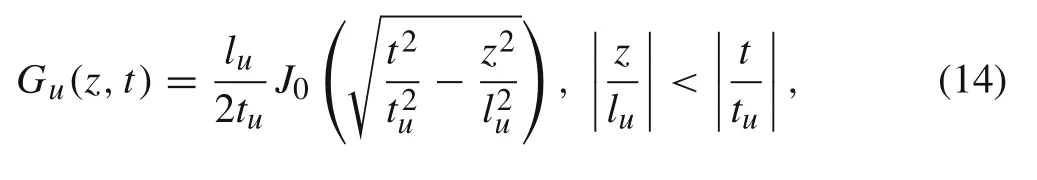
where

are the characteristic length and characteristic time of the composite,respectively.Thus the unknown function Wu(z,t)can be determined by substituting Eq.(14)into Eq.(11).

Now,we calculate the average longitudinal normal stress of the composite cylinder

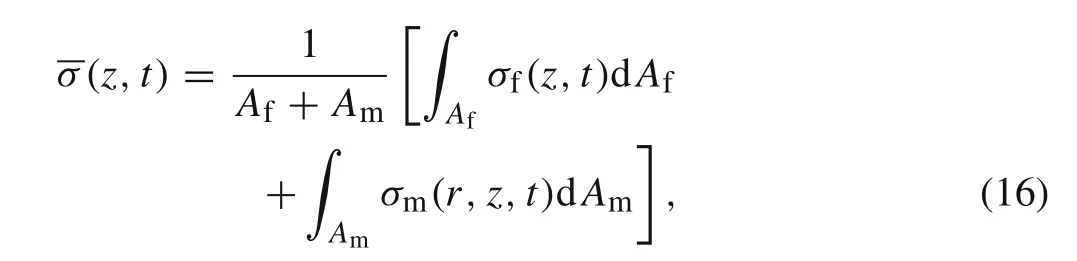
where σf(z,t)and σm(r,z,t)denote the normal stresses(in the z-direction)on the cross sections of the fibre and matrix,respectively.Using the Hooke’s law,we obtain

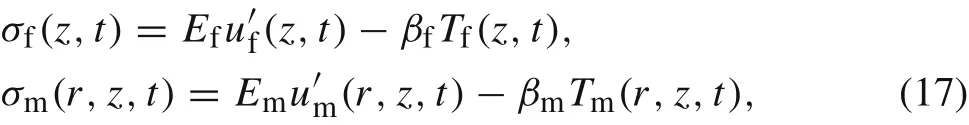
in which Tm(r,z,t) is the temperature field of the matrix.Substituting Eq.(17)into Eq.(16)leads to

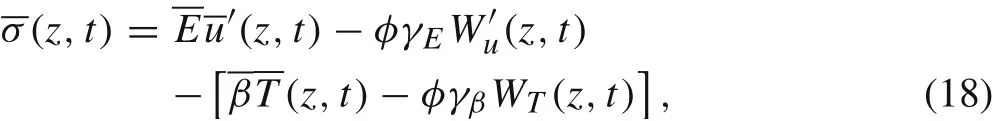
whereT(z,t)is the average temperature over the cross section of the composite cylinder and defined below in Eq.(35);WT(z,t)is related to the temperature field and defined below in Eq.(34),and

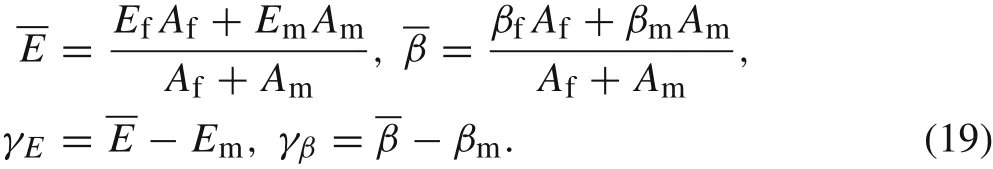
Similarly, we introduce the average inertia force over the cross section of the composite cylinder as

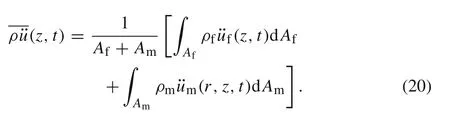
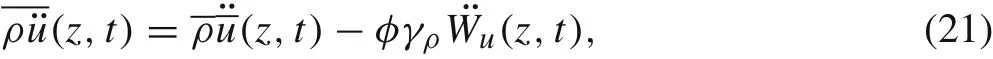
wher e

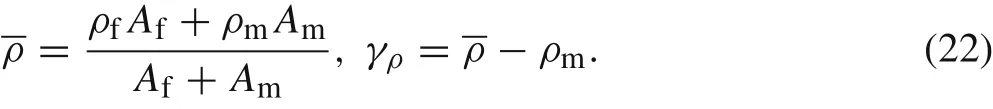
We assume that the body force is independent of r, i.e.,b(z,t).Then,the equation of motion of the composite cylinder taken as a homogenized medium is expressed in terms of the average quantities and the body force as

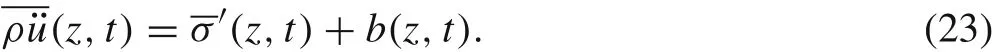
Substituting Eqs.(18)and(21)into the above equation leads to

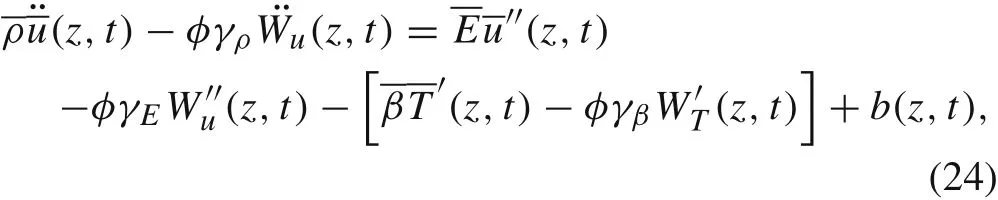
in which W′′ucan be determined by Eq.(11)as

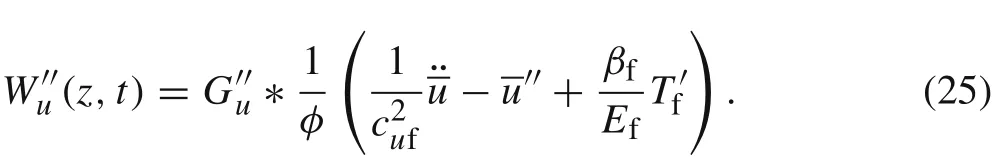
Using integration by parts, the above equation can be expressed as

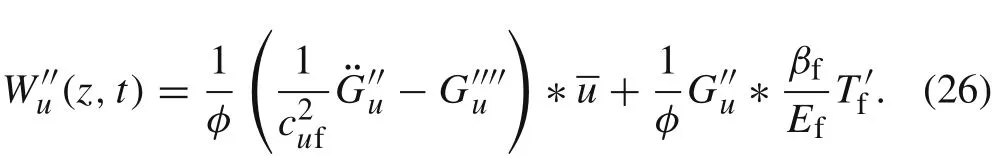
From Eq.(13),we can obtain

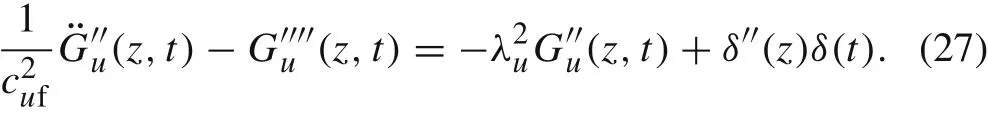
Substituting Eq.(27)into Eq.(26)leads to

Following the lines of the derivations from Eq. (25) to Eq.(28),we can also obtain

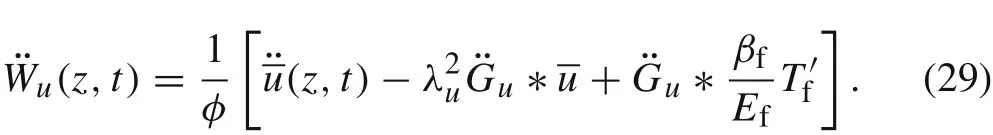
Substituting Eqs.(28)and(29)into Eq.(24)yields the following equation of motion in terms of

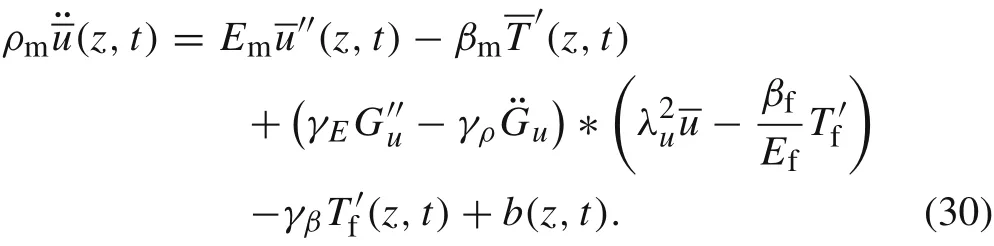
2.2 Temperature field

For heat conduction in the composite cylinder,the boundary conditions are

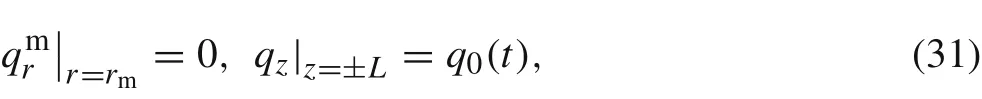
and the interface conditions are

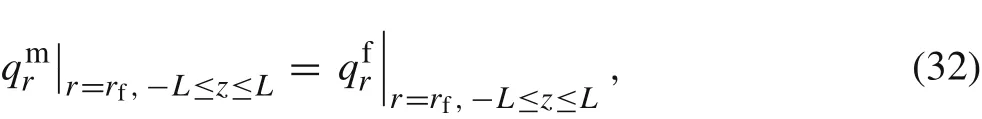
in which qrand qzare components of the heat flux q in the radial and axial directions, respectively. Following similar derivations to those for the displacement field,the temperature field can be expressed as

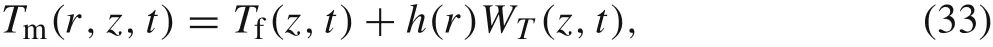
in which h(r)is the same as that in Eq.(4),and

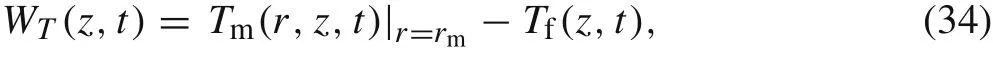
where Tm(r,z,t), Tf(z,t)and WT(z,t)are unknown functions to be determined. The average temperature over the cross section of the composite cylinder is

Substituting Eq.(33)into Eq.(35),we obtain

in which φ is the same as that in Eq.(7).

By considering the thermal energy balance of an infinitesimally small segment of the fibre as shown in Fig. 1c, we obtain the heat conduction of a unit length of the fibrein whichis the heat flux from the fibre to the matrix through their interface.Based on the constitutive relation in Eq.(2)and the temperature field in Eq.(33),there are qz= -and. Thus the heat conduction equation of a unit length of the fibre can be expressed as

in which the second term on the left hand side represents the total thermal energy per unit length transferred from the matrix to the fibre through their interface.Replacing Tfin the above equation by Eq.(36)leads to the equation for WT(z,t)

in which

By the Green’s function method, the general solution of Eq.(38)can be expressed as

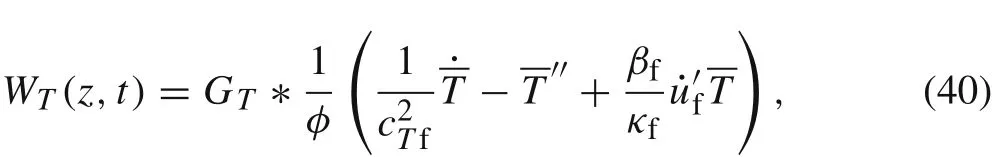
in which GT(z,t)is the solution of the following equation

The average heat flux over the cross section of the composite cylinder is

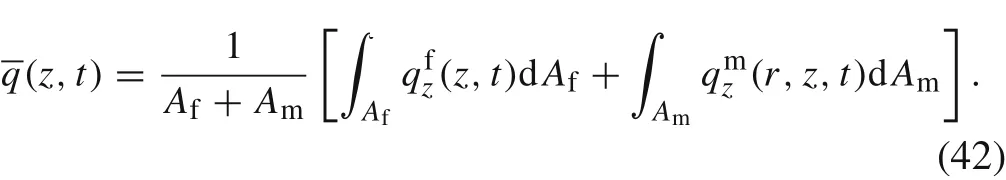
With

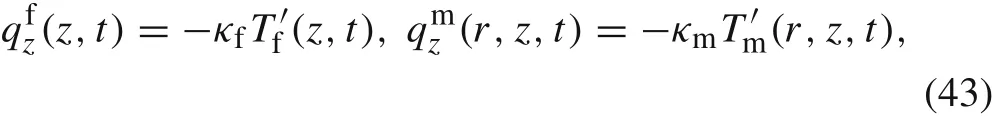
we obtain

where

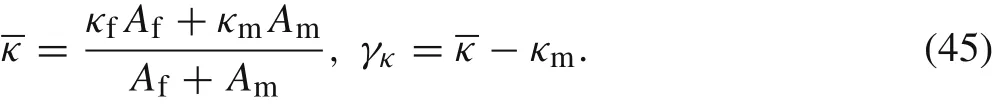
Similarly,by the definition of the average of the rate of thermal energy

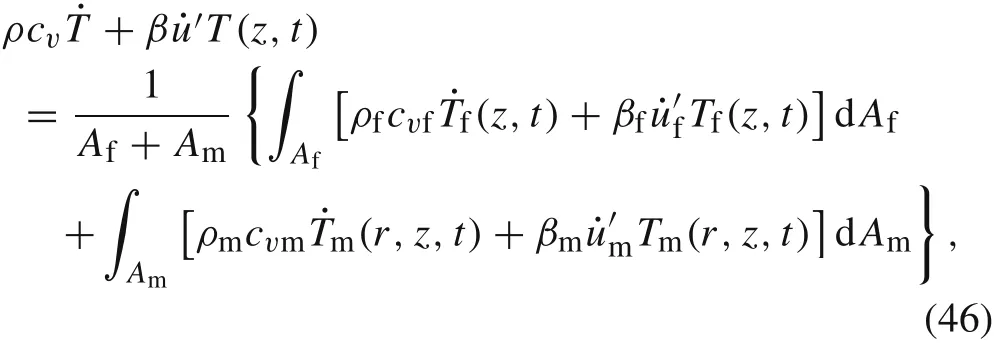
we have

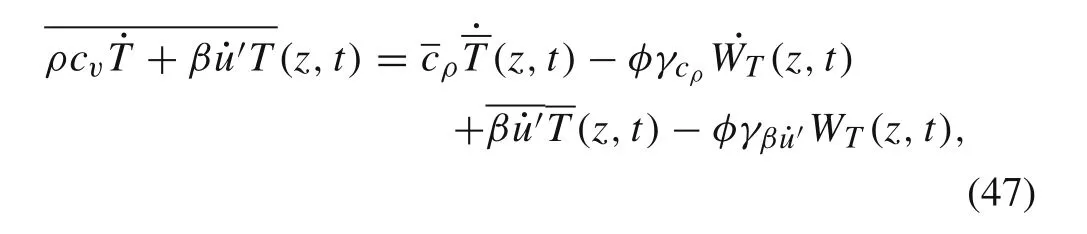
where

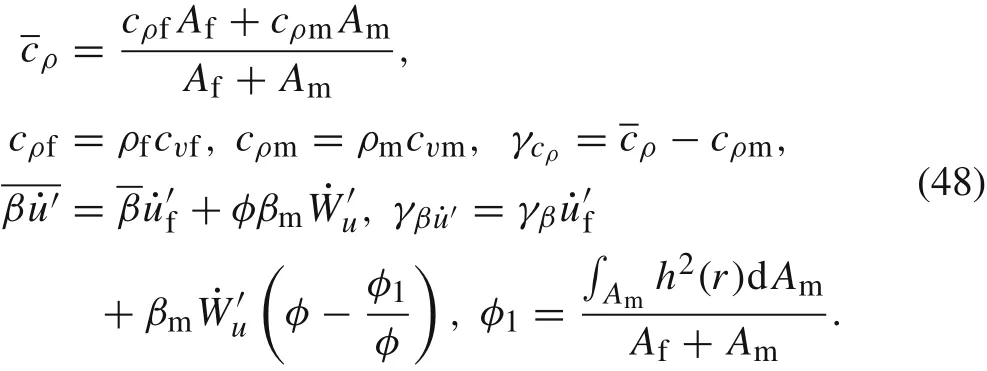
With the heat source density hs(z,t)independent ofr,substitution of Eqs.(44)and(47)into the heat conduction equationfor the composite yields

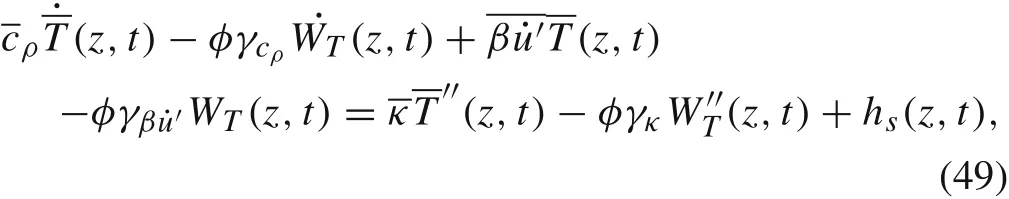
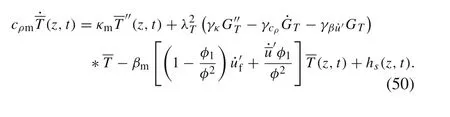
Equations(30)and(50)constitute the governing equations of the thermo-elastic dynamics for the average displacement and average temperature fields, which include fully coupled thermo-elastic effect,and more importantly,the coupled spatiotemporal nonlocal effect. It is noted that though the constituents of the composite are all classical thermo-elastic materials governed by differential equations in Eq. (1), the coupled spatiotemporal non-locality arises naturally in the governing equations of the average field quantities. In particular, the temporal non-locality in Eq. (50) indicates that the average temperature is related to its history,which resembles the phase lags introduced in non-Fourier heat conduction models[15-18].It means that though the constituents of the composite obey the Fourier law,the average temperature field exhibits a non-Fourier characteristic.

The coupled term T β : ∇˙u in Eq. (1) makes Eq. (1) a nonlinear equation with respect to u and T, which leads to the coupled terms of ufand Tfin Eqs. (30) and (50). In the classical local thermo-elastic theory, for simplification,the coupled term T β :in Eq. (1) is commonly made to be T0βin which T0is the initial temperature of the material.T0mand T0fare the initial temperature of the matrix and fibre,respectively.Introducing this simplification,we can simplify Eq. (47), and express the governing Eqs. (30) and(50)as

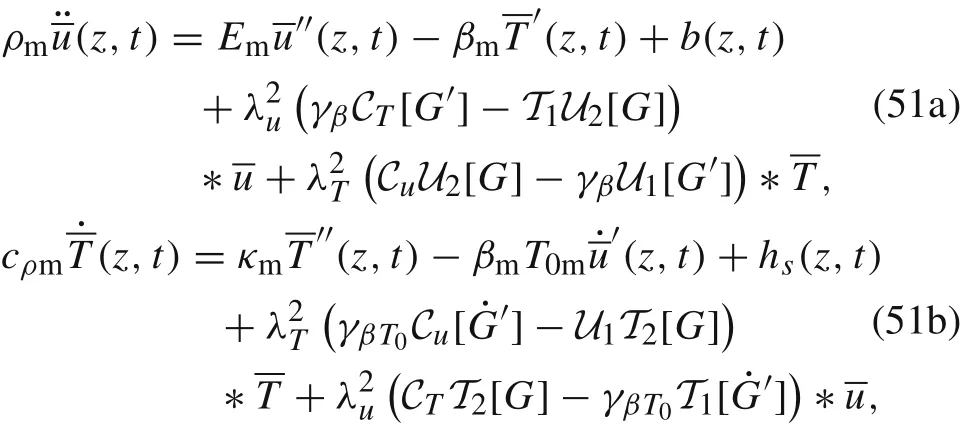
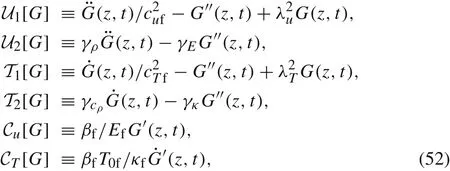
3 Coupled thermo-elasticity without inertial effects

In this paper,inertial effects refer to the following two cases:the first one is the microstructural inertial effects,that is,the terms on the right hand sides of Eqs.(8)and(37);the second one is the heterogeneity of inertia,that is,the mass densities and specific heat capacities of the fibre and matrix are different.In this section,we focus on the thermo-elastic coupling,neglecting the inertial effects of the above two cases, similar to the treatments in Refs. ([11,12]). This simplification results that the right hand sides of Eqs.(8)and(37)are equal to zero,and there are ρm= ρf≡ρ0and cvm= cvf≡cv0where ρ0and cv0are constants.In this case,the integrations with respect to time in Eqs.(11)and(40)are absent.Repeating the derivations of Eqs. (51a) and (51b), one can obtain the governing equations as follows

in which the symbol ◦denotes the spatial convolution andand GT(z,t) are the Green’s functions of the following second-order differential equations with respect to Wu(z,t)and WT(z,t),respectively,

which are obtained from Eqs.(9)and (38)with the inertial terms neglected.Thus,Gu(z,t)and GT(z,t)are

The governing Eq.(53a)for the displacement can be further expressed as

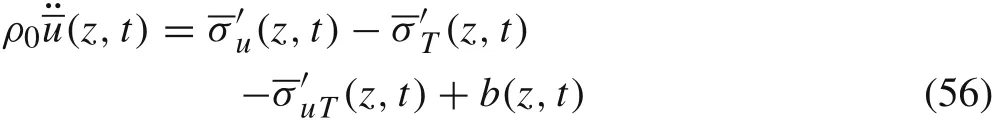
with

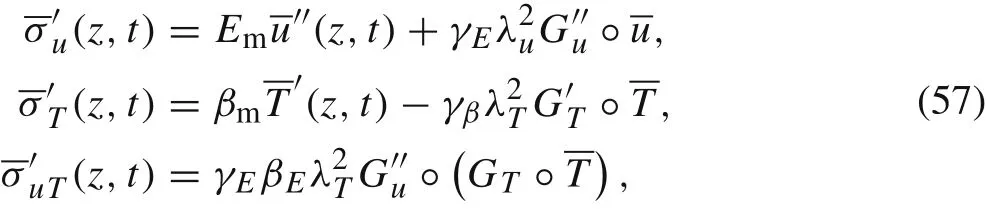
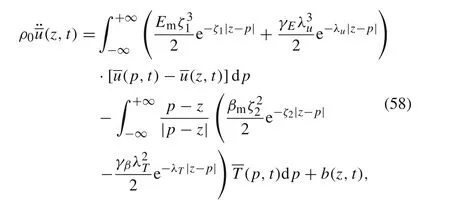
in which ζ1and ζ2are large constants.

Equation(58)is an integral form of the displacement field and does not involve any spatial derivatives of the displacement and temperature fields,which is consistent with the idea of the peridynamic theory originally developed by Silling[13] to facilitate the treatment of discontinuous problems.Actually, Eq. (58) has the same form as the equation of motion of the peridynamic thermo-mechanical theory proposed by Oterkus et al. [19] who introduce the concept of the state-based peridynamic theory into irreversible thermodynamics and obtain the governing equation similar to the derivation of the classical thermo-mechanical equations.Our derivation of Eq. (58) is different from that in Ref. [19];we derive the equation by homogenization of a composite with microstructures.The parameters in Eq.(58)are explicitly determined by the microstructural information.Further,when the mechanical displacement and the temperature field are decoupled, the governing Eq. (58) of the average displacement can approximate to the formulation of the bond-based peridynamic theory[13].

Similarly,neglecting the last term of Eq.(53b)and using the approximation method in Ref. [12], Eq. (53b) can be expressed in the integral-type nonlocal form

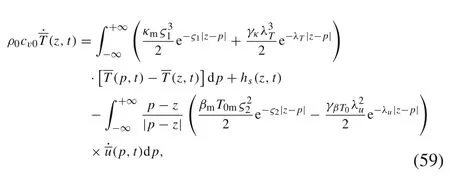
where ς1and ς2are two large constants.Equation(59)has the same form as the heat conduction equation in Ref.[19],and makes two advances on previous research. First, the integral form is obtained based on the established classical theory.As emphasized by Silling[12],the non-locality naturally emerges in modelling the composites using the average field quantities,though the constituents are all classical local media.Second,a mechanism-based exponential kernel function is derived for the first time,which is supplementary to the currently used power-law kernels[20-23].In addition,if β = 0,Eq.(59)reduces to that of the peridynamic thermal diffusion model presented by Oterkus et al. [21]. Recently,some other generalized thermo-elastic models with nonlocal effects have also been proposed[24,25],and it is possible to establish the connections between our proposed model and them.Moreover,the methodology of the present work may be applied to derivation of overall governing equations of heterogeneous media whose constituents obey mathematically analogous governing equations, such as chemo-mechanical coupled cases[26].

4 Examples of deformation and temperature fields

In this section,we apply the above nonlocal theoretical formulation to some commonly-used composites,and calculate the displacement and temperature. We compare the results with the finite element numerical computations and the results predicted by the classical micromechanical scheme to show the advantages of the nonlocal theory.

4.1 Displacement

In the first example,we neglect the thermal effect on deformation and apply uniform stress σ0on the two ends of the composite cylinder, as shown in Fig. 2. Without the body force,the nonlocal governing equation for the static problem can be obtained by simplifying Eq.(56)and expressed as

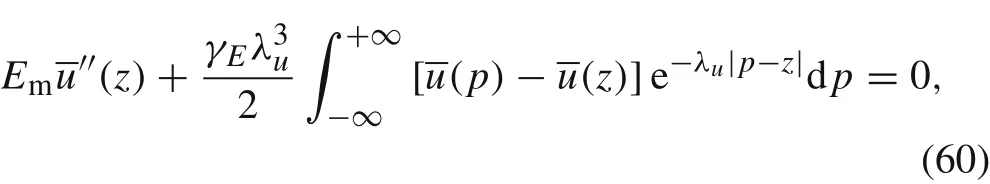
while the classical governing equation is

In order to get analytical solutions for the above static problem,the one-dimensional problem is equivalent to an infinite bar of a uniform cross section with σ0exerted at z = ±L.By the Green’s function method[27],the analytical solutions for the local and nonlocal equations are

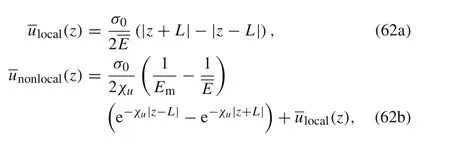
As the second example, we assume that the temperature of both the fibre and matrix is increased by Tc.Equation(56)indicates that the temperature increase Tcwill cause a uniform stress σ0=in the homogenized bar if it is constrained at the two ends, which is consistent with the classical homogenization.Thus the problem is equivalent to applying the uniform stresson the two ends,and can be described by the nonlocal Eq.(60)or classical Eq.(61)with the boundary conditions σ(z = ±L) =Therefore,the analytical solutions for Eqs. (60) and (61) with the boundary conditions σ(z = ±L) =can be directly obtained,again,using the Green’s function method[27]

We consider two kinds of composite:E-Glass/MY750 and AS/Epoxy. Their material parameters are listed in Table 1.The volume fraction of the fibre in both composites is 60%.The relationships between the normalized position z/L and axial displacementare shown in Fig. 2, where the results predicted by the classical local micromechanical scheme and the nonlocal approach are compared with the results computed using the finite element method (FEM). The FEM results are obtained with the commercial software ANSYS by discretising the fibre and matrix into three-dimensional elements (Plane 182 as an axisymmetric element). In comparison with the analytical micromechanical scheme and the nonlocal approach,the FEM results are purely numerical and used as a sort of benchmark,but they are otherwise not necessary from the point of view of predicting the overall properties of composites.

The nonlocal formulation agrees very well with the FEM in the whole region,whereas the classical theory agrees well with the FEM in the region away from the ends,and it deviates significantly from the FEM and the nonlocal theory in the region close to the ends. The effective elastic modulusin Eq. (62a), predicted by the classical micromechanical scheme,is regarded as a very accurate prediction of the longitudinal modulus of the composite cylinder, subject to the Saint-Venant’s principle[29],which means that the relation in Eq. (62a) is accurate in the region away from the ends.Figure 2 confirms this.However,the nonlocal formulation,which is also simple,is accurate in the whole region,including the ends.The phenomenon that the effective elastic property of the boundary region is different from that of the region away from the boundary is regarded as the “boundary effect” in the prediction of the effective properties of composites [6], which has been attracting much attention in the classical micromechanics of composites[30,31].The nonlocal formulation successfully and elegantly captures the“boundary effect”for this case,whereas complicated computations or numerical computations may be needed to achieve the same accuracy in the formalism of classical micromechanics.

Based on the analytical solutions in Eqs.(62)and(63),we can further analyze the effective elastic modulus and coefficient of thermal expansion. According to the definitions of the effective Young’s modulus and coefficient of thermal expansion

in which〈σ〉and〈ε〉are the average stress and average strain over the length of the bar, and 1L is half of the elongation of the bar,we can obtain the effective Young’s modulus and coefficient of thermal expansion for local and nonlocal formulations as

The last formula of Eq.(65b)constitutes the counterpart of the classical Levin’s formula of the local theory [32]. For E-Glass/MY750 composite,there are=0.81E andwhileandfor As/Epoxy composite.

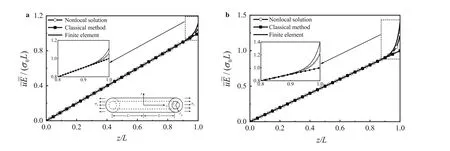
Fig.2 Average displacement field of the composite cylinder model.a E-Glass/MY750.b AS/Epoxy

4.2 Temperature

For the heat conduction problem of the composite cylinder,as the heat source is neglected,the nonlocal governing equation for steady-state heat conduction is

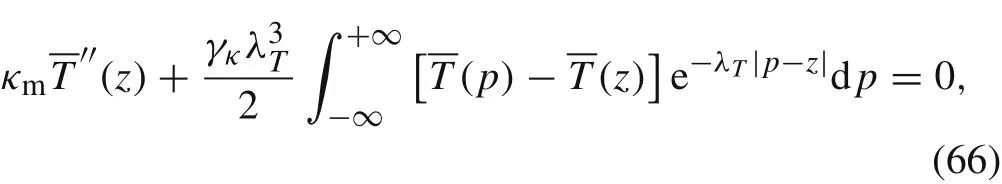
while the classical governing equation is

The two ends of the composite cylinder are subjected to a uniform heat flux q0,as shown in Fig.3.As before,the onedimensional problem is equivalent to an infinite cylinder with heat flux q0at z =±L.By the Green’s function method[33],the analytical solutions for Eqs.(66)and(67)with boundary conditions q(z =±L)=q0are

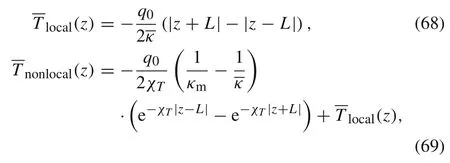
We take two kinds of composite as examples: carbon nanotube (CNT)/polymer and diamond/ZnS, in which the volume fractions of the fibre are 60%.The material parameters are listed in Table 2. The variation of the normalized temperaturewith position z/L is shown in Fig. 3.

We reach similar conclusions to those for the displacement field:thenonlocal formulationis closer to the FEM numerical results;and the nonlocal formulation can accurately capture the“end effect”which increases with increasing κm/κf.Similarly,the effective thermal conductivity can be obtained as

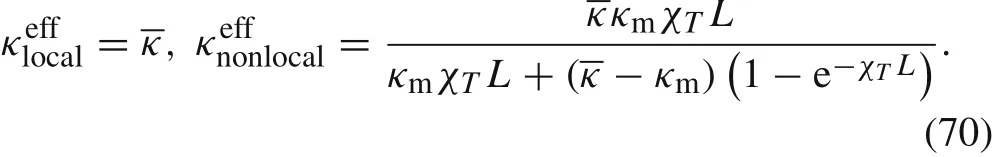
These examples clearly reveal the benefits and advantages of the nonlocal formulation which contains more microstructural information.For both the deformation and temperature fields, the nonlocal formulation successfully describes the“boundary effect”where the average displacement and temperature exhibit higher gradients than a linear function.Silling et al.[36]have mentioned that the decay rates for fluctuation of displacements away from the loading region may be viewed from the point of the Saint-Venant’s principle.However the relationship between the nonlocal description and the Saint-Venant’s principle has not been explored.We show our exploration of this relationship in the Appendix.It is seen that the orders of magnitude of the characteristic length that is obtained from the study of the Saint-Venant’s principle and that of the nonlocal theory are comparable,and their values may be close to each other around a specific volume fraction for the considered material, but they are generally different.

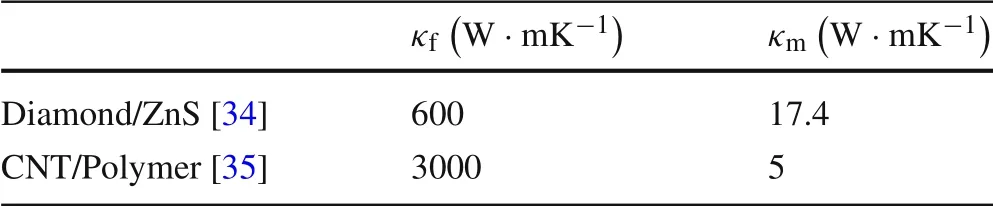
Table 2 Thermal properties of composites

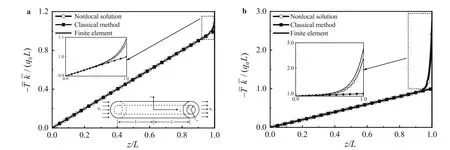
Fig.3 Average temperature field of the composite cylinder model.a Diamond/ZnS.b CNT/polymer

5 Conclusions

The results of this work have two major implications in modelling of composite materials.First,while the dynamic mechanical and conductive behaviour of monolithic materials may be well described by the classical local theories in most cases under external stimuli,the average field quantities of a heterogeneous material may exhibit spatial and temporal non-locality. Although various nonlocal theories for mechanics and conduction have been proposed in Ref.[4], the determinations of the involved materials parameters and the nonlocal interaction functions have always been a challenging issue. The examples of this work provide clear expressions of these parameters and kernel functions in the integral formulations, in terms of the material and geometrical parameters of the composite materials. Second, the spatially nonlocal theory has been applied to modelling multi-field problems of materials, such as the Eringen model for magneto-electro-elastic coupling [37]and the piezoelectric-thermo-elastic problem[38],the peridynamic model for thermo-mechanical coupling [39], and the peridynamic model for electro migration with four coupled physical fields including mechanical deformation,heat transfer, vacancy diffusion and electrical potential distribution [20]. The method of this work may be used to derive the corresponding parameters and functions in the nonlocal formulations based on the mathematical analogy of the problems. In addition, it is noted that the overall mechanical behaviour of composites that are composed of constituents with nonlocal constitutive relations themselves have been studied[40,41];however,we are only concerned with composite materials that are composed of components which obey the classical local constitutive relations in this work. Even for these classical composite materials, the overall dynamic governing equations are different from the conventional one. Further studies can be carried out to investigate the homogenization for composites composed of constituents with nonlocal constitutive relations.

AcknowledgementsL.J. Wang and J.X. Wang thank the support of the National Natural Science Foundation of China(Grants.11872075 and 11890681),and the China Postdoctoral Science Foundation(Grant 2018M641081).

A Appendix:Relation of the nonlocal description to Saint-Venant’s principle

We note that Choi and Horgan [29] have studied Saint-Venant’s end effect for a semi-infinite composite strip in which a material is embedded between two layers of a different material, and the strip is subjected to self-equilibrating loads at the end.This is the structure in the paper of Silling[12], namely, the two-dimensional counterpart of the composite cylinder in the present work. The solutions of the two-dimensional strip are also given by expression (62b),but with χuexpressed as

in which r0is the half width of the composite strip.By the solution of Ref.[29]for a semi-infinite composite strip,the Airy stress function, from which the displacement, strain,and stress can be derived,can be expressed as

where we have used|z-L|to denote the distance away from the loaded end.F is a function of the coordinate in the transverse direction.The solution ofis generally complicated.However, for the case whencan be solved from a transcendental equation as[29]

With Ef/Em=10,the Poisson ratio of the fibre and matrix νf=νm=0.3,anddepend on the volume fraction of the fibre Vfonly.Therefore,we compare the values of χandin Fig.A1,for different values of Vf.In Fig.A1, Lcdenotes 1/andThe orders of magnitude ofand ˆχ are comparable,but the values are generally different,though they are close around Vf≈0.5.

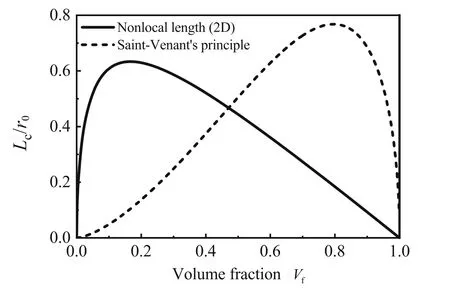
Fig. A1 Characteristic lengths of nonlocal formulation and Saint-Venant’s principle