基于人工神经网络的线损计算及窃电分析

2020-05-06刘超

通信电源技术 2020年24期

刘超

（国网湖南省电力有限公司娄底供电分公司，湖南娄底 417000）

0 引言

随着我国经济的快速发展，电力需求不断上升，但是随着电力需求的快速增长，配电网更加复杂，线损管理更加困难。虽然电力企业通过各种先进技术手段和管理方式增强了电力监管，但难以精准响应窃电行为，窃电情况时常发生，因此需要通过快速定位窃电位置进行更精准的管理。近些年，人工神经网络技术预测相应算法在电力领域有了一定的发展，但现阶段以神经网络为基础的算法对具体的线损管理帮助有限，对特定区域范围内多个可能窃电位置的分析有所欠缺。因此，需建立有关地理区域的负荷和潮流分析模型，并利用窃电模型判定区域内的线损情况和具体位置[1]。

1 人工神经网络原理以及模型的构建

1.1 人工神经网络原理

人工神经网络就是通过模仿人神经元的工作方式，在不同单元之间建立连接，形成以此为基础的模型。人工神经网络主要包括输入层、隐含层以及输出层等结构，如图1所示。

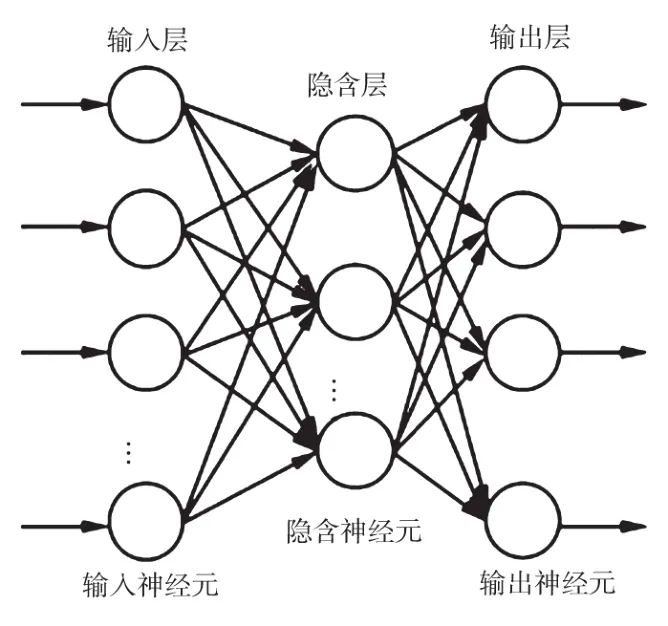
图1 人工神经网络结构模型示意图

输入信号通过两层结构激活函数后输出，同时参照输出误差对每一层神经元连接权值进行调整，以不断降低误差，最终达到设定目标。

1.2 计算及分析模型

为进行线损计算和窃电分析，本文以人工神经网络为基础建立配电网多潮流场景线损计算模型和区域性窃电位置判定模型，计算和分析的数据主要包括潮流、理论线损以及统计线损等。实际操作时，先分析原有数据，确定潮流、理论线损以及统计线损之间的关系，根据各节点负荷的输入计算最终的统计线损值，然后在输入接电负荷、统计线损以及理论线损的基础上分析线损的重要因素比及是否存在窃电情况[2]。

理论线损是指电力传输过程中损耗的电能，利用均方根电流法和损耗因素法计算。将已有潮流数据作为人工神经网络模型的输入，线损作为输出，具体的理论线损计算为：

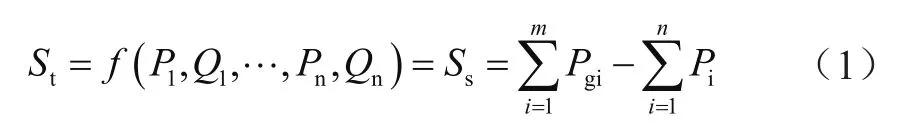
式中，St和Ss分别表示理论线损和统计线损；f表示神经网络训练所得线损计算函数；Pi和Qi分别表示第i个负载母线上的有功功率和无功功率；Pgi表示发电机发电功率。

2 样本训练及窃电位置分析

2.1 样本训练分析

人工神经网络模型的建立需要依靠大量可靠的训练数据，因此数据积累非常重要。在实际应用过程中，配电网相应位置设有可以采集数据的表计，样本训练可以利用仿真来获取数据。线损计算需要的数据主要是各个位置的有功负荷和无功负荷，实际应用中标记线损数据量相对较少，很难得到实时的线损数据，在此用IEEE14节点标准网络实施仿真模拟[3]。

以典型潮流分布为基础实施数据仿真，以获取相对完整的仿真数据。仿真形式设定小范围波动（±10%）负荷300组，大范围波动（±50%）负荷300组，满足每次切除1个负荷节点情况的负荷420组。在所有1 020组都完成输入后，利用典型潮流计算方式获取对应的潮流输出，得到对应的1 020组数据[4]。这些数据中，人工神经网络的有效输入量为22组，属于算例中配电网的11个PQ节点的有功值和无功值，将这些数据当成训练样本来实施模型的训练。

2.2 窃电位置分析

通过远抄电量采集模块将其与SQL Server 2000数据库相连，比较分析数据库中的理论线损计算相关数据与本系统计算所得的统计线损相关数据。在潮流模拟仿真时，选择3、4、9、10、14这几个典型节点为窃电节点，从上述数据中选定负荷波动在±20%范围内的3 000组潮流数据和线损值，同时设定没有出现窃电情况，不考虑表计故障等外部因素影响的情况下，理论线损值就是统计线损值。将3 000组数据分为5类进行窃电分析，表计值随着窃电的发生也会有所下降，但是因为实际用量没有发生改变，所以统计线路也没有产生变化。此种情况下能够获取3 000组负荷相应的理论线损及统计线损，并且将潮流情况与线损值当成输入，将窃电的产生和作为当成输出，建立窃电分析模型[5]。为保证训练的成果，除了获取训练样本外还要设置测试样本，如表1所示。

表1 测试样本设置情况

2.3 神经网络训练模型设置

神经网络参数调节是提升计算准确性和效率的核心，为有效提高训练效率，实施数据的归一化处理，控制数值在[-1,1]，归一化函数设定为：

式中，y表示归一后的数值；x表示原始值；ymax和ymin分别为1和-1。

确定好归一函数后要设定神经网络节点，可以采用双隐含层的方式进一步提升准确性，节点数分别设置为11、10。采取梯度下降算法设定训练函数，具体形式为：

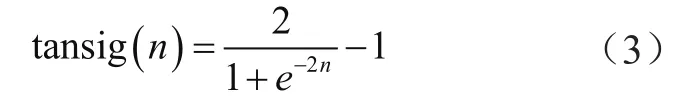
式中，n表示前一神经元传递输入值，范围控制在（-1,1）。将迭代次数设置为10 000，精度设置为0.01%，学习步长为0.1，考虑检验的有效性，在两次迭代偏差小于设定值或者偏差扩大时要自动停止迭代[6]。

3 算例的结果和具体分析

3.1 线损计算结果分析

对潮流模拟所得的1 020组结果，根据不同类别随机选择相应的测试样本，包括低负荷波动20组、高负荷波动20组以及满足切除情况28组。将其他样本当成训练样本实施模型训练，得到神经网络训练线损计算模型收敛结果如图2所示，理论线损和实际线损的误差如图3所示[7,8]。

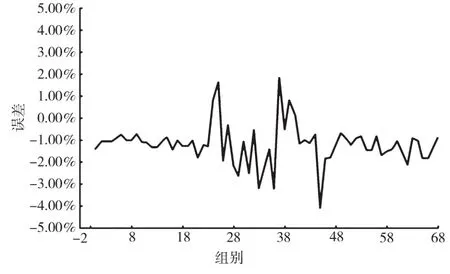
图2 神经网络训练线损计算模型收敛结果

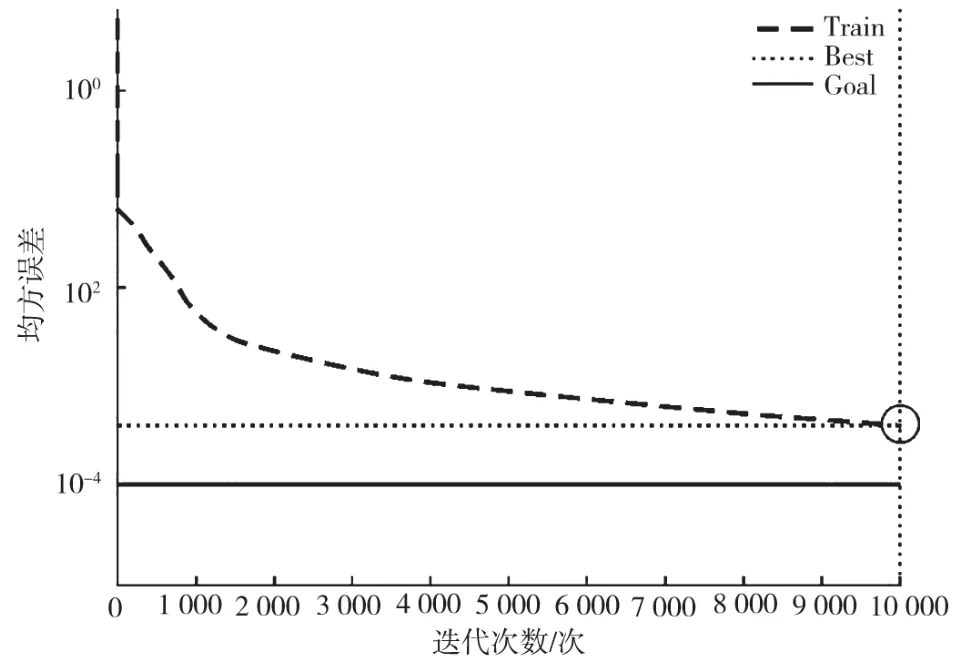
图3 理论线损和实际线损的误差

3.2 窃电位置分析

梯度下降算法下窃电位置分析的结果如表2所示，训练样本相同的情况下可以达到比较高的准确率。

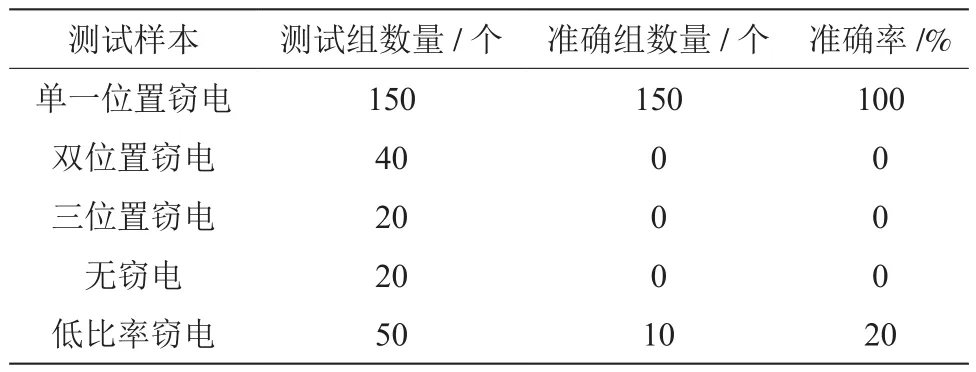
表2 窃电位置分析结果

随着窃电节点数量的上升，模型无法有效识别窃电量下降。神经网络模型对于泛化能力的要求较高，传统梯度下降学习算法无法满足，因此要对其进行优化。

列文伯格-马夸尔特法是目前普遍应用的非线性最小二乘算法，可获取最小化非线性数值解。其使用Keras库建立神经网络模型，设定KM神经网络的输入节点数为3，输出节点为1，隐藏节点数为10，使用Adam方法求解，隐藏层使用ReLU(x)=(0,x)为激活函数，通过修改参数来获取梯度下降法和高斯-牛顿算法的优点。列文伯格-马夸尔特法具有较快的收敛速度和较强的泛化性，但每次迭代需要消耗较长时间并且内存占比较大[9]。

相较于梯度下降算法，采用列文伯格-马夸尔特法能有效提升多窃电位置识别的准确性和模型泛化识别能力[10]。由于训练的样本相对单一，对不同的窃电比率缺少识别敏感度，因此在无窃电和低比率窃电的情况下还是很难识别窃电位置。为提升识别准确性，增加无窃电500组以及各节点5%窃电数据共3 000组后再次实施神经网络训练，发现增加训练样本后无窃电和低比率窃电识别效果较好[11]。