火箭发动机涡轮叶片疲劳寿命可靠性分析
2020-05-06姜金朋刘志超
姜金朋,刘志超,刘 筑,巩 帆,王 珏
(1.空间物理重点实验室,北京 100076; 2.中国运载火箭技术研究院 总体设计部,北京 100076)
0 引言
随着人类进出太空日益频繁,为了降低成本,运载火箭正在向重复使用方向发展[1-3],作为火箭主要部件的液体火箭发动机也对重复使用性能提出更高要求。涡轮泵是液体火箭发动机中失效概率最高的部件,涡轮叶片是限制发动机寿命的关键因素之一[4-6]。由于生产加工和使用过程中材料属性、结构尺寸以及工作载荷等的随机性,涡轮疲劳寿命通常存在较大的分散性,确定性寿命预估很难保证结构寿命的可靠度;而传统的安全系数方法,为了保守设计通常取较大的安全系数,容易造成使用寿命浪费。美国的发动机结构完整性大纲中指出,用概率设计裕度代替传统的安全系数或确定性裕度能更准确地表示构件响应的变化[7]。
早在20世纪80年代初,参数的分散性就受到关注,Haubert等[8]研究了高压涡轮叶片寿命对叶片几何、材料、导热等相关参数的敏感度。SSME研制过程中,专门进行了概率结构分析方法的研究,并基于有限元和概率分析方法编写了概率结构分析程序NESSUS,对典型部件(包括涡轮泵、主推力室等)进行概率结构分析[9-11]。Monte Carlo模拟、一阶矩/二阶矩可靠性方法、响应面法(RSM)和设计试验(DOE)等方法被用于高周疲劳可靠性分析、蠕变疲劳可靠性分析和基于应变的疲劳可靠性分析[12-14]。国内研究者对航空发动机涡轮盘和涡轮叶片开展了大量研究,胡殿印等[15]提出了低循环疲劳寿命的概率设计方法,马艳红等[16]针对航空发动机中叶片高周疲劳问题,提出叶片在气流激励下的高周疲劳概率寿命预估方法。
本文考虑结构几何参数、材料属性、工作载荷等变量的随机性,采用Monte Carlo模拟法与响应面法相结合的方法,对液体火箭发动机涡轮叶片进行概率疲劳寿命分析,确定了涡轮叶片疲劳寿命可靠度模型,并分析了变量分散度对疲劳寿命的影响。
1 计算模型及方法
由于Monte Carlo模拟法计算样本数量大,而疲劳寿命预估模型中的流场分析和结构分析计算量大、计算时间长,因此,采用响应面近似法建立涡轮叶片疲劳寿命的响应面模型,代替CFD和有限元计算进行Monte Carlo抽样模拟分析。该方法流程如图1所示。
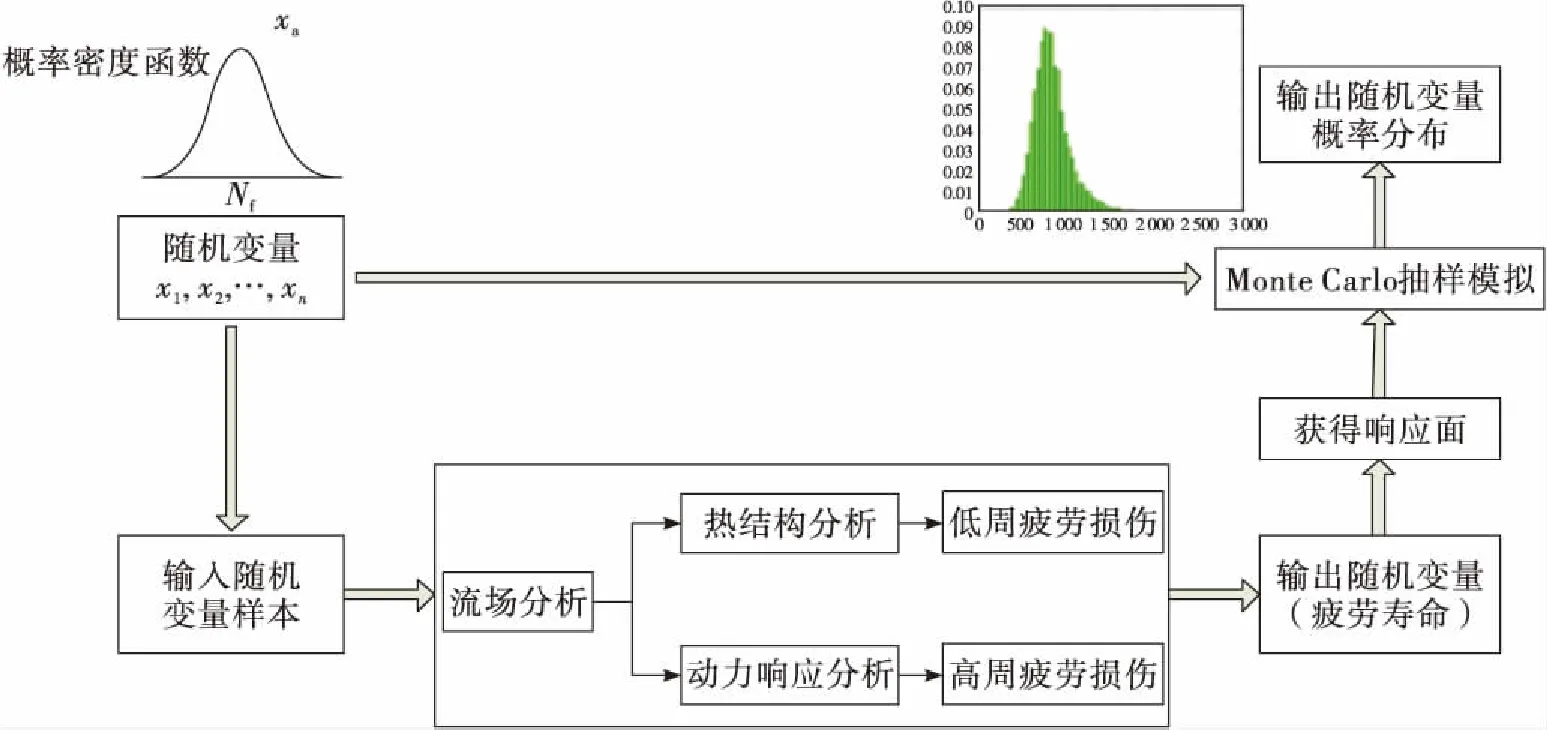
图1 疲劳寿命概率分析流程图Fig.1 Flow chart of probability analysis of fatigue life
1.1 计算模型
以某发动机涡轮叶片(图2)为研究对象,开展叶片热结构和动力响应分析。考虑到涡轮周向的循环对称性,取一个叶片进行仿真计算,为了合理施加约束和载荷,同时取部分叶冠和轮盘进行结构分析,计算模型如图3所示。对轮毂中心线上的节点施加径向约束,约束中心线下游端面中心轴半径范围内节点的轴向位移;对叶冠和轮毂周向面上的节点施加耦合约束,得到循环对称边界,约束轮盘突台周向面上节点的周向位移。热载荷和气动载荷施加到所有与燃气接触的面,包括叶冠表面、叶片表面及轮毂上表面,通过建立表面效应单元,将流场仿真得到的叶片对流换热系数、主流温度和气动压力插值到结构分析模型上。

图2 涡轮整体轮盘几何模型Fig.2 Geometric model of turbine blisk

图3 涡轮叶片结构分析模型Fig.3 FE model of turbine blade
1.2 随机因素分析
涡轮叶片相关的几何、材料、载荷参数众多,加上疲劳寿命预估中流场和结构分析计算量大,难以分析所有的参数,本文选取影响疲劳寿命的主要参数作为输入随机变量进行研究。
涡轮叶片的低周疲劳损伤取决于叶片的瞬态热结构响应,相关参数包括:几何参数、材料参数(包括热性能参数、力学性能参数等)及载荷参数(热载荷、离心载荷等)。Haubert[8]指出,导热相关参数对寿命的影响明显,而几何参数的影响小,因此,选取热膨胀系数作为随机变量。研究表明[17],材料参数中弹性模量和密度对低周疲劳寿命影响可观,选其作为随机变量。由于疲劳损伤与材料疲劳性能参数直接相关,选取材料疲劳强度系数σ′f、疲劳塑性系数ε′f、疲劳强度指数b、疲劳塑性指数c作为随机变量。叶片的热载荷主要由涡轮入口参数决定,因此,选取来流的入口总温、总压作为随机变量。涡轮转速作为离心载荷,选取为随机变量。
涡轮叶片的高周疲劳损伤取决于叶片在尾流激振力作用下的响应,而叶片响应由叶片的模态特征和激励特征决定[18]。影响模态特征的参数包括叶片结构尺寸、弹性模量、密度等,已选取弹性模量和密度作为随机变量。激励特征包括尾流激振力的频率、幅值等,在静叶数目一定的情况下,涡轮转速决定了激振力载荷的主要频率分量,选取转速作为随机变量。另外,研究表明,动静叶轴向距离对叶片上的气动力幅值有显著影响[19-20],考虑到装配时可能产生的误差和随机性,选取动静叶轴向距离作随机变量。

1.3 响应面模型
本文采用带交叉项的二次多项式对涡轮叶片疲劳寿命进行响应面拟合,参数变量对照表如表2所示,模拟的输出变量函数形式为
(1)
采用26组样本点进行响应面拟合,得到叶片疲劳寿命响应面拟合系数如表3所示,取10组样本点进行误差分析,多元确定系数R2为94%,大于90%,满足样本可信度标准。
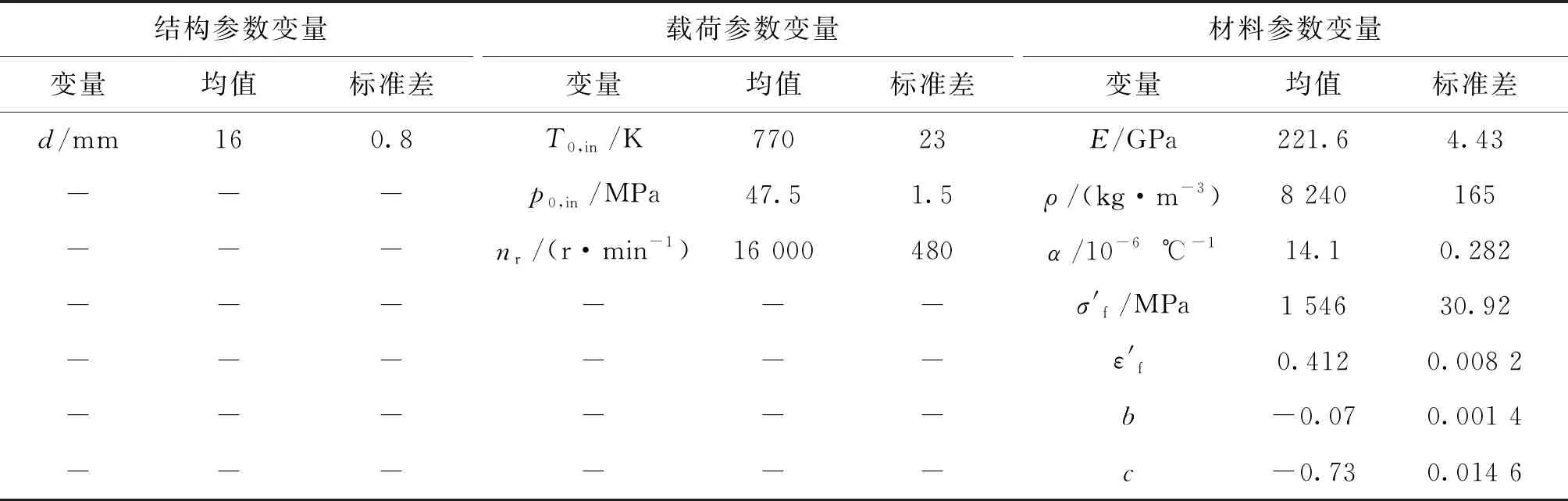
表1 随机变量及分布
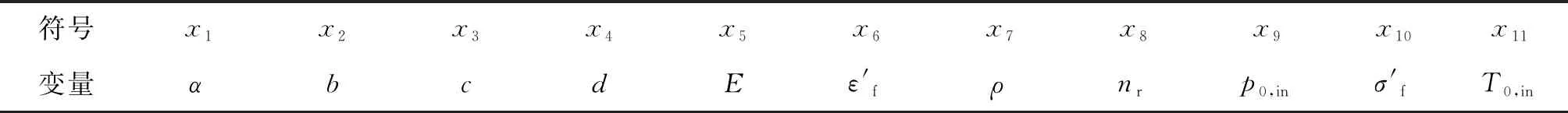
表2 变量对照表

表3 疲劳寿命响应面拟合系数
取100个样本点,采用拉丁超立方设计方法在叶片疲劳寿命响应面上进行DOE(Design of Experiments)分析,得到疲劳寿命对各随机变量的敏感度如图4所示。

图4 疲劳寿命对各随机变量的敏感度Fig.4 Sensitivity of fatigue life to random variables
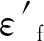
2 寿命可靠性分析
2.1 疲劳寿命概率分布
在疲劳寿命响应面上,对随机变量进行10 000次抽样模拟,得到的疲劳寿命频率分布如图5所示,可以看出,疲劳寿命呈明显的偏态分布。分别用威布尔(Weibull)、对数正态(Lognormal)、Logistic、Log-Logistic分布拟合疲劳寿命概率密度,其中,Log-Logistic分布函数与抽样模拟结果吻合最好。
Log-Logistic分布的概率密度函数
(2)
式中:α为尺度参数;η为尺度参数;β为形状参数。 累积概率分布
(3)
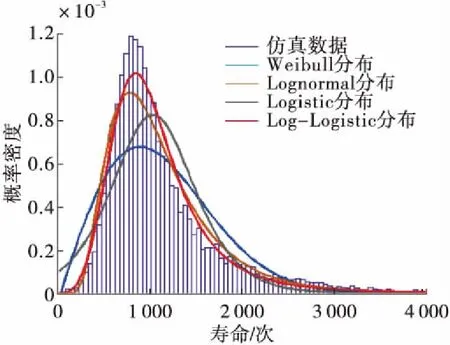
图5 疲劳寿命概率密度Fig.5 Probability density of fatigue life
图6给出了模拟试验和拟合的疲劳寿命累积概率分布曲线,累积概率在0~0.75范围内时,拟合结果与模拟试验结果基本一致。
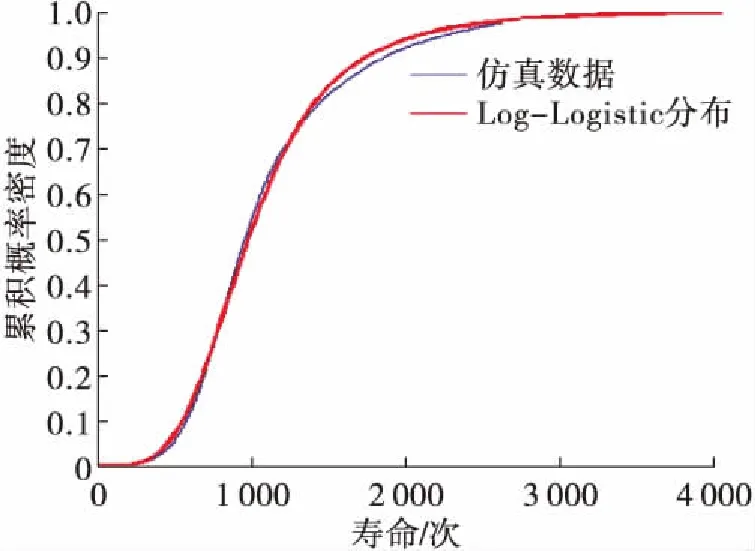
图6 疲劳寿命累积概率密度Fig.6 Cumulative probability density of fatigue life
2.2 疲劳寿命可靠性模型
对于某一寿命待评估的发动机涡轮,其疲劳寿命可靠度可定义为该涡轮在指定的工作条件下,寿命能够达到指定寿命的概率,即
R(Nd)=P(Nf≥Nd)
(4)
式中:Nd为指定的寿命指标;Nf为满足一定随机分布的涡轮疲劳寿命。
根据以上定义,叶片疲劳寿命可靠度
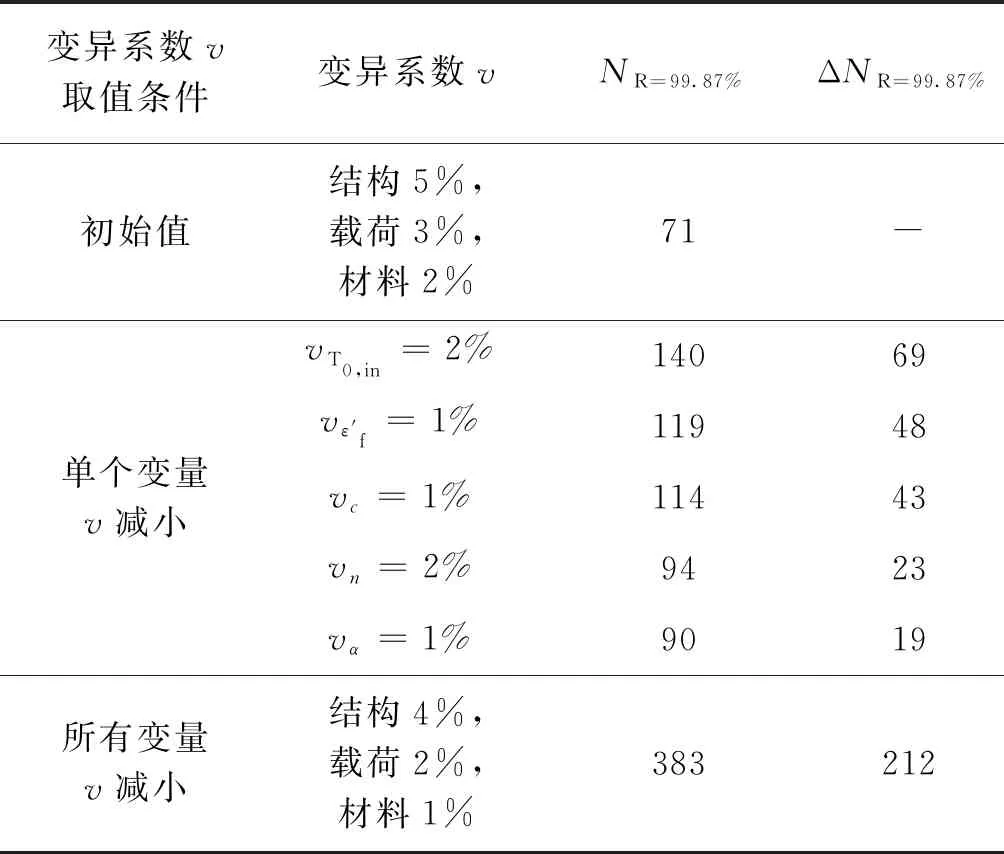
R(Nd)=1-P(Nf (5) 式中:P(Nf (6) 因此,发动机涡轮叶片疲劳寿命可靠度 (7) 寿命评估重点关注高可靠度区域,由图6可知,低累积失效概率区域内,拟合结果与模拟试验结果基本一致,因此,本文给出的疲劳寿命可靠度是合理可信的。图7给出了涡轮疲劳寿命可靠度与指定寿命的关系,保证可靠度达到99.87%的疲劳寿命最大为71次。 图7 疲劳寿命可靠度Fig.7 Reliability of fatigue life 随机变量的取值范围直接影响叶片疲劳寿命的分布,从而影响疲劳寿命可靠性,在实际使用过程中,可以通过控制加工、装配及工作过程中的调节精度等,控制随机变量的分散度。在上文分析基础上,通过控制随机变量的分散度(用变异系数v来反映),研究各随机变量分散度对疲劳寿命及可靠性的影响。 涡轮入口温度T0,in的变异系数分别为3%和2%时,涡轮叶片疲劳寿命的可靠度如图8所示,可以看出,当入口温度分散度低时,对于某一指定寿命(高可靠度区域),低分散度下的可靠度略高于高分散度下的可靠度,当变异系数为2%时,叶片安全寿命(保证可靠度达到99.87%的最大疲劳寿命)为140次。 图8 不同温度分散度的疲劳寿命可靠度 Fig.8 Reliability of fatigue life with differenttemperature dispersion 当各随机变量分散度均控制在较低水平,结构参数变量、载荷参数变量、材料参数变量的变异系数分别取为4%,2%,1%,涡轮叶片疲劳寿命可靠度如图9所示,可以看出,当各随机变量分散度低时,疲劳寿命分布更加集中,分散度显著降低,叶片安全寿命为383次。 图9 不同分散度的疲劳寿命可靠度 Fig.9 Reliability of fatigue life with differentvariable dispersion 表4中给出了不同随机变量分散度(包括单变量分散度变化及所有变量分散度同时变化)下的叶片安全寿命,结果表明,控制单变量分散度时,前文分析中对疲劳寿命影响较大的5个变量分散度减小时,安全寿命增大,且各变量分散度对叶片安全寿命影响大小的规律与变量敏感度一致,其中,入口温度变异系数减小0.01,叶片寿命增加约1倍,而同时控制所有变量分散度,使变异系数减小0.01时,叶片寿命增加约3倍。可以看出,控制变量分散度可以提高叶片安全寿命,对单变量而言,控制涡轮入口温度分散度效果最显著。 表4 不同分散度时叶片安全寿命 Tab.4 Blade life with different variable dispersion 变异系数v取值条件变异系数vNR=99.87%ΔNR=99.87%初始值结构5%,载荷3%,材料2%71-单个变量v减小vT0,in=2%14069vε'f=1%11948vc=1%11443vn=2%9423vα=1%9019所有变量v减小结构4%,载荷2%,材料1%383212 本文考虑涡轮叶片载荷、材料、几何等方面的不确定性,针对某火箭发动机涡轮,开展了叶片概率疲劳寿命分析及可靠性分析,建立叶片疲劳寿命可靠性模型,得到以下结论: 1)涡轮入口温度对叶片疲劳寿命影响最大;材料的低周疲劳性能参数ε′f,c对寿命影响较大;转速及热膨胀系数对寿命有一定影响;其余变量对寿命的影响小。 2)疲劳寿命呈偏态分布,与Log-Logistic分布拟合结果最接近。 3)控制单变量分散度时,各变量对叶片安全寿命影响大小的规律与变量敏感度一致,入口温度变异系数由0.03减小到0.02,叶片安全寿命增加约1倍;控制所有变量分散度,疲劳寿命分散度明显降低,各变量变异系数均减小0.01,叶片安全寿命增加近3倍。控制变量分散度是提高叶片安全寿命的有效途径,对单变量而言,控制涡轮入口温度分散度效果最显著。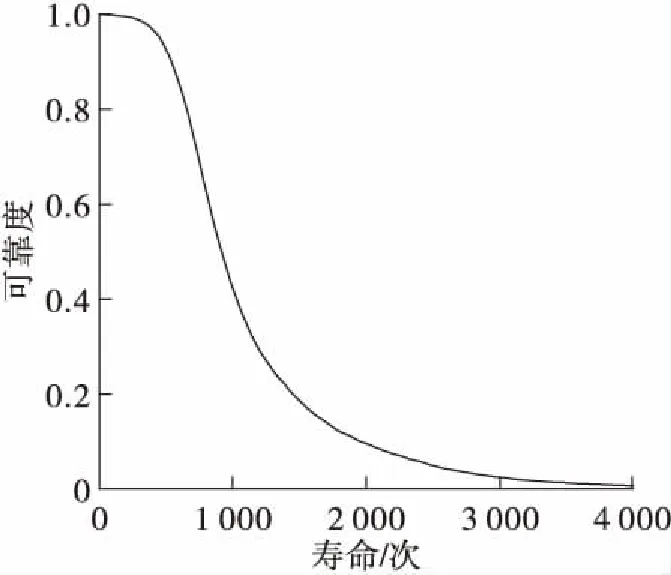
2.3 变量分散度对疲劳寿命的影响分析


3 结论
