基于应变量耦合的低成本Ti-Al-V-Fe合金本构关系

吴晓明,王 玉,高 斌,苏彦庆

(1.西安航天发动机有限公司,陕西 西安 710100;2.哈尔滨工业大学,黑龙江 哈尔滨 150001)

0 引言

钛及钛合金因其高强度、低密度、耐腐蚀等特点,广泛应用于航空航天、船舶等领域[1-6],在能源、汽车等民用领域,也有巨大的应用潜力,但是与钢铁、铝相比,过高价格成为其大规模应用瓶颈。廉价合金元素替代贵金属元素成为目前研究热点[7-10],如美国Timet公司开发的Timetal62s合金、西北有色金属研究院开发的Ti18Lc和Ti12Lc合金、美国华昌公司开发的ATI425合金以及哈工大苏彦庆课题组与云南钛业共同研发的低成本Ti-Al-V-Fe合金。

钛合金变形敏感性较高,工艺复杂,变形控制因素多,传统试错模式增加了重复试验量,提高了制造成本。材料流变应力模型通过数值理论模型计算分析加工过程应力场及温度场的变化规律,可预测组织演变规律及缺陷位置,有利于模具设计及改进方案制定,降低试验次数,加快研制进展,降低成本。

1 实验材料及方法

1.1 合金制备

按照设计成分以海绵钛、纯铝、纯钒、铁丝、二氧化钛为原材料进行配料,经过3次真空非自耗熔炼制备试样,以达到成分均匀。试样主要化学成分如表1所示。

表1 Ti-6Al-2.5V-1.5Fe-0.15O合金化学成分

Tab.1 Chemical composition of Ti-6Al-2.5V-1.5Fe-0.15O alloy单位：%

1.2 热模拟实验

实验设备为Gleeble-1 500 D,采用真空感应加热,主要参数：升温速率为10 ℃/s；相变点以下变形温度为875 ℃,900 ℃,950 ℃,相变点以上变形温度为1 000 ℃，1 050 ℃，1 100 ℃；应变速率为0.001 s-1,0.01 s-1,0.1 s-1,1 s-1；变形量为70%。试验结束后立即进行水淬。

1.3 试样尺寸

试样尺寸为φ6 mm×9 mm,在其两端加工凹槽储存高温润滑油,以减少摩擦对实验结果的影响。

2 实验结果与讨论

2.1 相变点

为了确定热变形温度设定范围,需要准确测定合金的相变点。金相法、差热分析法、计算法是目前常用的测定方法[11-12],本文以计算法为参考,差热分析法为主,确定了合金的相变温度。

2.1.1 计算法

计算法以各元素对相变的影响为依据,具体计算方法如下

T=885+∑(ab)

(1)

式中：a为相变点影响元素含量；b为相变点影响元素影响值。

表2为各元素对于合金相变点的影响值,将表1中的化学成分实测值代入式(1),可得相变点为995.9 ℃。

表2 各元素相变影响值

Tab.2 Effect of chemical composition onphase transition

元素类型名称含量/%影响值α相稳定元素AlNO0.0-2.0+14.5 ℃/1%2.0-7.0+23.0 ℃/1%0.0-0.5+5.5 ℃/0.01%0.0-1.0+2.0 ℃/0.01%β相稳定元素H0.0-0.5-5.5 ℃/1%Fe0.0-15.0-16.5 ℃/1%V0.0-3.8-13.9 ℃/1%中性元素Zr--2.0 ℃/1%Sn--1.0 ℃/1%

2.1.2 差热分析法

差热分析法是合金相变点测定常用方法,其通过分析被测试样与标准试样在加热过程中的失重速度的差值,获得热流与温度曲线[13-14]。图1为采用SDT-Q600热重分析仪测得合金的DSC曲线。(α+β)→β相转变属于吸热反应,随着温度升高,α相不断转化为β相,这是一个持续转变过程。第一个吸热峰温度区间为850～925 ℃,与计算法差异较大,其主要与钛合金与坩埚、氮气发生反应有关。第二个吸热峰(975～1 000 ℃)因相变吸热而产生。一般将DSC曲线对温度一阶导数的峰值定义为钛合金的β相转变点[13],DSC曲线一阶导数峰值为991 ℃,与计算法得出的结果接近,可确定合金的相变点为991 ℃。

图1 差热分析结果Fig.1 DSC results

2.2 真实应力应变分析

图2为不同变形温度、应变速率的合金真实应力应变曲线,由图可以看出：合金变形分为非稳态、稳态两个阶段[15]。变形初期,即ε<0.5εP(峰值应力),流变应力急剧增加,合金呈现非稳态变形特征。当0.5εP<ε<εP,随着变形程度增加,位错数量急剧增加,组织转变的驱动能量显著增加,有利于动态再结晶及动态回复软化的进行,流动应力增长渐缓。当ε>εP,合金软化占据主导地位,流变应力出现明显降低。当二者达到平衡时,则达到稳态阶段。

图2 不同变形温度、应变速率的Ti-6AI-2.5V-1.5Fe-0.15O合金真实应力应变曲线 Fig.2 True stress-strain curves of Ti-6Al-2.5V-1.5Fe-0.15Oalloy under different deformation temperatures andstrain rates

流变应力与变形温度、应变速率呈现以下特征：流变应力与变形温度成反比,与应变速率成正比。随着变形温度的提高,再结晶及动态回复驱动能增加,有利于晶粒形核、长大；减小了晶粒以及晶粒间的变形程度,降低了变形阻力,流变应力减小。随着应变速率增加,位错增殖加剧,变形抗力增加,动态再结晶、动态回复时间缩短,软化效果变差，流变应力提高[16]。

两相区变形(相变点以下变形)以动态再结晶为主,这种方式在达到峰值应力后迅速降低;单相区变形(相变点以上变形)以动态回复为主,这种方式并未出现流变应力骤降,而是以一种相对较低速度缓慢降低。

2.3 建立本构方程

材料的本构方程是利用数学模型描述流变应力与应变速率和变形温度等热变形工艺参数的函数关系，本构方程为

(2)

当应力水平较高时,即σ>1.2/α,应变速率使用指数型方程描述，表达式为

(3)

当应力水平较低时,σ<0.8/α,应变速率使用幂函数型方程描述，表达式为

(4)

Sellars和Mctegart等人[17]综合式(3)和式(4),提出了含有热激活能Q的双曲正弦函数Arrhennius本构方程

(5)

式中：n1为应力指数；A为材料常数；R为阿伏伽德罗常数；Q为热激活能。

Zener和Hollomon等人[18]提出了温度补偿速度Z参数,并通过试验验证Z参数的影响,该模型考虑变形条件的影响,拓展原有方程的使用范围,成为目前应用最为广泛的流变应力模型，表达式为

(6)

为了表征应变速率和温度的影响,可将式(5)和式(6)结合，导出

(7)

对于材料常数A、热激活能Q、应力指数n可通过以下步骤完成。

当变形温度一定时,对式(3)和式(4)两边取自然对数，可得

lnε=lnA+nlnσ

(8)

lnε=lnA+βσ

(9)

对式(5)求导、变形,即可求解热激活能

(10)

对式(6)取自然对数,可得

lnZ=lnA+nsinh(ασ)

(11)

以应变量为0.45为例,流变应力如表3所示,计算求解过程如图3所示,将复杂应力应变问题转化为Z参数模型中的A，α，n及Q常数的求解。

图3 本构方程求解流程Fig.3 Solving precedure of constitutive equation

图4为不同应变速率下流变应力σ与T/1 000之间的关系,两相区与单相区呈现明显不同的曲线特征,因此需要分相区分析。

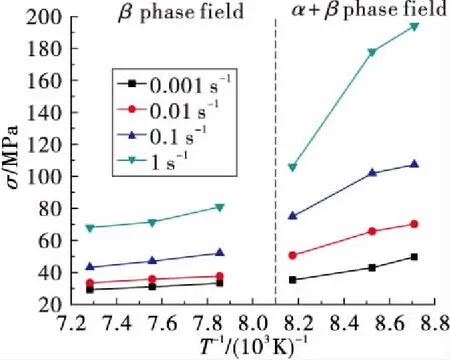
图4 稳态应力与变形温度关系Fig.4 Relationship between steady state stress anddeformation temperature

根据式(8)和式(9),绘制相应的lnε，lnσ，lnε和σ,最小二乘法线性回归得图5(a)和图5(b)。两相区：n=5.435 61，β=0.062 783,α=0.0112 84;单相区：n=7.550 78，β=0.155 09,α=0.020 511,相关系数R大于0.95,表明拟合良好。

将α代入sinh(ασ),绘制lnε-ln sinh(ασ)以及ln sinh(ασ)-T-1散点图,线性拟合结果如图5(c)和图5(d)所示,两相区：n1=4.040 277，n2=1.105 025，Q=371 187.4 kJ/mol;单相区：n1=5.976 323，n2=0.419 398，Q=202 110.3kJ/mol。

利用式(11)计算Z常数,同时绘制lnZ与ln sinh(ασ)曲线,根据其斜率及与纵坐标交接值可得材料常数,两相区n=3.791 93,lnA=33.972 93;单相区n=5.711 09,lnA=18.371 56。其拟合结果如图5(e)和图5(f)所示,两相区的相关系数为0.974,而单相区相关系数为0.986,表明双曲正弦模型可用于描述合金高温变形行为。

表3 应变量为0.45时不同应变条件下的流变应力

图5 应力与应变速率、温度之间拟合关系Fig.5 Fitting relationships between stress and temperature, stress and strain

通过以上计算可求得应变量为0.45的应力-应变关系方程

(12)

(13)

2.4 基于应变量耦合的本构模型分析

双曲本构方程中并未包含应变量的影响,使用范围较窄。本文以热压缩模拟实验和本构方程建立步骤为依据,求得不同应变下(ε=0.05～0.55,间隔为0.05)的材料常数,建立了应变量耦合的本构模型。

两相区模型

α=0.016 09+0.004 88ε+0.008 99ε2+0.021 75ε3-0.050 9ε4

n=5.85+7.17ε-22.51ε2+7.21ε3+12.811ε4

Q=182 162+417 126ε-34 372ε2-2.669 2×106ε3+2.965 31×106ε4

(14)

lnA=13.19+33.85+40.28ε2-364.25ε3+374ε4

单相区模型

α=0.015 93+0.010 66ε-0.097ε2+0.040 2ε3-0.054 5ε4

n=5.99+9.94ε-43.165ε2+51.65ε3-15.72ε4

Q=2 810 768.6-593 896.2ε-2.59×106ε2-5.50×106ε3+3.07×106ε4

(15)

lnA=21.24-49.63ε+194.63ε2-

353.88ε3+192.05ε4

Pilehva F，Char R[19-20]采用四次多项式成功拟合多种合金的真实应力-应变关系。本文借鉴其研究方法,采用四次多项式线性回归方法,获得材料常数、应变量关系,表4、表5为试验结果,图6为各材料常数与应变关系,其中各参数拟合误差系数R为0.97～0.99。将上述材料常数计算结果代入式(7),即可得到应力应变关系,该方程的耦合系数为0.98,表明此方程预测效果良好。

表4 β相区材料常数回归结果

表5 α+β相区材料常数回归结果

图6 材料常数与应变关系Fig.6 Relationship between material constants and strain

2.5 热激活能

热激活能显著影响变形速度,从而影响合金软化机制。材料热激活能与自身激活能数值相近时,动态回复占据主导地位,当变形激活能远大于自扩散激活能时,以动态再结晶为主[21]。

上述结果显示,两相区、单相区热激活能分别为398 kJ/mol,211 kJ/mol,而纯钛热激活能169 kJ/mol,结合真实应力应变曲线特征,可推断两相区软化机制为动态再结晶,而单相区为动态回复。因此两相区变形为该合金最佳工艺窗口。

3 结论

1)流变应力与变形温度呈反比,与应变速率呈正比,合金为典型负温度、正应变敏感材料。

2)基于热压缩试验数据,计算材料的热激活能,通过热激活能数据,判别不同相区的软化机制,两相区软化机制为动态再结晶,单相区为动态回复。

3)基于实验数据,通过理论计算建立了基于应变耦合的α+β两相区及单相区Arrhenius本构方程,两相区变形为最佳变形工艺窗口。