例说用直线参数方程中参数的几何意义解题

叶正昆

(云南省曲靖市地区陆良县第八中学,655600)

参数t的系数满足平方和等于1,这是直线标准参数方程的一个重要特征，此时若直线与曲线f(x,y)=0相交于A、B两点,且A、B两点对应的参数值分别为t1、t2,则|AB|=|t1-t2|.

用参数的几何意义解决有关距离问题较方便,能简化圆锥曲线中复杂的运算.多数学生在解题时没有注意合理运用参数的几何意义,导致解题出错.本文举例示范,请同学们进行对比,以避免继续出错.

例1 已知过点M(-1,2)且斜率为1的直线l与抛物线y=x2交于A、B两点,分别求|MA||MB|与|AB|的值.

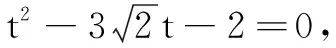
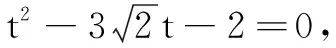
评注由解法1、解法2可见,利用参数的几何意义解题,对概念与结论把握越准确、深刻,则求解过程越简单、方便.

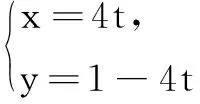
(1)求直线l的普通方程与圆C的直角坐标方程;

(2)设圆C与直线l交于A、B两点,求弦长|AB|的值.

解(1)直线l:x+y=1,圆C:x2+y2-2x-2y=0.(过程略)

(2)解法1利用参数方程一般形式

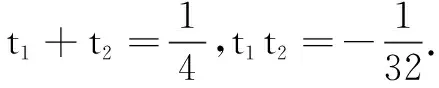
由42+(-4)2≠1,可知参数方程不是标准形式,所以

解法2利用参数方程的标准形式

|AB|=|t′1-t′2|