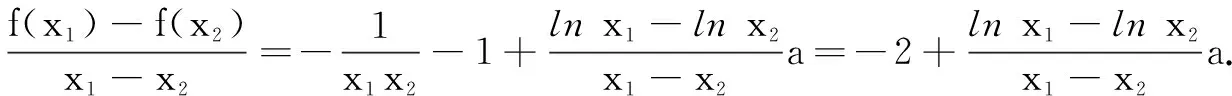探秘题根在求解导数压轴题中的作用

张国治 耿梁燕

(新疆生产建设兵团第二中学，830002)

著名数学家陈景润先生在谈起数学解题时,曾说过“题有千变,贵在有根”.以题根方式展开教学,旨在抓住解题思维入口,通过题根的变式拓展探求不同的解法,帮助学生理解问题内涵,总结归纳解题.本文以一道竞赛题为例,探源溯流,给出一类竞赛题、高考题命题的题根,探索一种高效学习数学的方法,敬请同行指正.[1]

题根(2017年全国高中数学联赛湖南省预赛题)[2]已知a、b>0且a≠b.

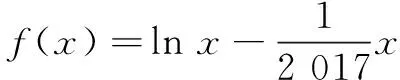
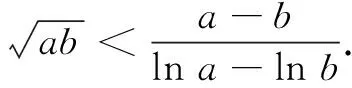
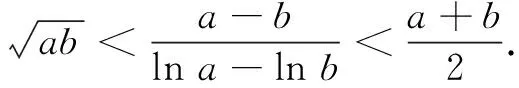
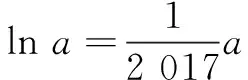
评注第(1)问为对数平均不等式，在近几年的竞赛、高考中应用非常广泛，可简化问题解答过程，开辟了不等式证明的新路.下面举例说明该题根在竞赛、高考题中的应用，帮助大家进一步谙熟此类问题的命题过程.

(1)若m=-2时,求f(x)的所有零点;

(2)若f(x)有两个极值点x1、x2,且x1e2.

解(1)略.

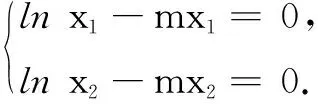
于是lnx1x2=lnx1+lnx2=m(x1+x2)>2,得x1x2>e2.

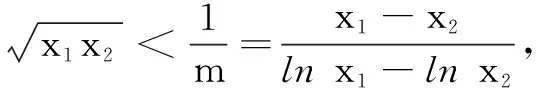
(1)若f(x)在(2,f(2))处的切线与直线x-y=0平行,求实数n的值;

(2)试讨论f(x)在[1,+∞)上的最大值;

(3)若n=1时,f(x)恰有两个零点x1、x2(02.

解(1)、(2)略.

(1)讨论f(x)的单调区间；

(2)若f(x)有两个极值点x1、x2,记过点A(x1,f(x1)),B(x2,f(x2))的直线斜率为k.问:是否存在a,使得k=2-a?若存在,求出a的值；若不存在,请说明理由.

例4(2018年全国高中数学联赛福建省预赛题)[3]已知f(x)=ex-mx.

(1)当x>0时,不等式(x-2)f(x)+mx2+2>0恒成立,求实数m的取值范围;

(2)若x1、x2是f(x)的两个零点,证明:x1+x2>2.

分析竞赛组提供的解答是利用第(1)问的结论证明第(2)问,思路并不自然.若联想到对数均值不等式，便有如下别具一格的解答，且第(2)问的证明不依赖与第(1)问.

解(1)略.

(2)证法1f′(x)=ex-m,若m≤0,则f′(x)>0,f(x)在(-∞,+∞)单调增,至多有一个零点，不合题意.若m>0,易见f(x)在(-∞,lnm)单调减,在(lnm,+∞)单调增,故f(x)min=f(lnm)=m(1-lnm).又x→-∞时,f(x)→+∞；x→+∞时,f(x)→+∞,故当f(lnm)=m(1-lnm)<0，即m>e时，f(x)有两个不同的零点x1、x2.不妨设x10,f(lnm)<0,结合零点的存在性定理知0

评注本题中巧妙的换元,使得问题迅速获解,但关键是需要明确到函数存在两个零点的条件.本文所提供的两种解法均不同于标准解答,且解法都优于标准解答，同时还可得到如下推广：

推论2若x1、x2是f(x)=ex-mx(m>e)的两个零点,则2

变式(2016年全国高考题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围;

(2)设x1、x2是f(x)的两个零点,证明:x1+x2<2.

由平均不等式不难获得问题(2)的证明，限于篇幅，这里不再赘述.请读者自行验证.

例5(2018年全国高考题)设函数

(1)讨论f(x)的单调性;

(2)若f(x)有两个极值点x1、x2,证明:

解(1)略.

(2)由(1)知,f(x)存在极值点当且仅当a>2.由于f(x)有两个极值点x1、x2满足x2-ax+1=0,所以x1x2=1,x1+x2=a.

总之,研究“题根”对教学、命题和解题都有深远的意义,变幻多端的数学题目犹如葱郁繁密的树叶．看似难以捉摸,实则息息相关,故而在研究问题时应拨开层层枝叶,寻其根源.“题根”的这种由基础到综合、由简单到复杂的教学方式既夯实了基础,符合“回归题根”的学习理念,也满足了不同学生的认知需求,为学生的个性化发展提供了滋养的土壤.[1]