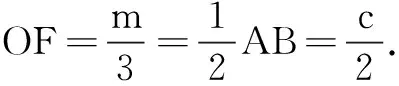例谈三角函数最值综合题的求解策略

孙莉娜

(江苏省扬州大学数学科学学院统计1801班，225002)

如同江苏高考填空题2010年第13题、2016年第14题,与三角函数有关的最值综合问题是近年来数学高考考查的难点和热点.解决此类问题能综合考查学生运用三角恒等变形、正余弦定理、基本不等式等知识解决最值问题的能力,综合性较高.此类问题备受师生关注,在各地模拟试题中也是层出不穷,属于学生感觉比较头疼的问题.本文以2019年一道模拟题为例,浅谈三角函数最值综合问题的求解策略,供大家参考.

一、求解策略及解法分析

解决此类问题,主要策略是将所求的量转化为关于单一变量的函数或双变量的表达式,最终用不等式等方法求最值.

策略1利用三角恒等变换进行消元

解法1由sin2B=2sin2C-2sin2A=(1-cos 2C)-(1-cos 2A)=cos 2A-cos 2C=cos[(A+C)+(A-C)]-cos[(A+C)-(A

-C)]=-2sin(A+C)sin(A-C)=-2sinBsin(A-C),故sinB=-2sin(A-C),即sin(A+C)=-2sin(A-C),展开整理得cosAsinC=3sinAcosC,可得tanC=3tanA.

策略2利用角化边进行消元

解法2由条件和正弦定理,可得2a2+b2=2c2.

策略3利用三角函数定义及基本几何图形进行消元

解法3如图1,设AC边上的高BD=h,AD=x,CD=y.由条件和正弦定理,得2a2+b2=2c2,所以2(h2+y2)+(x+y)2=2(x2+h2),即x2-2xy-3y2=0,可得x=3y.

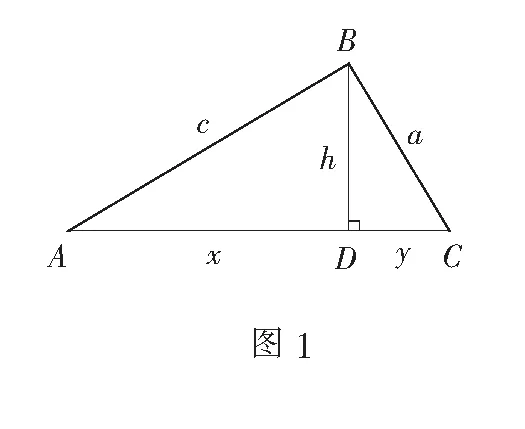
评注本解法关键是利用直角三角形中锐角函数的定义,通过构造直角三角形和利用约束条件,将正切函数解析式表示为关于h、y的二元表达式,再运用基本不等式使问题获解.

二、拓展变式

解(三角恒等变换法)

解(基本几何图形法)

如图2,作CD⊥AB于点D.设CD=h,AD=x,BD=y,则

①

2S=(x+y)h.

②

解(基本几何图形法)