基于SVD/小波的MEMS陀螺误差分析及降噪处理

杨菊花，张琳婧，陈光武，程鉴皓，刘 昊

(1.兰州交通大学 交通运输学院，兰州 730070；2.兰州交通大学 自动控制研究所 兰州 730070；3.甘肃省高原交通信息工程及控制重点实验室，兰州 730070)

0 引 言

微机电系统(micro electro mechanical system，MEMS)系列传感器因其低廉的成本和较高的使用性价比在惯性导航系统(简称惯导)中应用广泛，但其劣势是精度低，噪声高，特别是MEMS系列的陀螺仪。MEMS陀螺仪输出信号为典型的非平稳序列，其降噪性能的好坏对保证惯导精度起着重要的作用。为了提高MEMS陀螺的测量精度，常用的有时间序列分析和实时滤波方法。文献[1]提出一种基于遗忘因子递推最小二乘估计的时变自回归滑动平均模型补偿方法；文献[2]在基于噪声未知但分布有界的条件上引入一种具有递推特性的定界椭球自适应约束最小二乘法；文献[3]提出一种基于支持向量回归机的预测补偿算法。文献[4-5]使用了实时滤波技术，具体有卡尔曼滤波与小波变换，单纯使用滤波技术总是有很多假定条件，而非平稳序列明显不包括在假定条件里。依据文献[6]，陀螺噪声功率谱密度值在低频部分最显著，若选择低阶滤波对低频噪声无能为力，若选择高阶滤波则引起相位延迟。既然不可以把陀螺随机漂移视作可长期预测的随时间而变的平稳序列，也不可将它限定在频域上的某一端，那么，文献[2]中噪声未知但有界的思想可以借鉴，从滤波的技术层面来考虑输出时间序列的具体需求，摒弃建模的环节，正视信号的弱非线性，在时域与频域中并行降噪，由此提出一种基于SVD/小波的MEMS陀螺信号降噪处理方法。

1 MEMS陀螺的误差分析

实际使用中由于复杂多变的环境，根据MEMS陀螺解算的位置、姿态误差会不断累加，依据文献[7]，确定性误差和随机性误差是MEMS陀螺噪声的主要来源，而补偿误差的方式有3种选择：①设计电路或硬件结构，实行硬件补偿；②设计相关试验估计相关系数，实行软件补偿；③进行滤波矫正。前2种误差补偿的方式针对确定性误差，由于确定性误差中安装误差与比例因子误差为主要来源，而这2种误差可由转台的校准测试补偿，但因为这种补偿方式涉及不同转台的型号、性能和工作方式，所以先不考虑。第3种误差补偿方式针对随机性误差，这是目前研究的主要内容。

MEMS陀螺属于惯性器件，随机误差包括静态条件下测试的随机误差、确定性误差经过补偿后遗留下来的误差和实际使用环境中运载体线运动和角运动、温度、磁场、压力等任意组合激励出来的其余误差[8-10]，描述MEMS陀螺器件精度性最常用的指标是随机漂移稳定性。MEMS陀螺随机漂移是一个存在线性趋势项而缓慢变化的过程，在尺幅分解中，信号的低频部分随着层次的增加其含有的高频信息会随之减少，每增加一个分解层次，就会有更高频率的信息被去除，所剩下的就是信号的发展趋势，即表明陀螺输出信号是以低频为主的非平稳信号。

陀螺随机漂移作为一种非平稳序列，在整个时间和频率谱上是非均匀的，虽然貌似无规律可循，但此种序列在多个时间尺度上是存在自相似性的[11]，即拥有短期可预测的特性。小波变换降噪效果良好，但对微弱信号的去噪效果较差，存在诸如频率重叠、阈值不稳定以及分解和重构算法错误等问题，在信号分量和噪声分量的频带混叠比较严重时，小波降噪就有较大的局限[12]。微弱信号检测是在噪声下对微弱信号快速、准确、高灵敏度的采集和处理，奇异值矢量能显示矩阵的时频信息，现有小波结合奇异值的做法大多用在图像纹理分类与信号消噪上，有音频[13]的处理，加速度计[14]的消噪，对心电信号[15]的滤波等。

2 MEMS陀螺的降噪处理

小波降噪是根据信号和噪声的小波系数在不同尺度上具有不同性质的机理，在小波域内对含噪信号的小波系数进行处理，由于小波窗口面积大小不变而形状可变，因此，它在低频带中具有相对较高的频率分辨率和较低的时间分辨率。消噪过程如下。

1)选择合适的小波分解层次，对实际信号进行小波分解；

2)对小波分解后的高频系数进行处理；

3)重构信号，得降噪后的真实信号。

该处理有3点优势：①低熵性。小波系数的稀疏分布，使变换后的熵降低；②多分辨性。采用多分辨率的方法，能够非常好地刻画信号的非平稳性特征，比如断点、边缘、缝隙等；③选择基底的灵活。小波变换可灵活选择不同的小波基，降噪主要有小波包和阈值降噪法，相比较，阈值去噪使用方便，计算简单，效果良好，成为广泛使用的降噪方式。

2.1 小波框架

小波框架可以看作由一个母函数进行平移和膨胀作用后得到的一系列函数{φi,k}i∈I，设Sn为膨胀算子，Nn为平移算子，则φi,k=SnNnφ0,k。构造出来的小波框架φ需要尽可能地产生多的接近于零的系数(f,φi,k)逼近选定信号，φ有2个特点：①系数冗余；②系数必须无穷小。为了更好地描述信号的局部特性，希望φ具有短支撑性和足够的消失矩，短支撑性对应高的时间分辨率，高消失矩则对应构造小波基的无穷小性质。

对微弱信号的去除，其关键一步选取分解层数就不可如传统般地依据大量实验确定，不仅适应性差、计算量大，且降噪后信号大多数处于过度扼杀和过度保留的结果。基于此，设计了一种自适应选取分解层数的方式，分解层数代表滤波的反复性，这种反复性的分寸则由高频小波系数是否满足白化噪声来把握。

2.2 小波阈值

小波阈值降噪流程如图1，特别选择变换函数[16]g(x)对分解后小波系数进行细节放大，表示为

(1)

将系数谱中间混淆区域的差别放大，两端不易混淆的区域缩小，以便识别噪声，最后依据阈值选择分量进行重构。

所谓阈值去噪，主要工作就是对系数进行选定规则下的一个萎缩，无论是传统的阈值还是后续发展的模糊阈值，区别只在于选定规则的不同，实质依旧是萎缩系数。选取阈值表达[17]为

(2)

(2)式中：j为分解尺度；σ为噪声水平；γ为阈值常数；n为采样个数；a，b，c为调节因子。

2.3 SVD/小波

奇异值分解(singular value decomposition，SVD)作为一种信号分析的有效工具，特别针对非线性、非平稳的信号，可以将数据主导特征用少数分解系数集中体现出来，第1个优势，数量少；第2个优势，稳定。在具体应用中经过正交变换将原矩阵化为一个对角元素为奇异值的对角矩阵，由于SVD的稳定性和不变性[18]，序列通过SVD可分成2个不同的部分，一部分代表信号能量；另一部分代表噪声能量。奇异值在低于选定阈值时与噪声子空间相关，噪声存在于整个时间上且相互无关，所对应的奇异值小。信号的主要分量与大奇异值相对应，数值越大，坐标值在对应坐标轴上的离散程度越大，对应的能量和所占比重也越大，该坐标值反映的特征信息也越重要，基于此可以忽略较小奇异值所对应的坐标值。

SVD/小波算法的本质就是精细化分块后根据奇异值蕴含的权重信息得以构建小波系数谱的重分配规则。对于一维测量信号，可生成二维Hankel矩阵来使用SVD。首先为克服固定小波分解层数对降噪效果的限制，设计自适应算法确定小波最优分解层数N，选择依据为分解后的高频系数是否满足白化检验，满足则确定最优分解层数N；然后对信号进行N层分解，得小波系数向量W；接着引入SVD算法，处理W生成Hankel矩阵Z，Hankel矩阵Z经过SVD可得到一系列子矩阵的叠加，即得到时频矢量ui和vi，矩阵包含的时频信息也会被分解到由ui和vi构成的时频平面中；最后选取子空间提取小波系数进行重分配，通过阈值(1)式重构干净信号。经由SVD分解，每个子空间中的时频信息都通过ui和vi来表达，所以包含周期冲击、微弱分量的信号必然反映在子空间中的时间矢量和频率矢量上。流程图如图2。

3 试 验

针对陀螺降噪的算法验证，设计试验对比陀螺降噪前后的信号输出，分为静、动态2块内容。试验环境中使用的双轴电动转台如图3，技术参数如表1，图3中：标1处为主轴；标2处为俯仰轴；标3处为该系统配备的MEMS器件的AHRS航姿参考系统。该款AHRS航姿参考系统由三轴MEMS陀螺、三轴MEMS加表、三轴磁强计构成，是一款完整的9自由度全姿态测量传感器的组合装置，可实现三维空间任意位置和角度的姿态测量。

静态试验选取三轴转台内置AHRS航姿参考系统的MEMS陀螺输出的角速率进行分析，其输出频率100 Hz，采集时长180 s，外部输入量为零值，恒温条件，此时陀螺的期望输出值为零值，但实际值是在零值的上下范围内波动的，如图4。由于转台的振动和周围环境的干扰，实测时陀螺输出会存在一些在短时刻内大幅度跳跃的明显异常值，如图4中蓝色圆点所示，所以在采集实际输出值后需要对数据进行预处理，剔除掉不正常的跳跃值，预处理后信号信噪比为8.633 4。

表1 双轴转台的技术参数

选择dB3小波基对转台陀螺的零位噪声进行特征分析，如图5，由于小波每次分解都保留高通部分的滤波结果，所以信号的高频系数幅值随着分解层次的增加逐渐地增大，图5中的cd1，cd2，cd3分别为第1，2，3层小波分解后的高频系数，在这里已经体现了信号的细节特征。

MEMS惯性传感器的兴起和它性能的不断提高，已经是新一代INS的重要部件，并能满足车载导航系统低成本和微型化的需要。惯性导航的优势是高更新率，三维空间位置和速度以及姿态和航向信息的输出，根据这些信息就可以推导出载体的姿态，速度和位置。陀螺仪的输出是影响惯导平台解算的姿态精度的关键信息源。上述试验终究只是在一种平稳的试验环境里，无法检测该算法在动态环境中的性能，所以接着设计了动态试验。

动态试验使用双轴电动转台，MEMS的AHRS航姿参考系统是固定在转台主轴上的，连接电源将主轴置水平位后预热20 min，设定主轴和俯仰轴为10 °/s的恒定速率，其中，设主轴顺时针方向转动、俯仰轴逆时针方向转动，数据处理以陀螺仪的X轴输出信号为例，采集时长5 min，经采样与该文算法降噪处理后数据绘制如图6。

从统计学角度分析算法性能需要使用重构信号偏离原始信号的误差来衡量信号质量，常用的指标有均方根误差(root mean square error,RMSE)、信噪比(signal noise ratio,SNR)。动态验证比起静态较为复杂，所以采集了5组数据，分别是主轴和俯仰轴的恒定速率为10，15，20，25，30 °/s时的陀螺动态输出(转台速率转动为0～50 °/s)，并求出了5组数据降噪前后的信噪比与均方误差，如表2。选取传统小波阈值软阈值法与该文算法进行对比，小波阈值并没办法准确分解出小信号分量，即使信号会经过阈值化后重构，也依旧受到较多噪声干扰。频率谱图是在频率的角度上对算法的性能进行的分析，在统计意义下描述随机信号，就需要估计它的功率谱密度。功率谱的主要特点在于描述时间序列的频谱特性，是一种分析数据及表示数据特性的方法。该文对比了转台在10 °/s的速率下运动时陀螺降噪前后的信号，如图7，表明SVD/小波降噪方法能克服细节信号中噪声的干扰，降噪后的信号功率集中分布在低频段，信号优化效果良好。2种性能分析方法的数据对比，都验证了动态试验中该文算法的可行性。

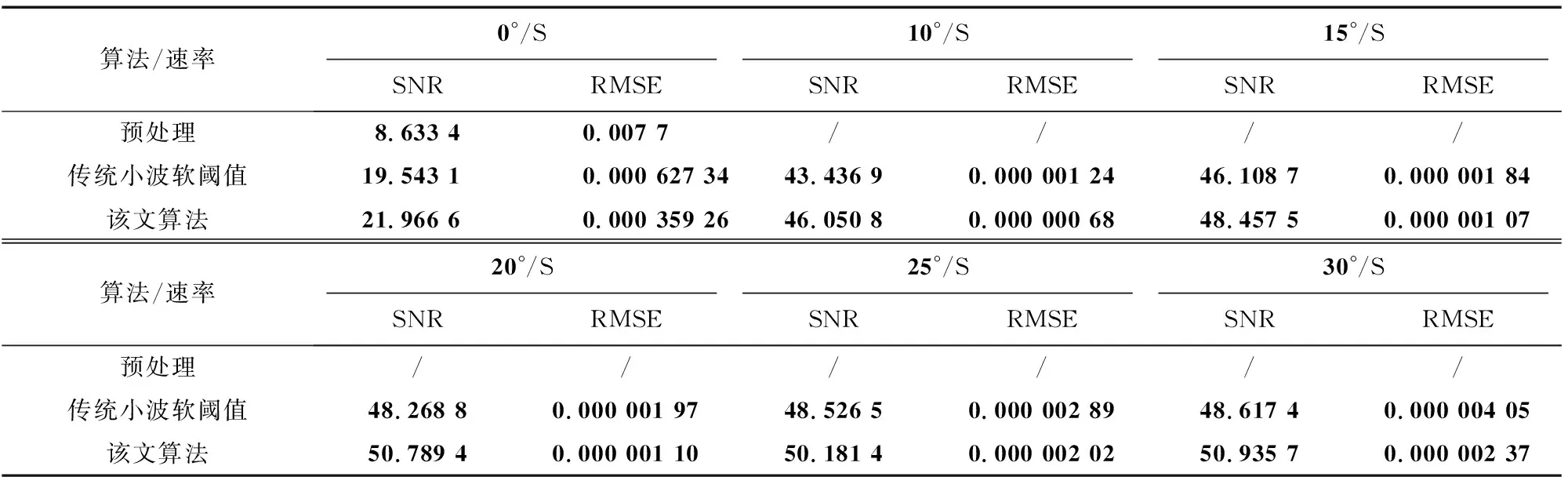
表2 传统小波软阈值与该文算法的降噪性能比较Tab.2 Comparison of traditional wavelet soft threshold and noise reduction performance of the proposed algorithm

4 结 论

针对MEMS陀螺的随机误差，研究分析得其是一种非平稳序列，单一的频域和时域分析法虽可降低大部分噪声，但不足以剔除较微弱的噪声信号。陀螺随机误差呈现短期可预测的特性，而且随着时间的增长其随机漂移因蕴含较多细节特征呈现不可预测特性。

SVD/小波的降噪算法在频域和时域上都有较好分析能力，将SVD引入小波变换消噪过程中，通过奇异值重新构建小波系数的谱分配规则以选取子空间重构来实现信号在小波域中的SVD滤波，可最大程度上保留有用信息，剔除微弱噪声，相比较传统小波软阈值算法，SVD/小波在处理信号的细节部分上凸显优势。