一个新三维混沌系统及其自适应滑模同步控制

鲜永菊，扶坤荣，吴周青，徐昌彪

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 光电工程学院，重庆 400065)

0 引 言

混沌是确定与不确定、规则与非规则、有序与无序融为一体的现象，是非线性系统中所特有的一种运动形式，在电子信息工程、生物医药工程、动力学工程等领域中有着广泛的应用前景[1-4]。

自麻省理工大学气象学家Lorenz发现第一个奇怪吸引子—Lorenz吸引子以来，人们经过不断的研究与探索，发现了许多新的混沌系统，如Chen,Lü,Bao等。大量研究工作表明，新型混沌系统的发现，能为研究混沌的应用提供理论基础，因此，寻找新型的混沌系统具有重要的研究价值[5]。

具有共存吸引子的系统在工程中有更高的灵活性和可塑性，因此，共存吸引子在许多实际系统中有着广泛的应用价值[6]。在复杂性科学领域，共存吸引子的研究是一项非常有趣和富有挑战性的工作。对于给定的系统参数，现有的混沌系统大多只有一个混沌吸引子，只有少数文献提到具有多个共存吸引子的系统[7-10]。文献[7]提出了一个无平衡存在部分重叠的共存混沌吸引子的三维自治连续混沌系统。文献[8]提出了一个多吸引子共存的新三维自治连续Jerk系统，其中有周期与混沌、混沌与混沌吸引子共存。文献[9]提出了一类含有周期函数的三维混沌系统，其具有无穷混沌吸引子共存。文献[10-11]均提出了一个新的四维混沌系统，其中有周期与周期、周期与混沌、混沌与混沌吸引子共存。文中所提系统具有与上述文献不同的和平共存复杂动态行为，具有多种类型的吸引子共存，不同吸引子形态如周期1、周期2、周期4、混沌吸引子均与一个周期1吸引子共存。

本文在Bao系统[12]的基础上提出了一个新的三维自治连续混沌系统，通过相图、李亚普诺夫指数(lyapunov exponent, LE)谱和分岔图对系统的动力学行为进行了研究，发现系统具有复杂的动力学行为，存在多种类型的吸引子共存。通过拓扑马蹄理论和数值计算，得到了系统的拓扑马蹄和拓扑熵，进一步证明了系统的混沌特性。对系统进行了Multisim模拟电路仿真和现场可编程门阵列(field-programmable gate array, FPGA)数字电路仿真实现，验证了系统的混沌特性和可实现性。另外，基于Lyapunov稳定理论，设计了一个自适应滑模同步控制器，仿真结果表明了所设计控制器的有效性。

1 系统的模型及其基本特性

1.1 系统模型

基于Bao系统，本文构建了一个新的三维自治混沌系统，数学模型为

(1)

(1)式中，x，y，z，为系统变量，a=5，b=4，c=14。

根据系统(1)，可得

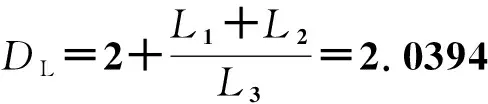
1.2 平衡点及稳定性

令系统方程(1)的左边等于0，即

(2)

求解(2)式，可得系统的平衡点为

S0=(0,0,0)

S1=(6.132,4.965,2.175)

S2=(6.132,-14.098,-6.175)

S3=(-9.132,11.977,-7.812)

S4=(-9.132,-5.845,3.812)

(3)

令det(λI-J)=0(I为单位矩阵)，得到其特征方程为

f(λ)=λ3+A1λ2+A2λ+A3=0

(4)

(4)式中，

A1=b+c-a

当a=5，b=4，c=14时，其平衡点的稳定性如表1。

表1 平衡点的稳定性Tab.1 Stability of equilibrium points

1.3 动力学特性

取a=5，b=4，初始值为[1,1,1]，选择c作为控制参数，时间步长Δt=0.001，迭代时间从t=0到t=200。采用文献[12]所提方法以及四Runge-Kutta算法，分别计算出系统(1)的Lyapunov指数谱和分岔图，如图2、图3。可以看出，Lyapunov指数谱和分岔图能较好地吻合，该系统具有丰富的动力学行为。

当c从8向10增加时，系统(1)通向混沌的道路为倍周期分岔道路。当c=8时，为周期1轨道；当c=9.28时，为周期2轨道；当c=9.6时，为周期4轨道；当c=9.8时出现混沌吸引子，其LE分别为0.319 2，0.003 7和-9.122 9。

当c从12.2向11.8减小时，系统(1)通向混沌的道路为倍周期分岔道路，表现为倒分岔。当c=12.18时，为周期1轨道；当c=12.08时，由周期1轨道变成了周期2轨道；当c=12和c=11.8时出现混沌吸引子，其LE分别为0.306 4，0.002 5，-11.308 9和0.585 5，0.002 1，-11.387 6。

图4a～图4h分别给出了系统在上述参数下对应初始值为[1,1,1]和[-1,-1,-1]的相图，其中初始值为[-1,-1,-1]时均为周期1吸引子，而初始值为[1,1,1]时出现周期1、周期2、周期4和混沌吸引子，即周期吸引子与周期吸引子、周期吸引子与混沌吸引子共存的情况。

2 系统中的拓扑马蹄与拓扑熵

令D是度量空间A的紧子集，f:D→A是一个满足存在D的m个互不相交的连通子集D1,D2,…,Dm，且对于每个Di都有f|Di连续。

定义1[13]对于任意1≤i≤m，令D1i和D2i为Di的2个互不相交的紧子集，对于Di的一个连通子集，若h∩D1i≠∅和h∩D2i≠∅，则称h连接D1i和D2i，表示为(D1i↔D2i)。

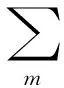
σ(q)=(…,q-n+1,…,q0,q1,q2,…,qn+1,…)

取参数az=-0.3，初始条件为[2,2,2]。选取的Poincare截面为Π={(x,y,z)|z=0}，选择相应的庞加莱映射H：Π→Π如下：对每个(x,y,0)∈Π,H(x,y,0)是系统(1)在初始条件(x,y,0)的流下的第一回归映射。使用HsTool工具箱中一个名为“A toolbox for finding horseshoes in 2D map”的Matlab GUI程序来寻找拓扑马蹄，寻找拓扑马蹄的详细方法可参考文献[15-16]。经过多次尝试，找到了一个拓扑马蹄如图5，其马蹄映射如图6。

其中，D1的4个顶点坐标为

(6.908 921 933,13.331 018 519)
(7.507 434 944,12.729 166 667)
(8.704 460 967,13.655 092 593)
(8.210 037 175,14.141 203 704)

D2的4个顶点坐标为

(9.328 996 283,14.743 055 556)
(9.797 397 770,14.256 944 444)
(9.276 951 673,13.909 722 222)
(8.704 460 967,14.303 240 741)

3 系统的电路实现

3.1 Multisim模拟仿真电路实现

采用线性电阻、电容、LM2924N型运算放大器、MULTIPLIER模拟乘法器，其中乘法器的输出增益为0.1，从而设计出了系统(1)的模拟电子电路，如图7。

根据电路图以及电路理论，可得电路方程为

(5)

(5)式中，R1～R20为电阻，C1～C3为电容。取电容C1=C2=C3=1 μF，电阻R3=R5=R13=100 kΩ。令R4=R8=R9=R10=R14=R15=1 kΩ，对比系统(1)中的系数，可得R1=R19=12 kΩ，R2=30 kΩ，R6=R20=14 kΩ，R7=10 kΩ，R11=20 kΩ，R12=R17=40 kΩ，R16=50 kΩ，R18=200 kΩ。图8为示波器上观察到的结果，可以看出，实验结果与数值仿真结果完全相符。

3.2 FPGA数字仿真电路实现

由于模拟器件的性能容易受到环境温度、湿度以及器件老化的影响，故模拟电路实现混沌系统会严重影响系统的动力学特性，限制了模拟混沌电路在工程中的应用。采用FPGA数字电路技术实现混沌系统可以很好地避免这些问题，可以保证混沌吸引子的稳定可靠，且FPGA以其强大的运算能力而被采用。

由于该系统是连续时间系统，FPGA无法直接处理。采用Euler算法将系统(1)离散化，得到的差分方程为

(6)

(6)式中，离散采样时间步长取ΔT=0.001，用定点小数与截位计算相结合的方式对离散化方程中的实数进行处理，使其在FPGA中正确运算。通过板级验证以及变量比例压缩，通过Xilinx的FPGA开发软件Vivado进行设计，在FPGA开发板上实现了系统(1)，实验结果如图9，其与Multisim软件仿真以及计算机仿真结果一致。

4 系统的自适应滑模控制

考虑如下受控系统

(7)

定义滑模函数

(8)

(8)式中，e=z-r为跟踪误差，r为理想位置信号，k>0。

设计自适应控制器为

(9)

(10)

对参数估计误差(10)求导得到

(11)

定义Lyapunov函数为

(12)

对V求导，将(9)—(10)式代入，得

b(xy+y2)-c(kz+xy-cz))-

(13)

参数更新定律如(14)式，则

(14)

根据Lyapunov稳定性定理，可知受控系统(7)的平衡状态是全局渐进稳定的。

5 结束语

本文设计了一个新的三维自治连续混沌系统，通过数值仿真研究了系统的基本特性，发现系统存在周期1与周期1、周期2、周期4和混沌吸引子共存的复杂动力学行为。通过数值计算，得到了系统的拓扑马蹄，其拓扑熵为ent(f)=(1/6)log2，进一步证明了该系统的混沌特性。对系统进行了模拟电路和数字电路的仿真实现，验证了系统的混沌特性和可实现性。基于Lyapunov稳定理论设计了一个自适应滑模同步控制器，实现对给定信号的追踪与未知参数的辨识，并且通过数值仿真证明了控制器的有效性。