基于预编码改进的多载波系统ICI消除方案
2020-05-01王薇,梁燕
王 薇,梁 燕
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
随着互联网和物联网的飞速发展,以及新业务的不断涌现,移动通信对频谱、速率、容量和灵活性等方面的需求越来越高[1-2]。为了满足这些需求,必然需要全新的相关技术以实现高频谱效率、高速率、超可靠低时延的通信以及巨大的设备连接密度等[3]。无线空口波形作为一项基础传输技术同样需要更新换代以提供更加灵活高效的传输能力[4]。目前对空口新波形的研究主要分为2类:①基于第4代移动通信的正交频分复用,例如滤波正交频分复用[5],通用滤波多载波(universal filtered multi-carrier,UFMC),加窗正交频分复用(windowed orthogonal frequency division multiplexing,W-OFDM)等;②采用与OFDM不同的收发端结构,例如滤波器组多载波(filter bank multi-carrier,FBMC)和广义频分复用(generalized frequency division multiplexing,GFDM)等[6]。其中,第1类方案可统称为OFDM-based多载波系统,其核心思想是针对OFDM波形旁瓣过高的问题,通过时域加窗/频域滤波等技术抑制OFDM信号的旁瓣,提高频谱利用率。OFDM-based 类方案因其在OFDM技术基础上的自然演进,得到业界普遍认可。然而,与OFDM类似,OFDM-based类方案子载波间要求严格正交,对系统频偏敏感。实际应用中存在的收发端载波频率偏移,传输过程中的多普勒效应等均会导致严重的子载波间干扰[7]。另外,在大规模机器类型通信场景,波形设计需放宽同步要求[8],因此,如何消除载波间干扰是未来多载波系统中不容忽视的研究内容。
除了诸如ICI自消除[9]、频域均衡等技术之外,近年来学术界已经提出了包括频域预编码(precoding)在内的许多新的ICI消除技术。与其他技术相比,预编码技术无需引入任何对信号的非线性处理,且实现简便,不会显著损失系统误码性能,因而具有良好的应用前景。预编码技术作为一种针对多载波系统缺陷研究的优化技术,在数据进入快速傅里叶变换(inverse fast Fourier transform,IFFT)前对数据进行编码,重塑信号,使其具有理想特性或达到某种特定需求,如抑制ICI和旁瓣[10]、降低峰均功率比(peak to average power ratio,PAPR)[11]等,然后在接收端对数据进行解码,还原数据。文献[12]首次在OFDM系统中应用频域预编码,并提出一种相关多项式(F(D)=1-D)预编码方案,显著降低OFDM系统因频偏产生的载波间干扰,该方案本质是将同一数据以相反符号调制到两相邻的子载波,同一子载波上既包含前一符号,又包含原符号,从而不会牺牲频谱利用率。另外,在实际应用中,预编码方案已经应用于基于3GPP-LTE标准的上行链路单载波频分多址接入技术(single-carrier frequency division multiple access,SC-FDMA)[13],该方案通过加入离散傅里叶变换(discrete Fourier transform,DFT)矩阵作为预编码器,实现了上行链路中对PAPR的抑制。文献[14]将SC-FDMA中所用的DFT矩阵应用到UFMC和F-OFDM波形中,在一定程度上降低了PAPR。
本文基于多载波通信和预编码设计的理论基础,首先针对OFDM-based系统,提出了统一的预编码应用模型。其中,通过灵活地选择不同的预编码方案和不同的波形调制,可以得到多种OFDM-based系统实例和不同的系统优化结果。同时,针对频偏对OFDM-based系统的性能影响给出了分析方法,基于发送和接收成型脉冲的互模糊函数对信号和载波间干扰进行量化分析,然后利用原始信号的统计特性得到预编码后系统的载干比。另外,基于本文模型,分析在频偏环境下F-OFDM实例的载波间干扰因子是否具有和OFDM系统相同的特性,并将现有针对OFDM设计的预编码方案应用于F-OFDM系统,进一步分析方案可获得的载干比。最后,本文进一步提出了一种基于双向抵消ICI思想的预编码方案,此方案将目标载波2个方向的多个子载波加权进行ICI抵消,比传统方案抵消的干扰更多,可以得到更好的抗频偏能力。仿真结果表明,无论在OFDM系统还是F-OFDM系统中,所提出的方案都比传统的预编码抑制ICI方案能更好地改善系统载干比性能。
1 预编码模型
图1为一个OFDM-based系统应用预编码技术的简易模型框图。
在信号生成端,假设数据源每Ts时间同时且独立地产生M个复数据符号,采用矩阵的形式定义符号长度为M的原始符号块为
(1)
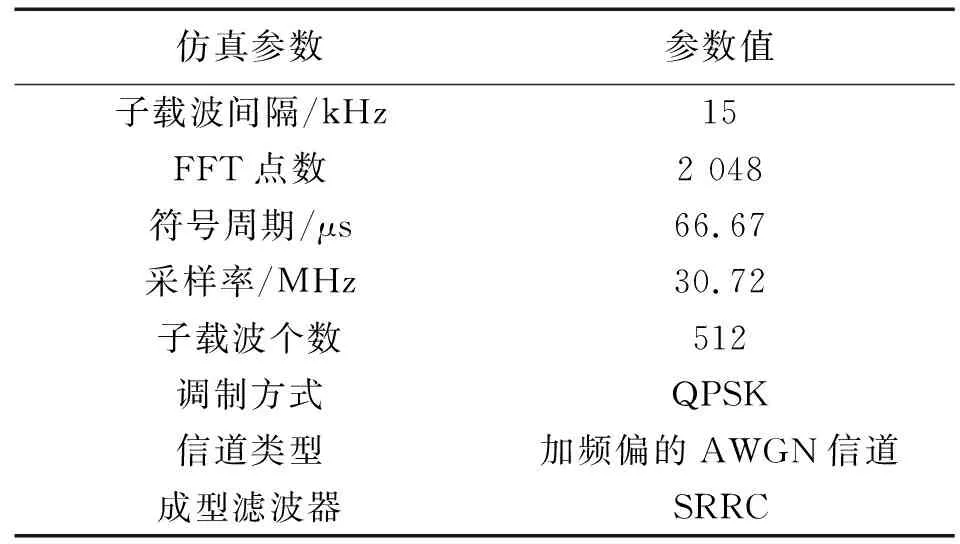
(1)式中,矩阵元素{Dm,k}M-1m=0表示第k个时间间隔kT-Tg-Td/2≤t 预编码矩阵定义为 (2) 预编码器将通过(3)式对原始符号块进行预编码,得到长度为N的新符号块,并重塑信号。 B=GD=[·]N×M[·]M×K= (3) 预编码器输出的复数符号块B随后进行快速傅里叶逆变换,通过调制过程产生多载波信号,利用N个子载波{F0+nF;n∈ZN}传输,时域连续基带发送信号可以表示为 pn(t-kT) (4) (4)式中:-Tg-Td/2≤t b(α)ψ(t-α)dα (5) 实例1 如果设置b(·)=δ(·),那么βn=1,则pn(t)=ψ(t),此时,s(l)为一个标准的OFDM信号。 离散化(4)式,以Δt为时间间隔抽样,得到离散基带发送信号为 kLΔt)}}×p(lΔt-kLΔt) (6) (6)式中,L表示在一个符号周期内采样点数。频带信号为 (7) (7)式中,F0>>F。 为了精确分析频偏在此系统中的影响,本文假设其他条件都是理想的,系统只存在归一化频率同步偏移ε,因此,信号经过信道后的接收信号为 y(l)=s(l)exp(j2πεl/N)= exp(j2πεl/N)×p(l-kL) (8) 在接收端,信号经过接收滤波及FFT解调出第i个子载波,第k′时间间隔上的数据为 b1+b2+b3 (9) 最后,接收符号块可通过预编码逆矩阵进行解码,还原原始符号块为 (13) 在第1节的OFDM-based预编码统一模型中,提到可以通过灵活改变pn(t)得到不同的多载波系统实例,同时可以针对需求选择预编码方案达到不同的系统优化效果。以下本文只针对消除ICI为优化目标,分别理论分析预编码方案在模型OFDM和F-OFDM中消除ICI的原理。 本文假设原始发送信号具有零均值和非相关特性,并且符号等能量为σ2=1,即满足E[Dm,k]=0,E[Dm,kDi,k′]=δm-iδk-k′σ2。由于只考虑频偏对系统的性能影响,则系统接收信号只存在有用信号部分和载波间干扰部分,不存在符号间干扰,即k′=k,则(12)式中函数Ap,g(k′-k,i-n-ε)(以下简写为Ap,g(i-n-ε))反映了第n个子载波对第i个子载波的干扰,称其为子载波干扰系数。 图2给出了子载波数为16的OFDM系统(p(t)和g(t)为矩形窗),i为0时,函数AOFDMp,g(i-n-ε)的幅值例子,频偏值分别为0.2和0.3。由图2可以观察到,子载波指数n为0时,函数AOFDMp,g(i-n-ε)取得最大值,此时i=n,因此,不存在载波间干扰。而子载波指数n从1~15时,可以观察到第1个子载波和第15个子载波的干扰系数远高于其他载波,这说明目标载波i的相邻载波是造成ICI的主要原因。另外,AOFDMp,g(-ε)随着频偏的增大而减小,而ICI部分随频偏增大也越来越严重。同时,图2中显示2个相邻的子载波干扰系数间变化是非常小的,即第a个子载波和第a+1个子载波对同一个子载波的干扰是相差不大的。 因此,有作者根据此理论提出ICI自消除方案,该方案将同一数据以相反的符号调制到两相邻的子载波,编码规则为D1,k=-D0,k,D3,k=-D2,k,…,DN-1,k=-DN-2,k,则解调第i个子载波的接收信号变为 n-i-ε)] (14) 此时,系统的子载波间干扰系数变为AOFDMp,g(i-n-ε)-AOFDMp,g(i-n-i-ε),即第n个子载波和第n+1个子载波对第i个子载波的干扰可以相互抵消掉一大部分。基于其本质分析,ICI自消除技术也是一种预编码方案,其预编码矩阵可以描述为(15)式,记作Gself-cancelling。ICI自消除方案虽然是抑制ICI行之有效的方法,但是其频谱利用率只有50%。 为了进一步提高ICI抑制方案的频谱利用率,多项式(F(D)=1-D)预编码方案被提出,该方案的本质也是将同一数据以相反符号调制到两相邻的子载波,但是同一子载波上既包含前一符号,又包含原符号,从而不会牺牲频谱利用率。用矩阵形式描述此方案如 (16)式,记作G1-D。 (15) (16) 若系统采用经典的多项式预编码方案,由(12)式可知,在计算解调输出信号中ICI部分的功率时,此方案应当考虑Bk和Bk±1之间的相关性, E[BnBp]= (17) 由于函数AOFDMp,g(i-n-ε)为周期函数,不失一般性,假设i=0,由(17)式可以得到解调输出的信号各部分能量为 E(b1b*1)=2σ2|AOFDMp,g(-ε)|2 (18) AOFDMp,g(-n+1-ε)AOFDM*p,g(-n-ε)] (19) (20) 进一步,在上述预编码OFDM系统的基础上加入滤波,得到F-OFDM系统。图3给出了子载波数为16,i为0时,函数AF-OFDMp,g(i-n-ε)的幅值例子,频偏值分别为0.2和0.3。 由图3可以观察到F-OFDM系统中,子载波指数n为0时,函数AF-OFDMp,g(i-n-ε)取得最大值,而子载波指数n从1取值到15时,可以观察到第1个子载波和第15个子载波的干扰系数远高于其他载波,这说明目标载波i的相邻载波是造成F-OFDM系统ICI的主要原因。同时,图3中显示2个相邻的子载波干扰系数间变化非常小,即第a个子载波和第a+1个子载波对其他子载波的干扰相差不大。这些特性与2.1节中OFDM系统的干扰因子特性类似,因此,本文尝试将OFDM系统中的预编码抑制ICI方案应用到F-OFDM系统中。若在F-OFDM系统中应用多项式预编码方案,可以得到系统载干比为 (21) (21)式中, σ2[AF-OFDMp,g(i-n-ε)AF-OFDM*p,g(i-n+1-ε)+ AF-OFDMp,g(i-n+1-ε)AF-OFDM*p,g(i-n-ε)] (22) 上述的预编码方案是根据相邻子载波干扰系数之间变化极小的特性,利用相邻子载波对同一个目标子载波的干扰可以相互抵消来设计预编码矩阵。但是,现有方案只利用了1个方向的相邻2个子载波相互抵消,而没有考虑子载波相邻2个方向的子载波均可相互抵消。将需要发送的数据映射到2个方向加权的子载波组上,子载波干扰系数与两边的子载波干扰系数加权后差值更小,即可抵消更多干扰。因此,本文基于OFDM-based多载波系统提出了一类2个方向抵消ICI的预编码方案。 采用列向量的形式定义符号长度为N的原始符号序列为[D0D1D2…DN-1]T,将符号序列中每个符号分别减去相邻两边共Q+1个符号的权值,其中,第1个到第「Q/2⎤个符号不变,得到预编码后的新符号序列。则Q阶的双向预编码方式如图4。 预编码过程可以描述为 (23) (23)式中:「·⎤和⎣·」分别表示向上取整和向下取整;W为[「Q/2⎤,N-⎣Q/2」-2]中的整数集合;CBA表示从A中取B的组合数。 考虑Q=1时的双向预编码方案特例,将符号序列中的每个符号分别减去相邻的2个符号的权值,其中第1个符号不变,得到预编码后的新符号序列,预编码过程可描述为 (24) 由(12)式可知,计算解调输出信号中ICI部分的功率时,此方案应当考虑Bk,Bk±1,Bk±2之间的相关性。 (25) 假设i=0,并由(10)式、(12)式和(25)式可得有用信号的功率和ICI的功率分别为 E(b1b*1)=6σ2|Ap,g(-ε)|2 (26) [Ap,g(-n-ε)A*p,g(-n+1-ε)+ Ap,g(-n+1-ε)A*p,g(-n-ε)]+ Ap,g(-n+2-ε)A*p,g(-n-ε)] (27) (28) 为了更好地分析上述预编码方案对多载波系统带来的抗干扰增益,本节使用MATLAB对系统进行仿真,仿真参数如表1。 图5给出了在OFDM系统中应用一阶双向预编码方案时解调输出信号的各部分能量,且由图5中的结果可以看出,在频偏小于0.4个载波间隔时,解调输出以有用信号的能量为主,由于选择的符号能量为1,所以频偏为0时,系统输出只有0 dB的信号能量。频率同步偏移超过0.7个载波间隔时,解调输出以ICI干扰为主。 表1 仿真参数Tab.1 Simulation parameters 在频偏环境下,对于未编码的多载波系统,它的CIR表达式为 (29) 利用(20)式、(28)式和(29)式可以得到图6的仿真结果,分别为采用双向预编码、采用多项式型预编码和未编码时的OFDM系统CIR,且仿真实验分别选择了Q为1和2时的预编码方案进行比较,可以看出,随着频偏的增加,系统的载干比下降。具体来说,当归一化频偏为0.15~0.35时,这3种预编码方案在未编码的OFDM系统基础上为系统提供了约3.5~5 dB的CIR性能改善,而在频偏超过0.45之后,改善的效果开始趋于下降。系统频偏小于0.25时,双向型预编码方案的系统载干比在10 dB以上,当频偏大于0.55时,系统输出的载干比小于0 dB,此时,干扰能量已经掩盖了有用信号能量,因此,已经无法解调出正确发送数据。同时,在3种方案之间,2种双向型预编码较多项式预编码取得的CIR值提高了约0.7 dB,且二阶双向预编码对系统CIR性能的改善较一阶稍微有所提高。 图7分别为未编码、采用多项式型预编码及采用双向预编码时的F-OFDM系统CIR仿真结果,可以看出,频偏小于0.4时,所述3种预编码方案在未编码的OFDM系统基础上为系统提供了约3.5~6 dB的CIR性能改善,而在频偏超过0.4之后,改善的效果开始趋于下降。当系统频偏小于0.27时,双向型预编码方案的系统载干比在10 dB以上。与OFDM系统相同,在3种方案之间,2种双向型预编码均较多项式预编码取得的CIR值更高,且二阶双向预编码对系统CIR性能的改善较一阶稍微有所提高。 图8对比了在OFDM系统中采用双向型预编码方案的一阶到四阶特例,由图8中可以看出,随着阶数的增加,系统的CIR值也会有所改善,系统的抗频偏能力得到提高。同时,随着Q的增加,CIR值的提升效果趋于下降,得到的性能改善越来越少,且系统的复杂度越来越高。因此,可以根据系统的要求选择不同阶数的预编码方案,达到不同的系统抗频偏性能。 图9是OFDM系统分别采用传统预编码方案和二阶双向型预编码方案在加性高斯白噪声(additive white gaussian noise,AWGN)信道中的误比特率曲线图,且已假设归一化频偏为0.3。可以看出,在高信噪比条件下,所提方案较传统方案BER性能更好,而在低信噪比条件下,性能只有稍微的损失。 系统的复杂度是由计算发送端与接收端复数信号的乘法次数和加法次数得到。根据本文系统模型可知,生成发送和接收信号所需的IFFT/FFT需要2NlbN次实数乘法运算,3NlbN次实数加法运算。一般预编码在发送端和接收端需要进行矩阵相乘,需要2N3次乘法运算。而考虑本文方案的二阶形式,由于矩阵中元素大多为0,经过运算简化只需要14(N-2)次加法运算。因此,本文方案较少地增加了系统的复杂度即可获得良好的抗干扰性能。传统OFDM系统和二阶双向型预编码系统的复杂度如表2。 表2 采用预编码和未编码OFDM复杂度对比Tab.2 Complexity of OFDM with/without precoding 本文针对OFDM-based多载波系统,首先提出了一种统一的预编码应用模型,该模型可以通过配置预编码方案和多载波调制方式得到多种系统实例,并针对频偏对此系统的性能影响给出了分析方法。另外,提出了一种新的基于双向消除ICI的预编码优化方案,然后理论分析在OFDM实例和F-OFDM实例中此方案可获得载干比的提升,最后通过进一步的仿真验证了这种方案在本文统一模型中的可行性。仿真结果显示,该方案在模型OFDM和F-OFDM实例系统中相比于未进行预编码的系统分别可以获得最多约5 dB和6 dB的CIR性能改善。另外,本文的统一模型还可以扩展到其他新型多载波方案,即灵活配置模型中的参数和窗函数等,可以得到不同的基于OFDM的多载波调制方案,由于篇幅有限,本文未进行讨论。



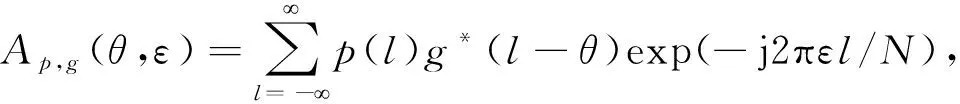
2 预编码抑制ICI
2.1 OFDM
2.2 F-OFDM
3 双向型预编码
4 性能分析

5 结束语
猜你喜欢
杂志排行
