运用数形结合思想提高高中数学解题能力的初探

■张莉娟

高中数学在很大程度上决定着高考成绩的高低,高中数学知识的学习对于很多同学来说存在一定的困难,因为需要对大量的数学概念进行记忆和应用,而数形结合的渗透,会帮助大家更好地掌握基础知识,为同学们高考成绩的提升提供保障。下面就来探讨数学学习中如何使用数形结合思想。

一、应用数形结合思想解题的好处

同学们在学习高中数学知识的过程中,认识到数形结合思想的重要性,并在实际学习中充分应用是非常必要的。如图1 所示,U为全集,其中的子集为M、P、S,阴影部分的代表集合也就一目了然了。

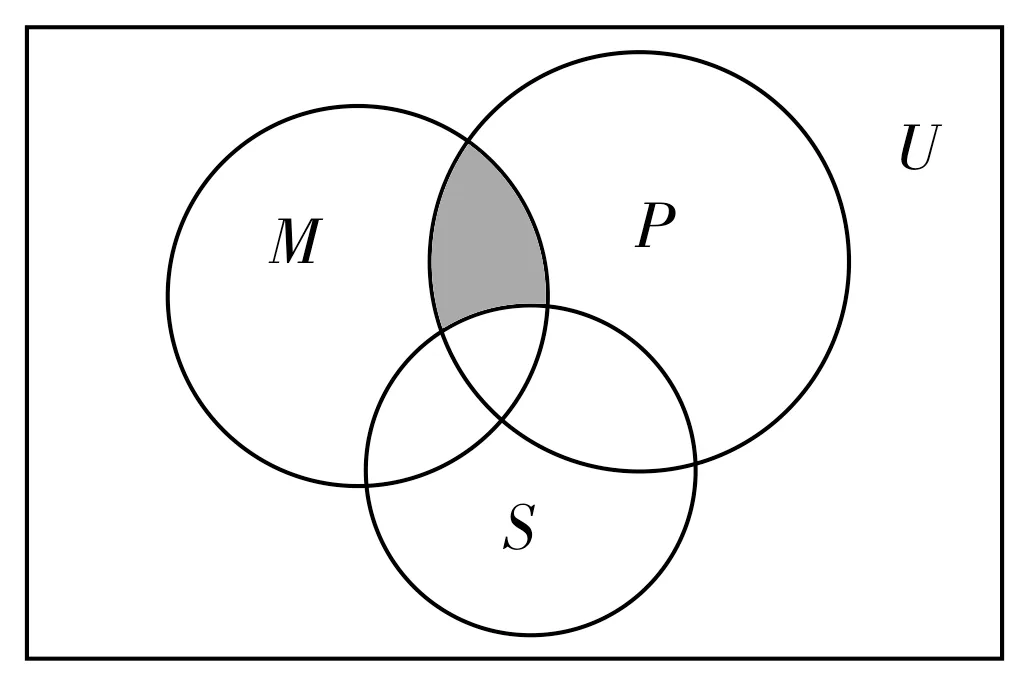
图1

例如,求关于x的不等式：。在对该题进行解答时,因为需要对a的情况进行分析,所以可利用数形结合方法,如图2所示。

(1)当a=0时,集合为(-∞,0)∪(0,+∞)。

(2)当a＞0时,集合为。

(3)当a＜0时,集合为。

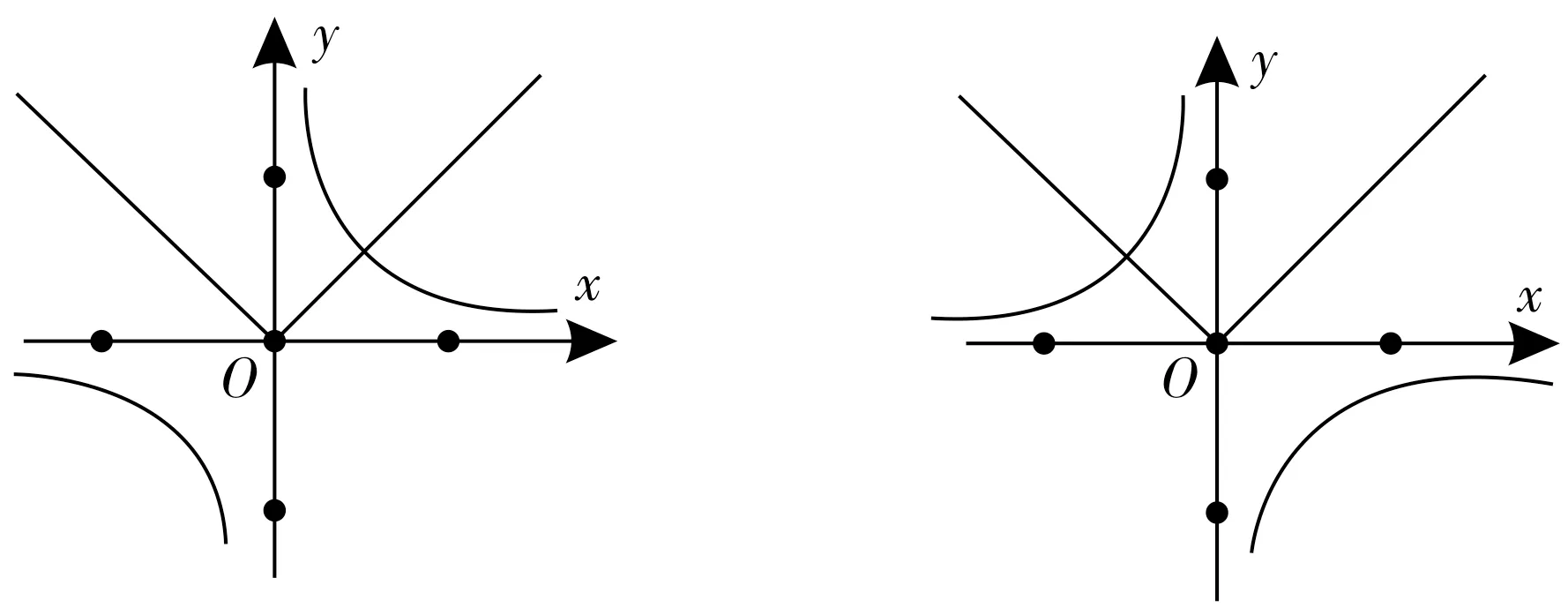
图2

二、数形结合思想在高中数学学习中的应用

(一)促使同学们形成图形意识

在数学的学习过程中,同学们需要具备图形意识,如刻度尺上的刻度、绳子上的结、座位和每天行走的路线等；实数含有无数个,分为正数、负数、零；直线的组成是无数点的集合,所以在直线上可以将实数表现出来等。

例如,已知0＜a＜1,求方程的实数根的个数。如图3所示,判断图像y=a|x|与y=|logax|的交点个数,可以画出两个函数的图像,该图像有两个交点,所以方程有两个实根。

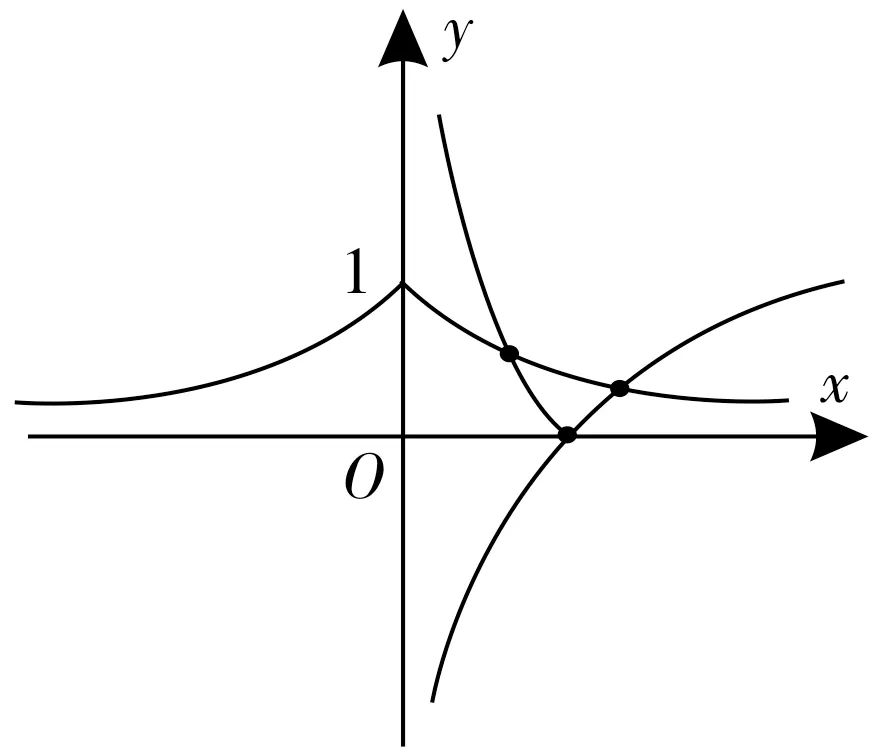
图3

再如,设F1、F2分别为双曲线的左、右焦点,如果双曲线上存在点A,∠F1AF2=90°,且,求双曲线的离心率。基于对图像的分析,得。基于双曲线的定义,由。在Rt△AF1F2中,通过勾股定理,得9a2+a2=4c2,故双曲线的离心率。

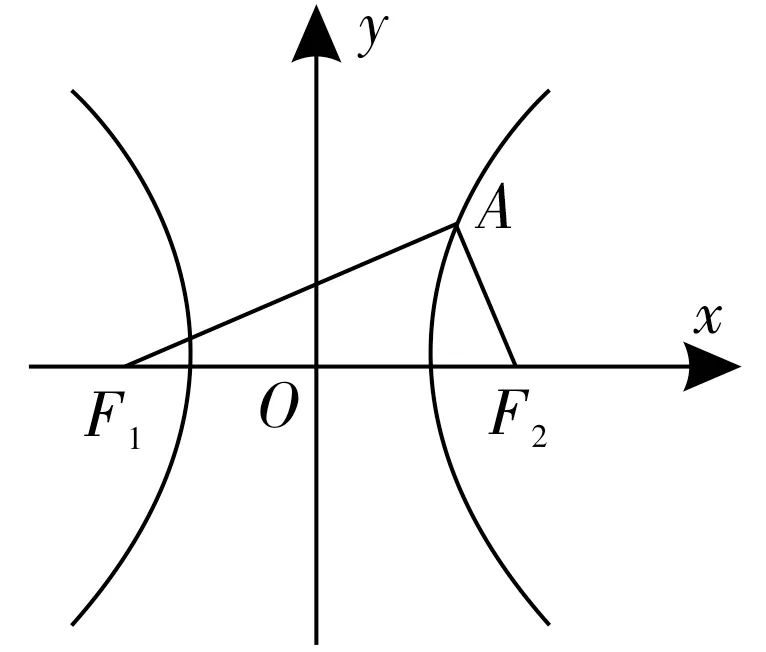
图4

(二)促使同学们更新学习观念

同学们在学习高中数学的过程中,不仅要接受知识,对其进行模仿和练习,还需要积极渗透更多的学习方式,如合作交流学习、自主学习等。同时,还要积极探索数形结合的实际应用,促使思维模式的形成,保证为数学问题的解决提供充足条件。

例如,设函数f(x)=ax3+bx2+cx+d的图像如图5 所示,求f(-1)+f(1)的值。图像过原点,d=0。f(x)的图像和x轴的三个交点结合,分别为-x1,0,x2,设f(x)=ax(x+x1)(x-x2)=ax3+bx2+cx,在x＞x2时,a＜0,b=a(x1-x2),b＞0。所以f(-1)+f(1)=2b。

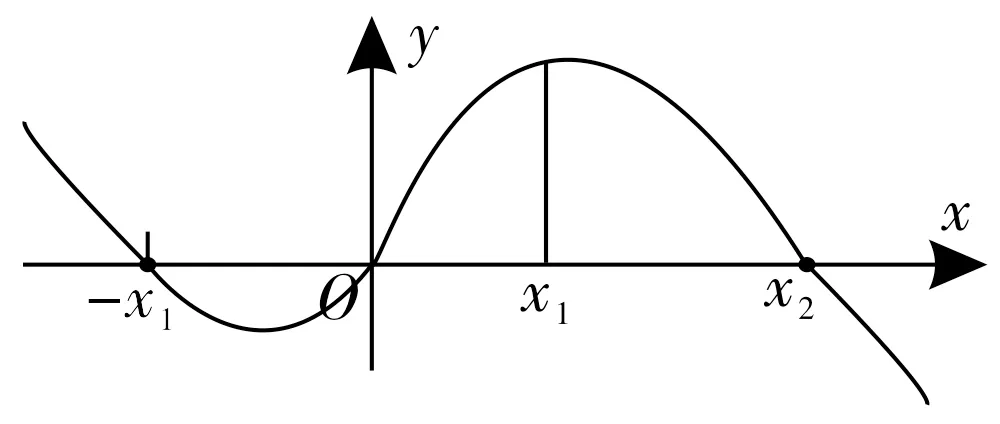
图5

总之,同学们在学习高中数学知识的过程中,为了充分应用数形结合思想,需要不断加强对数形结合的认识。同时,还要不断总结有效的学习方法,对学习方式进行不断的创新。这样数学问题的解决能力才能得到极大的提升。