聚焦核心素养,提升逻辑推理能力——由一道试题引出的多种分析策略

■艾升东

我们在复习时发现这样一道试题,可以从不同的角度来解答,现呈现给大家。

例题如图1 所示,设双曲线C：的一个焦点为点F,过F作双曲线C的一条渐近线的垂线,垂足为点A,且与另一条渐近线交于点B,若,则双曲线C的离心率为____。

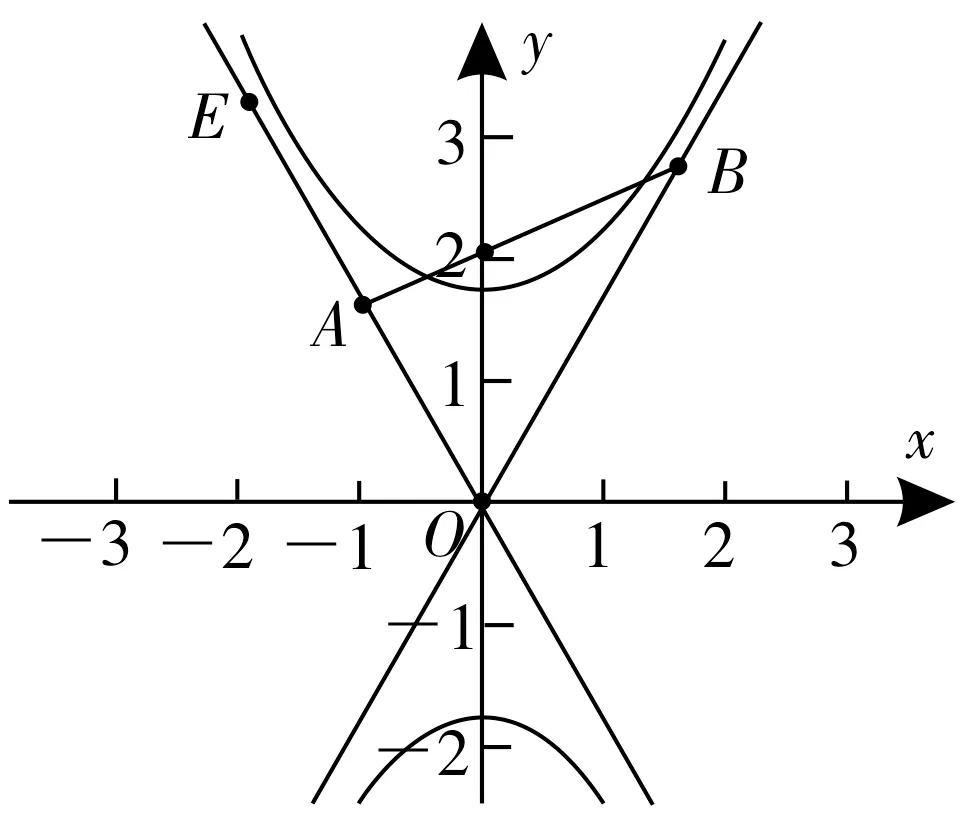
图1

思维方式一：由焦点F写出F的坐标。过点F作双曲线C的一条渐近线的垂线,可以用点斜式写出直线方程。因为垂足为点A,所以联立两直线方程,求出A的坐标。又由与另一条渐近_线交于点B,可求出点B的坐标。最后由3,用向量的坐标形式表示,得到a,b,c的一个齐次式,解出e。

点评:该思维方法对题目逐句分析,逻辑思维清晰,若是解答综合题,应该来说是一种很正规的方法。但是,对于填空题来说,如果完成全部计算,至少需要10min以上,费时、费力。请同学们思考一下“3这个条件,我们能否从几何方法上突破呢?

思维方式二：思考片刻后,有一个同学发现该条件可以变为,得出A,B,F三点共线,进而得到。而渐近线所夹的轴其实是角平分线,由角平分线定理得|OB|∶|OA|=2∶1。因为△OAB是直角三角形,从而得到∠AOB=60°,∠BOx=60°,所以直线OB的正切=,从而得到e。

思维方式三：另一个同学又提出,既然要得到这个关系式,我们可以直接从3转化到。其余过程同上。

思维方式四：又有一名同学提出,本题是向量之和,如果我们延长为其2 倍至E点,依托作平行四边形,y轴是∠BOA的平分线,所作的平行四边形就是一个菱形,OE=OB。A是OE的中点,BA⊥OE,所以OB=EB,△OBE为等边三角形,渐近线的倾斜角为60°。其余过程同“方式二”。

点评:以上几位同学善于思考,抓出了三点共线原理及角平分线定理,能由垂直中点想到等腰及由直线角度联想到正切,说明这几位同学的综合分析能力较强。

思考：我们注意到,最开始的同学采用的方法体现了数学核心素养中的运算能力,若是解答题,该方法中规中矩,可以尽可能地有效得分。但在解答选择题和填空题时,我们更要注重数形结合思想的运用,尽量多思考,简化运算。同学们在做题时,要学会发散思维,多角度、多层面地思考问题,逐步提高发现问题、分析问题、解决问题的能力,注重数学核心素养的培养,以应对即将到来的新高考。