原子时算法分析与对比
2020-04-30罗亚雄
王 锐, 袁 静, 班 亚, 杨 帆,罗 浩, 江 力, 罗亚雄
(1.重庆市计量质量检测研究院,重庆 401123; 2.瑞士洛桑联邦理工大学, Lausanne, CH 1015,Switzerland)
1 引 言
计算国际原子时的算法是为了保证得到一个可靠,长期稳定和准确的时间尺度。近些年随着全球各地的高性能原子钟的引入,使得地方原子时时间尺度以及国际原子时(international atomic time,TAI)的准确程度越来越高。但是随着硬件设备的性能瓶颈,原子时的算法改进则成为提高原子时的主要方向之一。ALGOS是最经典的加权算法,Kalman滤波算法解决了噪声强弱的影响,AT1(NIST)算法具有实时性的预测。本文从理论上分析对比了这3种算法。
2 原子时ALGOS算法
原子时的经典算法ALGOS是由国际计量局(BIPM)设计与开发的一种时间尺度算法,其测量了全球各地实验室的原子钟时间尺度,然后进行加权平均,从而保证优化时间尺度的可靠性、频率的长时间稳定性以及频率的准确性。
2.1 ALGOS算法基本理论
国际计量局计算原子时(TAI)的算法[1~6]主要有以下两个步骤:
(1)计算自由原子时的时间尺度(EAL)。利用ALGOS算法,对世界各地超过400台原子钟的数据进行计算,得出权重平均数。
(2)利用基准频标PFS/SFS校准EAL的频率,从而得到原子时(TAI)。
ALGOS算法是经典的加权平均法,定义原子自由时间尺度EAL见式(1)。
xj(t)=[EAL(t)-hj(t)]
(1)
式中:N代表在周期1个月中参与测试的钟的数量;wi是钟Hi对应的权重值,权重的设定是为了反映长时间的稳定性;hi是钟Hi在时刻t的测量值,为了保障时间尺度的连续性,h′i是对钟Hi的测量值的预测修正量;xi,j是钟j和钟i的相位差。
2.1.1 频率预测算法
频率的预测是为了在有新的钟加入或移出时,避免频率的跳跃和不稳定。
具体的方法为: 在两个连续的时间段Ik-1=[tk-1,tk]、Ik=[tk,tk+1],为保证频率和相位的连续性,需要预测钟Hi在tk时刻的修正量h′i。BIMP对远程的时间数据处理采用的是后置处理模式,获得各个实验室的原子钟的相位差数据。在1个月的测试周期内,每6天产生1个测试数据点, 每个数据点对应的时刻是BIPM对应的UTC 00:00:00,故可以得到原子自由时间尺度EAL与每台钟测量值的差值xi(tk+nT/6),n=0,…,6;然后对这些数据进行最小二乘优化拟合得到钟Hi对于EAL的频率Bi,Ik(tk+T);从而在1个月的周期Ik=[tk,tk+T], 钟Hi的修正量h′i为:
h′(t)=ai,Ik(tk)+Bip,Ik(t)(t-tk)
(2)
式中:i是钟的编号;p是上一段时间预测的参数;ai,Ik(tk)是在tk时刻,钟Hi对于EAL的相位偏差。
ai,Ik(tk)的估计值为:
ai,Ik(tk)=EAL(tk)-hi(tk)=xi(tk)
(3)
Bip,Ik(t)的估计值为:
Bip,Ik(t)=Bi(tk),t=tk+nT/6
(4)
2.1.2 权重算法
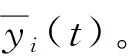

(5)
为了避免获得较大权重的原子钟出现不稳定情况,最大权限制理论[7]提出了一种限制:
wi(t) (6) 式中:wmax为最大权重比例;A是经验常数(经常取2.5)。选择合适的A值,达到利用各原子钟的优点和控制拥有满权因子钟的数量。 2.2.1 新的频率预测算法 在原子时时间尺度的线性频率预测中,假设原子的频率不发生改变,但由于氢钟和铯钟都存在频率漂移,所以线性预测是不够精确的。2011年9月,BIPM增加了对频率漂移量的预测,提出了新的频率预测[8]: (7) 为了估计式(7)的参数,假定在tk时刻,修正量h′i(t)可以写成以下形式: (8) (9) 从式(9)可以看出:频率的漂移量是恒定的,而频率却不再是个定值。 ai(tk)的估计值: (10) Bip,Ik的估计值: (11) EAL(tk)-hi(tk)被用来估计相位和频率,钟Hi关于地球时TT的频率值yTT-hi被用来估计频率漂移。需要假定在1个月的测试期间内,钟的频率漂移保持不变。氢钟和铯钟的漂移量的计算如下: (1)氢钟 (12) (2)铯钟 当采用线性预测模型时,每个月都需要微调修正EAL的频率;而采用新的模型,加入二次项频率漂移量的模型,EAL几乎不需要修正。图1展示了在不同数据长度,不同预报模型条件下,计算得到EAL的稳定度;数据获取的时间是2006年和2008年;从图1可以看出新的二次模型对短期和长期的稳定性都有提高。 图1 不同数据长度、不同模型的自由时间尺度稳定度Fig.1 The frequency stability of the data with different time scales and models 2.2.2 新的权重算法 考虑到在钟的时间尺度系统中,只有钟的编号和它们的预测值不同,BIMP在2014年3月对权重算法提出了新的改进[9],认为可预测的钟才是一个好钟。研究发现如果对频率预测准确,频率漂移和老化等因素不会对EAL的稳定度造成影响。因此,新的权重方法将对频率进行预测,根据各实验室的原子钟的每个月的预测频率和真实频率的差值来预测权重因子,从而保证EAL和UTC的长期稳定性。 算法的具体步骤如下: (1)通过相关的权重集可以得到EAL-hi的值。在第一次迭代中,采用的是上个时间区间所归一化后的权重;后面的迭代采用前一次迭代的值。 (13) (3)计算得到步骤(2)中差值的平方。 (4)计算1年以上的εi,Ik来确保EAL的长时间稳定性。 (5)在计算权重因子时,采用了更具有统计意义的滤波方法进行分配;该方法会分配给新加入的原子钟数值更大的权重。 (14) 式中:j表示计算时间间隔;M表示月份,取值范围是5~12,因UTC的计算至少要5个月的数据,1年是标准的测试周期。 (6)钟的权重因子表达式为: (15) BIMP用新的权重算法对2006~2013年的8年数据进行计算,结果见表1。各原子钟的最大权的个数和占总权重的比例都发生了改变,全世界氢钟最大权重从10%增加到35%,解决了氢钟比例过小,铯钟的权重比例过大的问题,平衡了原子钟权的比例分布。 表1 新旧权重算法权重分布对比Tab.1 Statistics relative to the clock distribution in UTC computation according to the chosen algorithm 计算各时间段的Allan方差,对比得到如表2所示的结果;新的权重方法Allan方差变小,提高了EAL的短时间和长时间的频率稳定性。 表2 新旧权重算法Allan方差Tab.2 The values of the overlapping Allan deviation σy(τ ) 针对ALGOS算法的权重大小与某一种噪声过程的强弱有关的问题,1982年Barnes 提出了Kalman算法。其核心思想是估值理论而不是权重概念,主要是对参考钟和理想时间之差做最佳优化,以估计值为修正量,从而计算时间尺度。Kalman算法的模型是将钟组内的所有单钟模型叠加起来,构成钟组的Kalman滤波器;输入量是钟组各钟与参考钟的钟差测量值,输出量是钟组内所有钟的相位和频率的估计值。本节将详细描述Kalman算法的基本原理。[10~12] 设有N台钟,均符合下述模型: (16) (17) 式中:xi(t)是第t次测量时,钟i的测量值与理想参考钟的差值;yi(t)是它们的频率差值;T是时间间隔;Qi是系统噪声矩阵;ξi是白色调频噪声,方差是Ei;ηi是随机游走调频噪声,方差是Hi。 根据Kalman的滤波原理,钟组的动态模型为: X(t)=φX(t-1)+W(t) (18) 式(18)中各向量具体表示为: 式中:φ为转移矩阵;W(t)为系统噪声矩阵。 测量方程为: Z(t)=HX(t)+V(t) (19) 式中:Z(t)为测量向量;H为测量矩阵;V(t)是测量噪声矩阵。 Kalman的滤波方程组的迭代步骤见式(20): (20) 式中:P为X的误差方差矩阵;Q为系统噪声矩阵;K为Kalman增益;R为测量噪声矩阵。 科研人员采用18台HP5071A铯原子钟的比对数据,TA(Kalman)和TA(ALGOS)的结果相似,长期稳定度相当;但是Kalman算法的不完全性会导致估值结果的误差随时间无穷增大。 AT1算法与ALGOS算法的核心思想都是加权算法;AT1不计算过去频率的真实值,只考虑频率的变化,是实时的计算。基本原理如下[4,12,14]: 在原子钟组中选出稳定性最好的一台钟作为参考钟,将参考钟的频率连接到相位微跃计,通过原子时算法控制微跃器的速率,这样的一种组合等效为一台组合钟,其时间是在每次物理测量完成后计算出来的。 令xi(t),yi(t)分别代表第i台钟相对于组合钟在时刻t的时间差和速率,设τ为测量中的时间间隔,xi(t)、yi(t)都需要预先设定初始值。 这台钟在t+τ时刻相对于组合钟的时间差可以估算为: (21) 式中:yi(t)·τ表示从t时刻到t+τ时刻相对于组合钟的时间变化量。 参考钟相对于组合钟的时间和速率也遵循式(21),区别只是参考钟用角标r。硬件在时刻t+τ测量得到的第i台钟和参考钟的时间差,称之为ti(t+τ)。 参考钟相对于组合钟的钟差就可以通过第i台钟估算得到。 (22) 式(22)表示用第i台钟在t时刻的时间差和速率计算出组合钟相对于参考钟时间差的估算值。 通过之前得到的时间和速率数据,再和现在的测量结果结合,每台钟都可以提供参考钟相对组合钟的时差估算。如果钟有N台,可重复N-1次独立估算,组合钟相对于参考钟的时间可由加权平均得出。 (23) 理想的原子钟时间尺度性质是具有长期稳定性、实时性和准确性,因此,很多算法都使用加权平均组合钟的时间尺度,这就等于增强了时间尺度的稳定性。原子钟时间尺度的噪声也是由各原子钟噪声的线性叠加,这些噪声可以用一些现有的数学模型去可靠地估计。根据前面章节对ALGOS算法、Kalman滤波算法和AT1算法的思路分析,可以得到以下结论: (1)核心思想 ALGOS算法和AT1算法的核心思想是加权平均法,都分配给每台原子钟一个权重,从而增加时间尺度的稳定性;但是没有消除或者抑制原子钟的噪声,不能进一步提高原子时间尺度的精度和可靠性。Kalman算法经过一系列的滤波算法,对于多原子钟上各种噪声进行数学建模从而达到部分的抑制。 (2)稳定性 Kalman滤波算法测得的时间尺度具有长期和短期的稳定性, ALGOS算法主要表明原子钟具有长期稳定性;但Kalman滤波算法的不完全性会导致估值结果的误差随时间无穷增大,在应用Kalman算法时,必须考虑Kalman算法的发散性问题,合理选择估值区间 (3)实时性与应用范围 AT1算法和Kalman滤波算法都具有实时性,而ALGOS是一种滞后算法,因为其测量时间为1个月;带有滞后的算法不适用于很多场景,如卫星导航系统需要实时地预测星载原子钟的状态,并对其做出修正。若滞后1个月来进行修正,卫星钟所积累的误差对于卫星高精度的测距和估时是毁灭性的。因此,AT1算法和Kalman滤波算法适应性相对更广。 本文详细地分析了目前常用的3种基本的原子钟时间尺度的计算方法,从理论上分析了ALGOS算法、Kalman滤波算法和AT1算法数学模型;对比了这3种算法的优缺点,以及其使用范围。结果表明:ALGOS,AT1是加权平均算法,Kalman是滤波算法;AT1和Kalman具有实时性,并且应用范围更广;Kalman滤波算法能更好地处理噪声的影响,适用于卫星导航系统。2.2 新的ALGOS算法

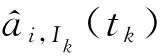
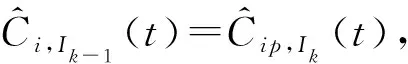
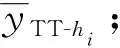

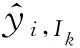

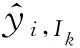


3 Kalman滤波算法
4 AT1算法

5 各算法时间尺度分析与对比
6 结 语
