任意阶次多项式最小二乘拟合不确定度计算方法与最佳拟合阶次分析

许金鑫, 由 强

(1. 中国计量科学研究院, 北京 100029; 2. 清华大学 电机工程与应用电子技术系, 北京 100084)

1 引 言

多项式最小二乘拟合是数据处理中常用的曲线拟合方法。测量不确定度评定的指导性文件(guide to the expression of uncertainty in measurement, GUM)给出了一阶线性最小二乘拟合的不确定度评估方法[1],然而,对于更高阶的多项式最小二乘拟合,却很难从GUM给出的方法中推出其不确定度的理论计算方法。一些其他的评估直线或者平面拟合不确定度的方法,并不适用于最普遍的情况[2～5]。Hibbert在2006年提出了一种相对完备的方法,给出了线性、抛物线和加权线性拟合的不确定表达式[6],然而,三阶以上的多项式拟合仍然很难从这种方法中得到不确定度的表达式。蒙特卡罗法可以用来评估任意阶次的最小二乘拟合的不确定度[7～10]。但这种方法只适用于真实的测量函数已知的情况,如算法仿真测试[8,9]和测量超精密自由曲面[7]等。因此,采用一种通用的方法来给出任意阶次多项式拟合不确定度的表示式是很有必要的。

本文提出了一种采用矩阵方程表示的任意阶次多项式最小二乘拟合的不确定度计算方法。根据这个方法,可以进一步得到测量数据的最佳拟合阶次以及拟合后积分计算的不确定度。同时,本文通过仿真进一步研究了该方法的特性,验证了其查找最佳拟合阶次的有效性。

2 原理分析

2.1 拟合系数的方差

m组测量数据的n阶多项式最小二乘拟合可以看成是求解n+1个参数的线性方程组,方程组个数为m个,一般情况下测量数据个数m大于n+1,所以,这个方程组为超定方程组,可以写为：

(1)

(2)

这个超定方程组可以由广义逆矩阵求解,写成：

(3)

式中Pinv(A)或者K都为矩阵A的广义逆矩阵。由于测量存在误差,Ys并不是对应测量点的真实结果,假设对应测量点的真实结果为Y,可以认为测量结果满足的真实的多项式关系参数为α0,…,αn。与式(3)类似,可以得到真实参数表达式：

α=Pinv(A)Y=KY

(4)

测量结果与真实结果之间的误差可以表示为：

εi=ysi-yi

(5)

式中ysi和yi分别为Ys和Y中的第i个元素。将式(3)展开并代入式(5),消掉Ys中的元素,得到：

(6)

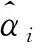
(7)

对式(7)两边同时计算方差,得到：

(8)

式(8)中,由于αi为真实的多项式关系参数,为固定值,其方差为0。同时,假设每次测量的误差是独立的且同分布的,式(8)可以化简为：

(9)

式中σ为测量值和真实值之间的标准偏差。然而,真实值在测量过程中是无法得到的,所以,这里采用拟合残差的标准偏差s来代替σ。拟合残差为测量结果与拟合后得到结果的差,对于m个测量数据点,采用n阶拟合时,得到的m个拟合残差数据的自由度为m-n-1,所以可以得到s的表达式为：

(10)

式中Δyi为拟合残差。用s来代替σ后,式(9)进一步化简为：

(11)

2.2 拟合系数的协方差矩阵

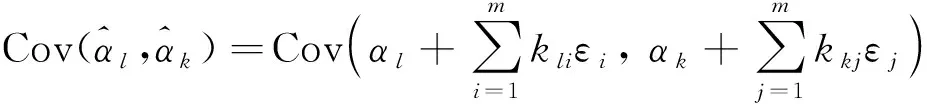
(12)

由于每次测量的误差是独立的且同分布的,可以得到误差之间的协方差为：

(13)

将式(13)代入式(12)中并采用拟合残差的标准偏差s来代替σ,式(12)可以简化为：

(14)

结合式(11)和式(14),可以得到拟合参数的协方差矩阵C可以表示为：

C=s2KTK

(15)

这里注意在计算式(15)时,需要对测量点数据进行归一化：

(16)

式中：X为由测量点x1，…，xm构成的矢量；mean(X),max(X)和min(X)分别为x1，…，xm的平均值、最大值和最小值。归一化后,可以使得矩阵A中的元素相差不大,从而使得在计算广义逆矩阵K时避免截断误差。

2.3 拟合结果的不确定度

在拟合区间内的任意点x0所对应的拟合结果y0可表示为：

(17)

根据不确定度的合成法则,y0的合成不确定度可以表示为：

u2(n,y0)=(xn0)2Var(αn)+…+(x0)2Var(α1)+

xn0xn-10Cov(αn,αn-1)+…+

x20x0Cov(α2,α1)

(18)

将式(18)改为为矩阵表达：

u2(n,y0)=X0CXT0

(19)

式中矩阵C为拟合参数的协方差矩阵,可由式(15)求得。矩阵X0为：

X0=[xn0xn-10…x01]

(20)

将式(15)代入式(19)中并开根号,就可以得到拟合结果y0的不确定度的表达式：

(21)

由式(21)可知,y0的不确定度u(y0)由3个变量决定：一是拟合残差的标准偏差s,拟合残差越小,拟合结果的不确定度越小；二是矩阵K,矩阵K由拟合阶次和测量点决定,与测量结果无关,不同的测量点和拟合阶次决定了不同的拟合不确定度；三是矩阵X0,为拟合点的位置,也就是说不同的拟合点对应的拟合不确定度不同。

2.4 最佳拟合阶次

由第2.3节可知,同一条拟合曲线上,每一个拟合点所对应的拟合不确定度都不相同。为了得到最佳的拟合阶次,就需要定义一个拟合曲线的平均拟合不确定度。在拟合区间内,等间隔的取一定数量的采样点,可以得到每个采样点所对应的拟合不确定度u(y0i)。将每个采样点看成是独立的一次测量,则可以得到采样点平均的拟合不确定度为：

(22)

式中l为采样点的个数。当采样间隔足够小时,式(22)则可以写为积分的表达式：

(23)

式中[a,b]是拟合的区间。对于不同拟合阶次所得到的拟合曲线,都可以得到一个平均的拟合不确定度。而平均拟合不确定度最小的那个曲线对应的拟合阶次,认为是最佳的拟合阶次。

2.5 拟合曲线积分结果的不确定度

在一些场合中,需要对拟合后的曲线做积分,而积分结果的不确定度同样与拟合有关。n阶多项式拟合后的积分结果可以表示为：

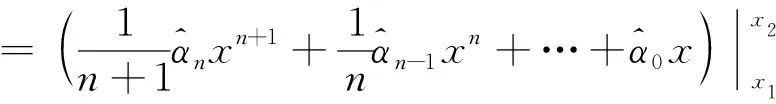
(24)

与从式(17)到式(21)的推导相类似,根据不确定度的合成法则,式(23)积分结果的不确定度可以表示为：

u2int(n,x1,x2)=X12NCNTXT12

(25)

同样,代入将式(15)代入式(25)中并开根号可以得到：

(26)

其中矩阵N和X12分别为：

(27)

(28)

3 实例仿真分析

3.1 仿真模型

假设一个实际的物理系统所满足的真实的多项式关系如下：

(29)

式(29)描述的原函数在实际测量过程中是无法得知的,这里采用这样的假设模型来对本文中描述的方法进行仿真分析。在式(29)定义的区间等间隔取样x1,…,xm各点,由式(29)可直接得到取样点所对应的真实值y1,…,ym。

在真实值上叠加一些随机的误差,模拟实际测量时的误差。随机的误差满足矩形分布,其幅值相对于测量值约为10-2量级,表示为：

(30)

式(29)中e也可以看成是测量值误差的最大值。增加误差后,测量得到的值可以表示为：

ysi=yi+rand(2e)-e

(31)

其中rand(2e)表示从0到2e之间产生矩形分布的随机数。所以,由式(31)产生的测量值ysi是从yi-e到ysi+e之间分布的,其标准测量不确定度为：

(32)

3.2 拟合不确定度计算

由式(21)可得到每个点的拟合不确定度。将式(21)看成是2部分的乘积,一部分是s,可由式(10)计算；另一部分写成t,表示为：

(33)

s只与测量的结果和拟合的结果有关,所以这里将其称为y轴相关量；t只与采样的点和计算点位置有关,这里将其称为x轴相关量。y轴相关量反应了测量结果和拟合结果之间的偏差对不确定度的影响。x轴相关量反应了不同拟合阶次和拟合点位置对不确定度的影响。下面分别对这2部分进行计算和分析。

在仿真计算中,一共模拟产生了21个测量数据,分别进行了从1阶到18阶拟合。其中,y轴相关量的计算结果如图1所示,总体上,随拟合阶次升高,y轴相关量减小。图1中的放大示图可以看出,从10阶到12阶拟合,以及从13阶到16阶拟合出现的小幅度的上升,由式(10)可知,这是由于自由度的减小造成的。当采用13阶拟合时,y轴相关量的值最小,与实际的原函数为5阶相差较大。

图1 仿真得到的y轴相关量与拟合阶次的关系Fig.1 The relationship between y-related part of fitting uncertainty and fitting order in this simulation

x轴相关量t的计算结果如图2所示,对图2中得到的不同拟合阶次下的t求平均值就可以得到如图3所示的曲线。

图2 不同拟合阶次下的拟合曲线Fig.2 The fitted value with respect to different fitting order

图3 x轴相关量tave随拟合阶次的变化Fig.3 The average of x-related part tave with respect to the fitting order

(34)

式(34)实际上就是式(22)除以s得到的结果。由图2和图3可以得到如下3个结论：1) 在拟合曲线的中间部分,x轴相关量较小,而在拟合曲线的两头,x轴相关量变大；2) 随着拟合阶次的增加,tave单调增加。在11阶以下时,tave基本为线性增加,当超过12阶时,tave急速增加,这也是为什么一般不选取高阶多项式拟合的原因。3) 随着拟合阶次的增加,x轴相关量在拟合区间两边增加的速度远大于中间区域。从图2中可以看出,5阶到15阶的拟合曲线都与实际测量点符合的很好,但是到了18阶的时候,在最右端出现了比较大的波动,这就是所谓的龙格现象[11],在该位置,x轴相关量也相应的出现了极大值。

s与tave的乘积就可以得到由式(23)所定义的曲线的平均拟合不确定度,再除以测量数据的平均值,就可以得到相对的拟合不确定度。图4显示了拟合曲线的相对平均不确定度随拟合阶次的变化。在低阶的拟合阶段,相对平均不确定随拟合阶次的增加快速减小,主要是因为s随拟合阶次1阶到5阶快速从5.1×10-1快速减小到了2.3×10-3,而tave再线性地缓慢增加。拟合阶次从5阶到15阶变化时,s减小的速度变缓,tave增加的速度超过了s减小的速度,使得整体的曲线随拟合阶次缓慢增加,从而形成了一个极小值点。当拟合阶次进一步增加时,tave增加的速度大大提升,从而使得整体的拟合不确定度快速增加。所以,在这个仿真模型中,通过本文的计算方法,最终得到的最佳拟合阶次为5阶,与假设的原函数阶次相同,拟合的平均不确定度为2.3×10-3。同时也可以看出,拟合的平均不确定度是小于测量的不确定度的,所以说通过最小二乘拟合,是可以一定程度上减小测量引入的不确定度的。

图4 拟合相对不确定度随拟合阶次的变化Fig.4 Relative uncertainty with respect to the fitting order

4 结 论

在多项式最小二乘拟合中,每一点的拟合不确定度都是不同的。中间点的拟合不确定度要远小于两边的拟合不确定度。同时,测量的不确定和测量点会影响到曲线的拟合不确定度。曲线的拟合不确定度可以看成是x轴相关量t和y轴相关量s的乘积。当拟合阶次增加时,由于拟合残差降低,s减小,然而t会增加,所以存在不确定度最小的拟合阶次,为最佳拟合阶次。