基于约瑟夫森量子电压的谐波电压测量方法研究

徐熙彤， 贾正森， 王 磊， 周天地， 潘仙林， 石照民

(中国计量科学研究院 电磁计量科学技术研究所，北京 100029)

1 引 言

近几十年来，随着量子物理和电磁精密测量的发展，以及约瑟夫森效应[1]的发现，建立量子基准成为国内外电磁计量领域研究的热点[2，3]。美国国家标准与技术研究院(NIST)、德国联邦物理技术研究院(PTB)和日本产业技术综合研究所(AIST)[4]基于约瑟夫森效应成功研制了约瑟夫森结，在特定的微波频率下可以产生具有量子精度的微小电压;在此基础上，将约瑟夫森结串联后可以输出最高10 V的电压，不同数量的约瑟夫森结连接组合在一起，可以产生从0到10 V具有量子准确性的任意电压，即可编程约瑟夫森电压基准(programmable Josephson voltage standard, PJVS)[5]。

各国计量院已经将可编程约瑟夫森电压基准应用于正弦功率的测量[6]。PTB将约瑟夫森电压基准应用于电流及电阻阻值的测量[7,8]；NIST通过产生两路独立的PJVS电压，实现对两路信号的同时测量，解决了由于分时所引起的测量误差，可以应用于交流量子功率的测量[9]；AIST采用差分采样测量技术，使用感应分压器(IVD)和10 V PJVS芯片，测量了有效值为20 V的正弦波，扩大了该技术的电压应用范围[10,11]。

目前，中国计量科学研究院(NIM)已经研制了交流量子电压驱动系统[12]，并使用该系统驱动约瑟夫森结阵产生阶梯波信号。在阶梯波的输出过程中，由于过渡过程和吉布斯现象，首先应对数据进行筛选，采用先离散傅里叶变换(DFT)再平均的方法，或者片段采样的方法[13，14]；在此基础上，通过换向差分采样对基波功率进行测量，实现了基波功率向量子基准的过渡[13]。

为了规范谐波检测仪器，提高电网谐波检测的准确性，保证国家量值溯源的统一性，NIM于2006年建立了工频谐波标准，该测量装置采用全波形采样方法。为此，本文基于PJVS研究谐波电压测量方法，从而将谐波电压与量子电压建立联系，实现谐波电压向基本物理常数的溯源；同时，提出一种加权傅里叶变换的方法，该方法可以在任意去除不理想采样点的情况下，最大化地保证重构谐波电压信号的有效数据，从而提高电压幅值和相位测量的准确度。

2 加权傅里叶变换

2.1 矩阵形式的傅里叶变换

假设周期谐波信号y表示为：

(1)

式中：a0为直流分量；ai、bi为i次谐波分量；ω为基波角频率；K为最高谐波次数；t为时间。

通过将连续信号离散化，式(1)转化为矩阵形式，令t=t0,t1,…,tN-1，p个周期的连续信号离散为N维信号向量：

Y=CT

(2)

式中：Y=[y0,y1,…,yN-1]，为离散得到的信号向量；C=[a0,a1,b1,a2,b2,…,aK,bK]，为周期谐波信号的直流及各次谐波分量；矩阵T为时间离散矩阵：

对得到的N维信号向量进行离散傅里叶变换，可以恢复得到周期信号内所包含的各次谐波分量：

C=YF

(3)

式中F为离散傅里叶变换系数矩阵

将式(2)代入式(3)，则TF=E。离散傅里叶变换系数矩阵F是时间离散矩阵T的右伪逆矩阵，时间离散矩阵T是离散傅里叶变换系数矩阵F的左伪逆矩阵。若要通过信号向量Y计算该信号的各谐波分量，可使用离散傅里叶变换系数矩阵F，或者时间离散矩阵的伪逆矩阵T+。

虽然时间离散矩阵T的行数与列数不相等，但是时间离散矩阵T为列满秩矩阵，因此存在唯一的右伪逆矩阵，且可通过式(4)计算得到：

T+=(TTT)-1TT

(4)

2.2 差分采样

在使用PJVS对周期谐波信号进行测量时，常采用差分采样的方法。根据被测信号产生相应的阶梯波信号，利用PJVS输出的具有量子精度的阶梯波信号，与被测信号进行差分，对差分得到的小信号进行采样。

在对周期谐波信号进行测量时，与测量正弦信号相同，首先通过理论计算，得到阶梯波信号的台阶值。假设阶梯波信号有M个台阶，每个台阶上有L个数据点，通过计算，可以得到每个台阶的电压值：

(5)

为了实现测量误差衰减的最大化，通过调节被测信号和阶梯波信号的相位，使采样时的差分信号尽可能小。当被测信号和阶梯波信号的相位相等时，得到的差分信号最小，测量误差最小，即被测信号与阶梯波信号相交于台阶中点，如图1所示。

图1 调相后的差分信号Fig.1 Differential signal after phase modulation

采样得到的差分信号加上相应的量子电压台阶值，即为被测信号的瞬时数据:

ym,l=sm,l+dm,l

(6)

式中：dm,l为差分信号的采样数据；ym,l为恢复得到的被测信号瞬时数据。

2.3 加权傅里叶变换

在使用交流量子电压驱动系统驱动PJVS产生阶梯波信号进行电压测量时，由于过渡过程和吉布斯现象，使得处于台阶前端的数据存在较大偏差，在后续计算中会引入误差。加权傅里叶变换首先对采样数据加权，将处于过渡过程的数据权重置零，即：

(7)

式中：P=diag(ρj), 为权重矩阵;j=0,1,2,…,N-1;ρj=0或1，或者在能够准确判断数据的重要性时，权重也可以为其他值。

对加权后的信号进行离散傅里叶变换，得到加权信号的傅里叶变换系数：

(8)

由式(2)、式(7)和式(8)推导,可以得到周期信号的实际谐波分量与数据加权后信号计算得到的谐波分量之间的关系：

(9)

对式(9)进行变换，得到加权傅里叶变换系数修正公式：

(10)

令D=TPF，则D为(2K+1)×(2K+1)维矩阵。由于时间离散矩阵T是列满秩矩阵，离散傅里叶变换矩阵F是行满秩矩阵。当rank(P)≥2K+1时，即至少保留2K+1个采样数据点，rank(D)=2K+1 为满秩矩阵，且行数等于列数，存在唯一的逆矩阵。使用修正矩阵D修正周期信号谐波分量，得到的修正结果矩阵是唯一的，该方法在理论上不存在偏差。所以，如果要恢复得到最高次谐波，则至少保留2K+1个采样数据。该约束条件，也符合奈奎斯特定理，即当采样频率大于信号中最高频率的2倍时，采样之后的数字信号完整地保留了原始信号中的信息[15]。

通过傅里叶变换得到的参数与实际参数之间存在线性关系，与时间离散矩阵T、权重矩阵P、离散傅里叶变换矩阵F有关。矩阵T为信号采样时的实际离散情况；矩阵P为数据的加权方式，是通过对采样数据进行分析筛选后确定的权重矩阵；矩阵F为离散傅里叶变换矩阵，仅与进行傅里叶变换的数据个数有关。

先DFT再平均的方法，在数据处理时，为了不影响相位的恢复，必须同时去掉处于台阶前端和后端的采样数据，在采样数据的处理过程中，产生了不必要的损失。该方法能恢复的最高谐波次数与台阶数相关，即台阶数应大于最高谐波次数的2倍;然而由于过渡过程的存在，台阶数的个数增多是有限的。

于是，采用加权傅里叶变换的方法对信号幅值及相位进行计算，在不增加台阶数的前提下，大大提高了可恢复的最高谐波次数；同时，不再局限于同时去除处于台阶前端和后端的数据，不会影响相位的恢复。对于数据的处理方式更灵活，可以实现将任意数据权重置零，计算得到准确的谐波幅值及相位。

3 模拟仿真

3.1 等间隔离散

对加权傅里叶变换算法，进行仿真演示，假设1个周期谐波信号包含表1中所示谐波。

表1 周期谐波信号参数Tab.1 Periodic harmonic signal parameters

对信号进行等间隔离散，将1个周期的信号离散为等间隔的120个区间,如图2所示；对120个数据进行加权，将部分位置的数据权重置零，如式(11)所示，即将位于i=(5，12，28，36，42，61，88，90，103，115)位置的数据权重置零；然后对信号进行加权傅里叶变换，修正前与修正后的信号幅值及相位如表2所示。

(11)

图2 周期谐波信号Fig.2 Periodic harmonic signal

表2 加权傅里叶模拟仿真结果Tab.2 Weighted Fourier simulation results

通过对比修正前与修正后的幅值及相位，可以发现在对数据加权后，计算得到的谐波信号失真；但是经修正矩阵修正后，可以重构得到准确的周期谐波信号幅值及相位。因此，经仿真实验验证，该方法可以解决由于加权方式的不同，引起的信号扭曲问题。

3.2 非整周期离散

同样选择表1中所包含的各次谐波信号。将1个周期的谐波信号离散为等间隔的120.3个区间，对120个离散数据进行加权，依旧使用式(11)的加权方式。

修正前与修正后的信号幅值和相位如表2所示。结果显示，修正矩阵可以同时解决非整周期以及加权所引起的信号失真问题。

4 实 验

使用交流量子电压驱动系统和PJVS测量谐波电压，采用差分采样和加权傅里叶变换的方法计算谐波信号的幅值和相位。交流功率源选择FLUKE 6105 A，可以产生最高包含100次谐波的信号。实验步骤为：

(1) 由FLUKE 6105 A功率源作为信号源，产生含有指定基波及谐波成分的被测信号；

(2) 使用交流量子电压驱动系统驱动PJVS产生相应的阶梯波信号；

(3) 在信号调相后，被测信号输入正输入端，阶梯波信号输入负输入端，采样差分信号；

(4) 将采样得到的差分信号，加上相应的量子电压台阶值，计算被测信号的瞬时数据；

(5) 对信号瞬时数据进行加权傅里叶变换，并修正，得到信号的基波及所含谐波的幅值、相位；

(6) 换向操作，将被测信号输入负输入端，阶梯波信号输入正输入端，重复上述步骤3、4、5，对换向前后得到的结果进行平均。

4.1 实验结果

使用表1中的信号参数进行实验，电压基波有效值1 V。信号基波频率62.5 Hz，采样频率 625 kHz，即每个周期的采样点数为10 000。阶梯波为40个台阶，频率2.5 kHz，每个台阶上的采样点数为250。图3为实测差分信号，经过实测分析，根据3σ准则，将处于每个台阶前端的15个采样数据权重置零，恢复得到的信号幅值和相位结果见表3。表中，幅值相对误差为绝对误差与该谐波设定幅值的比值；在计算相位误差时，谐波相位为各谐波与基波的相位差。

图3 实测差分信号(阶梯波台阶数=40)Fig.3 Measured differential signal (step-wave steps=40)

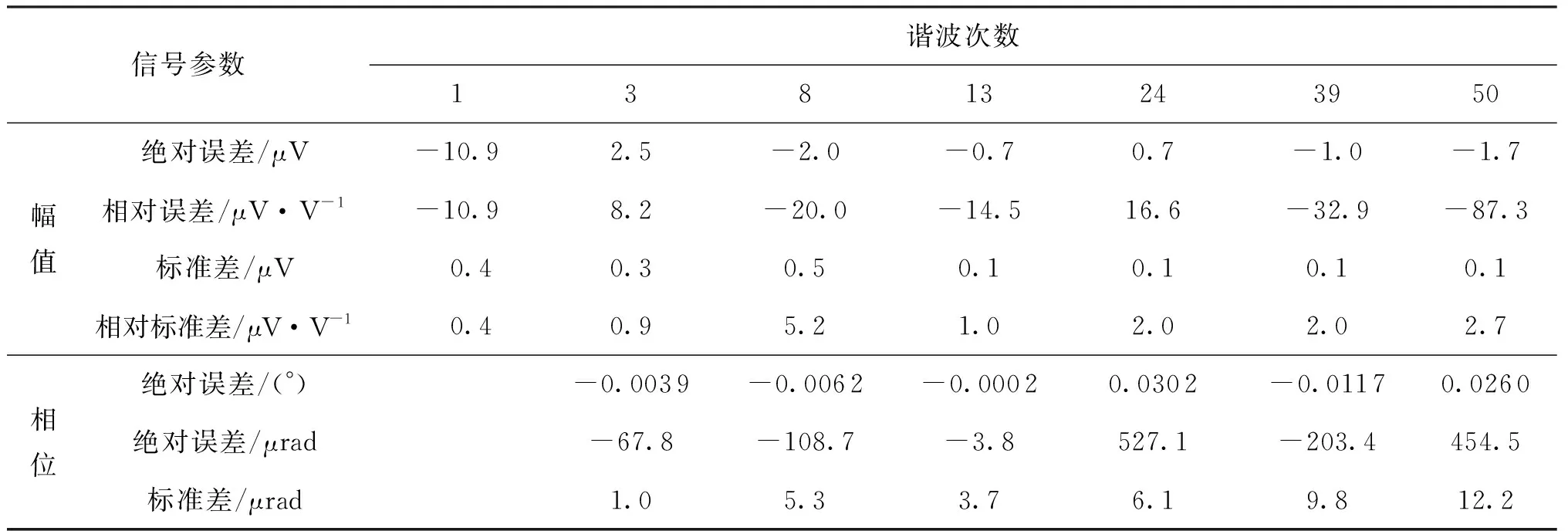
表3 实验结果Tab.3 Experimental results

4.2 结果分析

使用FLUKE 6105 A电流输出通道输出1 V电压的年稳定性(±5 ℃)为±116 μV; 电流转电压输出通道相位频率16～69 Hz时，年稳定性(±5 ℃)为±0.005°;180～450 Hz时为±0.025°;450～850 Hz 时为±0.043°;850 Hz～3 kHz时为±0.150°;3～6 kHz 时为±0.300°。

各谐波信号幅值误差均小于FLUKE 6105 A技术指标给出的电压幅值输出误差范围。相位误差也均小于FLUKE 6105 A技术指标给出的电压相位输出误差范围，使用加权傅里叶变换的方法计算得到的谐波信号幅值及相位具有可靠性。

从实测实验数据中可以看出，谐波电压幅值和相位测量的结果比较理想。幅值测量标准差均小于1 μV,其中8次谐波的幅值测量标准差最大，为 0.5 μV;相位测量标准差均小于15 μrad，其中50次谐波的相位测量标准差最大，为12.2 μrad。

表3中的实验结果验证了将可编程约瑟夫森电压基准应用于谐波电压测量的可行性。通过约瑟夫森量子电压测量谐波信号，在FLUKE 6105 A功率源输出的误差波动范围内，结果可靠；并且，测量结果的标准偏差较小，说明该测量系统的稳定性较好。

在此基础上，根据文献[14，16～19]推想，可以对差分信号限幅。根据周期谐波信号所包含的谐波分量，对差分信号进行分析,除了将处于过渡过程的数据权重设定为零以外，将差分信号幅值超出限值的数据权重同样置零；或者通过增多阶梯波信号的台阶数，提高阶梯波信号对被测信号的复现度，降低差分信号的幅值大小。

同时，在将可编程约瑟夫森电压基准应用于谐波测量时，不同于基波测量，高次谐波的频率较大，由于直接数字式频率合成器(DDS)位数有限，阶梯波信号频率与被测信号频率并不能完全一致，因此信号在高次谐波时会发生相对移动，影响相位的恢复效果。

上述限幅和非整周期修正的想法，为进一步提高谐波测量的精密度，更深入地研究基于约瑟夫森量子电压的谐波电压精密测量提供了方向与思路。

5 结 论

本文通过实验验证了将可编程约瑟夫森电压基准应用于谐波电压测量的可行性。使用可编程约瑟夫森电压基准输出的阶梯波作为参考，实现了对谐波电压的精密测量。

为了解决量子电压测量中必须规则去除采样数据点的算法问题，提出了一种加权傅里叶变换的周期谐波信号计算方法。通过理论推导、模拟仿真以及实验验证，表明所提出的加权傅里叶变换方法是正确且有效的；该方法在任意去除采样数据点后仍能准确重构谐波信号，能够充分利用采样信息，对数据的处理方式选择更加多样化。在分析实验结果的基础上，提出了进一步提高谐波精密测量的研究方向。