基本电荷量常数定值综述

刘 民, 彭 明

(北京东方计量测试研究所，北京 100086)

1 引 言

2018年11月16日第26届国际计量大会(Conference Generale des Poids et Mesures, CGPM)表决通过了新的国际单位制(SI),于2019年5月20日正式启用了新SI。其1号决议定义了“基本电荷量e为1.602 176 634×10-19C”,其中库仑C=A·s, 电流单位安培A和时间单位秒s是SI基本单位。在1号决议的附录2中提到“真空磁导率μ0,在一定的相对标准不确定度范围内等于4 π ×10-7H·m-1,该不确定度等于本决议通过的精细结构常数α推荐的不确定度,即2.3×10-10；且未来真空磁导率的数值将通过实验确定”。在1号决议附录3中电流单位重新定义“安培,符号A,SI的电流单位。当基本电荷量e以单位C,即A·s表示时,将其固定数值取为1.602 176 634×10-19C来定义安培,其中秒用ΔνCs定义”。

新的国际单位制SI确定了基本电荷量e是一个没有不确定度的基本物理常数,同时把真空磁导率μ0由原来的固定数值变为了具有不确定度的待测数值。电流安培作为SI基本单位的地位没有改变,只是用基本电荷量来重新定义安培。那么基本电荷量的精确数值是如何确定下来的呢？本文将从电磁学单位制的内在逻辑来说明基本电荷量是计算出来的,而不是精确测定的。

2 电磁学单位制简介

国际单位制SI诞生于1960年第11届CGPM,选择的6个基本SI单位的原则是：所选单位是每个学科领域有代表性的,且能够推导出其它物理量单位的基本单位,它们之间尽量独立不相关。长度单位m,质量单位kg,时间单位s,电流单位A,热力学温度单位K和发光强度单位cd,成为首批确定下来的国际单位制的基本单位[1]。1971年，新增加了物质的量单位mol，共7个构成SI基本单位。电磁学的其它单位,如电压单位V、电阻单位Ω、电容单位F、电感单位H等都属于21个具有专门名称的SI导出单位。

依据能量守恒原理,让电磁力做功等价于机械力做功,或电磁功率等价于机械功率,是确定电学基本单位的原则。库仑定律和安培定律揭示了电与力之间的关系。

库仑定律：

(1)

式中：F是两个点电荷之间的力；r是点电荷距离；q1和q2是点电荷的电荷量。ke是库仑定律公式系数,在绝对静电单位制(CGSE)中ke=1是无量纲量；在国际单位制(SI)中ke=4 π ε0,ε0为真空介电常数,单位F/m。

安培定律：

(2)

式中：F是两条闭合导线c1、c2之间作用力；dl1和dl2是导线上微分线原；r21是线原距离；I1和I2是两导线上的电流；er21是单位矢量。km是安培定律公式系数,在绝对电磁单位制(CGSM)中km=1是无量纲量；在国际单位制(SI)中km=μ0/4 π ,μ0为真空磁导率常数,单位H/m。

在SI单位制诞生之前,电磁学没有自己独立的单位体系,仅依赖于长度、质量和时间量纲,有基于库仑定律的绝对静电单位制CGSE,有基于安培定律的绝对电磁单位制CGSM,还有混合两种单位制的高斯单位制CGS,统称为绝对单位制。1901年意大利GroigiG提出了MKSA(米、千克、秒、安培)单位制,也称为实用单位制[2],电磁学独立的单位体系由此诞生。在1904～1910年的一系列电磁学国际会议上确定了两个电学基本量,电流和电阻[3]： “从硝酸银溶液中以0.001 118g/s电解出银的恒定电流为1A”； “在水冰融化温度下,质量为14.452 1g、长度为106.300cm横截面恒定的水银体的电阻为1Ω”。

1946年CGPM废除了绝对单位制,采用MKSA制,仅选择了电流单位安培为基本单位。把真空磁导率确定为固定数值,依据公式(2)定义安培：“在真空中,截面积可忽略的两根相距1m的平行而无限长的圆直导线内,通以等量恒定电流,长度为1m的导线间相互作用力为2×10-7N时,则导线中的电流为1A”。安培定义的意义在于规定电磁力与机械力等效,是安培定律特例化的描述。定义文字背后的含义是令真空磁导率μ0成为固定的有量纲的无理数,即μ0=4 π ×10-7H/m,其量纲的作用可以使电磁学单位体系从机械力学单位体系中独立出来。

基于安培定律原理的电流天平,在计量应用中广泛用于比较砝码质量,而不能绝对复现安培的单位量值。实际上,用欧姆定律I=U/R来测量电流,然而电压单位伏特V和电阻单位欧姆Ω,却不是SI基本单位,这是原SI单位制长期困扰电磁学溯源的基本问题。

在电学计量体系中,实物电压基准有两种：饱和惠斯顿电池的1.018 V化学电动势基准，齐纳二极管的1 V、10 V固态电压基准；其中1.018 V基准年稳定性可达6×10-7。实物电阻基准在1 Ω定值,是锰铜合金丝在骨架上缠绕的四端子标准电阻,年稳定性可达1×10-7。因为电流和电荷量都不能长期稳定保存,所以电磁学计量中没有电流和电荷量的实物基准。

既然安培能作为机械功率与电磁功率的桥梁,选择适当的系数能让Fv=UI(v是速度,U是电压),等式两边有最简单的形式,那么能否也可让基于库仑定律的电荷量成为机械力和电磁力的桥梁呢？为什么没有出现电荷量计量标准呢？确定哪个单位是基本单位的唯一条件是“机械功率和电磁功率都能用瓦特来测量”[2]。电荷量和电流都有相应电磁定律与力学单位相关，然而电荷量的测量非常困难,有关电荷量测量装置很少,稳定性也不高；而电流参数已经在20世纪初的第二次工业革命中广泛应用,是功率测量的关键参数,所以电流单位安培成为基本单位是当时实用单位制的最佳选择。

3 密立根油滴实验测定电荷量

1897年汤姆森在阴极射线实验中,发现电子并测出了电子的荷质比。1911～1913年密立根巧妙地利用油滴在重力场中下落和静电场中上升的过程,测算得出电荷量是量化的,并且给出了精确的电子电荷量值,用绝对静电单位制表示为e=(4.744±0.009)×10-10esu(1 esu = 3.3356×10-10C),测量不确定度0.2%,实验装置如图1[4]。为了防止空气对流,测量腔体全部浸入到恒温液体中；用气泵控制和水银气压表监测腔内气压,用于调节空气黏度，光学装置观测油滴的运动时间,X射线灯改变油滴的电荷量。

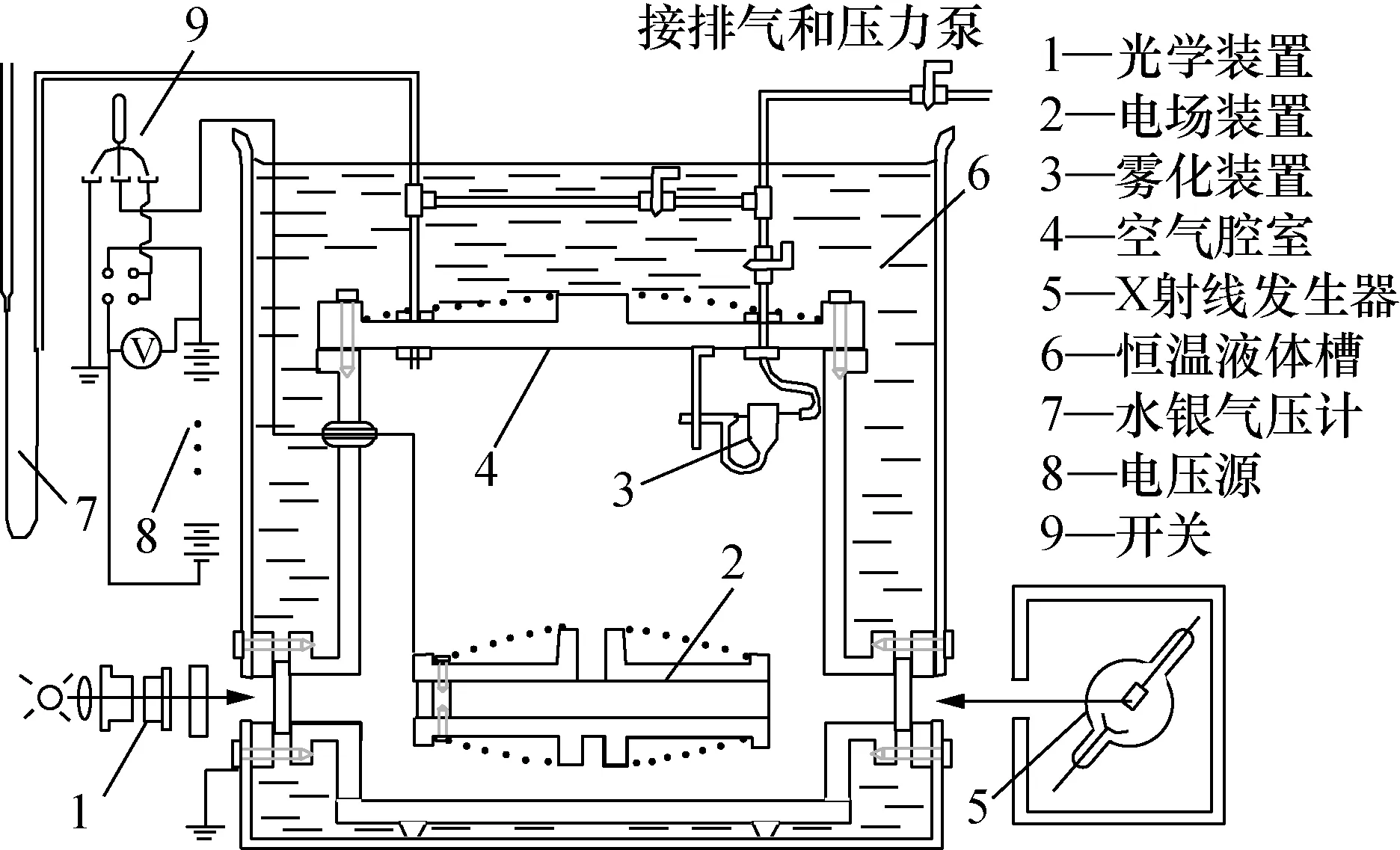
图1 密立根油滴实验装置Fig.1 Apparatuses of Millikan’s oil-drop experiment

不施加电场时,细小的油滴在空气浮力、空气黏度和重力的作用下匀速向下运动；施加电场时,则匀速向上运动,行程约5 mm。测量油滴穿越2条间隔1.5 mm光学刻线的来回时间和电压值,计算出油滴的电荷量。X射线照射后，油滴上的电荷发生变化,则变化的电荷量总是基本电荷量的整数倍。

现在密立根实验不作为测定基本电荷量数值的依据,在大学物理实验中是经典的实验课程,该实验的意义在于证实了基本电荷量是不可细分的,是量子化的[5]。密立根实验测定的电荷量准确度尚不能达到计量标准的要求,其它确定电荷量的实验没有出现,因此至今没有出现电荷量的量值溯源体系。

4 电学量子基准

约瑟夫森电压标准是复现电压量值的自然基准。在超导体-绝缘膜-超导体组成的约瑟夫森结上,当绝缘膜厚度小于10-8m时,两边超导体中的电子气会出现相互的弱耦合[6],在图2(a)的两个超导体之间施加电压V时,绝缘膜(也称为结)的地方辐射出E=2eV能量的电磁波量子E=h(nf1),e是基本电荷量,h是普朗克常数,f1是电磁波频率,n=1,2,3,…是谐波次数；反之,两超导体被照射频率为f1的电磁波时,2eV的能量被结吸收,eV也是能量的单位,在绝缘膜两边出现电压,图2(b)中把m个结串联起来可输出更高的电压V。于是电压与电磁波频率之间存在量子化的联系,频率溯源到原子频标的不确定度很容易达到10-12,约瑟夫森电压比对不确定度可达10-8量级。

约瑟夫森电压标准：

(3)

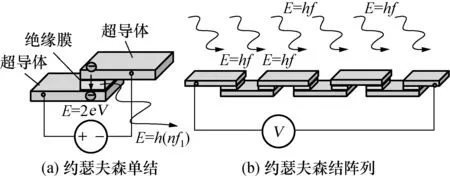
图2 约瑟夫森结上的电压和电磁波频率Fig.2 The voltage and frequency of microwave on Josephson junctions

量子化霍尔电阻是复现电阻量值的自然基准。半导体异质结的材料界面上,在低温(1.2 K)条件下会出现二维电子气,见图3。自由电子的空间分布被称为电子气,在二维x-y面法线方向上施加磁场B,x方向运动的电子受洛仑兹力作用,偏向y方向,产生霍尔效应电压Vxy,y方向的霍尔电压与x方向的电流之比称为霍尔电阻RH=Vxy/I。霍尔电阻随磁场增大而增大,当磁场增大到4 T以上时,磁场强度使二维面的载流子浓度出现量化特征,即RH不跟随磁场的变化而变化,表现为平台,在磁场增加过程中有多个平台i=1,2,3,…。平台出现时x方向的电压接近为零,Vxx≈0。RH只有固定的几个量值,用低温电流比较仪电桥进行比例变换,可以传递更宽的电阻范围,测量不确定度可达10-9量级。

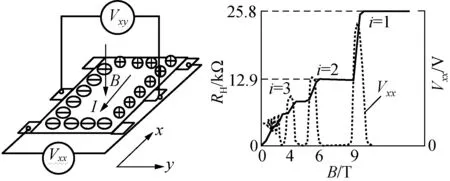
图3 量子化霍尔电阻原理示意图Fig.3 Principle of quantum Hall Resistance

量子化霍尔电阻标准：

(4)

式中：RH为霍尔电阻,Ω；h为普朗克常数, J·s；e为基本电荷量,C；i为自然数。

单电子隧道泵可复现电流量值在100 pA范围内,不确定度达到10-7量级[7]。当电容器金属极板和绝缘介质的尺寸小到纳米量级时,绝缘介质两边电子气的波函数会发生相位相干作用,在电容器施加一定电压时,电子越过绝缘势垒的阻塞,从一边隧穿到另一边,在温度极低(mK量级)条件下,隧穿的电子将一个一个地通过绝缘介质,驱动电压的频率f2能控制流过电容的电流I。电流定义为单位时间通过的电荷量,电子电荷量为e,则单电子隧道泵能够实现电流安培的量值复现：

I=ef2

(5)

用功率天平测定普朗克常数h时,使用了约瑟夫森电压标准和量子化霍尔电阻标准；应用这两个自然基准测定普朗克常数时,基本电荷量e没有发挥作用,电功率公式中,电荷量e做为分子和分母相抵消了：

(6)

式中：kV,kR为测量过程中的比例系数,无量纲。

上述3种测量装置分别把电压、电阻、电流与普朗克常数h,和基本电荷量e联系在一起,称为电学量子三角形[8]。本次SI修订之前,人们担心的是电学量子三角形能否相互验证,尤其是电流单位能否用基本电荷量来准确复现[9]。在新SI启用之后,这些问题就不存在了,电流单位安培用基本电荷量来定义,既可以用单电子隧道泵复现,也可以用量子电压和量子电阻来复现。安培不再与“无限长直导线”相关联了。

(6)

式中：kI为测量过程中的比例系数,无量纲量。

5 基本电荷量的确定

1990年国际上启用了约瑟夫森常数KJ-90和冯·克里青常数RK-90。是否能用这2个常数直接计算基本电荷量e呢？实际上,这2个常数不能直接计算获得电荷量,而是用这2个常数测定普朗克常数h,待确定了h再反过来计算e,这个过程是电磁学和机械力学之间相互联系的过程。如果用KJ-90和RK-90直接计算的基本电荷量用e′表示,则：

=1.602 176 492×10-19C

(7)

式(7)计算得到的e′与新SI定义的基本电荷量e=1.602 176 634×10-19C相差了-8.9×10-8C。可见,基本电荷量不能简单地由电学常数推算。

基本电荷量的定值是通过精细结构常数α计算出来的。精细结构常数是量子力学、量子电动力学中非常重要的常数,它是与原子结构相关的常数,α的值联系着电磁力和亚原子带电粒子,尤其决定了原子如何保持住它的电子[10]。20世纪初期Einstein、Planck、Sommerfeld等物理学家对h与e2/c具有相同的量纲(CGS单位制)很感兴趣,Sommerfeld开展了大量理论研究[11]。在早期的波尔原子模型中,电子以轨道运动存在于原子核周围,α2被推导为氢原子中电子轨道半径与电子粒子半径的比值。α也被解释为氢轨道电子速度与光速的比值,轨道角动能的量化值由3变到2 时,氢原子发射在656.3 nm处的成对的红光谱线,被称作精细结构谱线,精细结构常数也因此命名。薛定谔的物质波理论取代波尔原子模型后,精细结构常数被保留下来,被看作自然界耦合常数之一,用牛顿力学中的万有引力常数G来类比,精细结构常数α可理解为描述所有带电粒子电磁相互作用强度的参数。精细结构常数α的表达式由普朗克常数h,真空光速c,基本电荷量e和真空磁导率μ0组成:

(8)

式中ε0μ0=c-2。

测定α的方法有量子化霍尔电阻效应、交流约瑟夫森效应、中子的德布罗意波长、μ粒子超精细结构、铯原子D1线的绝对光频和电子磁动量等几种方法[12]；这些方法的测量不确定度均达到了10-8量级，其中电子磁动量法的测量不确定达到了2.5×1010[13]。习惯上用α的倒数α-1来表示精细结构常数的值,2017年科学技术数据委员会CODATA推荐值为：

α-1=137.035 999 173(35)

假设真空磁导率μ0仍为4 π ×10-7H/m,让c,h成为SI定义的固定值,计算基本电荷常数e：

这就是新SI定义的基本电荷量常数,最后两位“92”进位截断,使用中作为没有不确定度的数值。在式(8)中，把c,h,e作为SI固定值,没有不确定度；那么,只能让μ0为待测值,当精细结构α有最新的测定值后,μ0的值也将重新更新,不再是纯无理数4 π ×10-7,测量不确定度跟随α的测量结果而定[14],SI定义中推荐为2.3×10-10。

电荷量的概念可追溯到库仑扭力秤实验。汤姆森阴极射线发现了电子,密立根油滴实验证实了电子电荷量是量化的,初步测定了电子电荷量。功率天平利用约瑟夫森常数KJ-90和冯·克里青常数Rk-90测定了普朗克常数h。

一旦普朗克常数h被认为是没有不确定度的固定值后,再利用精细结构常数α公式,就可以确定基本电荷量e的数值。在精细结构的表达式中,把真空磁导率μ0与基本电荷量e的角色互换一下,让μ0作为待测参数,让e成为固定数值,最后重新计算约瑟夫森常数和冯·克里青常数,去掉下角标的“-90”,变成了固定数值KJ和Rk。这就是电磁学常数们在新国际单位制SI中的发展脉络,见图4。

图4 电磁学单位制与基本电荷量定值的发展脉络Fig.4 Development skeleton of electromagnetic unit systems and defining the value of elementary charge e

6 结 语

回顾有关电荷量的历史,理清测量电荷量的发展脉络,有助于深刻理解新的国际单位制SI变革的意义。电磁学计量的根基从实物基准发展到量子基准,电磁学单位体系仍是独立的体系,电磁学与力学之间的桥梁,从电流单位[安培]转换成真空磁导率,电与力之间更深层次的联系在于精细结构的本质,有待物理学继续发展来揭示其中的奥秘。