基于指数损失间隔的多标记特征选择算法

2020-04-30李雨婷

计算机技术与发展 2020年4期

李雨婷

(南京邮电大学计算机学院、软件学院、网络空间安全学院，江苏南京 210023)

0 引言

多标记学习的概念来源于文档分类[1-2]过程中遇到的多语义问题，经过了十几年的发展，多标记学习也慢慢成为了国际机器学习领域的热点话题。多标记学习的研究成果也在实际问题中得到了较好的应用，逐渐在图像分割[3]、图像标注[4]、面部表情识别[5]、动作识别[6]、广告推荐[7]、文本分类和生物信息学[8]等领域扮演重要的角色。

在机器学习领域，机器学习问题通常可分为监督学习、无监督学习[9]。在传统的监督学习中，每个样本与一个标记相关，而在多标记学习中一个样本可以有多个标记。且标记之间存在一定的关联性，如何提取和利用标记间的关联性成为提高多标记学习算法性能的关键。为此，可采用基于指数损失间隔的多标记特征选择算法进行特征选择，该算法不仅不依赖于具体的转换策略或分类算法，也可以有效地利用标记间的关联信息。

文中首先介绍了多标记学习和特征选择算法，以及一种多标记数据样本相似性的度量方法；然后提出一种基于指数损失间隔的多标记特征选择算法。该算法可使用样本标记的关联性使特征空间与标记空间的信息结合在一起，可得到标记间的关联信息，也独立于特定的分类算法或转换策略；最后通过现实世界数据集上的相关实验及结果对算法进行验证。

1 相关工作

1.1 多标记学习

目前，根据多标记学习算法是否利用标签之间的相关性，可以分为三个阶次：常见的一阶算法，如binary relevance，将候选标记个数为Q个的多标记问题转变成为Q个独立的二分类问题，再对每个二分类问题独立求解。calibrated label ranking[4]是一种二阶算法；此外，分类器链(classifier chain，CC)[10]算法属于高阶算法，也可用来处理多标记问题。

1.2 特征选择

特征选择[11-12]是一种数据预处理技术，常用于去除数据中的噪音和冗余特征。相比其他的降维方法，特征选择不改变数据的原有特征，使原始的数据特征被保留。

通常将特征选择方法分为3种模型：封装器模型、过滤器模型和嵌入式模型[13-14]。常用过滤器模型的特征选择方法有ReliefF[15]、Fisher Score[16]算法等。这种特征选择模型，独立于具体的分类器，所以当选择不同的分类器时也不会对算法的结果产生影响，因此被广泛应用。封装器模型直接针对给定的分类器进行优化，所以对于不同的分类学习算法，其分类性能也有不同的差异，封装器模型算法也因此受限于所选分类器的性能。而嵌入式模型算法独立于具体的分类学习算法，且其算法计算量比封装器模型小。

文中所提出的多标记特征选择算法属于过滤器模型，该算法与具体的转换策略[14]无关，可通过分类学习算法得到若干特征子空间，再根据分类性能来选择最优的特征子空间作为最终分类结果。

1.3 多标记样本的相似度

由于在多标记学习中，不同数据集的标记之间通常会有不同的关联性，这里通过构建概念结构图的方式去假设标记的结构。在传统的单标记问题中，样本间的相似度[17-18]可通过式(1)计算：

(1)

其中nl表示属于类别l的样本个数。在多标记的学习中，同一个样本有可能属于多个标记，此时不能通过式(1)明确得到两个样本所属的类别。在这里，利用式(2)[19]可以计算两个多标记样本间的相似性s(i1,i2)，其中nq为与第q个标记相关的样本个数，式(2)也可看成是Jaccard[20]的另一种表现形式。数据集中不同标记出现次数不相同，通过改变权重nq表示不同标记对样本相似度的影响。

(2)

如图1中的上半部分，表示含有ABC三种标记的结构图，图中的三角形、星形、菱形、正方形表示不同的样本，用不同的形状来描述样本在特征R1上的不同取值情况。与单标记问题不同，多标记问题中同一个样本可以同时和多个标记相关联，例如图1上半部分所示，特征R1取值为星形的样本，既与标记A相关联，又与标记B相关联。将每种标记当成一个类别，多标记问题变成了多类问题，将图1上半部分的重叠区域进行分解，如图1下半部分所示。

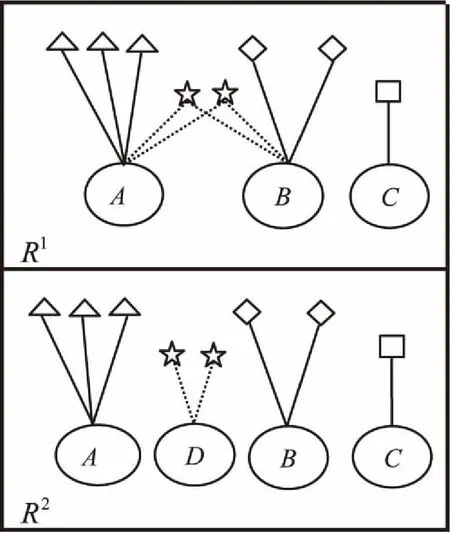
图1 多标记问题的分类

当原始问题被转换为二分类问题，如图1下半部分所示，定义了新的类别D，变成了与A和B完全不同的类别，根据式(1)可知它们之间的相似度为0，但真实的样本间相似度并不是0，因此文中所使用的方法对描述样本间相似度的关系更有效。

2 基于指数损失间隔的多标记特征选择

图2是通过式(2)来构建的简单无向图，边距越短，两个样本之间的相似度就越大。实心圆形表示样本xi，空心圆形表示与样本xi带有相同标记,且两样本间的相似度大于阈值smin的样本，七角星表示与样本xi的标记不同，且样本间相似度小于阈值smin的样本。若给出样本的相似度以及阈值smin，可在图 2的标记空间(a)中找出样本xi的近邻样本，可通过近邻样本来预测样本的标记。

图2(b)所示的是特征空间，通过特征选择可以使得样本间的距离发生变化，箭头的方向表示通过特征选择使样本间的距离发生变化的方向。图2(b)中由七角星到实心圆形的距离可能比空心圆形到实心圆形的距离更近，意味着样本在特征空间和标记空间上分布不一致。

特征空间和标记空间的样本分布不一致的特性，可能会导致样本的分类错误。如果能找到如图2(c)所示的特征子空间，使得样本(特征子空间的样本)在特征空间上的分布与标记空间上的分布一致，就可用这部分特征来寻找第i个样本的近邻，从而使分类效果更好。

特征子空间的不同会对样本间的距离产生不同的影响，从而影响损失函数值，找到合适的特征子空间，可以使损失函数最小，所以特征选择的评价准则可以选择损失函数来衡量。由此，提出了基于指数损失分类间隔的多标记特征选择算法。给定样本(xi,yi)及相似度smin，可定义：

sim(i)={(xi',yi')|s(i,i')≥smin,

1≤i'≤n且i'≠i}

(3)

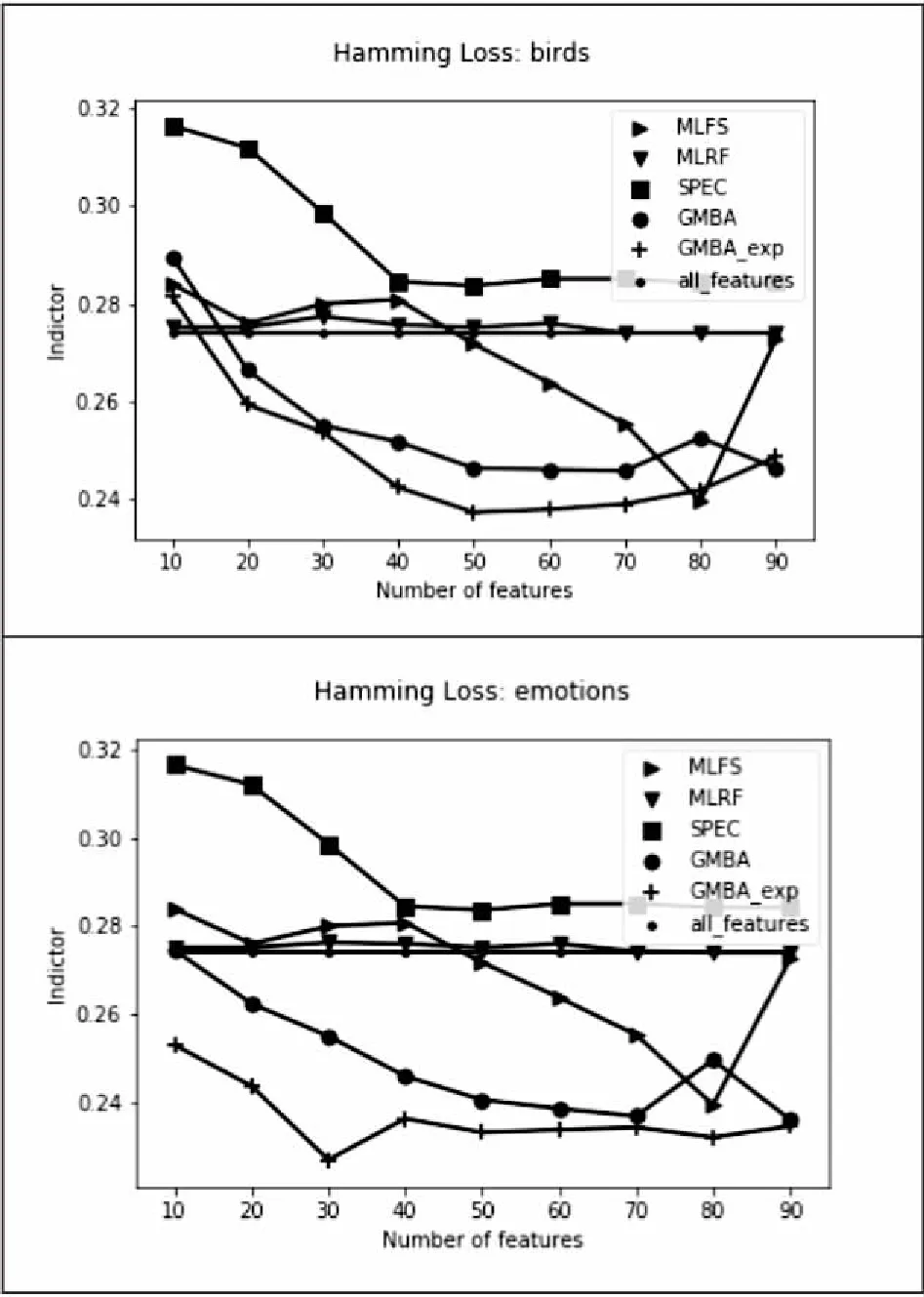
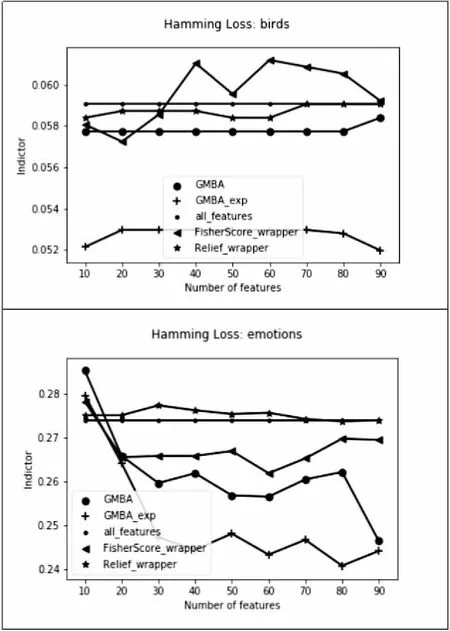
dissim(i)={(xi',yi')|s(i,i')

1≤i'≤且i'≠i}

(4)

(xi',yi')∈sim(i)

(5)

(xi',yi')∈dissim(i)

(6)

margin(i)=|‖xi-xnearhit(i)‖2-

‖xi-xnearmiss(i)‖2|

(7)

可以按照式(2)和阈值smin，对数据集进行划分，划分为与样本xi具有相同标记的样本集合sim(i)和具有不同标记的样本集合dissim(i)，通过特征空间中的欧氏距离，分别在两集合中找出与样本xi具有相同类别的最近邻nearhit(i)和不同类别的最近邻nearmiss(i)，再通过nearmiss(i)、nearhit(i)来计算分类间隔margin(i)。在此基础上，用nb(i)(near neighbor)表示xi的目标近邻样本，并定义损失函数Lossxi(w)：

(8)

损失函数的第一项表示的是惩罚与样本xi相距较远的样本，而并不是指所有的与xi具有相同标记的样本，第二项表示的是惩罚与样本xi的相距较近且与xi标记不同的样本。w为特征的权重向量，调节参数λ>0，δ(i',j)见式(9)，指数损失见式(10)：

δ(i',j)=(1-s(i,.j))·EXP(xi)

(9)

EXP(xi)=exp(max(0,margin(i)+

‖wxi-wxi'‖2-‖wxi-wxj‖2))

(10)

在这里关注的是特殊区域里被惩罚的样本且与样本xi标记不相似的样本。该区域的样本与样本xi的距离小于样本xi到其任何目标近邻的距离加上margin，对此时的样本进行惩罚。若训练集中的样本都有着损失低、分类间隔大的特点，就可以使得算法具有更好的推广性能。

图2 比较不同空间中的图

为使得损失函数最小，可优化函数式(11)，求得一组最优特征权重w*，使nb(i)中的样本到xi的距离均小于dissim(i)中的样本到样本xi的距离，使标记空间中的样本分布和特征空间一致。w*可以通过梯度下降法求得。具体见算法1。

(11)

(12)

其中，

(13)

‖xdi-xdj‖2)·(exp(margin(i)+‖xi-xi'‖2-‖xi-xj‖2))

(14)

算法1：GMBA_exp。

输入：梯度下降算法的步长βi，近邻数k，训练数据集Dtrain，阈值smin，调谐参数λ；

输出：特征权重w。

1.初始化w=1

2.fori=1 ton：

3.从训练数据中得到sim(i)，dissim(i)，

nearhit(i)，nearmiss(i)，计算margin(i)

4.依据k求nb(i)

5.ford=1 toD：

7.end

8.w=w-(βi)/‖‖，其中βi为步长

9.end

10.输出w

GMBA[19]算法与GMBA_exp算法，主要差别在于损失函数的形式上，GMBA[19]算法采用hinge损失[19]函数的形式。

3 实验

在算法的有效性验证方面，先在数据集上将SPEC(spectral feature selection)[14]、GMBA[19](运用hinge损失算法)、GMBA_exp、多标记ML_FScore(MLFS)[21]算法和ML_ReliefF(MLRF)[21]算法进行比较，MLFS、MLRF对应的是传统单标记问题中经典特征选择算法Fisher Score[16]、Relief[15]的拓展。SPEC(spectral feature selection)[14]谱特征选择，它不仅可以提取图谱信息，也可以提取类标间的结构信息。五种特征选择算法均属于过滤器模型。

3.1 数据集及参数

实验运行环境是Python 2.7，转化策略选用BR[13]，KD树、K近邻算法从Scikit-learn[22]中组成基分类器。MLRF和GMBA[19]、GMBA_exp中的近邻数均设置为3，GMBA[19]、GMBA_exp中smin和λ均设置为1，βi=0.9。从MULAN[23]上下载了四组来自不同领域的数据集，数据集的具体信息见表1。实验时，将样本方差为0的特征进行人工去除，并对数值型的特征进行归一化,所有实验结果均由10折交叉验证获得。

3.2 评价指标

在BR[13]转化策略下，将GMBA_exp与过滤器模型算法和封装器模型算法进行比较，算法性能的评价指标选[24]用F1_Macro(↑)及汉明损失(↓)，用↑表示指标值越大越好，用↓表示指标值越小越好，具体实验结果见图3～图6(由于篇幅限制，在这里只显示birds、emotions数据集的实验结果)。水平线表示不用特征选择算法时分类的结果。横轴表示所选的特征个数占特征总数的百分比，纵轴为指标值。

3.3 实验结果分析

通过两个不同的多标记评价指标，在四个多标记数据集上进行实验。实验结果显示，随着所选特征的增加，评价指标并不是单调增加或者单调减少，说明数据集中有的特征对分类性能的提高有负面影响。在多数情况下，文中提出的GMBA_exp算法相比其他算法具有更好的分类性能。此外，在与过滤器模型算法、封装器模型算法的对比实验中可以看出，在相同的BR[13]转化策略下，GMBA_exp算法的分类性能最优。

表1 数据集描述

4 结束语

实验结果表明，GMBA_exp算法优于其他算法。GMBA_exp和GMBA[19]算法都致力于寻找最优的特征子空间，使得样本在特征空间上的分布与标记空间上的分布一致，在大多数情况下，GMBA_exp算法的效果要优于GMBA[19]。综上，文中提出的基于指数损失间隔的多标记特征选择算法能更好地描述标记间的相关性，提高多标记的分类性能。

与过滤器模型算法比较的实验结果如图3和图4所示。

与封装器模型算法比较的实验结果如图5和图6所示。