无监督网络对抗生成模型的研究

王晟全，陈济颖，王奕翔，李 昂,4，李 鑫

(1.南京理工大学紫金学院，江苏 南京 210023；2.中国石油大学(华东) 储运与建筑工程学院，山东 青岛 266580；3.广西大学，广西 南宁 530003；4.南京邮电大学 通信学院，江苏 南京 210003)

0 引 言

无监督网络是比较火的一个话题，因为它将机器学习中的无监督学习领域带入了新的高度，其中的生成式对抗网络是由康奈尔大学的Goodfellow等人提出。对于它的研究，科学家们越来越感兴趣，从图1的英文文献年发文量可以看出。

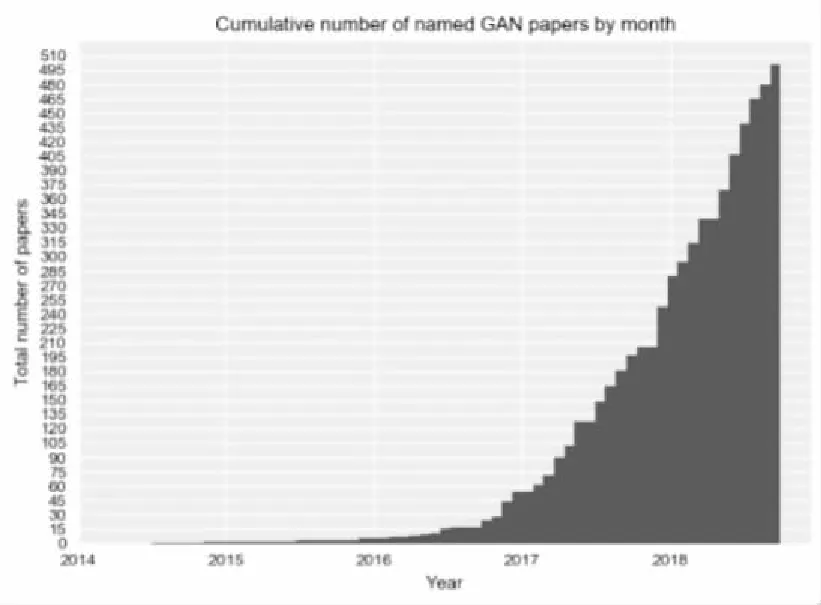
图1 Generative Adversarial Networks英文文献年发文量

对抗生成模型是基于博弈模型的，其中生成模型(Generator)必须与其对手判别模型(Discriminator)竞争。生成模型直接生成假样本，判别模型尝试区分生成器生成的样本(假样本)和训练数据中抽取的样本(真样本)。生成对抗网络(GAN)是一种生成模型，由生成器Generator和辨别器Discriminator组成。生成模型尝试了解真实数据样本的特征分布，并生成新的数据样本。判别模型是一个二分类器，判别输入是真实数据还是生成的样本。生成模型和判别模型均可以使用感知机或者深度学习模型。优化过程是极小极大博弈(minimax game)问题, 优化目标是达到纳什均衡，即直到判别模型无法识别生成模型生成的假样本是真是假[2-3]。

目前，无监督网络的大部分应用都是在计算机视觉领域。其中一些应用包括训练半监督分类器，以及从低分辨率图像中生成高分辨率图像。在科研中发现，生成模型对于整个网络训练的结果有着非常大的影响，尝试了多种改进生成式模型，有了一些改进思想。

1 相关工作

1.1 生成随机网络的简介

在研究前，先了解一下生成随机网络(generative stochastic network，GSN)(Bengio et al，2014)。生成随机网络是去噪自编码器的推广，也可以认为是生成式对抗网络的前言，其除可见变量(通常表示为x)之外，在生成马尔可夫链中还包括潜变量h。

GSN由两个条件概率分布参数化，指定马尔可夫链的一步：

(1)P(x(k)|h(k))指示在给定当前潜在状态下如何产生下一个可见变量。这种 “重建分布”也可以在去噪自编码器、RBM、DBN和DBM中找到[6-10]。

(2)P(h(k)|h(k),x(k-1))指示在给定先前的潜在状态和可见变量下如何更新潜在状态变量。

去噪自编码器和GSN不同于经典的概率模型(有向或无向)，它们自己参数化生成过程而不是通过可见和潜变量的联合分布的数学形式。相反，后者如果存在则隐式地定义为生成马尔可夫链的稳态分布。存在稳态分布的条件是温和的，并且需要与标准MCMC方法相同的条件。这些条件是保证链混合的必要条件，但它们可能被某些过渡分布的选择(例如，如果它们是确定性的)所违反。

1.2 判别性GSN的简介

GSN的原始公式用于无监督学习和观察数据的隐式建模，但研究人员可以修改框架来优化它。例如，Zhou和Troyanskaya以下列方式推广GSN，仅在输出变量上传播重构的对数概率并保持输入变量固定。他们成功应用该方法对序列蛋白的二级结构进行建模，并将(一维)卷积结构引入马尔可夫链的转换算子中[13-16]。重要的是要记住，对于马尔可夫链的每个步骤，需要为每个层生成一个新序列，并且序列计算其他层(例如下一个层和前一个层)的值的输入。因此，马尔可夫链不仅仅是输出变量(与更高的隐藏层相关联)，输入序列仅用于条件化链，其中反向传播使其能够了解输入序列如何条件化由马尔可夫链隐式表示的输出分布。所以这是在结构化输出中使用GSN的一个例子。

Zhrer和Pernkopf引入了一种混合模型，它通过简单地添加(使用不同的权重)受监督和无人监督的费用的总和重建对数概率，将监督目标(例如上面的工作)和无监督目标(例如原始GSN)结合起来。Larochelle和Bengio之前提出了RBM中的这种混合标准，他们证明了该方案下分类性能的提高。

1.3 改进的思路和方式

根据这样的特点，可以对任何一种机器学习方法进行改进。对于生成模型，深度生成模型可以通过从网络中采样来有效生成样本，例如受限玻尔兹曼机(restricted Boltzmann machine，RBM)、深度信念网络(deep belief network，DBN)、深度玻尔兹曼机(deep Boltzmann machine，DBM)和广义除噪自编码器(generalized denoising autoencoders)。很多网络使用的是类似于Sigmoid信念网络的一种深度生成模型，如式(1)所示：

(1)

不过文献中指出问题，生成可见单元的样本在Sigmoid信念网络中是非常高效的，但是在大多数情况下依然不是十分高效。如果对于给定的可见元，这样的Sigmoid信念网络对隐藏单元的推断是非常难解的。因为变分下界涉及对包含整个层的团求期望，均匀场推断也是难以处理的。这个问题一直困难到足以限制有向离散网络的普及[11]。

2 可微模型的设计

2.1 生成模型的设计

生成模型的神经网络由三个部分组成，分别是输入层、隐藏层、输出层，在这里隐藏层设置为4个[19]。大致过程如下：

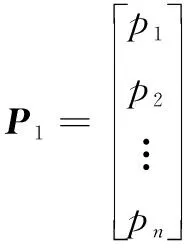
α2=σ2(d(P2))=relu(g(P2))

(2)

(3)建立反卷积层，其卷积核为W4=[5,5,1,64]，偏置量是ω4=[w41]，反卷积层可通过公式z4=dec(a3,W4,str)+b4计算得出。

(4)在输出层使用tanh激活函数激活：

R=tanh(z4)

(3)

生成模型如图2所示。

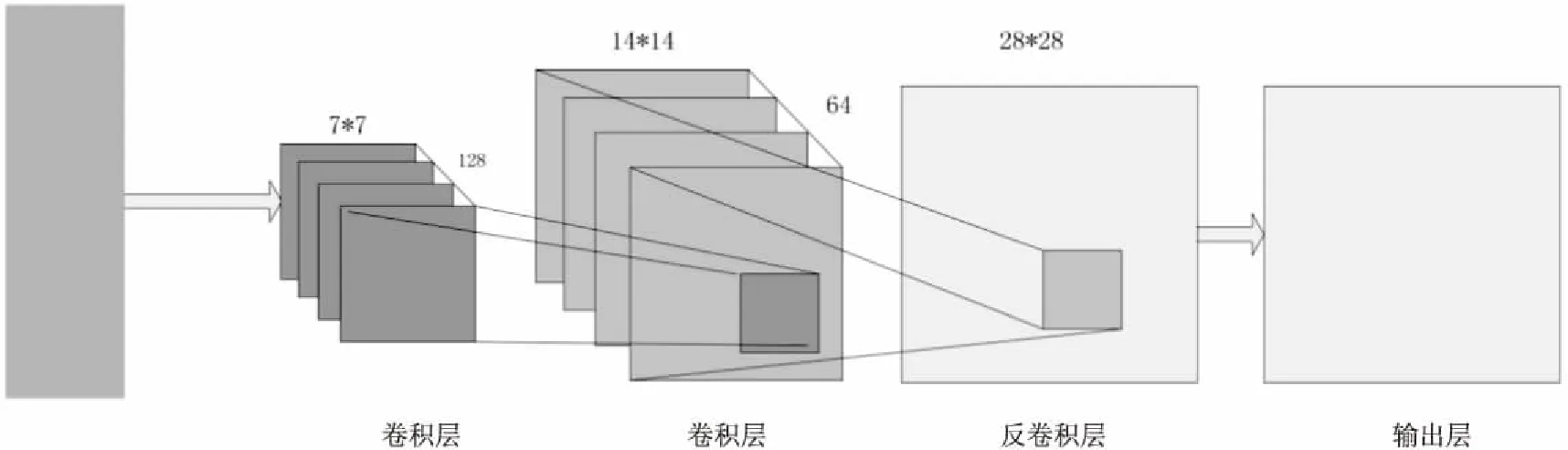
图2 生成模型

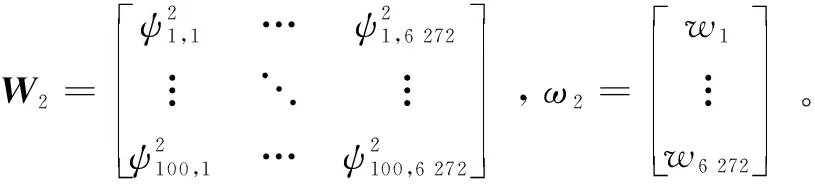
2.2 判别模型的改进

正如DCGAN所示，其增加了正则化、去掉了池化层、各层有特定的激活函数，而激活函数也可根据所需有所改变。

(1)增加正则化，正则化应用到判别模型中，可以大大提高其准确性和训练速度，但不需要将其应用到输出层中，因为如果输出层中也使用了正则化，将会大大影响模型的稳定。

(2)用卷积层代替池化层可以降低采样率，并且，在正则化的影响下，模型的训练速度已经大大提高，所以也没有必要使用池化层了[12-13]。

判别模型如图3所示。

图3 判别模型

3 在MNIST上的数字测试集上样本的平均对数似然性的实验

在MNIST上报告的数字是测试集上样本的平均对数似然性，并且在示例中计算平均值的标准误差[21]。在TFD上，计算了数据集折叠的标准误差，使用每个折叠的验证集选择不同的σ。在TFD上，在每个折叠上交叉验证σ，并计算每个折叠的平均对数似然。对于MNIST，将与其他数据集的实值(而非二进制)版本进行比较。

结果报告在表1中，这种估计可能性的方法具有较高的方差，并且在高维空间中表现不佳，但它是所知的最佳方法。可以采样但不估计可能性的生成模型直接促使了对如何评估这些模型的进一步研究，这是Goodfellow等人[14]使用的方法。

表1 实值版本比较

图4展示了训练后从结果中抽取的样本。虽然没有表示这些样本比现有方法生成的样本更好，但可以这样认为，这些样本至少与文献中更好的生成模型竞争，并突出了对抗框架的潜力。

图4是来自模型中的可视化样本。样品是公平的随机抽取，而不是挑选。与深度生成模型的大多数其他可视化不同，这些图像显示来自模型分布的实际样本，而不是给定隐藏单元样本的条件均值。而且，这些样品是不相关的，因为取样过程不依赖于马尔可夫链混合。

图5、图6是可视化对抗模型的损失率。

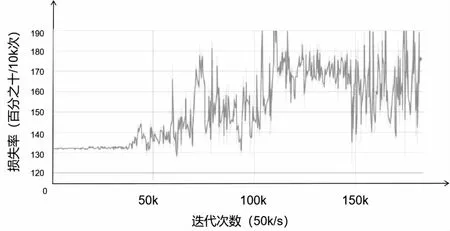
图5 使用Tensorboard可视化的生成模型损失率

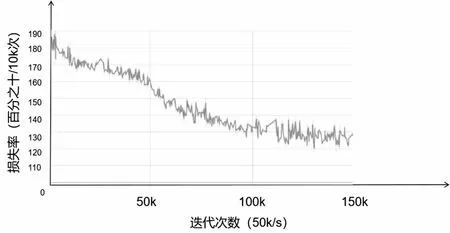
图6 使用Tensorboard可视化的判别模型损失率

4 结束语

在研究中发现，增加正则化，正则化应用到判别模型中，可以大大提高其准确性和训练速度，但不需要将其应用到输出层中，因为如果输出层中也使用了正则化，将会大大影响模型的稳定。用卷积层代替池化层可以降低采样率。这样可以有效地降低损失率，并提高相关的准确性。其次，在生成式模型中，tanh会比sigmoid更常用，在此引入该激活函数。综上所述，改进的无监督对抗生成模型具有较好的效果。