Ni掺杂浓度对CdS:Ni体系电子和光学性质的影响*
2020-04-28郭艳蕊严慧羽宋庆功陈逸飞
郭艳蕊,严慧羽,宋庆功,陈逸飞
(中国民航大学 理学院,天津 300300)
0 引 言
CdS基本晶体结构有4种:(a)纤锌矿结构;(b)闪锌矿结构;(c)岩盐结构;(d)CsCl结构。在一定的实验条件下,这4种晶体结构可以相互转化。纤锌矿结构的CdS空间群是P63MC(编号:186),晶格常数为a=0.414 nm,c=0.671 nm。闪锌矿结构是亚稳态的,在高温环境下可转化为纤锌矿结构,晶格常数a=b=c=0.582 nm,空间群是F43 m(编号:216)。岩盐结构只能在高压条件下存在,晶格参数a=b=c=0.545 nm,空间群为Fm3m。在常温常压下,CdS的稳定结构是纤锌矿结构。因此,本文的研究对象是纤锌矿结构CdS。
CdS是典型的Ⅱ-Ⅵ 族直接带隙n型半导体,在室温下带隙宽度为2.58eV。由于其良好的电学和光学性能,CdS被广泛应用在光探测器、发光二极管、太阳能电池、传感器、光波导器件和非线性集成光学器件等领域,因而备受人们的关注[1-5]。但是,本征的CdS电阻率很大,能达到107~108Ωcm的数量级,这在很大程度上影响了CdS的应用。近年来人们发现,利用其他过渡金属元素或非金属元素掺杂CdS的方法,能有效改善CdS的电学性能和光学性能。比如,Kazume 等[6]发现作为施主型的 S 空位对 Cu 掺杂 CdS 形成 p 型电导起补偿作用;Desnica等[7]研究发现,掺 Cl 等元素可以提高电导率,得到电学性质较理想的n型CdS半导体材料。因此,本文以密度泛函理论的第一性原理作为计算基础,计算并分析了Ni掺杂CdS的能带结构、态密度和光学性质。重点讨论在不同Ni掺杂浓度下,对CdS:Ni体系的影响和作用机理。
1 计算模型及方法
本文以六方纤锌矿结构的CdS为研究对象,α=β=90°,γ=120°。构建模型时采用实验中的晶格常数a=0.414 nm,c=0.671 nm。在本文的计算中,为了研究不同掺杂浓度下CdS能带结构、态密度和光学性质的变化,我们构建了4种不同的超胞,分别是2×2×1结构的16个原子、2×2×2结构的32个原子、2×2×3结构的48个原子、3×3×2结构的72个原子。我们选择用一个Ni原子替换上述4种超晶胞结构中的一个Cd原子,得到的掺杂浓度分别为12.5%、6.25%、4.17%、2.78%,对应的结构图如图1所示。
本文采用超软赝势(Ultrasoft Pseudopotential)[8]来描述离子实与价电子之间的相互作用。选用广义梯度近似GGA(General Gradient Approximation)下的PBE(Perdew-Burke-Ernzerhof)计算方案处理电子与电子间交换相互作用[9]。电子波函数通过平面波基矢组进行扩展,截止能Ecut(Energy cutoff)设为300eV,参与计算的价电子为S: 3s23p4;Cd: 4d105s2;Ni: 3d84s2。采用BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法[10]对晶胞模型进行几何优化,收敛标准为:原子的相互作用力,0.1 eV/nm;单原子能量,0.5×10-5eV/atom;晶体内应力,0.02 GPa;原子的最大位移,5.0×10-5nm。计算程序对4个参数同时进行优化,结构优化完成的标志是4个参数均达到或优于收敛标准。计算工作由CASTEP量子力学模块[11]完成。
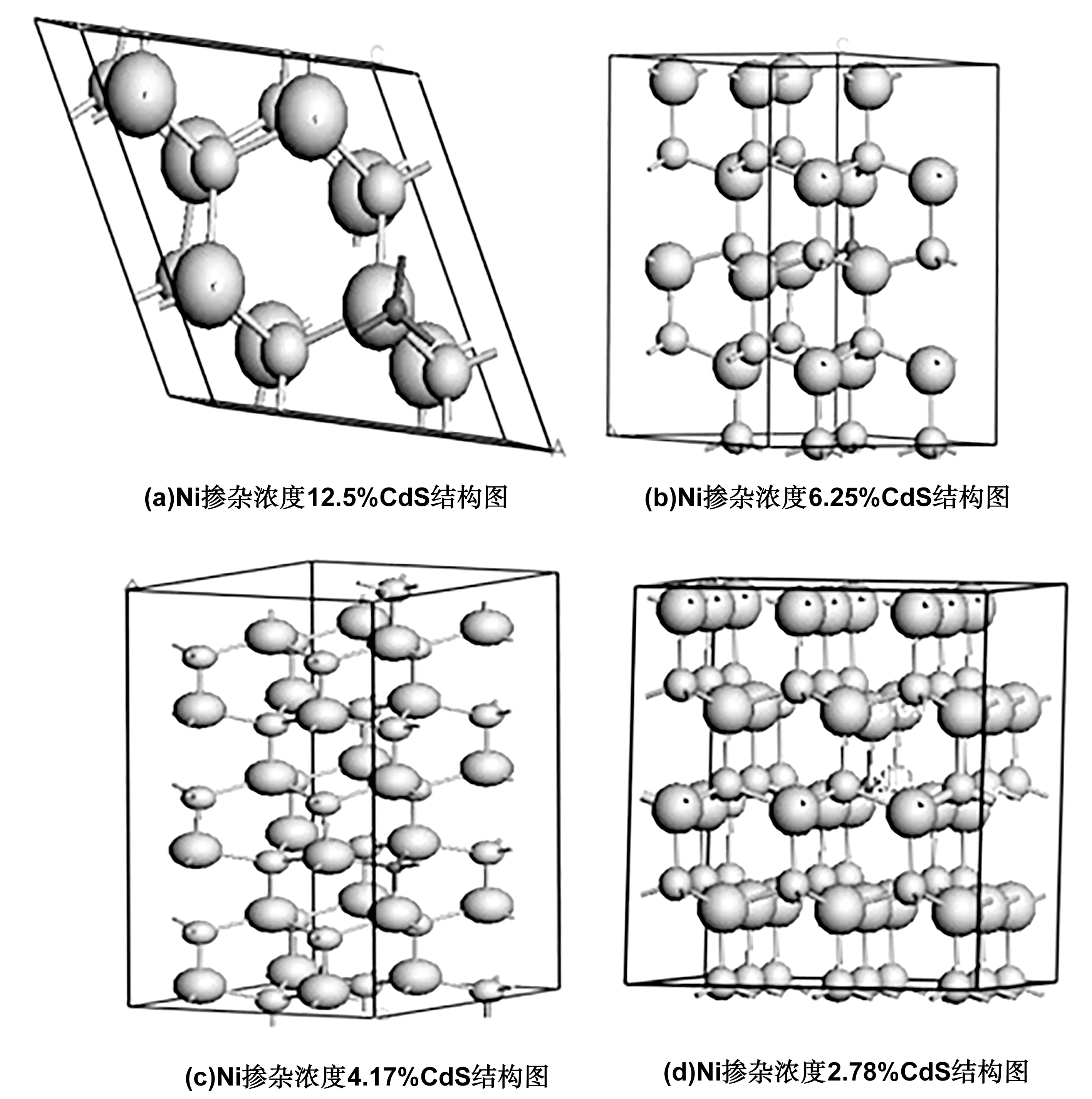
图1 (a)Ni掺杂浓度12.5%CdS结构图;(b)Ni掺杂浓度6.25%CdS结构图;(c)Ni掺杂浓度4.17%CdS结构图;(d)Ni掺杂浓度2.78%CdS结构图(最大原子模型为S原子,次级大的原子模型为Cd原子,最小原子模型为Ni原子)
2 计算结果与讨论
2.1 几何优化结果
我们首先对4个原子的CdS原胞进行几何优化,计算结果给出了晶格常数a和c的值分别为0.423,0.688 nm,与实验值(a=0.414 nm,c=0.671 nm)吻合较好[12]。这表明计算模型和参数设置是合理的。在此基础上,我们对4种不同掺杂浓度的结构分别进行几何优化,得到的晶格常数和元胞体积如表1所示。结果显示,Ni掺入后的晶格常数和晶体积均变小,并且随着掺杂浓度的增加,晶格常数和晶体积均逐渐减小。这主要是因为Ni的离子半径0.073 nm小于Cd的0.095 nm离子半径,导致超胞的晶格常数变小,体积收缩。

表1 不同Ni掺杂浓度CdS:Ni的晶格常数和元胞体积
图2是晶格常数与掺杂浓度的依赖关系。可以看出,计算得到的晶格常数与掺杂浓度间满足线性关系,这与Vegard定律[13]符合得很好。
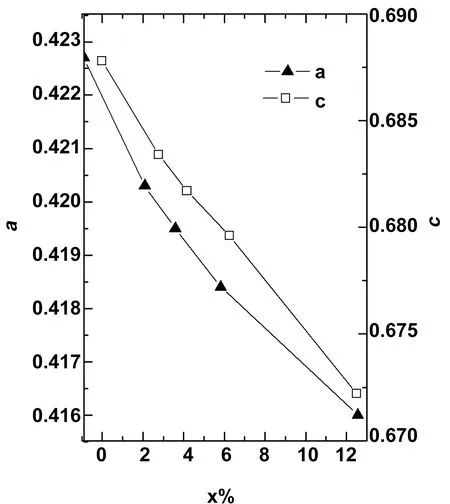
图2 CdS:Ni体系晶格常数a和c随Ni掺杂浓度的变化
2.2 形成能的计算
杂质掺入本征材料中的难易程度以及掺杂系统的稳定性与形成能密切相关。形成能越小,Ni掺杂CdS在实验上越容易实现,相应的结构也越稳定;形成能越大,Ni掺杂CdS在实验上就不太容易实现,结构不稳定。本文的计算中,我们采用在富镉条件下形成能的计算公式:
E=ENi-CdS-ECdS+μCd-μNi
在富硫条件下形成能的计算公式:
E=ENi-CdS-ECdS+μCdS-μNi
其中,ENi-CdS是掺杂系统的总能量,ECdS是本征 CdS 的总能量;μNi和μCd分别是 Ni 和 Cd 原子的化学势。在富镉条件下,镉的化学势μCd可以近似等于块体金属 Cd 中一个 Cd 原子的能量。在富硫条件下,S 的化学势μS等于块体 S 中一个 S 原子的能量,而 Cd 的化学势μCd通过μCd+μS=ECdS关系式得到。我们分别对富镉和富硫条件下一个Ni 掺杂 CdS 的形成能进行了计算,得到不同掺杂浓度Ni掺杂CdS系统的形成能,见表2。
表2 Ni不同掺杂浓度CdS:Ni体系的形成能
Table 2 Formation energy of CdS:Ni system with different Ni concentration

掺杂浓度12.5%6.25%4.17%2.78%原子数目(个)16324872富镉下形成能/eV1.2490.7430.675-0.632富硫下形成能/eV-0.101-0.6068.326-1.981
由以上数据对比分析得出,Ni掺杂CdS无论是在哪种条件下的形成能都较小,这表示掺杂体系在实验上容易实现。其中,在富硫条件下,Ni掺杂浓度为2.78%时形成能最低,CdS结构更稳定。
2.3 能带结构和电子结构的变化
本文计算的纤锌矿CdS和不同浓度Ni掺杂CdS的能带结构如图3所示。从图3(a)可以看出,未掺杂的CdS的价带顶和导带底均在G点上,所以CdS属于直接带隙半导体材料,带隙宽度为1.12 eV。其价带顶接近费米能级附近的曲线呈抛物线型,表示有着良好的电学性质,且导带底部分曲线比价带顶部分的曲线更为分散,说明了没有进行任何掺杂的CdS中的电子有效质量比空穴小很多。我们的计算结果显示,在费米面附近,价带主要来自Cd-4d电子态的贡献,还有少量的S-3p的贡献;导带主要来自Cd-5s电子态的贡献,还有少量的S-3s的贡献。这些计算结果与其他研究成果类似[14-15]。从图3(b)~(e)看出,Ni掺杂的CdS价带顶和导带底均位于布里渊区同一点(G点)处,Ni的引入并没有改变CdS的直接带隙特点。Ni的掺杂都在带隙内引入了杂质能级,且杂质能级与导带分离,有着100%的自旋极化率。电子在跃迁时可先跃迁至杂质带,再由杂质带跃迁至导带,这降低了电子跃迁需要的能量。因此,Ni掺杂后的CdS的导电率与未掺杂相比有了显著地提高。
能带图显示掺杂体系的两种自旋态能带稍有区别,为了深入研究不同掺杂浓度对纤锌矿CdS电学性质的影响,我们分别计算了Ni掺杂浓度为0%、12.5%、6.25%、4.17%和2.78%的掺杂系统的总态密度,见图4。图中将费米能级作为能量零点。图4显示,从整体来看,各种掺杂体系的态密度分布情况比较相似。而与未掺杂CdS的态密度相比,各掺杂体系均在价带顶附近引入了杂质能级,而且,Ni掺杂CdS为浅受主掺杂。结合各体系的能带图和态密度图可以看出,杂质能级均是自旋极化率为100%的杂质能级,因此,Ni掺杂CdS有望成为新型的自旋电子学材料。
为了更加精确的研究Ni掺杂对CdS电学性质的影响,以掺杂浓度为2.78%作为具体分析对象,如图5所示。从图中看出,费米面附近的杂质能带主要来自于Ni-3d电子电子的贡献,而导带的态密度主要来自于S-p和Cd-p电子态。在费米能级附近Ni-d、S-p态和Cd-p态有明显的重叠,表明它们之间存在着较强的p-d杂化,我们认为正是这种p-d杂化导致了费米能级附近的自旋劈裂。
2.4 Ni掺杂对CdS光学性质的影响
介电函数是沟通带间跃迁微观物理过程和电子结构的桥梁,反映了固体能带结构及其各种光谱的信息。Ni掺杂CdS的光学性质可以借助复合介电函数得到:ε(ω)=ε1(ω)+iε2(ω),介电函数虚部ε2(ω)可以直接由多电子波函数计算出来[16]
ε1(ω)为介电函数的实部,是未知的,可以利用Kramers-Kronig方程代入已知的ε2(ω)求解出来。
介电函数虚部能够反映出能级间电子跃迁所产生的光谱机理,更容易和物理过程的微观模型及固体的微观电子结构联系起来。图6给出了不同掺杂浓度CdS:Ni介电函数的虚部。
为了准确反应物质的光学性质,我们运用剪刀算符修正(1.46 eV)来获得与未掺杂实验带隙值(2.58 eV)相一致的结果。考虑到纤锌矿结构的光学各向异性,我们分别分析了入射光方向平行和垂直于晶体方向轴的光学性质。计算结果显示,介电函数的虚部在这两个方向上非常相似,因此在这里我们只讨论010方向的结果。
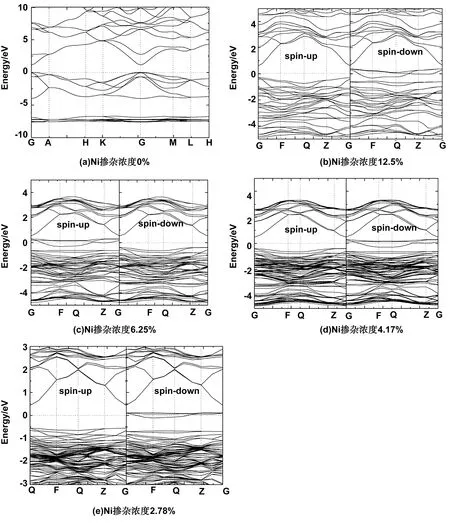
图3 CdS:Ni能带结构图
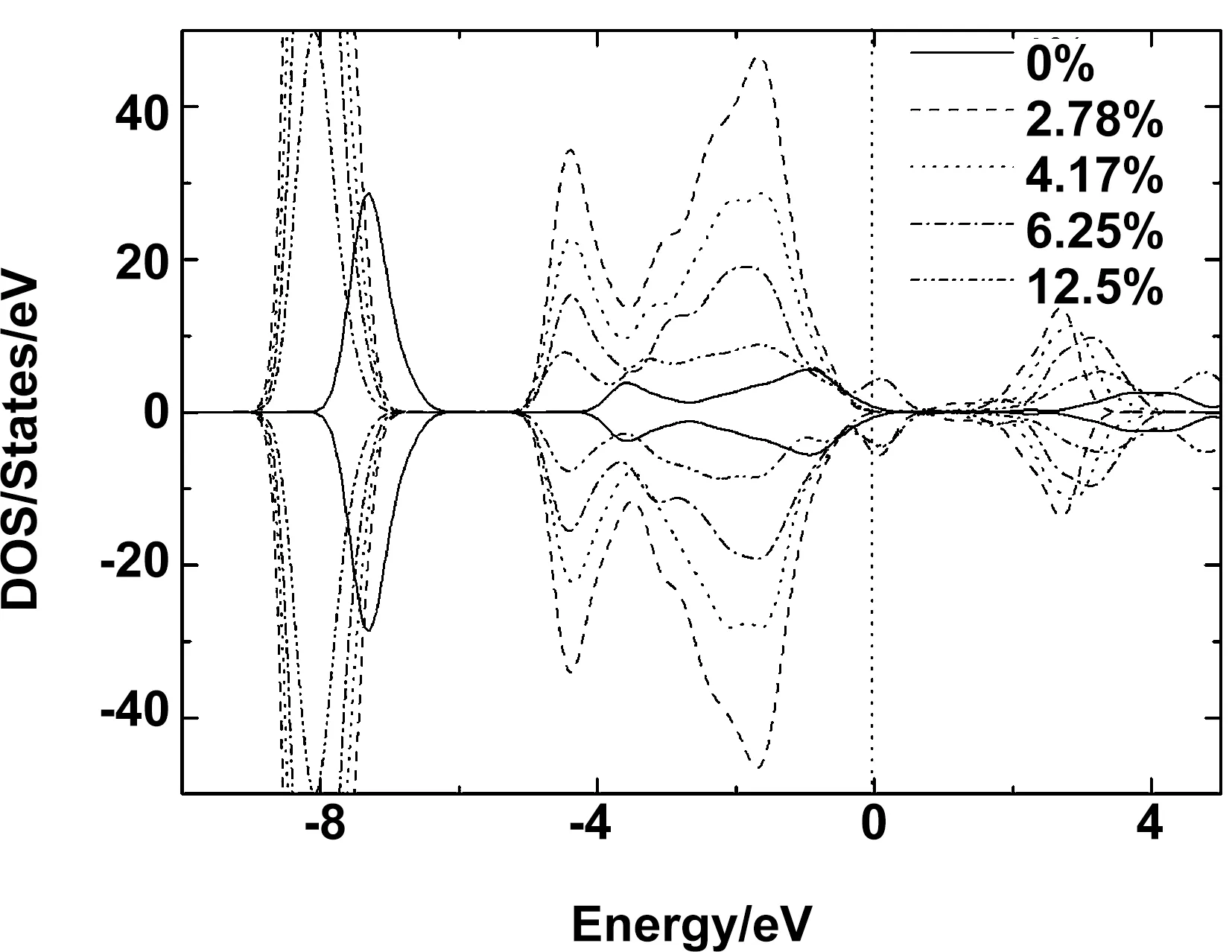
图4 Ni掺杂浓度分别为0%、2.78%、4.17%、6.25%和12.5%的CdS:Ni的总态密度

图5 Ni掺杂浓度2.78%的CdS:Ni的态密度和分波态密度

图6 不同Ni掺杂浓度CdS:Ni的介电函数虚部随能量的变化曲线(010面)
从图6得到,未掺杂的CdS介电函数虚部对应的介电峰主要有D1、D2、D3 3个,它们对应的光子能量分别为3.44、5.52、12.14 eV,这与Huang等人计算结果一致[17]。峰位与能带结构以及电子跃迁直接相关。根据能带结构以及态密度图分析,在D1处的峰对应于价带顶与导带底的直接跃迁,这主要源于S-3p和Cd-5s轨道电子之间的跃迁。D2峰是价带以下能量稍低的能带与导带之间的跃迁形成的,而D3处出现微弱的峰来源于能量最低的能带与导带的跃迁。Ni掺杂之后CdS的介电函数比未掺杂的CdS除了在2.4 eV附近出现了新的主峰外,掺杂体系只出现D2,D3两个峰,峰位几乎和未掺杂的一样。掺杂体系CdS:Ni的介电函数虚部出现的新尖峰,主要是由于价带电子向杂质能级跃迁引起的,使可见光区电子跃迁大大增加。同时原来的D1峰几乎湮灭,原因可能是在未掺杂中D2峰对应的是价带顶到导带底的直接跃迁,Ni的引入,使得费米能级降到价带中,价带顶变为空的,导致价带顶向导带底跃迁的电子减少,进而使D1峰几乎消失。
在得到复合介电函数的基础上,所有宏观的光学性质就可以导出。常见的光学常数吸收系数与复介电函数间的关系如下:
图7给出了不同Ni掺杂浓度CdS的吸收光谱。从图中可以看出,随着掺杂浓度的增加,吸收边发生了红移,这有可能是由于掺杂浓度的增加,杂质能级和价带之间的能隙减小所致,这与之前得到的能带结构结果一致。在2.6~2.7 eV这个位置,原本未掺杂的CdS是没有主峰出现,经过掺杂之后均出现了新的吸收峰,这是Ni原子的掺入对体系引入了杂质能级所致。此外,从图中可以看出,掺杂浓度越大吸收范围也随之增大,吸收能力也进一步增大。综上所述,对于CdS:Ni系统,我们可以通过控制掺杂浓度间接控制半导体材料在可见光区间的吸收峰的位置。
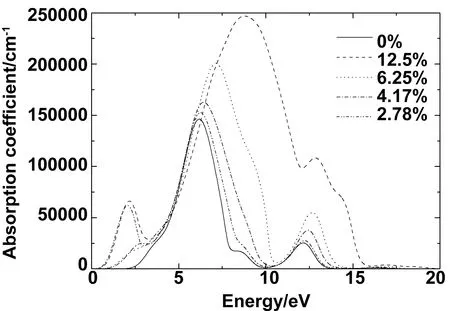
图7 Ni不同掺杂浓度CdS: Ni的吸收光谱(010面)
3 结 论
我们利用基于密度泛函理论的第一性原理计算了本证CdS和不同Ni掺杂浓度下CdS的能带结构、态密度和光学性质。结果显示,无论在富镉还是富硫条件下,计算得到的形成能都比较小,说明了CdS:Ni系统在实验上是容易实现的;CdS:Ni掺杂体系的费米能级附近出现了自旋极化100%的杂质带,提高了材料的导电率;Ni掺杂后CdS系统的光学性质有很大的改变,在吸收光谱上产生了新的吸收峰,并且随着掺杂浓度的增加,吸收范围也会提高。所有结果显示,CdS: Ni半导体有望成为一种新型的透明导电材料。
