螺旋定理在曲柄摇杆机构中的应用研究
2020-04-28阿达依谢尔亚孜旦
陶 赫,阿达依·谢尔亚孜旦
(新疆大学机械工程学院,新疆 乌鲁木齐 830047)
1 引言
机械设备所具有的功能是由其机构所决定的,因此,各国的相关学者从拓扑结构,演化脉络等方面对机构学做了大量的研究工作,促进了机构学从平面向空间,从单自由度向多自由度、从刚性向柔性、从串联向并联的发展与应用[1],使机构学成为现代机械装备的功能、结构设计等方面的依据,同时也成为衡量一个国家装备设计水平和提升国际竞争力的重要基础学科之一。
然而,基于图、文描述的螺旋演化[2]、TRIZ理论[3]、运动副性质改变[4]以及机架变更等机构演化的传统方法促进了机构的发展与应用,但仍有一些方面的不足。如曲柄摇杆机构到曲柄滑块机构演化过程的数学工具的应用使用的相对较少。尽管矢量法、矩阵法等方法对单自由度机构的动力学,运动学特性的分析起到了很大的促进作用,但并没有涉及到演化过程,如四杆机构的演化过程。
近十几年来,螺旋定理的推出促进了柔顺机构,仿生机构等多自由度机构的拓扑结构,动力学分析,运动学特性的研究与运用,显现出螺旋定理在机构学分析的重要性。例如螺旋定理在并联机构2-RPU/UPR研究上的应用[5]。因此,以矩阵的形式并基于螺旋定理探究曲柄摇杆机构向曲柄滑块机构的演化过程。这既为机构演化方面的研究提供了新的探究思路,又可以方便计算机演绎机构演化的过程,还能够让计算机分析机构演化的过程。
2 线矢量的Plücker坐标
机构是由构件通过动联接构成的,构件的长度及其姿态决定机构的空间位置与运动特性。由于机构是用来传递与变换运动和力的可动装置,因此,机构中任何一构件均可视为一有向线段或向量,如图1所示。

其中,P=y1N-z1M;Q=z1L-x1N;R=x1M-y1L
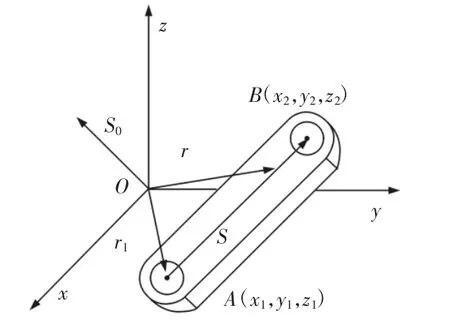
图1 构件的Plücker坐标Fig.1 Plücker Coordinate of Component
根据S与S0的表达式可知,一组满足S≠0且S⊥S0条件的向量S与S0所表达的、可视为有向线段的构件的位置、姿态就被确定。基于线矢量的定义可知,向量S与S0所表达的有向线段为线矢量。此外,以标量λ构成的λS及λS0仍满足线矢量的定义,因而,S与S0是齐次坐标。故线矢量可写成齐次坐标或Plücker坐标$=(S;S0)=(L M N;P Q R)的形式,其中,S 称为 Plücker坐标的原部,而 S0称为 Plücker坐标的对偶部[6]。
因此,线矢量的齐次坐标形式或者Plücker坐标不仅可以描述研究对象的长度和位置,而且还准确地描述研究对象的姿态信息。
3 四杆机构运动副的Plücker坐标
3.1 转动副的Plücker坐标
一平面四杆机构,如图2所示。由于具有平面特性,因此,为建立Plücker坐标,可以在平面四杆机构所处的平面的法线方向任意拉伸。为研究方便,取Z轴为平面的法线,并在该方向取拉伸的长度为单位1,即杆件在Z轴方向的宽度皆为1。因此,可得到各转动副线矢量的模长皆为1,由于所以,转动副线矢的 Plücker坐标的原部皆为(0,0,1)。

结合图2中的几何关系以及式(1)和式(2)可知,利用矢量和矢量的叉乘关系,即可求得转动副线矢量的 Plücker坐标对偶部为 S0=(asinθ1-acosθ10),其中:
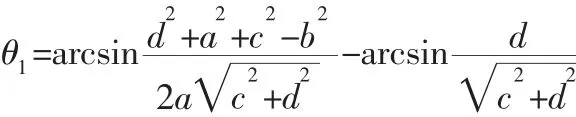

图2 曲柄摇杆机构Fig.2 Crank-Rocker Mechanism
基于上述分析,可得转动副B的Plücker坐标表达式为$B=(0 0 1;asinθ1-acosθ10)
同理可以求出转动副A,C,D的Plücker坐标表达式:$A=(0 0 1;0 0 0),$C=(0 0 1;c-d 0),$D=(0 0 1;0-d,0)
3.2 移动副的Plücker坐标
移动副的运动特点是直线运动,而直线运动可以视为是圆周运动的特例,即半径r趋向于∞的运动轨迹。由于构成运动副的构件可视为刚体,所以,可以把刚体作为研究对象,如图3所示。因此,可以由转动副的 Plücker坐标或(ω;r×ω)[7]推导出移动副的Plücker坐标。刚体处于初始t=0时刻的状态,如图3(a)所示。刚体质心与转轴的距离 r=r0,r0∈(0,∞);与此同时,r与水平线的夹角为 α,α∈(0,2π);初始角速度为 α/t0,t0大于 0。图 3(b)描绘了处于平面复合运动状态下的刚体,假设刚体的线速度大小为v,刚体质心与转轴中心的距离r以m的速度在增加。随着时间的推移,当r→∞时没有实际意义,因此,若使刚体或移动副的线速
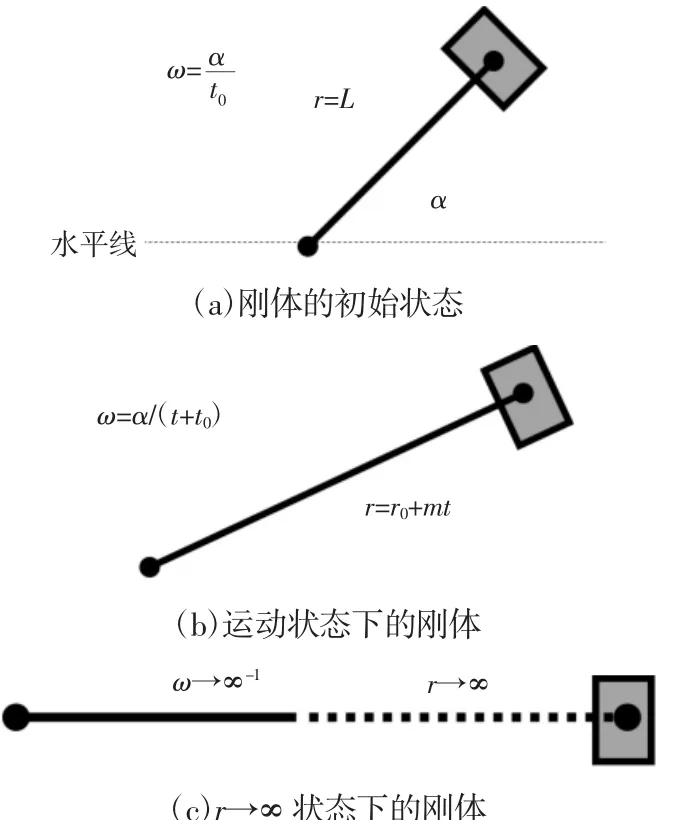
图3 刚体的运动演化过程Fig.3 Process of Evolution About the Movement of Rigid Body
因此,当ω=α/(t+t0)时,随着时间的推移,ω→∞-1且r-1与ω满足同阶无穷小,则刚体的线速度为:
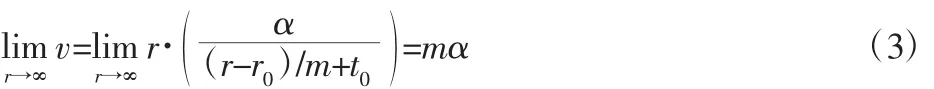
由式(3)可知,当 r→∞,如图 3(c)所示。刚体的运动轨迹必然趋于直线,与此同时,由于r-1与ω满足同阶无穷小,因此,刚体的线速度v趋向于一个稳定值mα,其次,式(3)同时也描述了刚体由圆周运动转变为直线运动的过程,即:相对于观察者的无穷远处的刚体运动表面上处于静止状态。但静止是相对的,运动是永恒的。因此,移动副或刚体直线运动的Plücker坐标的表达式为偶量 $=(0;v)=(0;S0)。
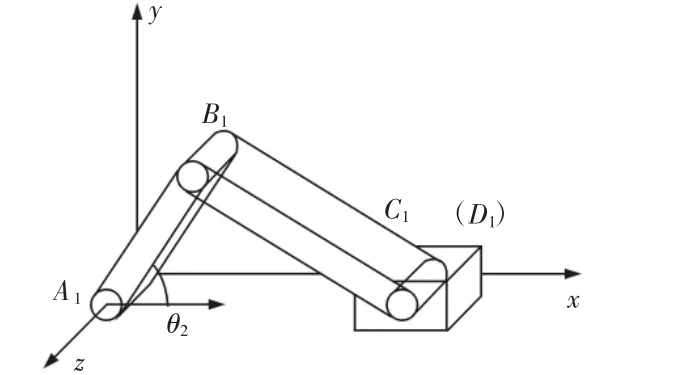
图4 曲柄滑块机构Fig.4 Crank-Slider Mechanism
3.3 基于矩阵运算的转动副到移动副转化的表达式
当Plücker坐标系Axyz变换到Oxyz时,如图5所示。则线矢量到线矢量的位置变换可以用下面的矩阵式进行描
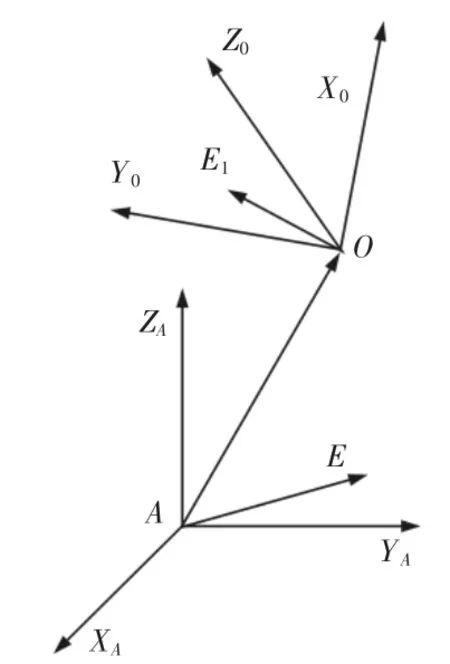
图5 Plücker坐标系的映射Fig.5 Mapping ofPlücker Coordinate System
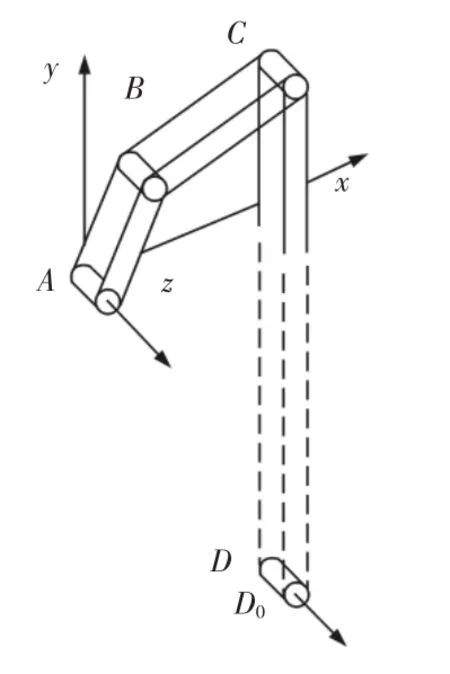
图6 四杆机构的演化过程Fig.6 Process of Evolution About Four-Bar Mechanism
其中,对偶矩阵T[9]$为:

T$表述了Plücker坐标系的一般变换中的旋转,平移等。在T$中,]表示坐标系Axyz对于Oxyz的方向余弦矩阵;而矩阵表示O点相对于A点在x轴、y轴、z轴方向上平移的量分别为OAx、OAy、OAz。即:

因此,可运用式(4)描述四杆机构中的转动副$D=(0 0 1;0-d 0)到移动副的演变过程。
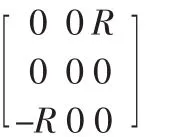
为方便计算,假设CD杆延长的长度以d/t0的速度在增加,因此,R=-d·t/t0。在CD杆在变长的同时,CD杆在Z轴方向的厚度以函数L=t0/(t+t0)的比例在变小。基于上述分析,曲柄摇杆机构到曲柄滑块机构演化过程的矩阵表达式为:
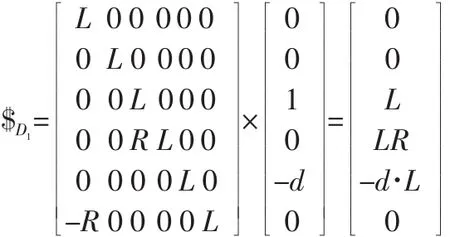
由于时间的推移,R→-∞,因此:
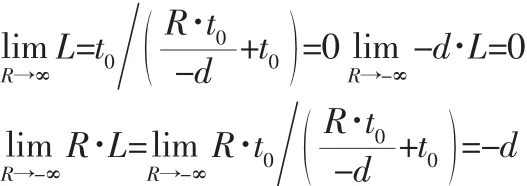
因此,$D1=(0 0 0;-d 0 0)
4 应用实例

当构件 CD 在变小的同时,由于$B=(0 0 1;asinθ1-acosθ10)在x轴,y轴方向上所经过的位移的分量分别为acosθ2-acosθ1,asinθ2-asinθ1,因此,结合式(5)可知,可运用矩阵关系式$B1=T2$B来刻画其演化过程,因而,矩阵T2为:
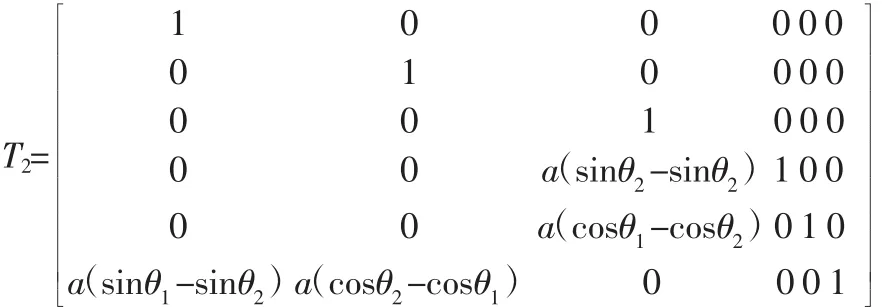
根据图4的三角形ΔA1B1C1的几何关系可以求得:
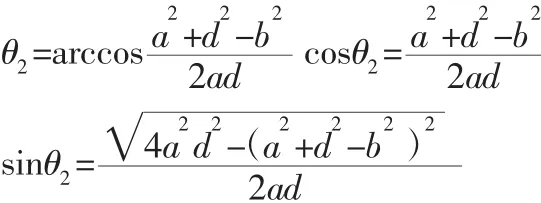
5 结论
(1)基于螺旋定理建立了四杆机构转动副与移动副的Plücker坐标,并在此基础上利用螺旋定理探讨曲柄摇杆机构到曲柄滑块机构的演化过程,得出其演化过程的矩阵表达式。这既显示出螺旋定理涵盖矢量法并兼具矩阵法的优点,又揭示了转动副与移动副的内在联系,同时,也为机构演化的研究开辟了新的途径。(2)曲柄摇杆机构到曲柄滑块机构定量演化的数学方法可能不止存在这一种形式,因此,其它描述其演化途径的数学方法有待进一步的研究。
